相机与相机模型(针孔/鱼眼/全景相机)
0. 摘要
本文旨在较为直观地介绍相机成像背后的数学模型,主要的章节组织如下:
-
第1章用最简单的针孔投影模型为例讲解一个三维点是如何映射到图像中的一个像素
-
第2章介绍除了针孔投影模型外其他一些经典投影模型,旨在让读者建立不同投影模型之间的建模过程
-
第3章介绍如何把不同的投影模型用一个统一的投影过程表达
-
第4章进一步补充第三章的统一投影模型,并介绍畸变的定义和去畸变的原理
-
第5章针对全景相机的基本概念和两种应用广泛的全景相机模型做出介绍
-
第5章用代码示例介绍如何使用OpenCV的接口对图像去畸变
1. 相机成像过程
为了具体说明相机的成像,可以以最简单的针孔相机成像来予以说明。
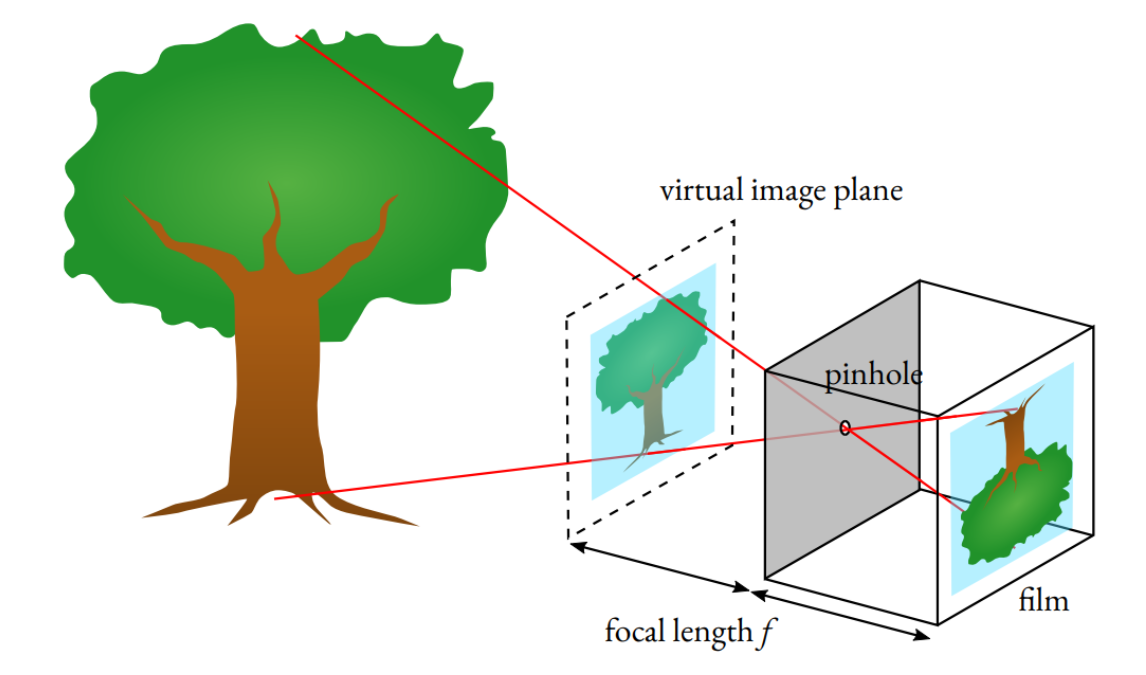
针孔相机由一面有小光圈的遮光盒和另一面有胶卷组成
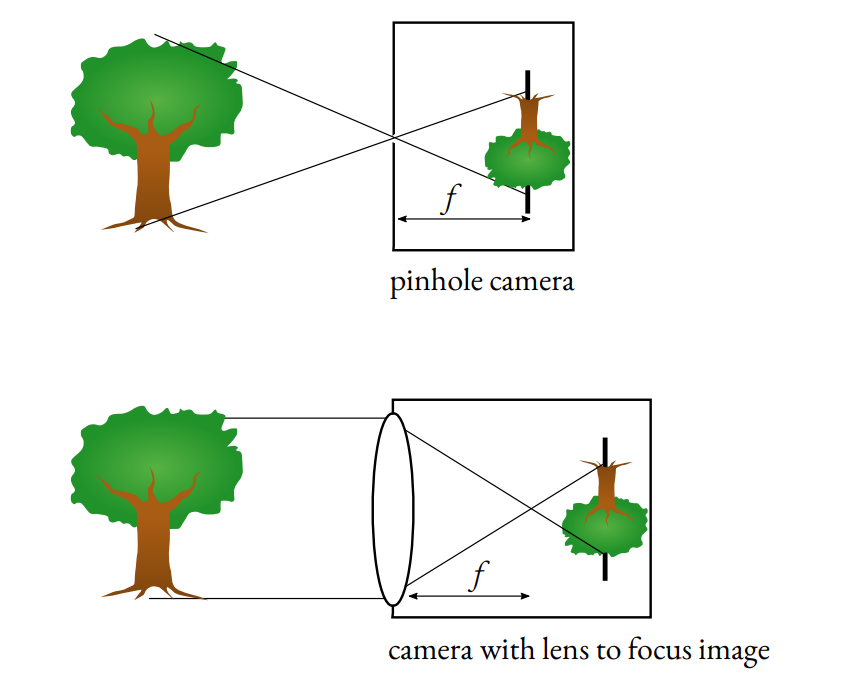
由于研究中使用的大多数商用相机都是基于类似的结构,使用薄透镜、小孔径和光传感器代替胶片,因此在计算机图形学和计算机视觉研究中,针孔相机模型通常用于解释和建模图像形成。
说到图像的成像,就必须提到三个坐标系,相机坐标系、世界坐标系、图像坐标系
a)ICS:图像坐标系是附着在每个图像上的坐标系,用于指定像素位置。按照惯例,从观众的角
度来看,原点位于图像的左上角,x-指向右侧的轴,以及y-轴向下。
b) CCS:摄影机坐标系的原点附着到摄影机,计算机视觉约定使用带z的右手系统,那么z-指向相
机正在观察的对象的轴(指向相机的外侧和图像平面的内侧),y-指向下方的轴,x-轴向 右。
需要注意,OpenCV使用的这种约定可能与计算机图形软件(如Blender)中使用的视图坐标系不同,后者使相机观察方向未负z坐标和y-指向上方的轴。
c)WCS:世界坐标系将摄影机与场景中的其他对象相关联。

一个三维空间中的点怎样映射到图片上的一个像素?
先从一个最简单的问题开始:一个三维空间中的点是如何经过相机成像变为图像上的一个像素的?
我们最常见的投影模型Perspective Projection Model 描述的就是针孔相机 的成像原理。从上面的图根据相似三角形可以得出:

其中为光轴在图像中的坐标,如果相机的光轴与感光元器件完全对齐的话,
,
是图像的宽度(单位是像素)。
从上面的关系可以得出,将一个三维点投影到像素坐标系的时候,可以直接使用下面的公式。对应的就是针孔相机模型。下标 表示这个点是在相机坐标系下的点
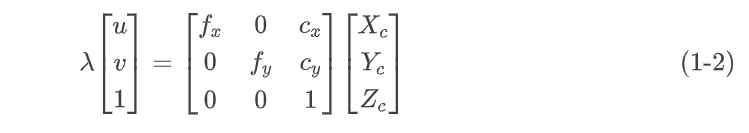
公式(1-2)在代码中也经常对分开进行计算
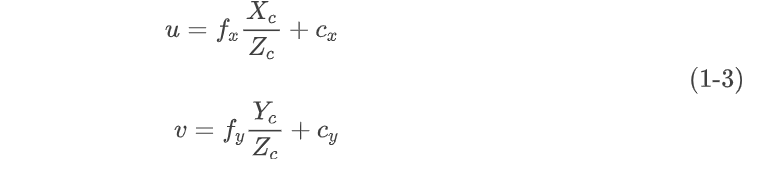
当然,为了简化记号,公式(1-2)也通常记为矩阵相乘的形式:

如果我们提前对做归一化处理,也就是除以
(假设点位于相机前,即
),则可以去掉
系数,即如下形式:

公式(1-4)中位于
的平面,又叫归一化平面(nomalized plane),下文会再次提到。
公式(1-2)到公式(1-5)其实都是等价的.
如果给的三维点是在世界坐标系下,也就是,那么我们只需要先把该点用相机的外参转换到相机坐标系下(刚性变换)即可:

由于刚性变换过程不影响对相机投影模型的讨论,因此后面都假设三维点是处于相机坐标系
相机坐标系
在OpenCV中及大部分视觉处理库中,相机坐标系的规定都与上述的图一致,就是相机光轴往前为,图像水平往右为
,图像垂直往下为
。不过要注意的是在一些仿真渲染器或者特定任务的数据集中可能会规定图像垂直往上为
,前为
,朝左为
,但是这一点是无关紧要的,这一点差别可以反映在相机的外参里,也就是公式(1-6)中的
,只要按照OpenCV的方式规定相机坐标系,总是可以找到一个外参矩阵
将世界坐标系下的点变换到相机坐标系(前
右
下
)。
小结
问:相机是如何成像的?答:光束从物体表面反射,经过相机镜头,到达感光原件,这一系列物理过程可以通过数学公式表达,最终变成一个简单的矩阵操作将三维空间中的点映射到图片的一个像素。具体来说,流程图如下:
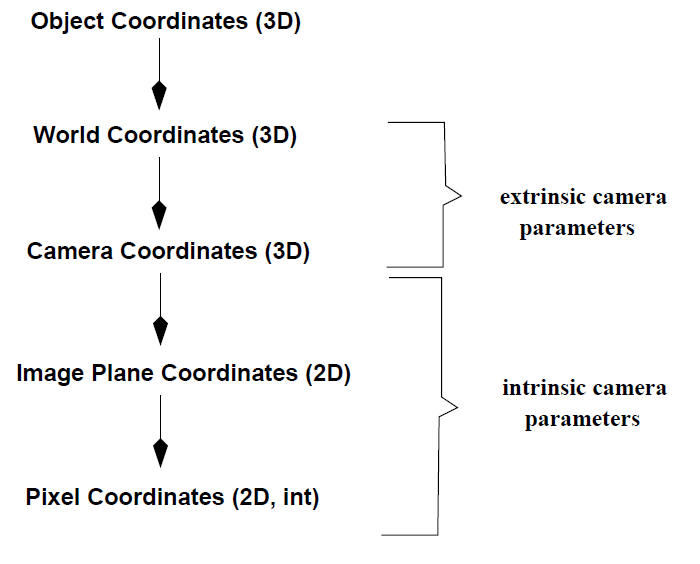
一般来说,世界坐标系和像素坐标系通过一组物理坐标系相关联参数,具体如下:
* the focal length of the lens 透镜的焦距
* the size of the pixels 像素大小
* the position of the principal point 主点位置
* the position and orientation of the camera 相机的位置与姿态
2. 不同的相机投影模型
第一节介绍的是针孔投影模型,但是事实上相机镜头都是多种多样的,不可能都是符合针孔投影模型。本节会介绍经典的相机投影模型,并从直观感受和形式化定义上介绍不同的投影模型是如何联系在一起的
什么是相机投影模型
相机投影模型用数学的方式描述了一个真实世界中的三维点到图像上像素坐标的映射关系
相机投影模型实际上就是对相机成像过程(物理)的数学建模。建模的目的是为了能够尽量符合真实的成像过程。不同的建模方式就对应不同的相机投影模型
经典的相机投影模型
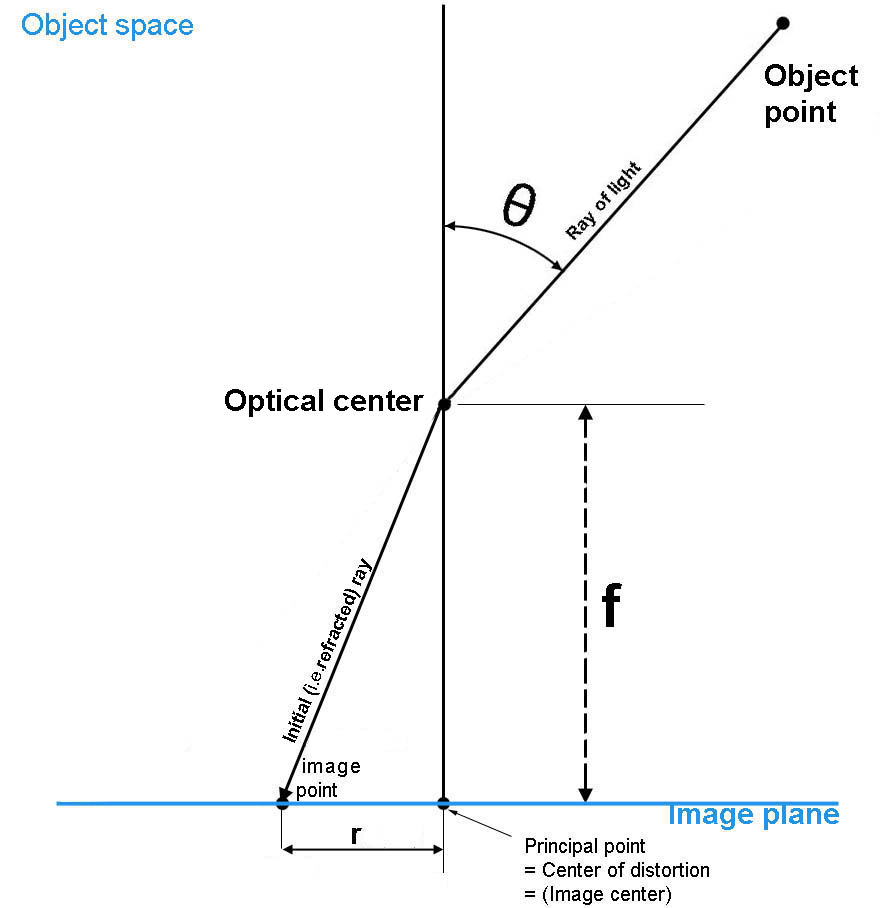
我们回头看看公式(1-3),并暂时只关注轴的映射关系:

上式中称为相机焦距,反应了一个单位长度应该映射为几个像素,单位是,
是相机坐标系(以光轴点为原点)到图像坐标系(以左上角为原点),这两个参数都是相机的固有参数。而上式轴
刚好是点
到相机光心连线与光轴角度的正切值,我们记光束与光轴的夹角为
,并将图片原点移动到图片中心,则公式(1-3)可以写为:

上式的示意图如下(图中的在只考虑
轴的时候就是
):
在公式(2-1)中,轴的投影坐标是
的函数,于是,我们是否可以用不同的函数表达这个过程?答案是肯定的!不同的函数就对应了不同的投影模型。下图就给出了在经典投影模型中对
的不同映射方式。
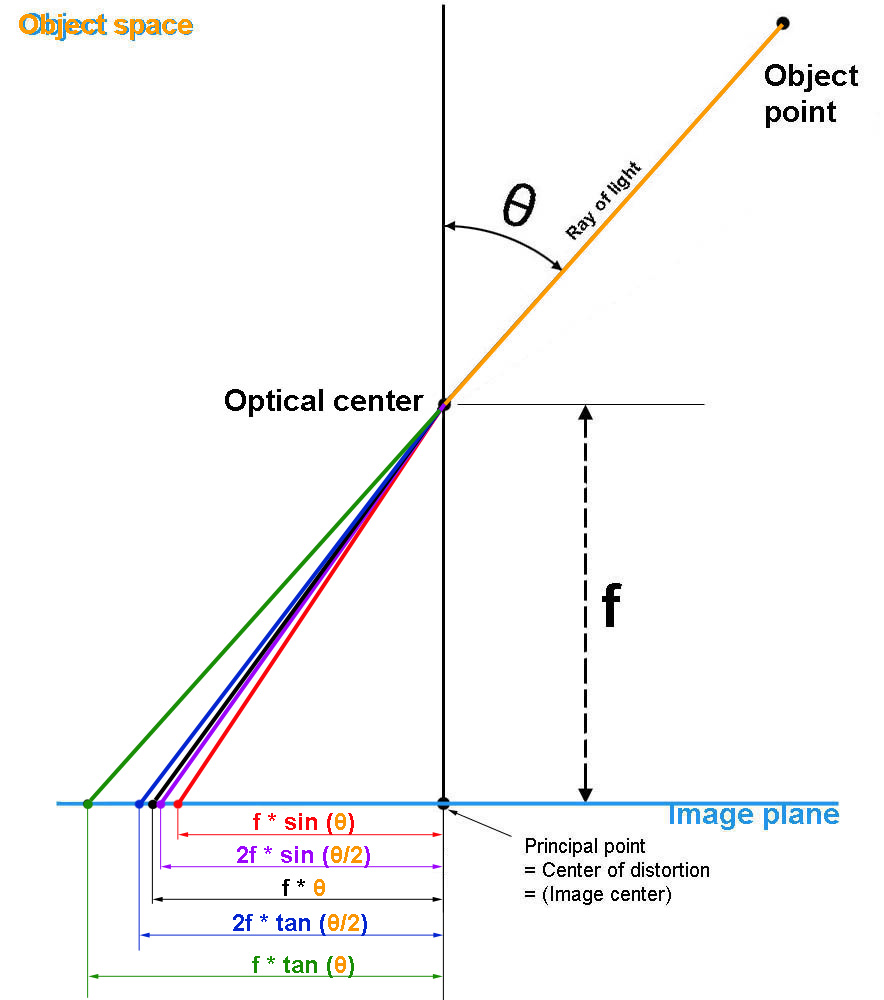
事实上,作为相机的焦距,在上图中的不同投影模型都统一出现,于是我们可以舍弃焦距符号。于是,上图中不同的函数关系与投影模型的对应关系如下:

上面两幅图出自:Models for the various classical lens projections,这篇文章比较形象地介绍各种经典的相机投影模型,并给出他们的函数曲线分析。不过总体偏形象化,没有引入更形式化的描述。
3. 相机投影模型的统一表达形式
上一节我们将投影关系限制在轴,并且给出了较为直观的图示。目的在于两个:1)给读者建立更深刻的相机投影过程;2)让读者对几种经典的投影模型有初步的直观了解。在这一小节中,我们给出更为统一的相机投影表达方式,同时为后文讨论相机的畸变 建立必要的理论基础。
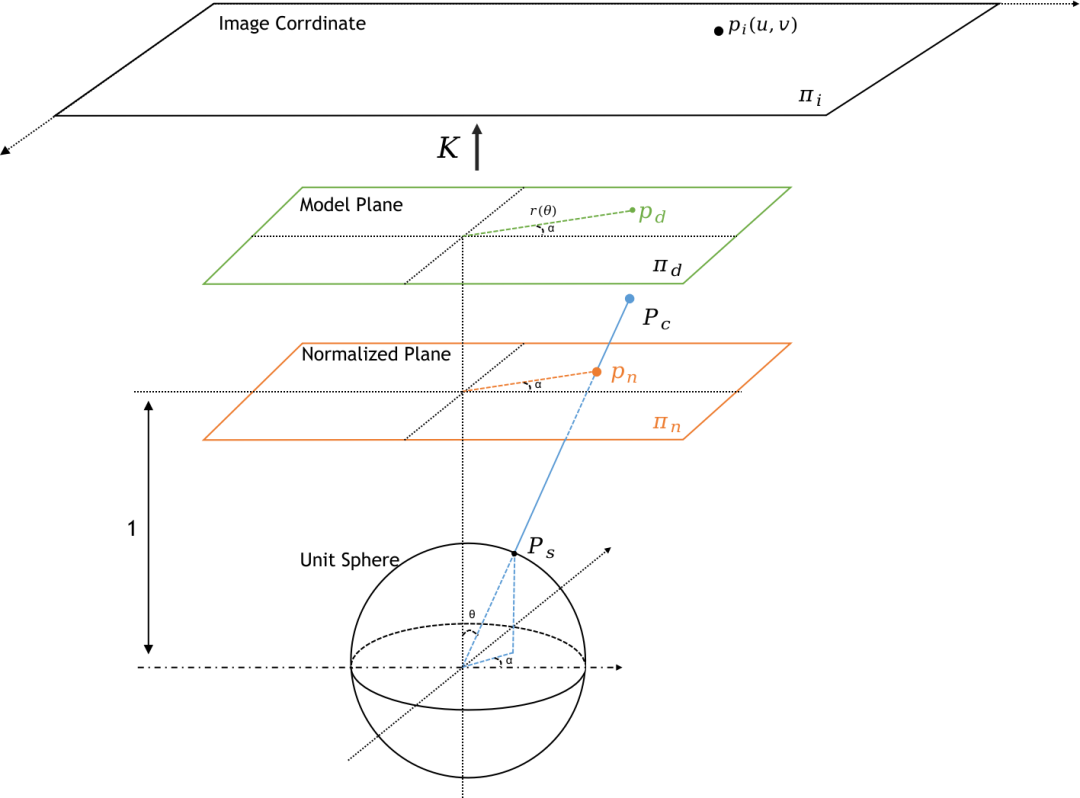
我们将相机的投影过程拆分为三个过程:1)将空间中的点投影到单位球表面;2)将单位球上的点投影到归一化平面;3)将归一化平面上的点利用针孔模型投影到图像坐标系。下面详细介绍这几个过程
单位球投影
想象一下一束光束从相机光心射出,经过图像中的一个像素然后往外无限延伸,可以想象到,这个光束经过的任何点到图像的投影都是经过的那个像素。这个简单的事实告诉我们,我们可以对一个三维点进行任意的放缩,其在图像上的成像点都不会改变。于是,我们将三维点除以它自身的膜长,将其投影到一个单位球,其投影坐标
为:

示意图如下:
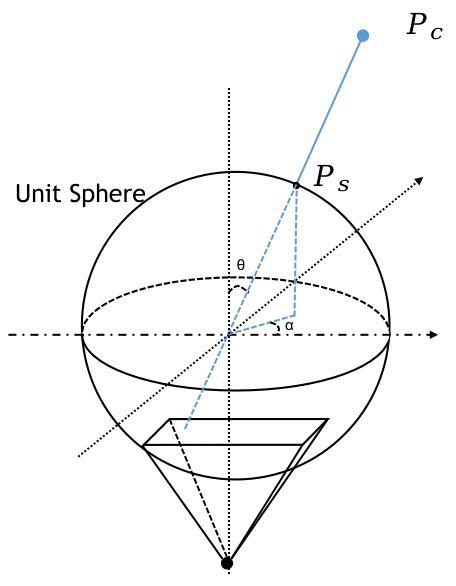
在上图中, 是光束与光轴的夹角,
为光束与水平轴的夹角。
两个角度有如下关系:
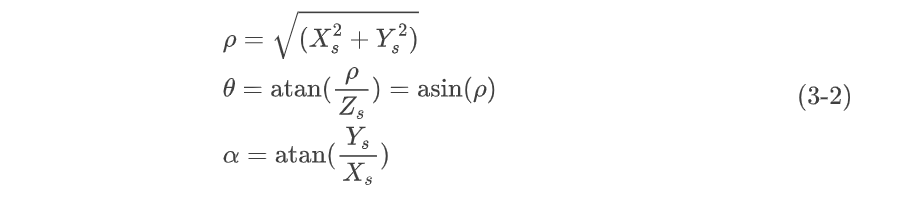
之所以构建 和
是因为我们后续可以将投影过程建立为这两个角度的函数,也就是只与光束的角度有关,而与具体的点坐标无关,这也是符合直观的。
另外,从前面的叙述以及常识,我们知道针孔成像结果是一个倒立的像,为了方便叙述,我们可以将相机做一个镜像,如下图所示:
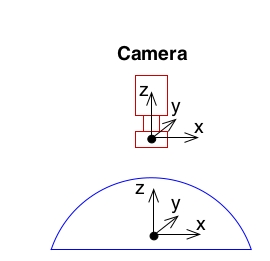
这个单位球有时候又叫视球(Viewing Sphere)。
归一化平面与模型平面
将世界坐标系的点投影到单位球后,我们进一步将其映射到 的平面上,这个平面又叫归一化平面(Normalized Plane)。此时不同的投影模型会对在归一化平面上的点到原点的连线做放缩
,为了后文叙述的统一性,我们再拆分出一个模型平面。在归一化平面上的点只是与
光心点的连线和平面的交点,即:

在模型平面上(Model Plane),对归一化平面上的点做半径放缩,即:

这两个平面的变换过程如下图所示
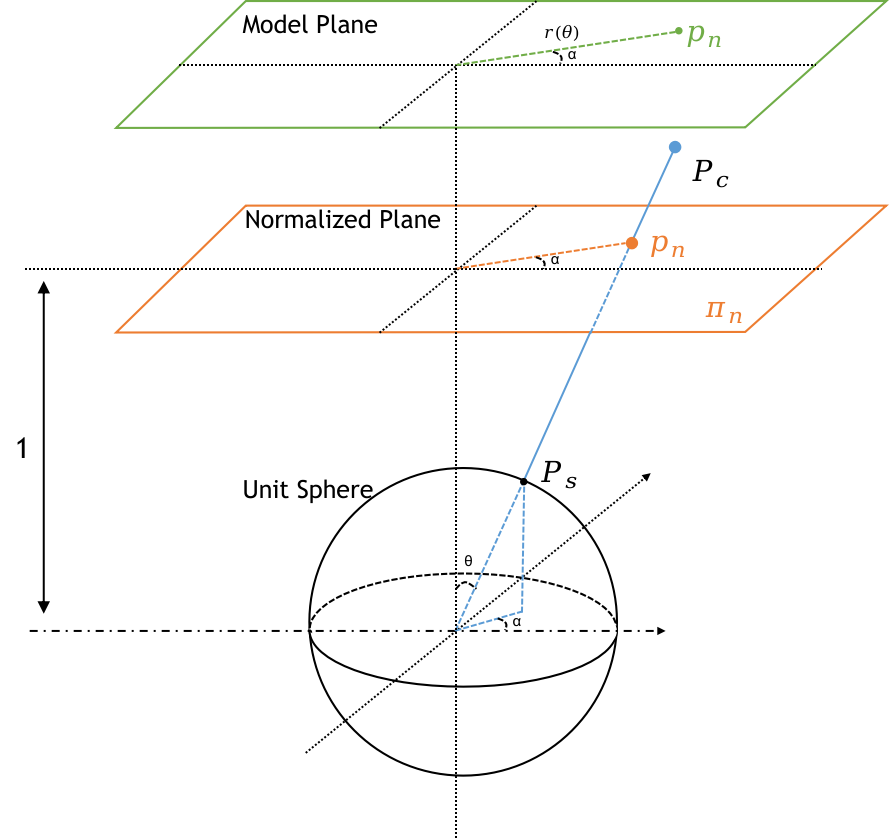
从第二节中经典的投影模型我们发现,其实不同的投影模型都没有对产生影响,而是对投影点到原点的距离
建立不同的函数形式。
稍后将看到,为了能将所有模型都统一为针孔投影模型,会将模型平面变为畸变平面,用更具一般性的多项式代替前面的表达形式。(因此,现在模型平面上的点用下标标明,表示distortion)。
透视变换
得到模型平面上的坐标后,我们可以用相机内参将其变换到图像平面,这个步骤实际上就只是坐标的变换了。
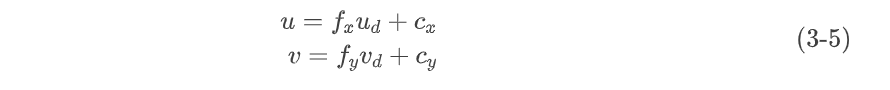
最后,我们可以得到一张完整地表达相机投影模型的示意图:
将针孔投影带入上述统一模型
我们可以将针孔模型,即代入上面的模型,联立公式(3-1)-(3-5),最后可以发现,公式(3-5)的结果其实就是公式(1-3),也就是针孔投影模型的公式。这个过程比较简单,就不再展开公式。读者自己推导一下这个过程非常有利于理解上述的过程。
不同投影模型的函数图
我们可以将不同的经典投影模型的函数画出来(横轴为 ,纵轴为
),结果如下:
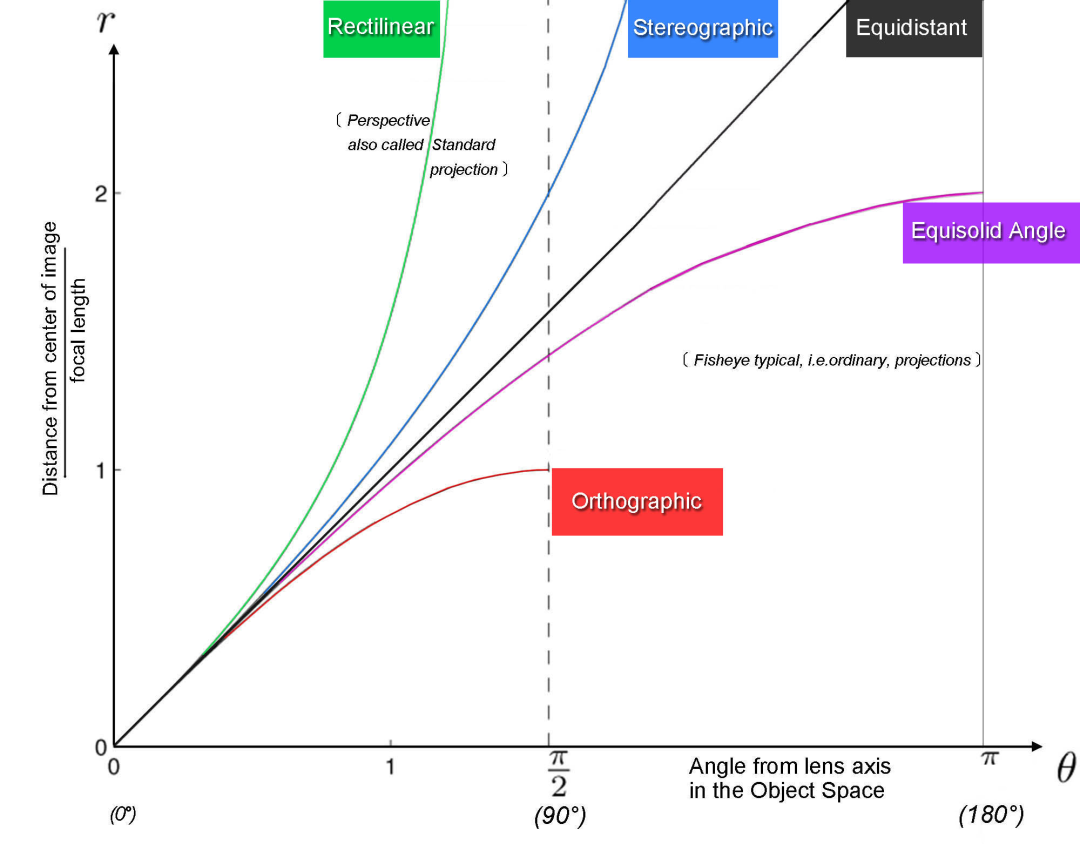
从上图我们应该至少要观察到一个重要的事实:针孔投影模型无法对的视野成像。因为
在90度的时候会趋于无穷大。实际上,从上面的函数图可以看到,针孔投影模型只能在大约水平140度以内的视野成像。
相机投影模型总结
到目前位置,我们应该建立至少以下几个方面的认识:
-
统一化的投影模型经过:单位球投影->归一化平面->透视变换几个过程,将一个三维点投影到图像上的像素
-
不同的经典投影模型在投影过程中不会改变光束与轴的夹角,只是对像素到图像原点的距离建立不同的方程
4. 相机的畸变
针孔模型的优越性
首先描述一下我们人类直观上对于“标准的图像”这个词的一个感性认识,是不是我们会觉得横平竖直,真实中是直线则图像中也是直线,这样的图片会比较“标准”?事实上,针孔投影模型就刚好具有这样的性质。这个性质也可以从其投影方程看出来。经过针孔成像的物体,好像就是把整个物体缩小放在图片上,因此圆是圆,直线是直线。而其他投影模型就可能会呈现膨胀、紧缩的成像效果。如下图所示:

定义
“畸变”这个词从词语上应该理解成由于镜头加工等因素造成镜头与投影模型的差异。但实际上,相机畸变现在描述的是相机成像过程与针孔投影模型的差异(a deviation from the pinhole model) ,也就是:针孔投影+畸变模型=实际成像
而“去畸变”则是使用畸变模型对图像进行逆操作,使得图像就像用针孔投影模型成像出来的一样。
在归一化平面插入畸变模型
为了能够利用针孔模型的性质,我们在前文给出的统一相机投影模型中将模型平面用畸变平面代替。这里的核心思想是,用一个更具一般性的多项式替代各个投影模型中的模型函数,以此达到用一个方程表达多个投影模型的目的。
替换后的示意图如图所示:
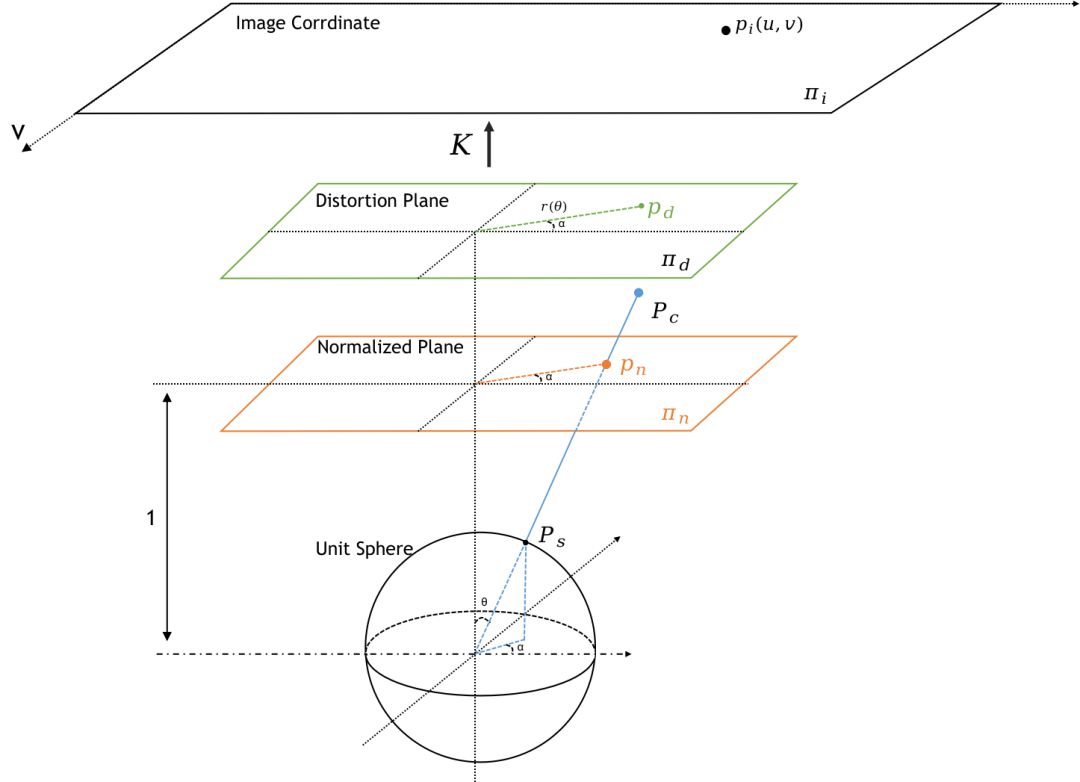
注意上图与上一节最后的统一投影模型其实是一样的,不过Model Plane名字换成Distortion Plane
我们这一节采用OpenCV实现的畸变模型来讲解畸变过程
我们还是先将点投影到归一化平面得到
,并令其到原点的半径为:
径向畸变(Radial Distortion)
所谓的径向畸变(Radial Distortion)就是指只对点做半径上的伸缩变化,这一点其实就跟经典投影模型一样用一个函数建立半径的变化,在OpenCV中,标准镜头的径向畸变可以用如下方程表达:
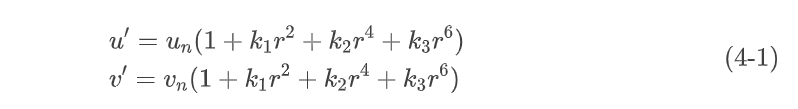
径向畸变对于环绕光轴一周的改变是一致的,因此也叫做半径对称畸变(Radial Symmetric Distortion)或者畸变的对称部分(Symmetric Part Of Distortion Model)
切向畸变(Tangential Distortion)
真实的镜头由于加工误差和安装误差,会导致镜头与感光原件的中心不是完全对齐的,因此在平行的方向上会与标准的针孔成像模型有差异,这种差异对于光轴不是旋转对称的,也叫做切向畸变(Tangential Distortion)
OpenCV中镜头的切向畸变方程如下:
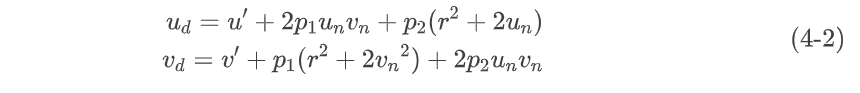
公式(4-1)和公式(4-2)中的叫做畸变参数(Distortion Coefficients)。
去畸变
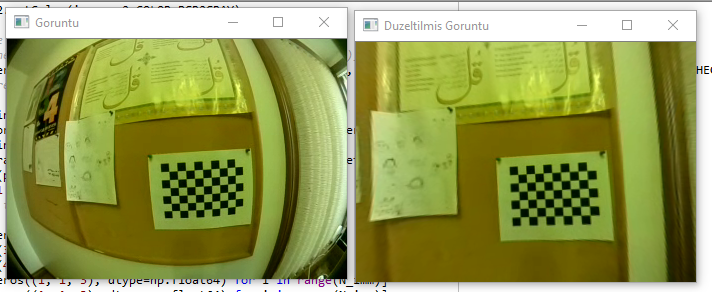
有了畸变模型之后,我们就可以将一个三维点经过:单位球投影->归一化平面投影->畸变模型->透视变换,得到该点在图像中的像素位置。我们可以通过一些标定物,经过求解得到上述的畸变系数,进而得到畸变过程的反过程。我们将图像上的点先经过透视变换的反变换得到在畸变平面上的点,再经过畸变过程的反过程,再投回图像中,这样我们就得到一副没有畸变的图像,其看起来就像是用完全标准的针孔投影模型成像的照片。
下面的图片展示了从畸变到去畸变的图像变化
做完去畸变后,整个的成像过程就像直接用针孔投影模型(公式1-3)成像一般,就像下图一样。
提出畸变模型的文章需要给出如何标定出畸变参数,同时如何计算从畸变点到非畸变点,这里面主要是一些数学求解,这里就不展开讨论,有兴趣的可以看看wiki:Distortion
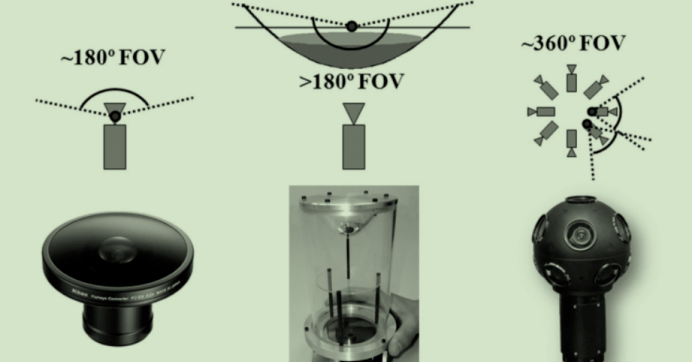
5. 全景相机(Omidirectional Camera)
所谓的全景相机广泛概念上指成像角度能够大于等于180度的相机,他们看起来大概像是下面这样
从第二节(不同的相机投影模型)我们可以知道,根据针孔投影模型设计出的镜头无法对大于等于90度(左右)的视野成像,通常由于进光量等问题,这类相机一般只有140度左右的成像视野。
一般的畸变模型的设计以针孔相机模型为基础,通过参数模型修正真实的成像与针孔成像的差异,因为在很多的应用中我们希望能够通过“去畸变”的方式,将图片变成“直线还是直线(Straight lines are straight),在KannalaBrandt论文中是这样描述的:
It is impossible to project the hemispherical field of view on a finite image plane by a perspective projection so fish-eye lenses are designed to obey some other projection model.This is the reason why the inherent distortion of a fish-eye lens should not be considered only as a deviation from the pinhole model
于是,就有很多专门针对全景相机(Omidirection Camera/Fisheye Camera/Wide-Angle camera)的建模研究出现。
重新理清一下我们的目的:
-
拥有一种统一的表达方式能够尽量拟合真实的全景相机的成像过程
-
这种表达方式应该简洁有效
-
能够对模型的参数求解,并将图像通过“去畸变”变成像是由针孔相机拍摄出来的横平竖直的图像
OpenCV中针对全景相机的标定和去畸变给出了两种实现
-
KannalaBrandt模型.对应实现OpenCV::Fisheye
-
CMei模型. 对应实现OpenCV::Omnidir
下面简单介绍这两种模型
KannalaBrandt模型
第一步还是先将点投影到单位球模型,这样我们就得出了两个角度,后续的畸变模型就是关于这两个角度的函数
这里这里摘录OpenCV的描述方式OpenCV_Fisheye,相比于论文,在模型参数上简化了很多
KannalaBrandt模型使用一个多项式描述径向畸变(畸变的对称部分):
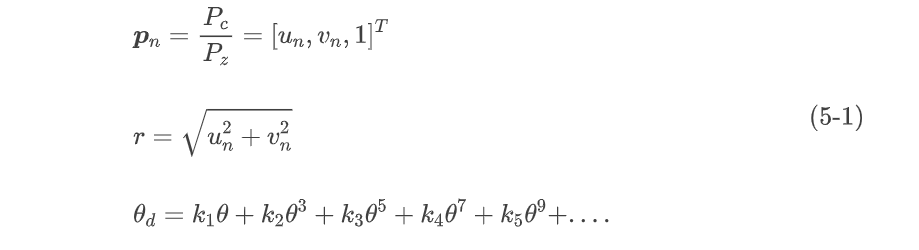
径向畸变后坐标变为:
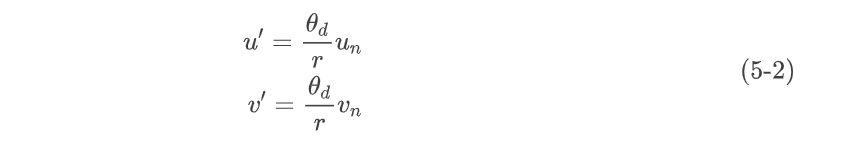
最后再进行非对称畸变:

最后再经过公式(3-5)变换到图像坐标系。
CMei模型
CMei模型相比于其他模型有一个较大不同之处在于在从单位球投影到归一化平面时将相机光心往后移动了距离,总体的投影过程如下图:
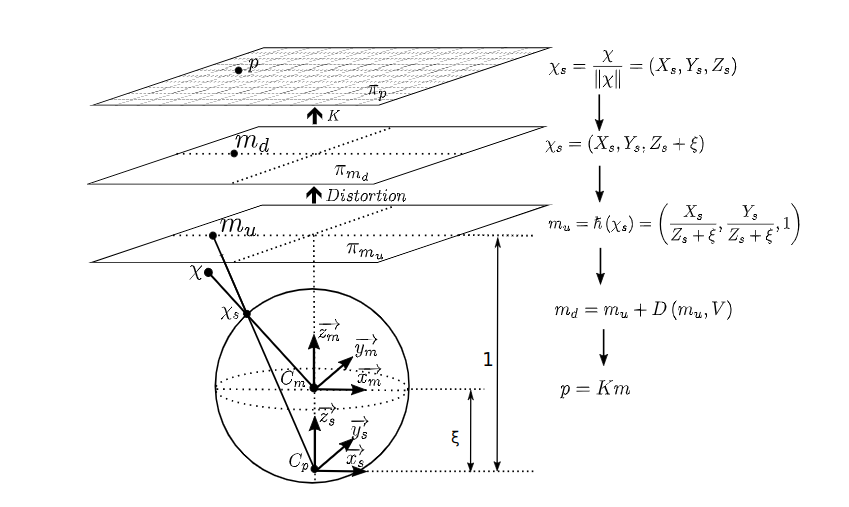
上图出自引用CMei的一篇论文:Design and Calibration of an Omni-RGB+D Camera。
6. 代码实例
实例一:针孔投影模型去畸变
# undistort image
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(K, distortions, (w,h), alpha, (w,h))
undistorted_img = cv2.undistort(img, K, distortions, None, newcameramtx)
x, y, w, h = roi
undistorted_img = undistorted_img[y:y+h, x:x+w]# undistort image points
if points2d.ndim == 2:points2d = points2d[:, None, :]
undistorted_points = cv2.undistortPoints(points2d, K, distortions, P=K)
undistorted_points = undistorted_points.reshape(-1, 2)
实例二:CMei模型去畸变
# undistort image
if newK:K_new = np.zeros((3,3), np.float64)h,w = img.shape[:2]K_new[0, 0] = w/4K_new[0, 2] = w/2K_new[1, 1] = h/4K_new[1, 2] = h/2K_new[2, 2] = 1.0
else:K_new = None
undistorted_img = cv2.omnidir.undistortImage(
img, K, distortions, Xi, cv2.omnidir.RECTIFY_PERSPECTIVE, Knew=K_new)# undistort image points
if points2d.ndim == 2:points2d = points2d[:, None, :]
undistorted_points = cv2.omnidir.undistortPoints(points2d, K, distortions, Xi, None)
undistorted_points = undistorted_points.squeeze()f0 = K_new[0,0]
f1 = K_new[1,1]
c0 = K_new[0,2]
c1 = K_new[1,2]undistorted_points[:, 0] = f0* undistorted_points[:, 0] + c0
undistorted_points[:, 1] = f1 * undistorted_points[:, 1] + c1
PS:cv2::omnidir::undisortPoints的旧版本有bug,参考这个issue。omnidir空间目前还没有成为opencv的正式稳定接口,因此维护在opencv-contrib-python包中,最新的包(4.6.x)已经修复了bug。一定要检查一下是不是有那个bug!!!!
实例三:KannalaBrandt模型去畸变
# You should replace these 3 lines with the output in calibration step
DIM=XXX
K=np.array(YYY)
D=np.array(ZZZ)
def undistort(img_path):img = cv2.imread(img_path)h,w = img.shape[:2]map1, map2 = cv2.fisheye.initUndistortRectifyMap(K, D, np.eye(3), K, DIM, cv2.CV_16SC2)undistorted_img = cv2.remap(img, map1, map2, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT)cv2.imshow("undistorted", undistorted_img)cv2.waitKey(0)cv2.destroyAllWindows()
if __name__ == '__main__':for p in sys.argv[1:]:undistort(p)
7. 相机标定方法
最经典的是使用张正友标定法,可参考另外一篇。
8. 参考资料
-
OpenCV:Camera Calibration
-
OpenCV2.4:Camera Calibration
-
Models for the various classical lens projections
-
Wiki:Distortion
-
KannalaBrandt:A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses
-
CMei: Single View Point Omnidirectional Camera Calibration from Planar Grids
-
OpenCV::Fisheye
-
OpenCV::Omnidir
相关文章:

相机与相机模型(针孔/鱼眼/全景相机)
0. 摘要 本文旨在较为直观地介绍相机成像背后的数学模型,主要的章节组织如下: 第1章用最简单的针孔投影模型为例讲解一个三维点是如何映射到图像中的一个像素 第2章介绍除了针孔投影模型外其他一些经典投影模型,旨在让读者建立不同投影模型…...

ARM32day4
1.思维导图 2.实现三个LED灯亮灭 .text .global _start _start: 使能GPIO外设时钟 LDR R0,0x50000A28 LDR R1,[R0]使能GPIOE ORR R1,R1,#(0X1<<4)使能GPIOF ORR R1,R1,#(0X1<<5) STR R1,[R0]设置引脚状态 LDR R0,0X50006000 LDR R1,[R0] 设置PE10为输出 BIC…...

从零开始写 Docker(六)---实现 mydocker run -v 支持数据卷挂载
本文为从零开始写 Docker 系列第六篇,实现类似 docker -v 的功能,通过挂载数据卷将容器中部分数据持久化到宿主机。 完整代码见:https://github.com/lixd/mydocker 欢迎 Star 推荐阅读以下文章对 docker 基本实现有一个大致认识: …...
网站引用图片但它域名被墙了或者它有防盗链,我们想引用但又不能显示,本文附详细的解决方案非常简单!
最好的办法就是直接读取图片文件,用到php中一个常用的函数file_get_contents(图片地址),意思是读取远程的一张图片,在输出就完事。非常简单~话不多说,直接上代码 <?php header("Content-type: image/jpeg&quo…...

Java八股文(RabbitMQ)
Java八股文のRabbitMQ RabbitMQ RabbitMQ RabbitMQ 是什么?它解决了哪些问题? RabbitMQ 是一个开源的消息代理中间件,用于在应用程序之间进行可靠的异步消息传递。 它解决了应用程序间解耦、消息传递、负载均衡、故障恢复等问题。 RabbitMQ …...
)
科研学习|论文解读——一种用于短文本消息中的释义检测的深度网络模型(IPM, 2018)
论文原标题 A deep network model for paraphrase detection in short text messages 摘要 本文研究释义检测,即识别语义相同的句子。检测用自然语言编写的相似句子的能力对一些应用程序至关重要,如文本挖掘、文本摘要、剽窃检测、作者身份认证和问题回答。认识到这一…...

鸿蒙Harmony应用开发—ArkTS声明式开发(基础手势:Web)下篇
onRequestSelected onRequestSelected(callback: () > void) 当Web组件获得焦点时触发该回调。 示例: // xxx.ets import web_webview from ohos.web.webviewEntry Component struct WebComponent {controller: web_webview.WebviewController new web_webv…...
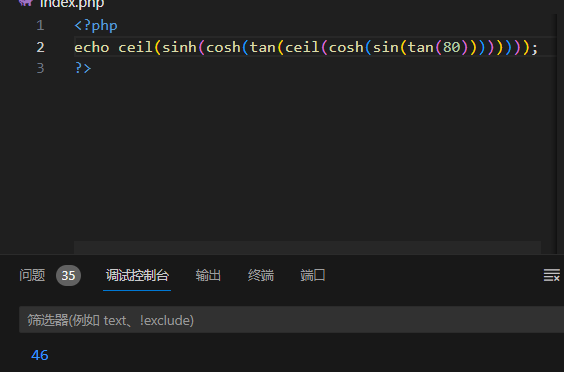
3月19日做题
[NPUCTF2020]验证🐎 if (first && second && first.length second.length && first!second && md5(firstkeys[0]) md5(secondkeys[0]))用数组绕过first1&second[1] 这里正则规律过滤位(Math.) (?:Math(?:\.\w)?) : 匹配 …...
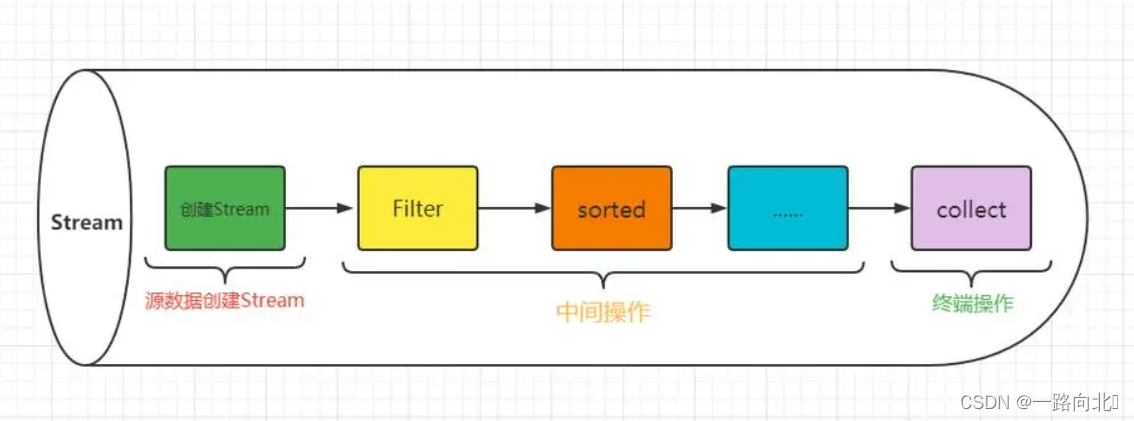
Java8中Stream流API最佳实践Lambda表达式使用示例
文章目录 一、创建流二、中间操作和收集操作筛选 filter去重distinct截取跳过映射合并多个流是否匹配任一元素:anyMatch是否匹配所有元素:allMatch是否未匹配所有元素:noneMatch获取任一元素findAny获取第一个元素findFirst归约数值流的使用中…...

构建Helm chart和chart使用管道与函数简介
目录 一.创建helm chart(以nginx为例) 1.通过create去创建模板 2.查看模板下的文件 3.用chart模版安装nginx 二.版本更新和回滚问题 1.使用upgrade -f values.yaml或者命令行--set来设置 2.查看历史版本并回滚 三.helm模板内管道和函数 1.defau…...

深入理解OnCalculate函数的运行机制
文章目录 一、学习 OnCalculate 函数的运行原理的意义二、OnCalculate 函数原型三、OnCalculate 函数在MT4与MT5区别四、OnCalculate 函数的运行原理 一、学习 OnCalculate 函数的运行原理的意义 OnCalculate函数是MQL语言中的一个重要函数,它用于计算技术指标的值。…...

快速从0-1完成聊天室开发——环信ChatroomUIKit功能详解
聊天室是当下泛娱乐社交应用中最经典的玩法,通过调用环信的 IM SDK 接口,可以快速创建聊天室。如果想根据自己业务需求对聊天室应用的 UI界面、弹幕消息、礼物打赏系统等进行自定义设计,最高效的方式则是使用环信的 ChatroomUIKit 。 文档地址…...

nginx实现多个域名和集群
要通过Nginx实现多个域名和集群,你需要配置Nginx作为反向代理服务器,将来自不同域名的请求转发到集群中的相应后端服务器。下面是一个基本的配置示例,你可以根据自己的需求进行修改和扩展。 首先,确保你已经安装了Nginxÿ…...

C. Left and Right Houses
Problem - C - Codeforces 题目分析 <1>0:想被分割至左边; 1:想被分割至右边 <2>使得左右两侧均有一半及其以上的人满意(我*******) <3>答案若有多个,取最接近中间位置的答案 <4…...

缓存与内存:加速你的Python应用
在现代计算中,缓存和内存是提高程序性能的关键组件。在这篇文章中,我们将深入探讨这两个概念,了解它们是如何工作的,以及如何在Python中有效地使用它们来优化你的程序。 缓存与内存:加速你的Python应用 缓存和内存&…...

Go语言之函数、方法、接口
一、函数 函数的基本语法: func 函数名(形参列表)(返回值列表) {执行语句...return 返回值列表 } 1.形参列表:表示函数的输入 2.函数中的语句:表示为了实现某一功能的代码块 3.函数可以有返回…...
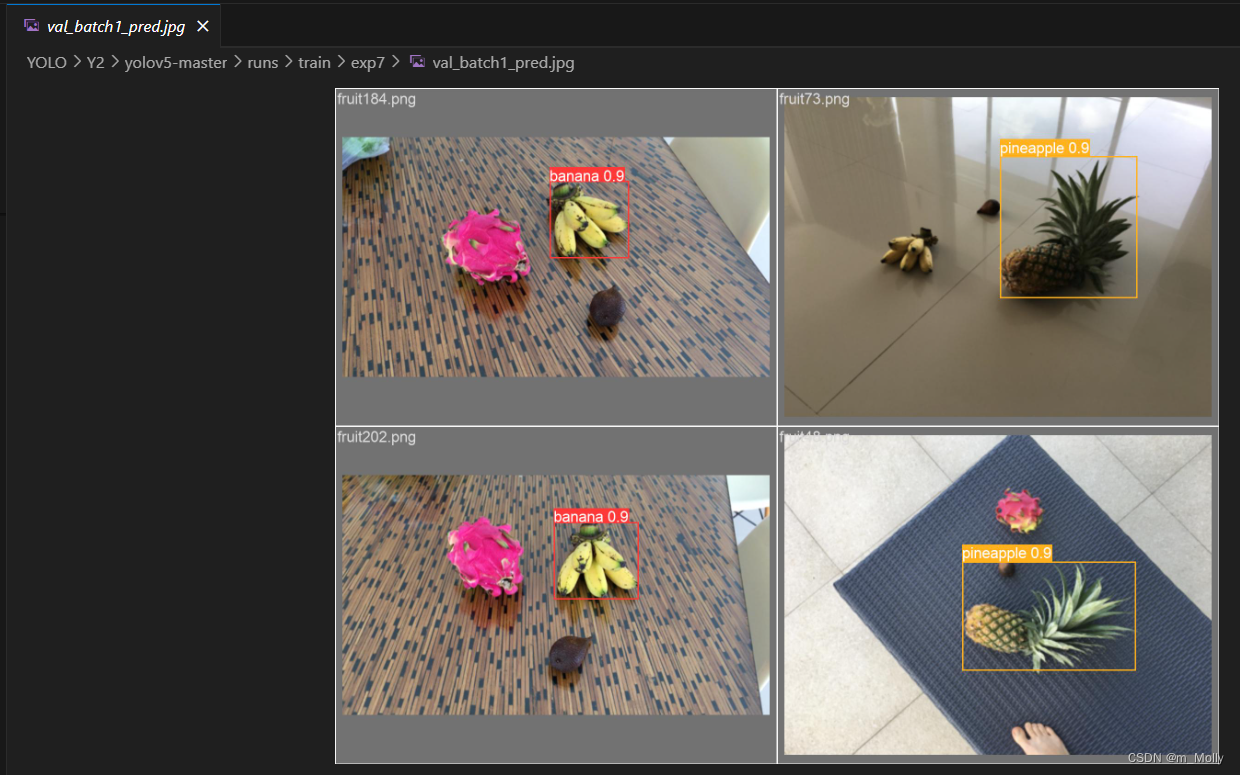
【Week Y2】使用自己的数据集训练YOLO-v5s
Y2-使用自己的数据集训练YOLO-v5s 零、遇到的问题汇总(1)遇到git的import error(2)Error:Dataset not found(3)Error:删除中文后,训练图片路径不存在 一、.xml文件里保存…...

蓝桥杯--基础(哈夫曼)
import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.Scanner;public class BASIC28 {//哈夫曼书public static void main(String[] args) {Scanner Scannernew Scanner(System.in);int nScanner.nextInt();List<Integer&…...

【Redis内存数据库】NoSQL的特点和应用场景
前言 Redis作为当今最流行的内存数据库,已经成为服务端加速的必备工具之一。 NoSQL数据库采用了非关系型的数据存储模型,能够更好地处理海量数据和高并发访问。 内存数据库具有更快的读写速度和响应时间,因为内存访问速度比磁盘访问速度快…...

JavaScript基础知识2
求数组的最大值案例 let arr[2,6,1,7,400,55,88,100]let maxarr[0]let minarr[0]for(let i1;i<arr.length;i){max<arr[i]?maxarr[i]:maxmin>arr[i]?minarr[i]:min}console.log(最大值是:${max})console.log(最小值是:${min}) 操作数组 修改…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
