周赛335(模拟、质因子分解、分组背包)
题解:0x3f
https://leetcode.cn/problems/number-of-ways-to-earn-points/solution/fen-zu-bei-bao-pythonjavacgo-by-endlessc-ludl/
文章目录
- 周赛335
- [6307. 递枕头](https://leetcode.cn/problems/pass-the-pillow/)
- 模拟
- [6308. 二叉树中的第 K 大层和](https://leetcode.cn/problems/kth-largest-sum-in-a-binary-tree/)
- [2584. 分割数组使乘积互质](https://leetcode.cn/problems/split-the-array-to-make-coprime-products/)
- 质因子分解+区间合并
- [2585. 获得分数的方法数](https://leetcode.cn/problems/number-of-ways-to-earn-points/)
- 分组背包
周赛335
6307. 递枕头
难度简单4
n 个人站成一排,按从 1 到 n 编号。
最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾,传递方向就会改变,队伍会继续沿相反方向传递枕头。
- 例如,当枕头到达第
n个人时,TA 会将枕头传递给第n - 1个人,然后传递给第n - 2个人,依此类推。
给你两个正整数 n 和 time ,返回 time 秒后拿着枕头的人的编号。
示例 1:
输入:n = 4, time = 5
输出:2
解释:队伍中枕头的传递情况为:1 -> 2 -> 3 -> 4 -> 3 -> 2 。
5 秒后,枕头传递到第 2 个人手中。
示例 2:
输入:n = 3, time = 2
输出:3
解释:队伍中枕头的传递情况为:1 -> 2 -> 3 。
2 秒后,枕头传递到第 3 个人手中。
提示:
2 <= n <= 10001 <= time <= 1000
模拟
class Solution {public int passThePillow(int n, int time) {n = n-1;boolean rev = false;while(time > n){time -= n;rev = !rev;}return rev ? (n-time+1) : time+1;}
}
6308. 二叉树中的第 K 大层和
难度中等1
给你一棵二叉树的根节点 root 和一个正整数 k 。
树中的 层和 是指 同一层 上节点值的总和。
返回树中第 k 大的层和(不一定不同)。如果树少于 k 层,则返回 -1 。
注意,如果两个节点与根节点的距离相同,则认为它们在同一层。
示例 1:
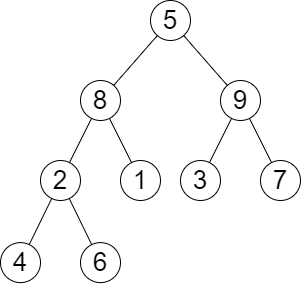
输入:root = [5,8,9,2,1,3,7,4,6], k = 2
输出:13
解释:树中每一层的层和分别是:
- Level 1: 5
- Level 2: 8 + 9 = 17
- Level 3: 2 + 1 + 3 + 7 = 13
- Level 4: 4 + 6 = 10
第 2 大的层和等于 13 。
示例 2:
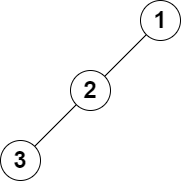
输入:root = [1,2,null,3], k = 1
输出:3
解释:最大的层和是 3 。
提示:
- 树中的节点数为
n 2 <= n <= 1051 <= Node.val <= 1061 <= k <= n
class Solution {public long kthLargestLevelSum(TreeNode root, int k) {PriorityQueue<Long> pq = new PriorityQueue<>();if(root == null) return -1;Deque<TreeNode> dq = new ArrayDeque<>();dq.addLast(root);while(!dq.isEmpty()){int size = dq.size();long sum = 0;while(size-- > 0){TreeNode cur = dq.pollFirst();sum += cur.val;if(cur.left != null) dq.addLast(cur.left);if(cur.right != null) dq.addLast(cur.right);}if(pq.size() < k) pq.add(sum);else{if(pq.peek() < sum){pq.remove();pq.add(sum);}}}return pq.size() < k ? -1 : pq.peek();}
}
2584. 分割数组使乘积互质
难度中等17
给你一个长度为 n 的整数数组 nums ,下标从 0 开始。
如果在下标 i 处 分割 数组,其中 0 <= i <= n - 2 ,使前 i + 1 个元素的乘积和剩余元素的乘积互质,则认为该分割 有效 。
- 例如,如果
nums = [2, 3, 3],那么在下标i = 0处的分割有效,因为2和9互质,而在下标i = 1处的分割无效,因为6和3不互质。在下标i = 2处的分割也无效,因为i == n - 1。
返回可以有效分割数组的最小下标 i ,如果不存在有效分割,则返回 -1 。
当且仅当 gcd(val1, val2) == 1 成立时,val1 和 val2 这两个值才是互质的,其中 gcd(val1, val2) 表示 val1 和 val2 的最大公约数。
示例 1:

输入:nums = [4,7,8,15,3,5]
输出:2
解释:上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
唯一一个有效分割位于下标 2 。
示例 2:

输入:nums = [4,7,15,8,3,5]
输出:-1
解释:上表展示了每个下标 i 处的前 i + 1 个元素的乘积、剩余元素的乘积和它们的最大公约数的值。
不存在有效分割。
提示:
n == nums.length1 <= n <= 1041 <= nums[i] <= 106
质因子分解+区间合并
class Solution {// 互质:左半部分和右半部分没有公共的质因子// 逆向思维:哪些地方不能分割 ==> 区间合并问题 // 如何分解质因子?public int findValidSplit(int[] nums) {int n = nums.length;Map<Integer, Integer> left = new HashMap<Integer, Integer>(); // left[p] 表示质数 p 首次出现的下标int[] right = new int[n]; // right[i] 表示左端点为 i 的区间的右端点的最大值for (int i = 0; i < n; i++) {int x = nums[i];for (int d = 2; d * d <= x; ++d) // 分解质因数if (x % d == 0) {if (left.containsKey(d))right[left.get(d)] = i; // 记录左端点对应的右端点的最大值elseleft.put(d, i); // 第一次遇到质数 dfor (x /= d; x % d == 0; x /= d) ;}if (x > 1) // 找到了一个质因子 xif (left.containsKey(x))right[left.get(x)] = i;elseleft.put(x, i);}for(int l = 0, maxR = 0; l < n; l++){if(l > maxR){// 最远可以遇到 maxRreturn maxR;}maxR = Math.max(maxR, right[l]);}return -1;}
}
2585. 获得分数的方法数
难度困难11
考试中有 n 种类型的题目。给你一个整数 target 和一个下标从 0 开始的二维整数数组 types ,其中 types[i] = [counti, marksi] 表示第 i 种类型的题目有 counti 道,每道题目对应 marksi 分。
返回你在考试中恰好得到 target 分的方法数。由于答案可能很大,结果需要对 109 +7 取余。
注意,同类型题目无法区分。
- 比如说,如果有
3道同类型题目,那么解答第1和第2道题目与解答第1和第3道题目或者第2和第3道题目是相同的。
示例 1:
输入:target = 6, types = [[6,1],[3,2],[2,3]]
输出:7
解释:要获得 6 分,你可以选择以下七种方法之一:
- 解决 6 道第 0 种类型的题目:1 + 1 + 1 + 1 + 1 + 1 = 6
- 解决 4 道第 0 种类型的题目和 1 道第 1 种类型的题目:1 + 1 + 1 + 1 + 2 = 6
- 解决 2 道第 0 种类型的题目和 2 道第 1 种类型的题目:1 + 1 + 2 + 2 = 6
- 解决 3 道第 0 种类型的题目和 1 道第 2 种类型的题目:1 + 1 + 1 + 3 = 6
- 解决 1 道第 0 种类型的题目、1 道第 1 种类型的题目和 1 道第 2 种类型的题目:1 + 2 + 3 = 6
- 解决 3 道第 1 种类型的题目:2 + 2 + 2 = 6
- 解决 2 道第 2 种类型的题目:3 + 3 = 6
示例 2:
输入:target = 5, types = [[50,1],[50,2],[50,5]]
输出:4
解释:要获得 5 分,你可以选择以下四种方法之一:
- 解决 5 道第 0 种类型的题目:1 + 1 + 1 + 1 + 1 = 5
- 解决 3 道第 0 种类型的题目和 1 道第 1 种类型的题目:1 + 1 + 1 + 2 = 5
- 解决 1 道第 0 种类型的题目和 2 道第 1 种类型的题目:1 + 2 + 2 = 5
- 解决 1 道第 2 种类型的题目:5
示例 3:
输入:target = 18, types = [[6,1],[3,2],[2,3]]
输出:1
解释:只有回答所有题目才能获得 18 分。
提示:
1 <= target <= 1000n == types.length1 <= n <= 50types[i].length == 21 <= counti, marksi <= 50
分组背包
class Solution {private static final int MOD = (int) 1e9 + 7;public int waysToReachTarget(int target, int[][] types) {int[] f = new int[target+1];f[0] = 1;for(int[] p : types){int count = p[0], marks = p[1];for(int j = target; j > 0; j--){for(int k = 1; k <= count && k <= j / marks; k++){f[j] = (f[j] + f[j-k*marks]) % MOD;}}}return f[target];}
}
int count = p[0], marks = p[1];for(int j = target; j > 0; j--){for(int k = 1; k <= count && k <= j / marks; k++){f[j] = (f[j] + f[j-k*marks]) % MOD;}}}return f[target];
}
}
相关文章:

周赛335(模拟、质因子分解、分组背包)
题解:0x3f https://leetcode.cn/problems/number-of-ways-to-earn-points/solution/fen-zu-bei-bao-pythonjavacgo-by-endlessc-ludl/ 文章目录周赛335[6307. 递枕头](https://leetcode.cn/problems/pass-the-pillow/)模拟[6308. 二叉树中的第 K 大层和](https://le…...

【极致简洁】Python tkinter 实现下载工具,你想要的一键获取
嗨害大家好鸭!我是小熊猫~开发环境本次项目案例步骤成品效果【咱追求的就是一个简洁】界面如何开始?1.导入模块2.创建窗口【这步很重要】功能按键1.创建一个下拉列表2.设置下拉列表的值3.设置其在界面中出现的位置 column代表列 row 代表行4.设置下拉列表…...
npm i 安装报错
npm WARN EBADENGINE Unsupported engine { npm WARN… npm WARN deprecated stable0.1.8: Modern JS… 诸如此类的报错。大部分都是因为 node 版本问题!比如node版本无法满足,对应项目里需要的那些模块和依赖所需要的条件。 有些模块对node版本是有要…...
原腾讯QQ空间负责人,T13专家,黄希彤被爆近期被裁员,裁员原因令人唏嘘。。...
点击上方“码农突围”,马上关注这里是码农充电第一站,回复“666”,获取一份专属大礼包真爱,请设置“星标”或点个“在看这是【码农突围】的第 431 篇原创分享作者 l 突围的鱼来源 l 码农突围(ID:smartyuge&…...
【C++】BloomFilter——布隆过滤器
文章目录一、布隆过滤器概念二、布隆过滤器应用三、布隆过滤器实现1.插入2.查找3.删除四、布隆过滤器优缺五、结语一、布隆过滤器概念 布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是…...

【Spring】资源操作管理:Resource、ResourceLoader、ResourceLoaderAware;
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ 资源操作:Spring Resources一、Res…...

【System Verilog基础】automatic自动存储--用堆栈区存储局部变量
文章目录一、C语言的内存分配:BSS、Data、Text、Heap(堆)、Stack(栈)1、1、静态内存分配:BSS、Data1、2、程序执行代码:Text1、3、动态内存分配:Heap(堆)、St…...

看板组件:Bryntum Task Board JS 5.3.0 Crack
一个超级灵活的看板组件,Bryntum Task Board 是一个灵活的看板 Web 组件,可帮助您可视化和管理您的工作。 功能丰富 任务板非常灵活,允许您完全自定义卡片、列和泳道的渲染和样式。借助丰富的 API,您甚至可以在运行时打开或关闭功…...

45 个 Git 经典操作场景,专治不会合代码
git对于大家应该都不太陌生,熟练使用git已经成为程序员的一项基本技能,尽管在工作中有诸如 Sourcetree这样牛X的客户端工具,使得合并代码变的很方便。但找工作面试和一些需彰显个人实力的场景,仍然需要我们掌握足够多的git命令。下…...

MyBatis之动态SQL
目录 一、<if>标签 二、<trim>标签 三、<where>标签 四、<set>标签 五、<foreach>标签 一、<if>标签 当我们在某个平台提交某些信息时,可能都会遇到这样的问题,有些信息是必填信息,有些信息是非必…...
SpringBoot(Tedu)—DAY01——环境搭建
SpringBoot(Tedu)—DAY01——环境搭建 目录SpringBoot(Tedu)—DAY01——环境搭建零、今日目标一、IDEA2021项目环境搭建1.1 通过 ctrl鼠标滚轮 实现字体大小缩放1.2 自动提示设置 去除大小写匹配1.3 设置参数方法自动提示1.4 设定字符集 要求都使用UTF-8编码1.5 设置自动编译二…...
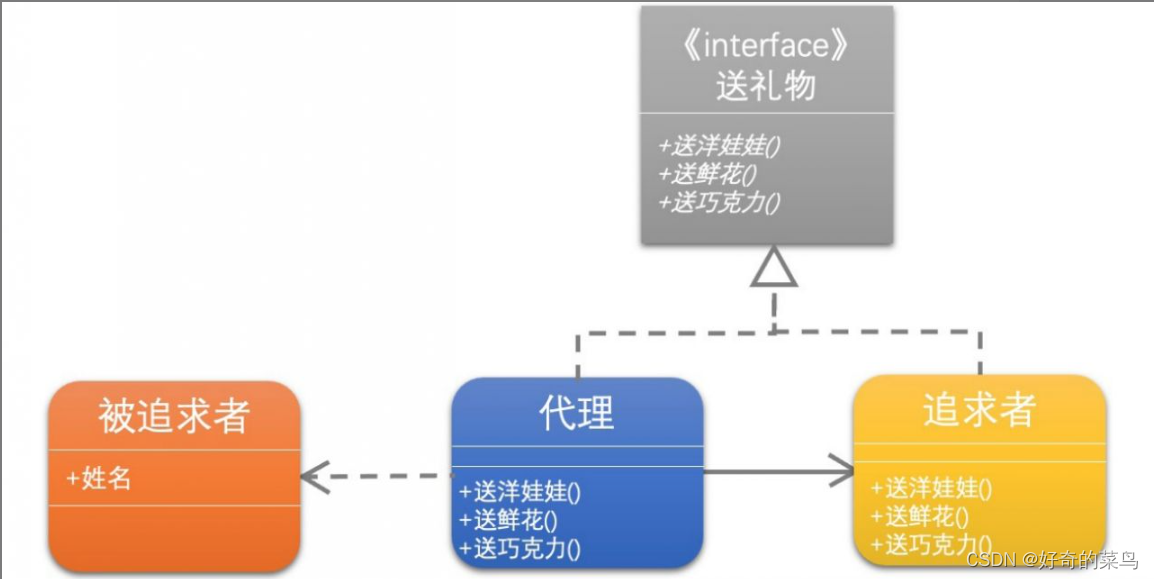
代理模式-大话设计模式
一、定义 代理模式的定义:为其他对象提供一种代理以控制对这个对象的访问。在某些情况下,一个对象不适合或者不能直接引用另一个对象,而代理对象可以在客户端和目标对象之间起到中介的作用。 著名的代理模式例子为引用计数(英语…...

STM32定时器的编码器接口模式
MCU为STM32L431,通用定时器框图: 编码器接口模式一共有三种,通过TIMx_SMCR寄存器的SMS[3:0]位来选择。模式1计数器仅在TI1FP1的边沿根据TI2FP2的电平来判断向上/下计数;模式2计数器仅在TI2FP2的边沿根据TI1FP1的电平来判断向上/下…...
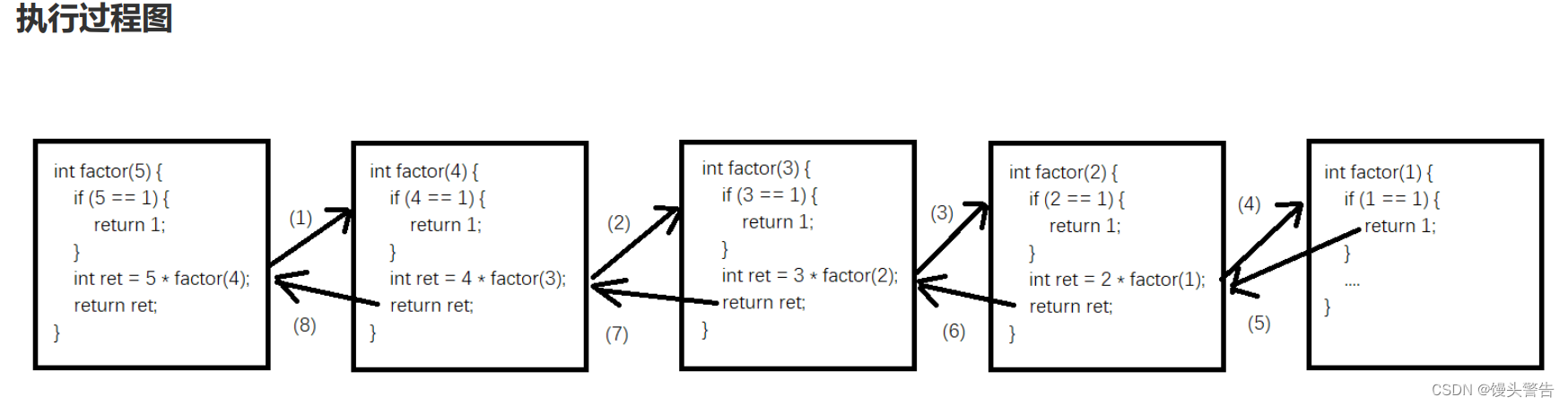
Java方法的使用
目录 一、方法的概念及使用 1、什么是方法(method) 2、方法定义 3、方法调用的执行过程 4、实参和形参的关系 二、方法重载 1、为什么需要方法重载 2、方法重载概念 3、方法签名 三、递归 1、递归的概念 2、递归执行过程分析 一、方法的概念及使用 1、什么是方法(met…...

Linux命令·nl
nl命令在linux系统中用来计算文件中行号。nl 可以将输出的文件内容自动的加上行号!其默认的结果与 cat -n 有点不太一样, nl 可以将行号做比较多的显示设计,包括位数与是否自动补齐 0 等等的功能。 1.命令格式:nl [选项…...
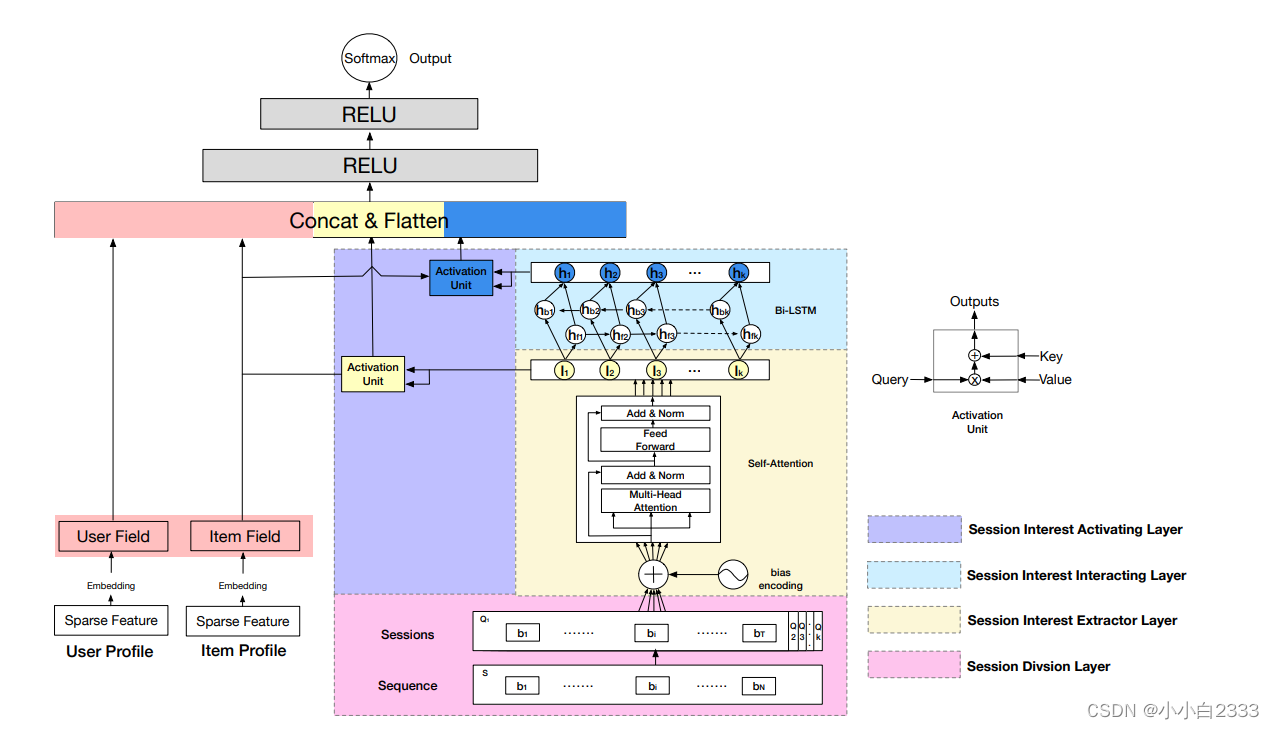
排序模型:DIN、DINE、DSIN
目录 DIN 输入 输出: 与transformer注意力机制的区别与联系: DINE 改善DIN 输入: DSIN 动机: DIN 适用与精排,论文: Deep Interest Network for Click-Through Rate Prediction DIN模型提出的动…...
【C++】Clang-Format:代码自动格式化(看这一篇就够了)
文章目录Clang-format格式化C代码1.引言&安装1.1引言1.2 安装2. 配置字解释2.1 language 编程语言2.2 BaseOnStyle 基础风格2.3 AccessModifierOffset 访问性修饰符偏移2.4 AlignAfterOpenBracket 开括号后的对齐2.5 AlignArrayOfStructures 对齐结构体数组2.6 AlignConsec…...

Linux命令·more
more命令,功能类似 cat ,cat命令是整个文件的内容从上到下显示在屏幕上。 more会以一页一页的显示方便使用者逐页阅读,而最基本的指令就是按空白键(space)就往下一页显示,按 b 键就会往回(back&…...

为什么 SaaS 公司依靠知识库来做对客户服务?
信不信由你,客户服务是您在软件行业赚钱的核心。不仅仅是拥有出色的产品,不仅仅是拥有出色的营销,更重要的是让人们回到您家门口的客户服务。 这是因为从长远来看,留住现有客户比获得新客户更重要,而留住客户时间更长的…...
后端必备之VUE基础【黑马程序员】
黑马程序员4小时入门VUE传送门 1. 简介 Vue是一个操作JavaScript的框架,类似于jQuery,但比jQuery好用,是现在的主流 2. 测试例子 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /&…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
