20240321-2-Adaboost 算法介绍
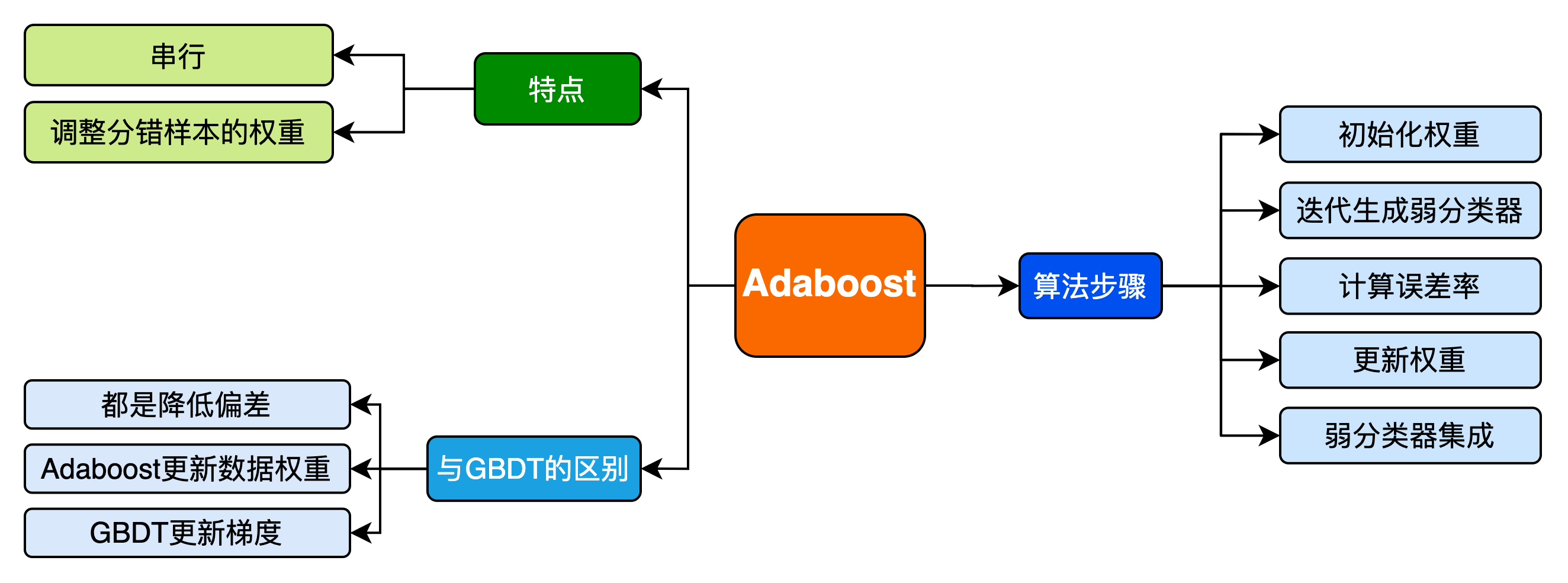
Adaboost 算法介绍
1. 集成学习
集成学习(ensemble learning)通过构建并结合多个学习器(learner)来完成学习任务,通常可获得比单一学习器更良好的泛化性能(特别是在集成弱学习器(weak learner)时)。
目前集成学习主要分为2大类:
一类是以bagging、Random Forest等算法为代表的,各个学习器之间相互独立、可同时生成的并行化方法;
一类是以boosting、Adaboost等算法为代表的,个体学习器是串行序列化生成的、具有依赖关系,它试图不断增强单个学习器的学习能力。
2. Adaboost 算法详解
2.1 Adaboost 步骤概览
-
初始化训练样本的权值分布,每个训练样本的权值应该相等(如果一共有 N N N个样本,则每个样本的权值为 1 N \frac{1}{N} N1)
-
依次构造训练集并训练弱分类器。如果一个样本被准确分类,那么它的权值在下一个训练集中就会降低;相反,如果它被分类错误,那么它在下个训练集中的权值就会提高。权值更新过后的训练集会用于训练下一个分类器。
-
将训练好的弱分类器集成为一个强分类器,误差率小的弱分类器会在最终的强分类器里占据更大的权重,否则较小。
2.2 Adaboost 算法流程
给定一个样本数量为 m m m的数据集
T = { ( x 1 , y 1 ) , … , ( x m , y m ) } T= \left \{\left(x_{1}, y_{1}\right), \ldots,\left(x_{m}, y_{m}\right) \right \} T={(x1,y1),…,(xm,ym)}
y i y_i yi 属于标记集合 { − 1 , + 1 } \{-1,+1\} {−1,+1}。
训练集的在第 k k k个弱学习器的输出权重为
D ( k ) = ( w k 1 , w k 2 , … w k m ) ; w 1 i = 1 m ; i = 1 , 2 … m D(k)=\left(w_{k 1}, w_{k 2}, \ldots w_{k m}\right) ; \quad w_{1 i}=\frac{1}{m} ; i=1,2 \ldots m D(k)=(wk1,wk2,…wkm);w1i=m1;i=1,2…m
- 初始化训练样本的权值分布,每个训练样本的权值相同:
D ( 1 ) = ( w 11 , w 12 , … w 1 m ) ; w 1 i = 1 m ; i = 1 , 2 … m D(1)=\left(w_{1 1}, w_{1 2}, \ldots w_{1 m}\right) ; \quad w_{1 i}=\frac{1}{m} ; i=1,2 \ldots m D(1)=(w11,w12,…w1m);w1i=m1;i=1,2…m
- 进行多轮迭代,产生 T T T个弱分类器。
- 使用权值分布 $D(t) $的训练集进行训练,得到一个弱分类器
G t ( x ) : χ → { − 1 , + 1 } G_{t}(x) : \quad \chi \rightarrow\{-1,+1\} Gt(x):χ→{−1,+1}
- 计算 G t ( x ) G_t(x) Gt(x) 在训练数据集上的分类误差率(其实就是被 $G_t(x) $误分类样本的权值之和):
e t = P ( G t ( x i ) ≠ y i ) = ∑ i = 1 m w t i I ( G t ( x i ) ≠ y i ) e_{t}=P\left(G_{t}\left(x_{i}\right) \neq y_{i}\right)=\sum_{i=1}^{m} w_{t i} I\left(G_{t}\left(x_{i}\right) \neq y_{i}\right) et=P(Gt(xi)=yi)=i=1∑mwtiI(Gt(xi)=yi)
- 计算弱分类器 Gt(x) 在最终分类器中的系数(即所占权重)
α t = 1 2 ln 1 − e t e t \alpha_{t}=\frac{1}{2} \ln \frac{1-e_{t}}{e_{t}} αt=21lnet1−et - 更新训练数据集的权值分布,用于下一轮(t+1)迭代
D ( t + 1 ) = ( w t + 1 , 1 , w t + 1 , 2 , ⋯ w t + 1 , i ⋯ , w t + 1 , m ) D(t+1)=\left(w_{t+1,1} ,w_{t+1,2} ,\cdots w_{t+1, i} \cdots, w_{t+1, m}\right) D(t+1)=(wt+1,1,wt+1,2,⋯wt+1,i⋯,wt+1,m)
w t + 1 , i = w t , i Z t × { e − α t ( i f G t ( x i ) = y i ) e α t ( i f G t ( x i ) ≠ y i ) = w t , i Z t exp ( − α t y i G t ( x i ) ) w_{t+1,i}=\frac{w_{t,i}}{Z_{t}} \times \left\{\begin{array}{ll}{e^{-\alpha_{t}}} & {\text ({ if } G_{t}\left(x_{i}\right)=y_{i}}) \\ {e^{\alpha_{t}}} & {\text ({ if } G_{t}\left(x_{i}\right) \neq y_{i}})\end{array}\right.= \frac{w_{t,i}}{Z_{t}} \exp \left(-\alpha_{t} y_{i} G_{t}\left(x_{i}\right)\right) wt+1,i=Ztwt,i×{e−αteαt(ifGt(xi)=yi)(ifGt(xi)=yi)=Ztwt,iexp(−αtyiGt(xi))
其中 Z t Z_t Zt是规范化因子,使得 D ( t + 1 ) D(t+1) D(t+1)成为一个概率分布(和为1):
Z t = ∑ j = 1 m w t , i exp ( − α t y i G t ( x i ) ) Z_{t}=\sum_{j=1}^{m} w_{t,i} \exp \left(-\alpha_{t} y_{i} G_{t}\left(x_{i}\right)\right) Zt=j=1∑mwt,iexp(−αtyiGt(xi))
- 集成 T T T个弱分类器为1个最终的强分类器:
G ( x ) = sign ( ∑ t = 1 T α t G t ( x ) ) G(x)=\operatorname{sign}\left(\sum_{t=1}^{T} \alpha_{t} G_{t}(x)\right) G(x)=sign(t=1∑TαtGt(x))
3. 算法面试题
3.1 Adaboost分类模型的学习器的权重系数 α \alpha α怎么计算的?
Adaboost是前向分步加法算法的特例,分类问题的时候认为损失函数指数函数。
-
当基函数是分类器时,Adaboost的最终分类器是:
f ( x ) = ∑ m − 1 M α m G m ( x ) = f m − 1 ( x ) + α m G m ( x ) f(x)=\sum_{m-1}^{M}{\alpha_mG_m(x)}=f_{m-1}(x)+{\alpha_mG_m(x)} f(x)=m−1∑MαmGm(x)=fm−1(x)+αmGm(x) -
目标是使前向分步算法得到的 α \alpha α和 G m ( x ) G_m(x) Gm(x)使 f m ( x ) f_m(x) fm(x)在训练数据集T上的指数损失函数最小,即
( α , G m ( x ) ) = a r g m i n α , G ∑ i = 1 N e x p [ − y i ( f m − 1 ( x i ) + α G ( x i ) ) ] (\alpha, G_m(x))=arg min_{\alpha, G}\sum_{i=1}^{N}exp[-y_i(f_{m-1}(x_i)+\alpha G(x_i))] (α,Gm(x))=argminα,Gi=1∑Nexp[−yi(fm−1(xi)+αG(xi))]
其中, w ^ m i = e x p [ − y i f m − 1 ( x i ) ] . \hat{w}_{mi}=exp[-y_i f_{m-1}(x_i)]. w^mi=exp[−yifm−1(xi)].为了求上式的最小化,首先计算 G m ∗ ( x ) G_m^*(x) Gm∗(x),对于任意的 α > 0 \alpha >0 α>0,可以转化为下式:
G m ∗ = a r g m i n G ∑ i = 1 N w ^ m i I ( y i ≠ G ( x i ) ) G_{m}^*=argmin_{G}\sum_{i=1}^{N}\hat{w}_{mi}I(y_i \neq G(x_i)) Gm∗=argminGi=1∑Nw^miI(yi=G(xi))
之后求 α m ∗ \alpha_m^* αm∗,将上述式子化简,得到
∑ i = 1 N w ^ m i e x p [ − y i α G ( x i ) ] = ∑ y i = G m ( x i ) w ^ m i e − α + ∑ y i ≠ G m ( x i ) w ^ m i e α = ( e α − e − α ) ∑ i = 1 N w ^ m i I ( y i ≠ G ( x i ) ) + e − α ∑ i = 1 N w ^ m i \sum_{i=1}^{N}\hat{w}_{mi}exp[-y_i \alpha G(x_i)] = \sum_{y_i =G_m(x_i)}\hat{w}_{mi}e^{-\alpha}+\sum_{y_i \neq G_m(x_i)}{\hat{w}_{mi}e^{\alpha}} = (e^{\alpha} - e^{- \alpha})\sum_{i=1}^{N}\hat{w}_{mi}I(y_i \neq G(x_i)) + e^{- \alpha}\sum_{i=1}^{N}\hat{w}_{mi} i=1∑Nw^miexp[−yiαG(xi)]=yi=Gm(xi)∑w^mie−α+yi=Gm(xi)∑w^mieα=(eα−e−α)i=1∑Nw^miI(yi=G(xi))+e−αi=1∑Nw^mi
将已经求得的 G m ∗ ( x ) G_m^*(x) Gm∗(x)带入上式面,对 α \alpha α求导并等于0,得到最优的 α \alpha α.
a m ∗ = 1 2 l o g 1 − e m e m a_m^*=\frac{1}{2} log{\frac{1-e_m}{e_m}} am∗=21logem1−em
其中 e m e_m em是分类误差率:
e m = ∑ i = 1 N w ^ m i I ( y i ≠ G m ( x i ) ) ∑ i = 1 N w ^ m i = ∑ i = 1 N w ^ m i I ( y i ≠ G m ( x i ) ) e_m=\frac{\sum_{i=1}^{N}\hat{w}_{mi}I(y_i \neq G_m(x_i))}{\sum_{i=1}^{N}\hat{w}_{mi}}=\sum_{i=1}^{N}\hat{w}_{mi}I(y_i \neq G_m(x_i)) em=∑i=1Nw^mi∑i=1Nw^miI(yi=Gm(xi))=i=1∑Nw^miI(yi=Gm(xi))
3.2 Adaboost能否做回归问题?
Adaboost也能够应用到回归问题,相应的算法如下:
输入: T = ( x i , y 1 ) , ( x i , y 1 ) , . . . , ( x N , y N ) T={(x_i, y_1),(x_i, y_1),...,(x_N, y_N)} T=(xi,y1),(xi,y1),...,(xN,yN), 弱学习器迭代次数 M M M。
输出:强分类器 f ( x ) f(x) f(x).
-
初始化权重,
D ( 1 ) = w 11 , w 12 , . . . , w 1 N ; w 1 i = 1 N ; i = 1 , 2 , . . , N D(1)={w_{11},w_{12},...,w_{1N}}; w_{1i}=\frac{1}{N}; i=1,2,..,N D(1)=w11,w12,...,w1N;w1i=N1;i=1,2,..,N -
根据 m = 1 , 2 , . . . , M m=1,2,...,M m=1,2,...,M;
-
学习得到 G m ( x ) G_m(x) Gm(x)
-
计算训练集上最大误差
E m = m a x ∣ y i − G m ( x i ) ∣ , i = 1 , 2 , . . , N E_m=max|y_i-G_m(x_i)|, i=1,2,..,N Em=max∣yi−Gm(xi)∣,i=1,2,..,N -
计算样本的相对平方误差:
e m i = ( y i − G m ( x i ) ) 2 E m 2 e_{mi}=\frac{(y_i-G_m(x_i))^2}{E_m^2} emi=Em2(yi−Gm(xi))2 -
计算回归误差率:
e m = ∑ i = 1 N w m i e m i e_m=\sum_{i=1}^{N}w_{mi}e_{mi} em=i=1∑Nwmiemi -
计算学习器系数:
α m = e m 1 − e m \alpha_m=\frac{e_m}{1-e_m} αm=1−emem -
更新样本权重:
w m + 1 , i = w m i Z m α m 1 − e m , i w_{m+1,i}=\frac{w_{mi}}{Z_m}{\alpha_{m}^{1-e^{m,i}}} wm+1,i=Zmwmiαm1−em,i
其中 Z m Z_m Zm是规范化因子,
Z m = ∑ i = 1 m w m i α m 1 − e m , i Z_m=\sum_{i=1}^{m}w_{mi}{\alpha_{m}^{1-e^{m,i}}} Zm=i=1∑mwmiαm1−em,i
-
-
得到强学习器:
f ( x ) = ∑ m = 1 M G m ∗ ( x ) f(x)=\sum_{m=1}{M}G_{m}^*(x) f(x)=m=1∑MGm∗(x)
注: 不管是分类问题还是回归问题,根据误差改变权重就是Adaboost的本质,可以基于这个构建相应的强学习器。
3.3 boosting和bagging之间的区别,从偏差-方差的角度解释Adaboost?
集成学习提高学习精度,降低模型误差,模型的误差来自于方差和偏差,其中bagging方式是降低模型方差,一般选择多个相差较大的模型进行bagging。boosting是主要是通过降低模型的偏差来降低模型的误差。其中Adaboost每一轮通过误差来改变数据的分布,使偏差减小。
3.4 为什么Adaboost方式能够提高整体模型的学习精度?
根据前向分布加法模型,Adaboost算法每一次都会降低整体的误差,虽然单个模型误差会有波动,但是整体的误差却在降低,整体模型复杂度在提高。
3.5 Adaboost算法如何加入正则项?
f m ( x ) = f m − 1 ( x ) + η α m G m ( x ) f_m(x)=f_{m-1}(x)+\eta \alpha_{m}G_{m}(x) fm(x)=fm−1(x)+ηαmGm(x)
3.6 Adaboost使用m个基学习器和加权平均使用m个学习器之间有什么不同?
Adaboost的m个基学习器是有顺序关系的,第k个基学习器根据前k-1个学习器得到的误差更新数据分布,再进行学习,每一次的数据分布都不同,是使用同一个学习器在不同的数据分布上进行学习。加权平均的m个学习器是可以并行处理的,在同一个数据分布上,学习得到m个不同的学习器进行加权。
3.7 Adaboost和GBDT之间的区别?
相同点:
Adaboost和GBDT都是通过减低偏差提高模型精度,都是前项分布加法模型的一种,
不同点:
Adaboost每一个根据前m-1个模型的误差更新当前数据集的权重,学习第m个学习器;
GBDT是根据前m-1个的学习剩下的label的偏差,修改当前数据的label进行学习第m个学习器,一般使用梯度的负方向替代偏差进行计算。
3.8 Adaboost的迭代次数(基学习器的个数)如何控制?
一般使用earlystopping进行控制迭代次数。
3.9 Adaboost算法中基学习器是否很重要,应该怎么选择基学习器?
sklearn中的adaboost接口给出的是使用决策树作为基分类器,一般认为决策树表现良好,其实可以根据数据的分布选择对应的分类器,比如选择简单的逻辑回归,或者对于回归问题选择线性回归。
3.10 MultiBoosting算法将Adaboost作为Bagging的基学习器,Iterative Bagging将Bagging作为Adaboost的基学习器。比较两者的优缺点?
两个模型都是降低方差和偏差。主要的不同的是顺序不同。MultiBosoting先减低模型的偏差再减低模型的方差,这样的方式
MultiBoosting由于集合了Bagging,Wagging,AdaBoost,可以有效的降低误差和方差,特别是误差。但是训练成本和预测成本都会显著增加。
Iterative Bagging相比Bagging会降低误差,但是方差上升。由于Bagging本身就是一种降低方差的算法,所以Iterative Bagging相当于Bagging与单分类器的折中。
3.11 训练过程中,每轮训练一直存在分类错误的问题,整个Adaboost却能快速收敛,为何?
每轮训练结束后,AdaBoost 会对样本的权重进行调整,调整的结果是越到后面被错误分类的样本权重会越高。而后面的分类器为了达到较低的带权分类误差,会把样本权重高的样本分类正确。这样造成的结果是,虽然每个弱分类器可能都有分错的样本,然而整个 AdaBoost 却能保证对每个样本进行正确分类,从而实现快速收敛。
3.12 Adaboost 的优缺点?
优点:能够基于泛化性能相当弱的的学习器构建出很强的集成,不容易发生过拟合。
缺点:对异常样本比较敏感,异常样本在迭代过程中会获得较高的权值,影响最终学习器的性能表现。
相关文章:

20240321-2-Adaboost 算法介绍
Adaboost 算法介绍 1. 集成学习 集成学习(ensemble learning)通过构建并结合多个学习器(learner)来完成学习任务,通常可获得比单一学习器更良好的泛化性能(特别是在集成弱学习器(weak learner…...
python第三方库的安装,卸载和更新,以及在cmd下pip install安装的包在pycharm不可用问题的解决
目录 第三方库pip安装,卸载更新 1.安装: 2.卸载 3.更新 一、第三方库pip安装,卸载更新 1.安装 pip install 模块名 加镜像下载:pip install -i 镜像网址模块名 常用的是加清华镜像,如 pip install -i https://pyp…...
Python第三次作业
周六 1. 求一个十进制的数值的二进制的0、1的个数 def er(x):a bin(x)b str(a).count("1")c str(a).count("0") - 1print(f"{a},count 1:{b},count 0:{c}")x int(input("enter a number:")) er(x) 2. 实现一个用户管理系统&…...

ai写作软件选哪个?这5款风靡全球的工具不容错过!
从去年到现在,ai 人工智能的发展一直是许多人关注的重点,每隔一段时间新诞生的 ai 工具软件,总会成为人们茶余饭后谈论的焦点。不过在种类繁多的 ai 工具软件中,ai 写作软件是最常被使用的 ai 工具类别,它的使用门槛较…...
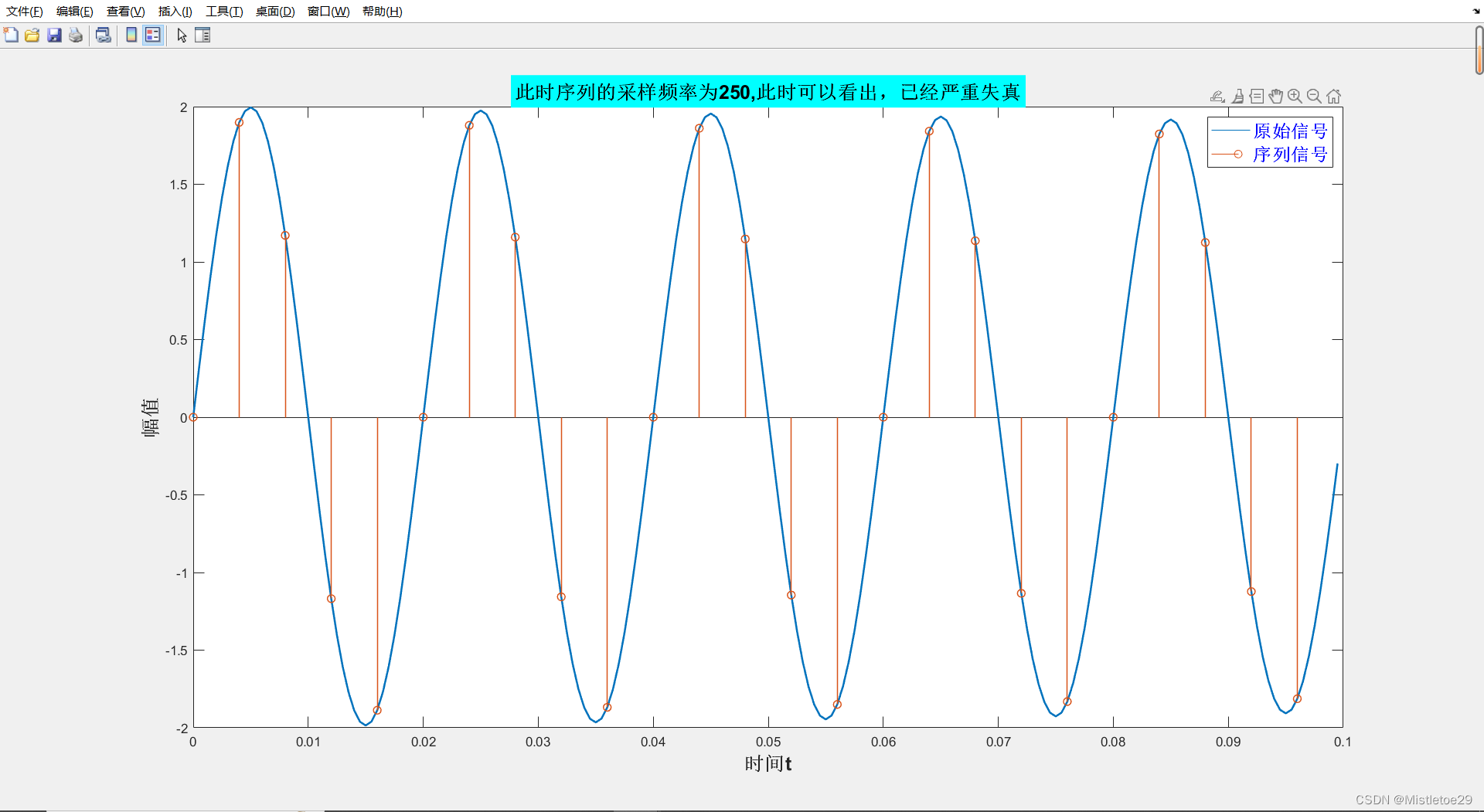
信号处理与分析——matlab记录
一、绘制信号分析频谱 1.代码 % 生成测试信号 Fs 3000; % 采样频率 t 0:1/Fs:1-1/Fs; % 时间向量 x1 1*sin(2*pi*50*t) 1*sin(2*pi*60*t); % 信号1 x2 1*sin(2*pi*150*t)1*sin(2*pi*270*t); % 信号2% 绘制信号图 subplot(2,2,1); plot(t,x1); title(信号x1 1*sin(…...

Android Databinding 使用教程
Android Databinding 使用教程 一、介绍 Android Databinding 是 Android Jetpack 的一部分,它允许你直接在 XML 布局文件中绑定 UI 组件到数据源。通过这种方式,你可以更简洁、更直观地更新 UI,而无需编写大量的 findViewById 和 setText/…...

【每日跟读】常用英语500句(200~300)
【每日跟读】常用英语500句 Home sweet home. 到家了 show it to me. 给我看看 Come on sit. 过来坐 That should do nicely. 这样就很好了 Get dressed now. 现在就穿衣服 If I were you. 我要是你 Close your eyes. 闭上眼睛 I don’t remember. 我忘了 I’m not su…...

【Java开发过程中的流程图】
流程图由一系列的图形符号和箭头组成,每个符号代表一个特定的操作或决策。下面是一些常见的流程图符号及其含义: 开始/结束符号(圆形):表示程序的开始和结束点。 过程/操作符号(矩形)ÿ…...

蓝桥杯刷题-day5-动态规划
文章目录 使用最小花费爬楼梯解码方法 使用最小花费爬楼梯 【题目描述】 给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。 你可以选择从下标为 0 或下标为 1 的台阶…...

新概念英语1:Lesson7内容详解
新概念英语1:Lesson7内容详解 如何询问人的个人信息 本课里有两个关于个人信息的问句,一个是问国籍,一个是问工作,句型如下: what nationality are you?询问国籍 回复一般就是我是哪国人,I’m Chinese…...

FASTAPI系列 14-使用JSONResponse 返回JSON内容
FASTAPI系列 14-使用JSONResponse 返回JSON内容 文章目录 FASTAPI系列 14-使用JSONResponse 返回JSON内容前言一、默认返回的JSON格式二、JSONResponse 自定义返回三、自定义返回 headers 和 media_type总结 前言 当你创建一个 FastAPI 接口时,可以正常返回以下任意…...
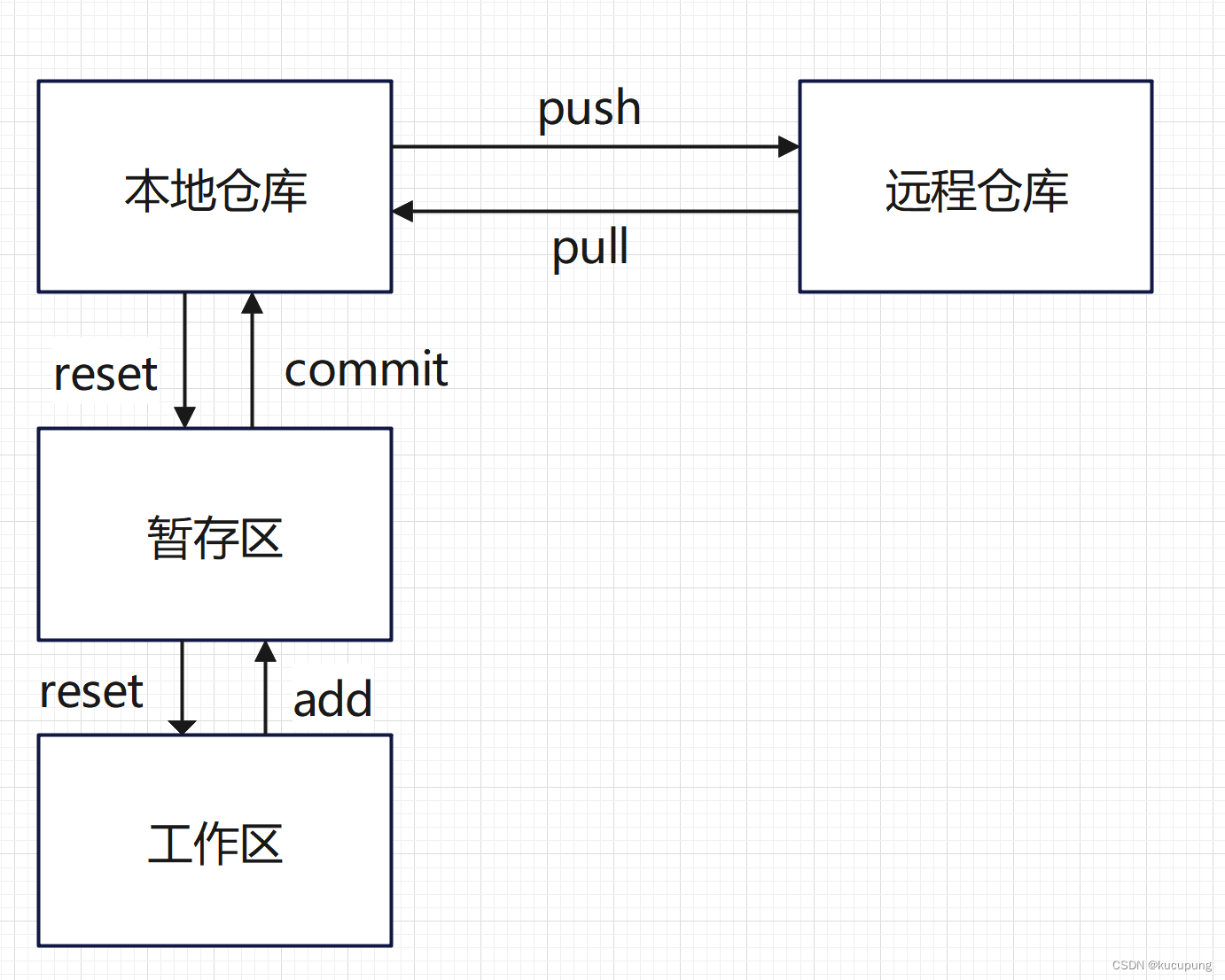
【版本控制】git使用指南
Git 是一个免费、开源的分布式版本控制系统,最初由 Linus Torvalds 于2005年创建。它旨在管理项目的源代码,并提供了跟踪更改、协作开发、版本控制、分支管理等功能。 一、版本控制概念 版本控制系统(Version Control System,VC…...
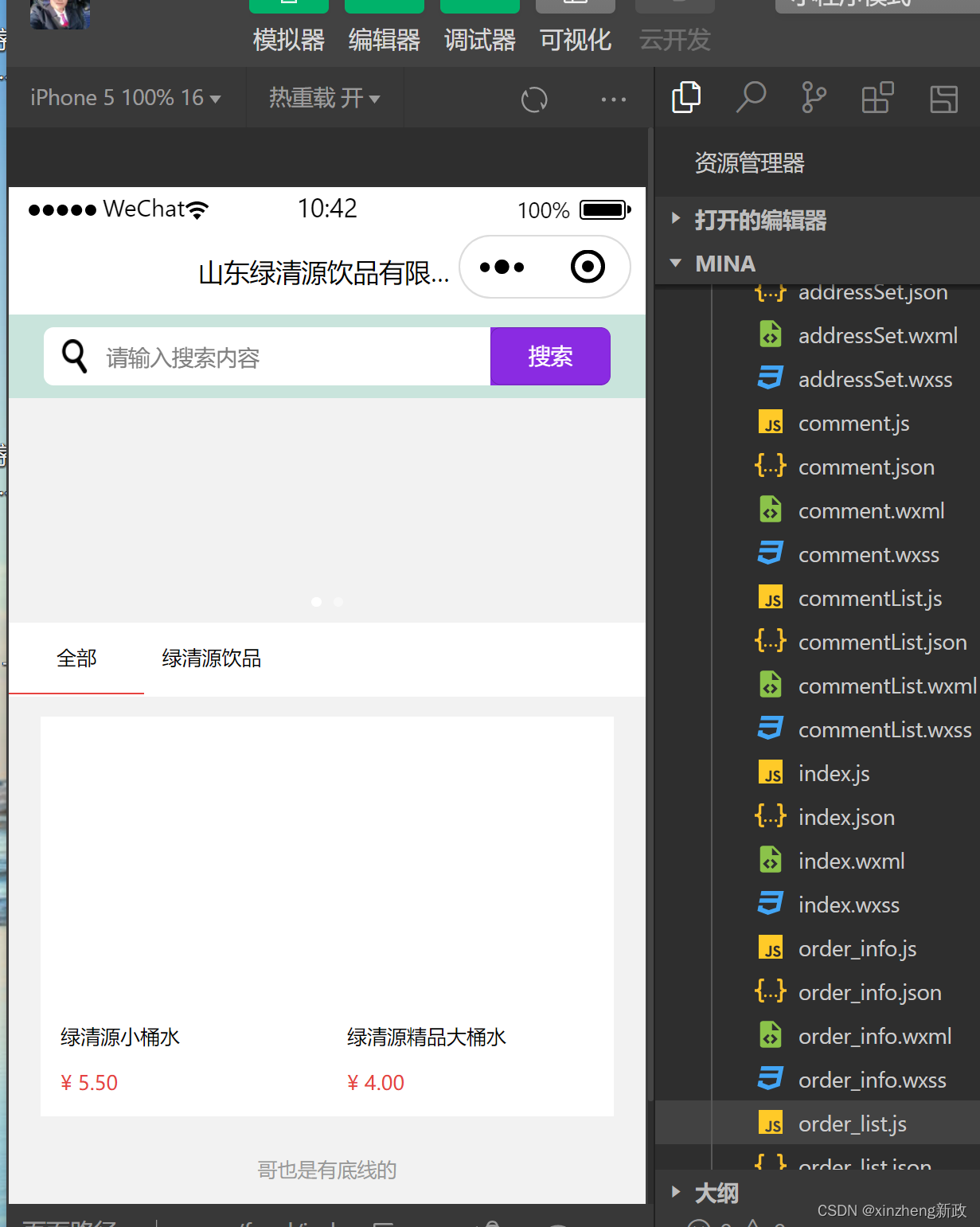
Flask 与小程序 的图片数据交互 过程及探讨研究学习
今天不知道怎么的,之前拿编程浪子地作品抄过来粘上用好好的,昨天开始照片突的就不显示了。 今天不妨再耐味地细细探究一下微信小程序wxml 和flask服务器端是怎么jpg图片数据交互的。 mina/pages/food/index.wxml <!--index.wxml--> <!--1px …...
【JavaEE】初识线程,线程与进程的区别
文章目录 ✍线程是什么?✍线程和进程的区别✍线程的创建1.继承 Thread 类2.实现Runnable接口3.匿名内部类4.匿名内部类创建 Runnable ⼦类对象5.lambda 表达式创建 Runnable ⼦类对象 ✍线程是什么? ⼀个线程就是⼀个 “执行流”. 每个线程之间都可以按…...

Kafka高级面试题-2024
Kafka中的Topic和Partition有什么关系? 在Kafka中,Topic和Partition是两个密切相关的概念。 Topic是Kafka中消息的逻辑分类,可以看作是一个消息的存储类别。它是按照不同的主题对消息进行分类,并且可以用于区分和筛选数据。每个…...
)
Qt——Qt文本读写之QFile与QTextStream的使用总结(打开文本文件,修改内容后保存至该文件中)
【系列专栏】:博主结合工作实践输出的,解决实际问题的专栏,朋友们看过来! 《项目案例分享》 《极客DIY开源分享》 《嵌入式通用开发实战》 《C++语言开发基础总结》 《从0到1学习嵌入式Linux开发》 《QT开发实战》 《Android开发实战》...

掌握Java中的super关键字
super 是 Java 中的一个关键字,它在继承的上下文中特别有用。super 引用了当前对象的直接父类,它可以用来访问父类中的属性、方法和构造函数。以下是 super 的几个主要用途: 1. 调用父类的构造函数 在子类的构造函数中,你可以使…...
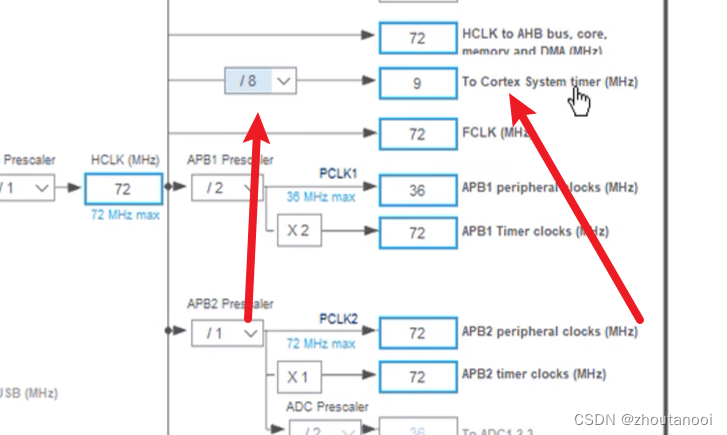
STM32之HAL开发——系统定时器(SysTick)
系统定时器(SysTick)介绍 SysTick—系统定时器是属于 CM3 内核中的一个外设,内嵌在 NVIC 中。系统定时器是一个 24bit的向下递减的计数器,计数器每计数一次的时间为 1/SYSCLK,一般我们设置系统时钟 SYSCLK等于 72M。当…...
Redis 不再“开源”:中国面临的挑战与策略应对
Redis 不再“开源”,使用双许可证 3 月 20 号,Redis 的 CEO Rowan Trollope 在官网上宣布了《Redis 采用双源许可证》的消息。他表示,今后 Redis 的所有新版本都将使用开源代码可用的许可证,不再使用 BSD 协议,而是采用…...
刚刚,百度和苹果宣布联名
百度 Apple 就在刚刚,财联社报道,百度将为苹果今年发布的 iPhone16、Mac 系统和 iOS18 提供 AI 功能。 苹果曾与阿里以及另外一家国产大模型公司进行过洽谈,最后确定由百度提供这项服务,苹果预计采取 API 接口的方式计费。 苹果将…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...

一、ES6-let声明变量【解刨分析最详细】
一、块级作用域 { let Tim"Tim是靓仔!" } console.log("Tim:",Tim) 打印结果:Tim未进行任何定义! 原因:因为Tim定义再块级{}里面,它的声音Tim只服务于该块级里面。而打印结果是再块级外面&#…...

【Mac 从 0 到 1 保姆级配置教程 16】- Docker 快速安装配置、常用命令以及实际项目演示
文章目录 前言1. Docker 是什么?2. 为什么要使用 Docker? 安装 Docker1. 安装 Docker Desktop2. 安装 OrbStack3. Docker Desktop VS OrbStack5. 验证安装 使用 Docker 运行项目1. 克隆项目到本地2. 进入项目目录3. 启动容器: 查看运行效果1. OrbStack 中…...
