蓝桥杯真题Day40 倒计时19天 纯练题!
蓝桥杯第十三届省赛真题-统计子矩阵
题目描述
给定一个 N × M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 × 1,最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式
第一行包含三个整数 N, M 和 K.
之后 N 行每行包含 M 个整数,代表矩阵 A.
输出格式
一个整数代表答案。
样例输入
3 4 10 1 2 3 4 5 6 7 8 9 10 11 12
样例输出
19
提示
满足条件的子矩阵一共有 19,包含:
大小为 1 × 1 的有 10 个。
大小为 1 × 2 的有 3 个。
大小为 1 × 3 的有 2 个。
大小为 1 × 4 的有 1 个。
大小为 2 × 1 的有 3 个。
对于 30% 的数据,N, M ≤ 20. 对于 70% 的数据,N, M ≤ 100.
对于 100% 的数据,1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.
思路提示
1.求每列前缀和(i,j 为上下边界,则可看成用一维解决)。
2.用双指针 l, r 维护左右边界,当 r 边界确定时(找到了 sum > k 的区间),左边界 l 往右移寻找符合条件的区间。

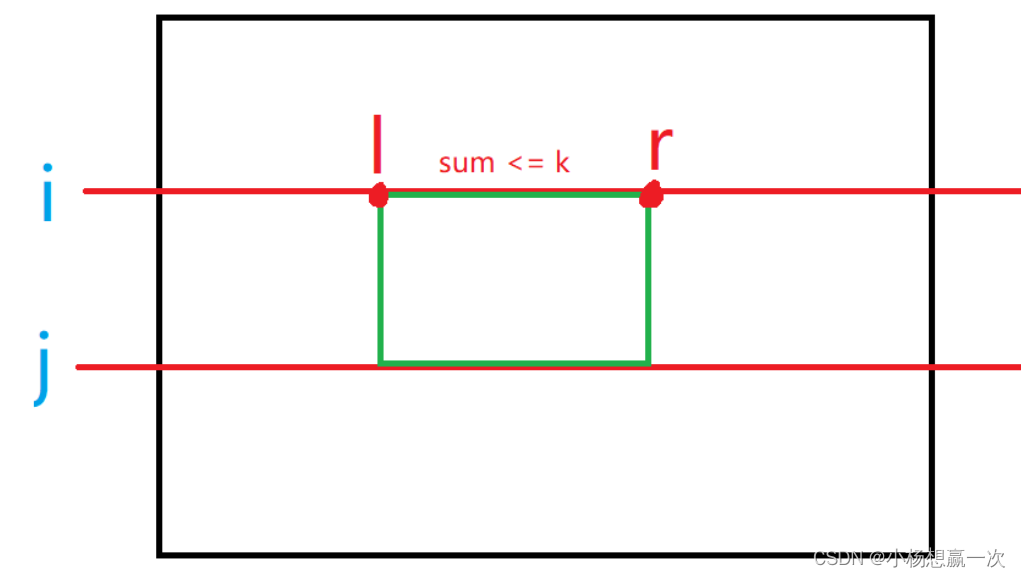
代码表示
#include <bits/stdc++.h>
using namespace std;const int N = 510;
int f[N][N];//二维数组 f可以存储整型数据
int n, m, k;
int main()
{cin >> n >> m >> k;for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )scanf("%d", &f[i][j]),f[i][j] += f[i - 1][j]; // 计算每列前缀和long long res = 0;for (int i = 1; i <= n; i ++ ) // 上边界for (int j = i; j <= n; j ++ ) // 下边界for (int l = 1, r = 1, sum = 0; r <= m; r ++ ){sum += f[j][r] - f[i - 1][r]; // 确定右边界 删去上面的 while (sum > k) // 求符合条件的左边界 l{sum -= f[j][l] - f[i - 1][l];//删除左面的不用的 l ++ ;}res += r - l + 1; }cout << res;return 0;
}心得体会
1、f[i][j] += f[i - 1][j] 时,它的含义是将当前位置 (i, j) 的值加上前一行相同列位置 (i - 1, j) 的值,并将结果保存在当前位置 (i, j)。这是累加前缀和的操作,用于计算子矩阵的和。
2、sum += f[j][r] - f[i - 1][r]; 用于计算当前子矩阵的和。f[j][r] - f[i - 1][r] 表示从上边界 i 到下边界 j、从左边界到右边界 r 的子矩阵的和
3、sum -= f[j][l] - f[i - 1][l]; l ++ ; 通过减去左边界 l 的前缀和,来找到符合条件的左边界。l 逐渐向右移动,直到子矩阵的和不超过 K。
4、res += r - l + 1; 将以当前 (i, j, r) 为边界的子矩阵的个数加到结果变量 res 中。r - l + 1 表示符合条件的子矩阵的列数。
蓝桥杯第十二届省赛真题-砝码称重
题目描述
你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1, W2, · · · , WN。
请你计算一共可以称出多少种不同的重量?
注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 N。
第二行包含 N 个整数:W1, W2, W3, · · · , WN。
输出格式
输出一个整数代表答案。
样例输入
3 1 4 6
样例输出
10
提示
【样例说明】
能称出的 10 种重量是:1、2、3、4、5、6、7、9、10、11。
1 = 1;
2 = 6 4 (天平一边放 6,另一边放 4);
3 = 4 1;
4 = 4;
5 = 6 1;
6 = 6;
7 = 1 + 6;
9 = 4 + 6 1;
10 = 4 + 6;
11 = 1 + 4 + 6。
【评测用例规模与约定】
对于 50% 的评测用例,1 ≤ N ≤ 15。
对于所有评测用例,1 ≤ N ≤ 100,N 个砝码总重不超过 100000。
代码表示
#include <bits/stdc++.h>
using namespace std;
//砝码个数N
const int N = 110, M = 300000;//大一点好
int n,sum,w[N];//总重量 sum
int f[N][M];
int main()
{cin >> n;for (int i = 1;i <= n; i++){//读砝码每一个的重量w[i],累加到总重量 sumcin >> w[i];sum += w[i];}f[0][0]=1; //初始化 for(int i = 1; i <= n; i++){for(int j = 0; j <= sum; j++){//1、f[i-1][j]意味着不选第i个就可以达到重量j//2、f[i-1][j+w[i]]意味着第i个将放在另一边抵消w[i]达到j//3、f[i-1][abs(j-w[i])]意味着用第i个补上w[i]达到jf[i][j] = f[i - 1][j] || f[i - 1][j + w[i]] || f[i - 1][abs(j - w[i])];}}int ans = 0;//从 1 到总重量的所有可能的值 for(int i = 1; i <= sum; i++)//0不可能,故从1开始遍历if(f[n][i]) ans++;cout << ans;return 0;
}心得体会
1、定义一个大小为 N×M 的二维数组 f,其中 f[i][j] 表示在前 i 个砝码中是否可以通过选择一些砝码,使得它们的总重量等于 j。M 的取值为 sum 的两倍,因为最坏情况下,所有砝码都放在一侧,另一侧没有砝码。
2、当我们计算 f[i][j] 时,我们需要考虑前 i 个砝码中是否存在一些砝码的选择,使得它们的总重量等于 j。
- f[i][j] = f[i-1][j+w[i]]:这个转移表示我们选择了第 i 个砝码,并将其放在另一侧以抵消重量 w[i],使得总重量达到 j。因此,我们可以从前 i-1 个砝码中选择一些砝码,使得它们的总重量为 j+w[i]。
- f[i][j] = f[i-1][abs(j-w[i])]:这个转移表示我们选择了第 i 个砝码,并把它加到总重量为 j 的一侧,使得总重量达到 j。因此,我们可以从前 i-1 个砝码中选择一些砝码,使得它们的总重量为 abs(j-w[i])。
这两个转移的含义是根据砝码的放置方式进行考虑的。我们可以选择将第 i 个砝码放在天平的左侧或右侧,或者不选择第 i 个砝码。因此,通过考虑这些不同的放置方式,我们可以计算出 f[i][j] 的值。
3、这个题,一开始拿到就觉得肯定不是简单的正向思维,果然是套者一个东西来做整体遍历的。
蓝桥杯2021年第十二届省赛真题-异或数列
题目描述
Alice 和 Bob 正在玩一个异或数列的游戏。初始时,Alice 和 Bob 分别有一个整数 a 和 b,有一个给定的长度为 n 的公共数列 X1, X2, · · · , Xn。
Alice 和 Bob 轮流操作,Alice 先手,每步可以在以下两种选项中选一种:
选项 1:从数列中选一个 Xi 给 Alice 的数异或上,或者说令 a 变为 a ⊕ Xi。(其中 ⊕ 表示按位异或)
选项 2:从数列中选一个 Xi 给 Bob 的数异或上,或者说令 b 变为 b ⊕ Xi。每个数 Xi 都只能用一次,当所有 Xi 均被使用后(n 轮后)游戏结束。游戏结束时,拥有的数比较大的一方获胜,如果双方数值相同,即为平手。
现在双方都足够聪明,都采用最优策略,请问谁能获胜?
输入格式
每个评测用例包含多组询问。询问之间彼此独立。
输入的第一行包含一个整数 T,表示询问数。
接下来 T 行每行包含一组询问。其中第 i 行的第一个整数 ni 表示数列长度,随后 ni 个整数 X1, X2, · · · , Xni 表示数列中的每个数。
输出格式
输出 T 行,依次对应每组询问的答案。
每行包含一个整数 1、0 或 1 分别表示 Alice 胜、平局或败。
样例输入
4 1 1 1 0 2 2 1 7 992438 1006399 781139 985280 4729 872779 563580
样例输出
1 0 1 1
提示

思路提示
使用res记录所有x的异或结果
1、res==0,平局
2、res!=0,( num数组记录每位的1的个数,从最高位for(i)查看Number[i] )
1)num[i]==1,该位数只要一个1,Alice 先手,胜
2)num[i]是偶数,无影响,不处理
3)num[i]是奇数:① n是偶数,1是奇数,那么0是奇数,只要后手把0先选完,后手就获得最后一个1的支配权,后手胜。②同理可得,n是奇数,0是偶数,先手把0先选完,先手获得最后一个1的支配权,先手胜
3、异或赋值运算符 ^=
4、if(x&1) num[cnt]++;:判断 x 的最低位是否为 1,即 x 的二进制表示的最低位是否为 1。如果是,则将数组 num 中对应位置 cnt 的计数值加 1。
1)x&1 是按位与操作,用来提取 x 的最低位的值。因为 1 的二进制表示为 0001,其他位为 0,所以与 1 进行按位与操作,就可以得到 x 的最低位的值。
2)如果 x 的最低位为 1,说明当前位上有一个 1,所以将数组 num 中对应位 cnt 的计数值加 1。
代码表示
#include <bits/stdc++.h>
using namespace std;int num[22]; //记录每位的1的个数
void pre(int x)//计算一个数的二进制表示中每位上 1 的个数
{int cnt=1;while(x){if(x&1) num[cnt]++;
//将 x 右移一位,即将 x 的二进制表示向右移动一位。x>>=1;cnt++;}
}
int main(){int T; //询问数cin>>T;while(T--){memset(num,0,sizeof(num));int n,res=0; //res存储xi元素异或结果 cin>>n; for(int i=0;i<n;++i){int x;scanf("%d",&x);pre(x);//异或 相同的数异或结果为 0,不同的数异或结果为 1res^=x; }if(res==0){
//平局先手无论怎么选择,后手都可以通过合理的选择使得异或结果保持为 0 printf("0\n"); }else{for(int k=20;k>0;k--){if(num[k]==1){printf("1\n");break;}//1的个数是奇数 if(num[k]%2==1){if(n%2==0){//1是奇数,n是偶数,那么0是奇数,只要后手把0先选完,后手就获得最后一个1的支配权,后手胜 printf("-1\n"); break; }else{
//同理可得,n是奇数,0是偶数,先手把0先选完,先手获得最后一个1的支配权,先手胜利printf("1\n"); break;}}}}}return 0;
}
蓝桥杯第十二届省赛真题-左孩子右兄弟(再看)
题目描述
对于一棵多叉树,我们可以通过 “左孩子右兄弟” 表示法,将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的,那么得到的二叉树可能不唯一。换句话说,每个结点可以选任意子结点作为左孩子,并按任意顺序连接右兄弟。
给定一棵包含 N 个结点的多叉树,结点从 1 至 N 编号,其中 1 号结点是根,每个结点的父结点的编号比自己的编号小。请你计算其通过 “左孩子右兄弟” 表示法转化成的二叉树,高度最高是多少。注:只有根结点这一个结点的树高度为 0 。
例如如下的多叉树:
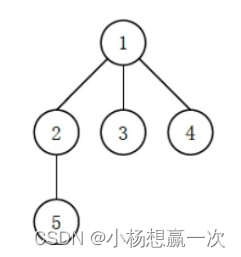
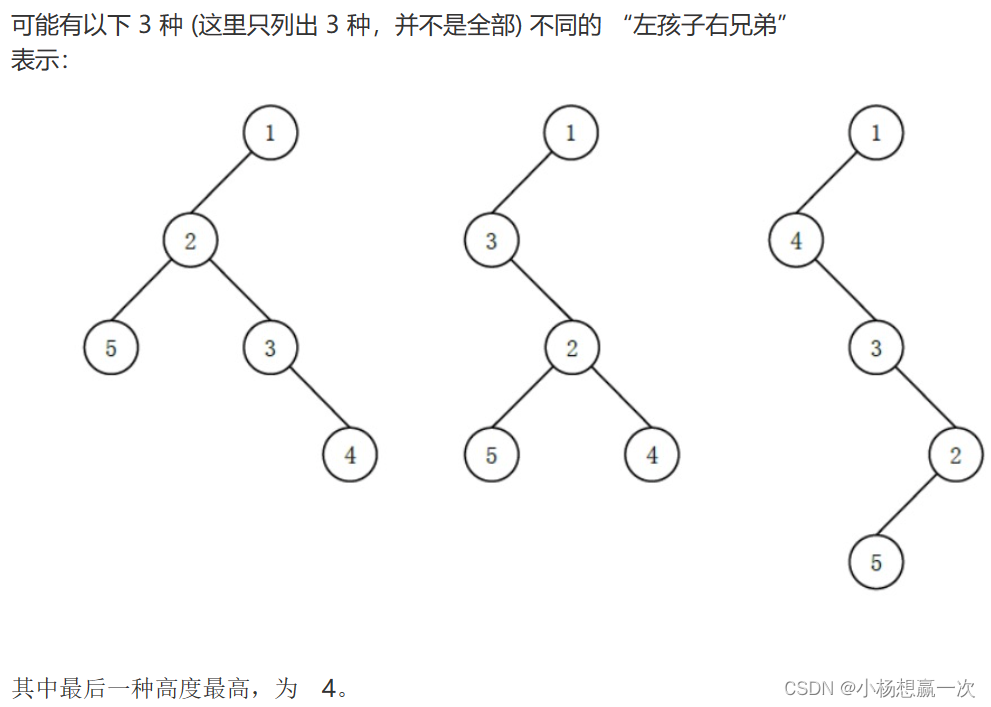
输入格式
输入的第一行包含一个整数 N。
以下 N 1 行,每行包含一个整数,依次表示 2 至 N 号结点的父结点编号。
输出格式
输出一个整数表示答案。
样例输入
5 1 1 1 2
样例输出
4
提示
【评测用例规模与约定】
对于 30% 的评测用例,1 ≤ N ≤ 20;对于所有评测用例,1 ≤ N ≤ 100000。
代码表示
方法一:深搜
对于节点 i,在其子节点中找出:令该节点作为根节点时可以使高度最大的节点 j
令节点 j 作为 i 的子节点中最后一个出现的节点,可使高度达到最大。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;//最大结点数 int n, tmp;
vector<int> mp[MAXN];//存储多叉树的边关系 //递归函数 dfs计算以结点 idx 为根的子树的高度。
int dfs(int idx)
{int sz = mp[idx].size();//获取结点 idx 的子结点的个数int ans = 0;//存储最大高度 for (int i = 0; i < sz; i++) {//更新 ans,取当前子树的高度和已有的最大高度的较大值。 ans = max(ans, dfs(mp[idx][i]));}return ans + sz;//最大子树高度加上当前结点的子结点个数
}int main() {cin >> n;for (int i = 2; i <= n; i++) {cin >> tmp;//读取结点 i 的父结点编号存储到 tmp 中mp[tmp].push_back(i);//将结点 i 添加为结点 tmp 的子结点}cout << dfs(1) << endl;//计算以结点 1 为根的子树的高度return 0;
}方法二:动态规划
用数组 s[i] 表示节点 i 的子节点个数,用数组 f[i] 表示节点 i 的父节点,dp[i] 表示当节点 i 作为根节点时的最大高度,可以推断出如下状态转移方程:dp[ f [ i ] ] = max(dp[ f [ i ] ], s[ f [ i ] ] + dp[ i ]);
由于子节点一定比父节点的编号大,所以对节点编号逆向遍历即可。
1、逆序的循环,从最后一个节点开始,逐步向前遍历每个节点。
在循环中,我们首先通过 int fa = f[i]; 语句获取当前节点 i 的父节点编号,并将其存储在变量 fa 中。然后,我们使用 dp[fa] = max(dp[fa], s[fa] + dp[i]); 更新父节点 fa 的最大高度。这行代码的目的是比较父节点 fa 的当前最大高度 dp[fa] <可能还有其他同级的点>和考虑将当前节点 i 作为子节点时的高度 s[fa] + dp[i],然后取二者中的较大值,并将较大值赋值给 dp[fa],从而更新父节点的最大高度。
这个循环的作用是逐步从叶节点向根节点更新每个节点的最大高度,确保每个节点的最大高度都被正确计算和更新。通过这个过程,我们最终可以得到整棵树的最大高度。
2、dp[fa] 表示节点 fa(父节点)作为根节点时的最大高度。s[fa] 表示节点 fa 的子节点个数。dp[i] 表示节点 i 作为根节点时的最大高度。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100005;//temp:存储读取到的节点 i 的父节点编号
int n, tmp;
//下面分别是子节点个数、父节点和最大高度
int s[MAXN], f[MAXN], dp[MAXN];int main()
{cin >> n;for (int i = 2; i <= n; i++) {cin >> tmp;f[i] = tmp;s[tmp]++;}
//逆向遍历节点编号更新节点 fa 作为根节点时的最大高度for (int i = n; i > 1; i--) {int fa = f[i];//获取结点 i 的父结点编号dp[fa] = max(dp[fa], s[fa] + dp[i]);}cout << dp[1] << endl;return 0;
}
蓝桥杯第十二届省赛真题-括号序列
题目描述
给定一个括号序列,要求尽可能少地添加若干括号使得括号序列变得合法,当添加完成后,会产生不同的添加结果,请问有多少种本质不同的添加结果。两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号。
例如,对于括号序列 (((),只需要添加两个括号就能让其合法,有以下几种不同的添加结果:()()()、()(())、(())()、(()()) 和 ((()))。
输入格式
输入一行包含一个字符串 s,表示给定的括号序列,序列中只有左括号和
右括号。
输出格式
输出一个整数表示答案,答案可能很大,请输出答案除以 1000000007 (即109 + 7) 的余数。
样例输入
((()
样例输出
5
提示
【评测用例规模与约定】
对于 40% 的评测用例,|s| ≤ 200。
对于所有评测用例,1 ≤ |s| ≤ 5000。
代码表示:
#include <bits/stdc++.h>
using namespace std;const int N = 5005;
int f[N][N];
int mod = 1e9 + 7;
string s;
int n;long long get() {memset(f, 0, sizeof f);//memset 将二维数组 f 初始化为全零f[0][0] = 1;for (int i = 1; i <= n; i++) {if (s[i - 1] == '(') {for (int j = 1; j <= n; j++)f[i][j] = f[i - 1][j - 1];//表示在当前位置放置一个左括号} else {
//需要考虑两种情况。
//第一是不将当前位置的括号与之前的任何位置的括号匹配, f[i][0] 的值为 f[i-1][1] + f[i-1][0]。
//第二是将当前位置的括号与之前的某个位置的括号匹配, f[i][j] 的值为 f[i-1][j+1] + f[i][j-1]f[i][0] = (f[i - 1][1] + f[i - 1][0]) % mod;for (int j = 1; j <= n; j++)f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % mod;}}
//我们遍历 f[n] 数组的所有元素,如果某个元素不为零,则返回它作为结果。
//如果所有元素都为零,则返回 -1for (int i = 0; i <= n; i++) {if (f[n][i])return f[n][i];}return -1;
}int main() {cin >> s;n = s.size();long long x = get();reverse(s.begin(), s.end());for (int i = 0; i < n; i++) {if (s[i] == ')')s[i] = '(';elses[i] = ')';}long long y = get();cout << (x * y) % mod;return 0;
}
心得体会:
在赛场上骗分的时候要用所给的示例,确实有一点点的分
相关文章:

蓝桥杯真题Day40 倒计时19天 纯练题!
蓝桥杯第十三届省赛真题-统计子矩阵 题目描述 给定一个 N M 的矩阵 A,请你统计有多少个子矩阵 (最小 1 1,最大 N M) 满足子矩阵中所有数的和不超过给定的整数 K? 输入格式 第一行包含三个整数 N, M 和 K. 之后 N 行每行包含 M 个整数…...

Android 14.0 SystemUI下拉状态栏增加响铃功能
1.概述 在14.0的系统产品rom定制化开发中,在对systemui的状态栏开发中,对SystemUI下拉状态栏的QuickQSPanel区域有快捷功能键开关,对于增加各种响铃快捷也是常用功能, 有需要增加响铃功能开关功能,接下来就来分析SystemUI下拉状态栏QuickQSPanel快捷功能键开关的相关源码…...

docker学习笔记 二-----docker介绍
老套路哈,第一章先科普一下三种常见的云服务类型,第二和第三章节写docker学习笔记。 一 、IAAS、PAAS、SAAS IAAS (Infrastructure as a Service):基础即服务,供应商仅提供给用户最基础设施的服务资源,也就是服务器资…...
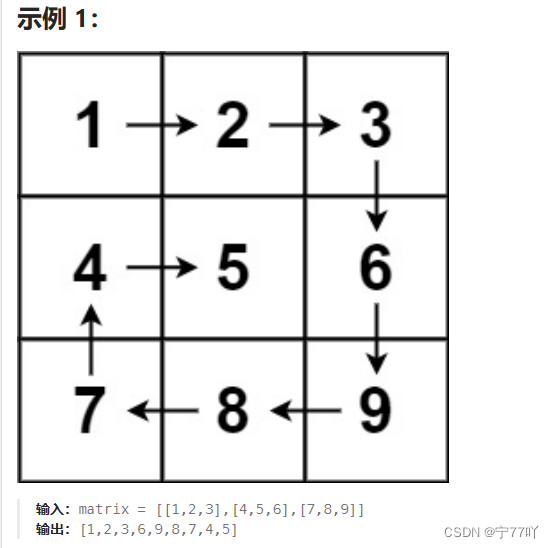
螺旋矩阵的算法刷题
螺旋矩阵的算法刷题 本文主要涉及螺旋矩阵的算法 包括三个题目分别是 59. 螺旋矩阵 II54. 螺旋矩阵 中等LCR 146. 螺旋遍历二维数组 文章目录 螺旋矩阵的算法刷题一 、螺旋矩阵简单1.1 实现一(我认为这个方法更巧妙!!)1.2 实现二&…...
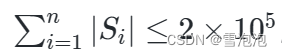
蓝桥杯算法赛(二进制王国)
问题描述 二进制王国是一个非常特殊的国家,因为该国家的居民仅由 0 和 1 组成。 在这个国家中,每个家庭都可以用一个由 0 和 1 组成的字符串 S 来表示,例如 101、 000、 111 等。 现在,国王选了出 N 户家庭参加邻国的庆典…...
7.JDK下载和安装
文章目录 一、下载二、安装三、JDK的安装目录介绍 写JAVA代码不是随随便便能写的,我们得先做一点准备工作。例如,我们平时想要玩一把游戏,就需要先下载、安装才能玩游戏。JAVA也是一样的,也是需要下载并安装相关的软件,…...

Java序列化之Jackson详解
文章目录 1 Jackson1.1 Jackson简介1.2 为什么选择Jackson1.3 Jackson的基本功能1.3.1 将Java对象转换为JSON字符串(序列化)1.3.2 将JSON字符串转换为Java对象(反序列化) 1.4 Jackson库主要方法1.5 使用Jackson基本步骤1.5.1 添加…...

深入Facebook的世界:探索数字化社交的无限可能性
引言 随着数字化时代的到来,社交媒体平台已经成为了人们日常生活中不可或缺的一部分,而其中最为突出的代表之一便是Facebook。作为全球最大的社交媒体平台之一,Facebook不仅仅是一个社交网络,更是一个数字化社交的生态系统&#…...

HTML 怎么解决上下标问题呢?
当我们阅读内容时,经常会遇到特殊格式的文本,如化学式的下标和数学公式的上标,sub 标签和sup 标签就是用来解决这个问题的。 1. 基础语法 什么是 sub 和sup标签 sub 标签用于定义下标文本,而 sup 标签用于定义上标文本。 这些…...

题目 2880: 计算鞍点
题目描述: 给定一个5*5的矩阵,每行只有一个最大值,每列只有一个最小值,寻找这个矩阵的鞍点。 鞍点指的是矩阵中的一个元素,它是所在行的最大值,并且是所在列的最小值。 例如:在下面的例子中(第…...

前端Web移动端学习day05
移动 Web 第五天 响应式布局方案 媒体查询Bootstrap框架 响应式网页指的是一套代码适配多端,一套代码适配各种大小的屏幕。 共有两种方案可以实现响应式网页,一种是媒体查询,另一种是使用bootstrap框架。 01-媒体查询 基本写法 max-wid…...
蚂蚁庄园今日答案
蚂蚁庄园是一款爱心公益游戏,用户可以通过喂养小鸡,产生鸡蛋,并通过捐赠鸡蛋参与公益项目。用户每日完成答题就可以领取鸡饲料,使用鸡饲料喂鸡之后,会可以获得鸡蛋,可以通过鸡蛋来进行爱心捐赠。其中&#…...

深度学习中的随机种子random_seed
在深度学习中,random_seed是一个用于控制随机过程的种子值。这个种子值用于初始化随机数生成器,从而确保在多次实验中,涉及随机性的步骤能够产生一致的结果。这对于实验的可重复性、调试以及结果对比都是至关重要的。 具体来说,深…...

【项目技术介绍篇】若依管理系统功能介绍
作者介绍:本人笔名姑苏老陈,从事JAVA开发工作十多年了,带过大学刚毕业的实习生,也带过技术团队。最近有个朋友的表弟,马上要大学毕业了,想从事JAVA开发工作,但不知道从何处入手。于是࿰…...
)
Maximum Sum(贪心策略,模运算,最大子段和)
文章目录 题目描述输入格式输出格式样例输入1样例输出1样例输入2样例输出2提交链接提示 解析参考代码 题目描述 你有一个由 n n n 个整数组成的数组 a a a 。 你要对它进行 k k k 次操作。其中一个操作是选择数组 a a a 的任意连续子数组(可能为空),并在数组的…...

Gartner 公布 2024 年八大网络安全预测
近日,Gartner 安全与风险管理峰会在悉尼举行,旨在探讨网络安全的发展前景。 本次峰会,Gartner 公布了 2024 年及以后的八大网络安全预测。 Gartner 研究总监 Deepti Gopal 表示,随着 GenAI 的不断发展,一些长期困扰网…...
)
《每天十分钟》-红宝书第4版-对象、类与面向对象编程(六)
盗用构造函数 上节提到原型包含引用值导致的继承问题,为了解决这种问题,一种叫作“盗用构造函数”(constructor stealing)的技术在开发社区流行起来(这种技术有时也称作“对象伪装”或“经典继承”)。基本…...

Ubuntu Desktop Server - user 用户与 root 用户切换
Ubuntu Desktop Server - user 用户与 root 用户切换 1. user 用户与 root 用户切换2. root 用户与 user 用户切换References 1. user 用户与 root 用户切换 strongforeverstrong:~$ strongforeverstrong:~$ sudo su [sudo] password for strong: rootforeverstrong:/home/s…...
SQL Server事务复制操作出现的错误 进程无法在“xxx”上执行sp_replcmds
SQL Server事务复制操作出现的错误 进程无法在“xxx”上执行“sp_replcmds” 无法作为数据库主体执行,因为主体 "dbo" 不存在、无法模拟这种类型的主体,或您没有所需的权限...

学点儿Java_Day12_IO流
1 IO介绍以及分类 IO: Input Output 流是一组有顺序的,有起点和终点的字节集合,是对数据传输的总称或抽象。即数据在两设备间的传输称为流,流的本质是数据传输,根据数据传输特性将流抽象为各种类,方便更直观的进行数据…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...
