美团0316春招笔试题
下面是美团2024-03-16笔试真题,进行了VP,由于未参与评测,故不保证正确性,仅供参考。
第一题 小美点外卖

求和然后减去满减和红包即可。
#include <bits/stdc++.h>
using namespace std;
using LL = long long ;
int n, t, x, y;
LL ans;int main() {scanf("%d", &n);while (n -- ) {scanf("%d", &t);ans += t;}scanf("%d%d", &x, &y);printf("%lld\n", ans - x - y);
}
第二题 小美的合法单词

考虑三种情况分别需要的操作次数,取最小值即可。
先扫描字符串s,并用变量big和small分别统计字符串s中大写字母、小写字母的个数。
然后还要处理第一个字符是大写的情况:
首先初始化变量t=s.size(),当第一个字符是大写字母时,执行t = t - 1 - small。减去1是因为去掉第一个大写字母,然后再减去small,这样得到的就是后面剩余的大写字符个数。
为什么是t-1-small而不是t-1-big呢?举个例子:s=“AaaBbCD”,此时big=4,small=3。
- 若执行t-1-big,则此时t的结果就是2,那么答案为min{big, small, t} = 2,但显然答案应该是3(将后面的B,C,D修改为小写)。
- 若执行t-1-small,则此时t的结果就是3,那么答案为min{big, small, t} = 3,这显然就是正确答案3(将后面的B,C,D修改为小写)。
说白了就是由于题目要求第一个字母大写,后面所有字母都是小写。t-1-small就是将后面统计除了首位这个大写字母外剩余部分的大写字母个数,而我们需要将这些大写字母个数就是我们需要修改为小写字母所需要的操作次数。
#include <bits/stdc++.h>
using namespace std;int main() {string s;cin >> s;int big = 0, small = 0, t = s.size();for (auto& c : s) {if (c >= 'A' && c <= 'Z') ++ big;else if (c >= 'a' && c <= 'z') ++ small;}if (s[0] >= 'A' && s[0] <= 'Z') t = t - 1 - small;printf("%d\n", min({small, big, t}));
}
第三题 翻倍元素

统计每个元素最后翻倍的次数即可。
如下表:
| 数组元素a[] | 翻倍次数times[] | 最终结果 |
|---|---|---|
| a[1]=1 | 1 | 1 × 2 1 1\times 2^1 1×21 |
| a[2]=2 | 1 | 2 × 2 1 2\times 2^1 2×21 |
| a[3]=3 | 2 | 3 × 2 2 3\times 2^2 3×22 |
| a[4]=4 | 2 | 4 × 2 2 4\times 2^2 4×22 |
因此最终结果为2、4、12、16,答案即为2+4+12+16=34。
对于快速求 a b a^b ab显然可以使用快速幂。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, MOD = 1e9 + 7;
int a[N], times[N], n, m;int qmi(int a, int b) {int ans = 1;while (b) {if (b & 1) ans = ans * a % MOD;a = a * a % MOD;b >>= 1;}return ans % MOD;
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; ++ i) {scanf("%d", &a[i]);times[i] = m;}for (int i = 1; i <= m; ++ i) {int x;scanf("%d", &x);-- times[x];}int ans = 0;for (int i = 1; i <= n; ++ i) {ans = (ans + a[i] * qmi(2, times[i]) % MOD) % MOD;}printf("%d\n", ans);
}
第四题 小美的众数

首先需要观察到元素 a i a_i ai只有1和2这两种取值。由于它的数值只有1和2,所以记录一个前缀和。如果说当前值是1就前缀和加1,如果说当前值是2,就前缀和减1。即我们定义数组 s i s_i si表示区间 [ 1 , i ] [1,i] [1,i]中元素1和元素2的被标记为+1和-1之后的前缀和。
对于一个前缀和 s i s_i si来说,它前面有多少个 s j s_j sj的值比 s i s_i si小,就说明,1的个数会大于等于2的个数,那么这些数量的区间,众数必然是元素1。 i i i减去这些区间的数量,也就是剩下的区间数量,众数就是2了。
对于如何求一个前缀和 s i s_i si来说,它前面有多少个 s j s_j sj的值比 s i s_i si小,这可以用树状数组来求解。
为什么要加偏移量OFFSET = n+1呢?
这是因为数组s[]取值有可能是负数(这是由于将元素1和元素2的被标记为+1和-1导致的),最坏情况下s[]取值可能是 − n -n −n。但是我们知道树状数组下标是从1开始的,不能是<1的,故我们加上偏移量n+1,使得保证树状数组的下标是正确从1开始。
如何理解query(s[i] + OFFSET) + (i - query(s[i] + OFFSET)) * 2这个式子呢?
query(s[i] + OFFSET)其实完整写法是query(s[i] + OFFSET) * 1,它求解的是如果当前区间 [ 1 , i ] [1,i] [1,i]中的众数是元素1的话,那么就求这些子区间中众数1的总和。(i - query(s[i] + OFFSET)) * 2,它求解的是如果当前区间 [ 1 , i ] [1,i] [1,i]中的众数是元素1的话,那么就求这些子区间中众数1的总和。当前有 i i i个元素,其中众数是元素1的个数有query(s[i] + OFFSET)个,那么众数是元素2的个数就为(i - query(s[i] + OFFSET))。然后求这些子区间中众数2的总和即可。
#include <bits/stdc++.h>
const int N = 2e5 + 10;
using LL = long long ;
int a[N], s[N], tr[N * 2], n;inline int lowbit(int x) {return x & -x;
}void modify(int x, int k) {for (int i = x; i <= 2 * n + 10; i += lowbit(i)) tr[i] += k;
}LL query(int x) {LL ans = 0;for (int i = x; i; i -= lowbit(i)) ans += tr[i];return ans;
}int main() {scanf("%d", &n);int OFFSET = n + 1; // 偏移量,防止下标是负数,使得下标从1开始for (int i = 1; i <= n; ++ i) scanf("%d", &a[i]);modify(0 + OFFSET, 1); // 边界初始化!!!LL ans = 0;for (int i = 1; i <= n; ++ i) {if (a[i] == 1) s[i] += s[i - 1] + 1;else s[i] += s[i - 1] - 1;// query(s[i] + OFFSET) * 1计算出如果1是众数时的和// (i - query(s[i] + OFFSET)) * 2计算出如果2是众数时的和ans += query(s[i] + OFFSET) + (i - query(s[i] + OFFSET)) * 2;modify(s[i] + OFFSET, 1);}printf("%lld", ans);
}
第五题 小美的逆序对

本题可以考虑使用树状数组来求逆序对。
我们可以先对原数组求一遍逆序对。对于第 i i i个数字,它在变为最小的数字后,在它之前的所有比它小的数字都会和它组成逆序对,在它之后所有比它小的数字会由原本构成逆序对转变成不构成逆序对。设在它左侧比它小的数字的个数为cnt,那么在它右侧比它小的数字的个数就是x - 1 - cnt。因此当元素x取反后,它左侧这cnt个数字就比x大,增加了cnt个逆序对,然后它右侧这x-1-cnt个数字就比x大,减少了x-1-cnt个逆序对。由此逆序对的增量就是x - (x - 1 - cnt)个。考虑原本的逆序对数目s,则第 i i i个数字取反后的逆序对数目为s + x - (x - 1 - cnt)。
#include <bits/stdc++.h>
const int N = 2e5 + 10;
using LL = long long ;
int t[N], tr[N], n;inline int lowbit(int x) {return x & -x;
}void modify(int x, int k) {for (int i = x; i <= n; i += lowbit(i)) tr[i] += k;
}LL query(int x) {LL ans = 0;for (int i = x; i; i -= lowbit(i)) ans += tr[i];return ans;
}int main() {scanf("%d", &n);LL s = 0;for (int i = 1; i <= n; ++ i) {int x;scanf("%d", &x);s += query(n) - query(x);// cnt表示x左侧比x小的元素个数, x - 1 - cnt表示x右侧比x小的元素个数LL cnt = query(x - 1);t[i] = cnt - (x - 1 - cnt);modify(x, 1);}for (int i = 1; i <= n; ++ i) printf("%lld ", s + t[i]);
}
相关文章:

美团0316春招笔试题
下面是美团2024-03-16笔试真题,进行了VP,由于未参与评测,故不保证正确性,仅供参考。 第一题 小美点外卖 求和然后减去满减和红包即可。 #include <bits/stdc.h> using namespace std; using LL long long ; int n, t, x,…...

typescript 实现RabbitMQ死信队列和延迟队列 订单10分钟未付归还库存
Manjaro安装RabbitMQ 安装 sudo pacman -S rabbitmq rabbitmqadmin启动管理模块 sudo rabbitmq-plugins enable rabbitmq_managementsudo rabbitmq-server管理界面 http://127.0.0.1:15672/ 默认用户名和密码都是guest。 要使用 rabbitmqctl 命令添加用户并分配权限…...

怎样才能把重建大师的空三导进去CC?
导出空三文件xml两者都是通用的,cc和photoscan都可以兼容。 重建大师是一款专为超大规模实景三维数据生产而设计的集群并行处理软件,输入倾斜照片,激光点云,POS信息及像控点,输出高精度彩色网格模型,可一键…...
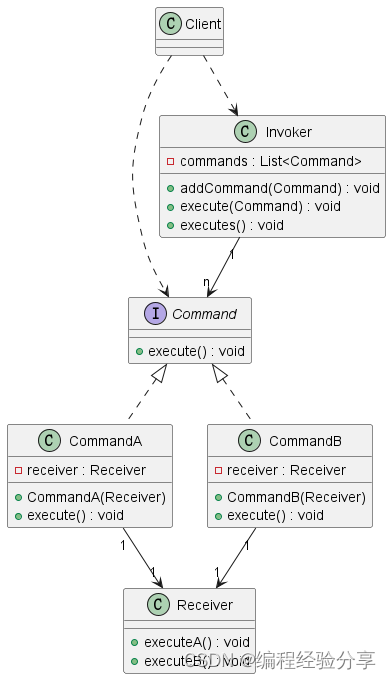
命令模式(请求与具体实现解耦)
目录 前言 UML plantuml 类图 实战代码 模板 Command Invoker Receiver Client 前言 命令模式解耦了命令请求者(Invoker)和命令执行者(receiver),使得 Invoker 不再直接引用 receiver,而是依赖于…...

开发一款MMOARPG难度到底有多大
开发一款MMOARPG难度到底有多大 MMORPG游戏开发到底有多难,我们按照过去开发的标准,就比如开发一款传奇,那时候哪会用什么别人的引擎,都是自研,从基础图形API开始。我们不考虑美术和策划,就单指程序&#x…...
RTSP应用:实现视频流的实时推送
在实现实时视频流推送的项目中,RTSP(Real Time Streaming Protocol)协议扮演着核心角色。本文将指导你通过安装FFmpeg软件,下载并编译live555,以及配置ffmpeg进行视频流推送,来实现一个基本的RTSP流媒体服务…...

Java八股文(数据结构)
Java八股文の数据结构 数据结构 数据结构 请解释以下数据结构的概念:链表、栈、队列和树。 链表是一种线性数据结构,由节点组成,每个节点包含了指向下一个节点的指针; 栈是一种后进先出(LIFO)的数据结构&a…...
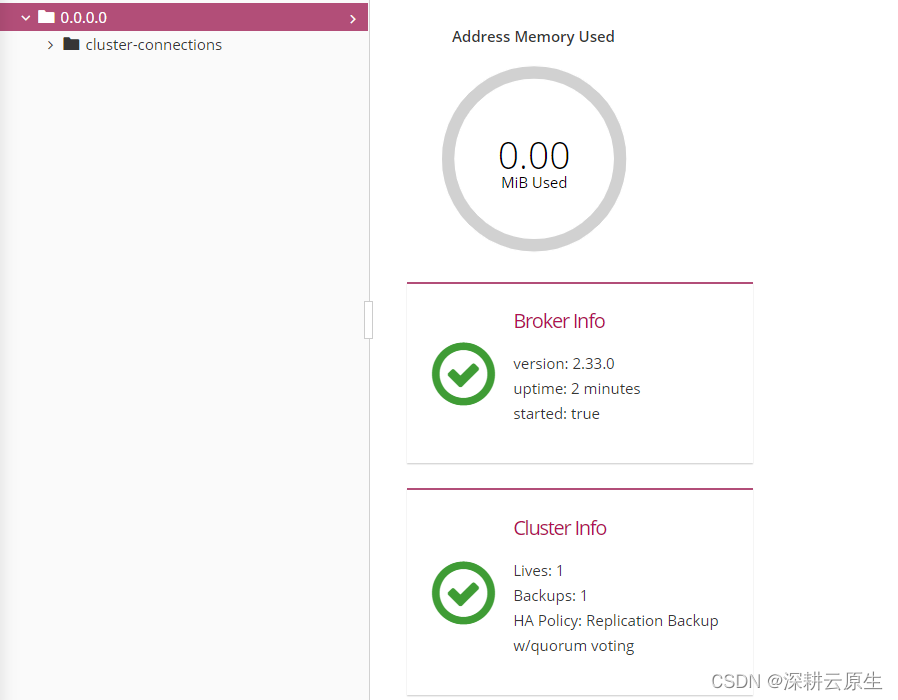
ActiveMQ Artemis 系列| High Availability 主备模式(消息复制) 版本2.19.1
一、ActiveMQ Artemis 介绍 Apache ActiveMQ Artemis 是一个高性能的开源消息代理,它完全符合 Java Message Service (JMS) 2.0 规范,并支持多种通信协议,包括 AMQP、MQTT、STOMP 和 OpenWire 等。ActiveMQ Artemis 由 Apache Software Foun…...

QGIS插件系列--WhiteBox Tools
WhiteBox Tools(官网机翻): WhiteboxTools是由圭尔夫大学地貌测量和水文地理信息学研究小组(GHRG)开发的高级地理空间软件包和数据分析平台。该项目始于2017年<>月,并在分析能力方面迅速发展。WhiteboxTools的一…...
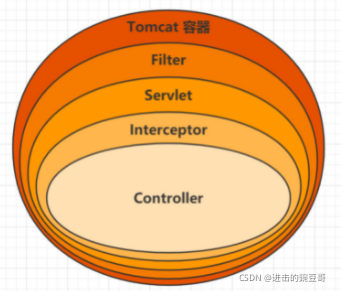
SpringMVC设置全局异常处理器
文章目录 背景分析使用ControllerAdvice(RestControllerAdvice)ExceptionHandler实现全局异常全局异常处理-多个处理器匹配顺序存在一个类中存在不同的类中 对于过滤器和拦截器中的异常,有两种思路可以考虑 背景 在项目中我们有需求做一个全…...

Acwing_795前缀和 【一维前缀和】+【模板】二维前缀和
Acwing_795前缀和 【一维前缀和】 题目: 代码: #include <bits/stdc.h> #define int long long #define INF 0X3f3f3f3f #define endl \n using namespace std; const int N 100010; int arr[N];int n,m; int l,r; signed main(){std::ios::s…...

docker 部署 gitlab-ce 16.9.1
文章目录 [toc]拉取 gitlab-ce 镜像创建 gitlab-ce 持久化目录启停脚本配置配置 gitlab-ce编辑 gitlab-ce 配置文件重启 gitlab-ce配置 root 密码 设置中文 gitlab/gitlab-ce(需要科学上网) 拉取 gitlab-ce 镜像 docker pull gitlab/gitlab-ce:16.9.1-ce.0查看镜像是不是有 Vo…...

29.Python从入门到精通—Python3 面向对象继承 多继承 方法重写 类属性与方法
29.从入门到精通:Python3 面向对象继承 多继承 方法重写 类属性与方法 继承多继承方法重写类属性与方法 继承 在面向对象编程中,继承是指通过继承现有类的属性和方法来创建新类的过程。新类称为子类(或派生类),现有类…...

jQuery如何获取元素宽高?
在jQuery中,获取元素的宽和高有多种方法,取决于你是否需要包括边框、内边距或其他额外空间。以下是几种常用的方式: 获取元素内容区域的宽和高(不包括边框和内边距): var width $(#yourElement).width(); …...
springdata框架对es集成
什么是spring data框架 Spring Data是一个用于简化数据库、非关系型数据库、索引库访问,并支持云服务的开源框架。其主要目标是使得对数据的访问变得方便快捷,并支持 map-reduce框架和云计算数据服务。Spring Data可以极大的简化JPA(Elasticsearch…)的…...
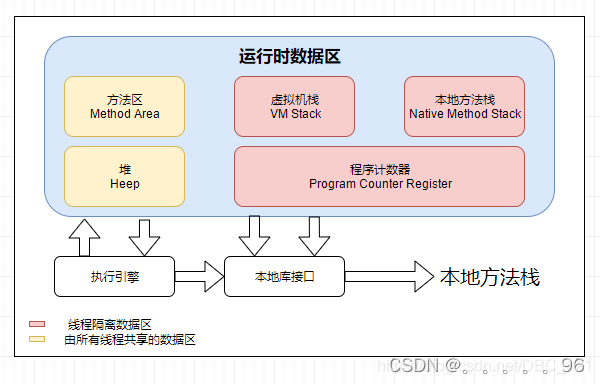
jvm(虚拟机)运行时数据区域介绍
Java虚拟机(JVM)运行时数据区域是Java程序在运行过程中使用的内存区域,它主要包括以下几个部分: 程序计数器(Program Counter Register): 程序计数器是一块较小的内存区域,是线程私有…...
)
C++ MFC 只启动一个程序实例 唤醒之前的实例(完整源码)
初级代码游戏的专栏介绍与文章目录-CSDN博客 很多时候我们希望只允许启动一个程序实例,如果再次运行,就唤醒之前的实例。 目录 1 概述 2 相关技术介绍 2.1 互斥对象 2.2 查找窗口 2.3 唤醒窗口 1 概述 技术上并不难,涉及到以下几个技术…...

2024多云管理平台CMP排名看这里!
随着云计算技术的迅猛发展,多云管理平台CMP应运而生。多云管理平台CMP仅能够简化对多个云环境的统一管理,还能提高资源利用效率和降低成本。因此了解多云管理平台CMP品牌是必要的。2024多云管理平台CMP排名看这里!仅供参考哈! 20…...

MySQL 数据库的日志管理、备份与恢复
一. 数据库备份 1.数据备份的重要性 备份的主要目的是灾难恢复。 在生产环境中,数据的安全性至关重要。 任何数据的丢失都可能产生严重的后果。 造成数据丢失的原因: 程序错误人为,操作错误,运算错误,磁盘故障灾难(如火灾、地震࿰…...
一、Go开发环境搭建
文章目录 1、开发工具2、开发环境配置3、Hello World4、语法 1、开发工具 https://code.visualstudio.com/download 2、开发环境配置 类比Java的JDK,go的SDK下载:https://studygolang.com/dl 解压: 配置环境变量path,将命令&quo…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
