在Isaac-sim中弧度转四元数以及四元数转弧度的问题
问题:
在Isaac-sim中如果采用set_world_pose()和get_world_pose()得到的都是四元数,如何将弧度转四元数,或者将四元数转为弧度是需要解决的一个问题,
这里的弧度是以x轴为0度,y轴为90度,逆时针方向逐渐增大;
解决方案:
采用scipy.spatial.transform中的Rotation库,进行转换;
在转换的时候涉及到角度的变换,
即如果直接采用Rotation.from_euler(‘x’, angle_rad2, degrees=False)进行转换,得到的是以x轴负方向为0度,y轴为90度,顺时针方向逐渐增大;
因此需要在rad_to_quaternion函数中通过angle_rad2 = -angle_rad + math.pi方法进行转换,同样的在quaternion_to_angle函数中通过angle_rad = -angle_rad + math.pi将转换回来。
import math
from scipy.spatial.transform import Rotation
import torchdef rad_to_quaternion(angle_rad):if angle_rad > math.pi:angle_rad -= 2 * math.pielif angle_rad < -math.pi:angle_rad += 2 * math.piangle_rad2 = -angle_rad + math.pirotation = Rotation.from_euler('x', angle_rad2, degrees=False)# print("rotation.as_quat()=%s" % (str(rotation.as_quat())))quaternion = rotation.as_quat()[:] # 将旋转矩阵转换为四元数return quaternion, angle_rad, angle_rad2def quaternion_to_angle(quaternion):rotation = Rotation.from_quat(quaternion)euler_angles = rotation.as_euler('xyz')angle_rad = euler_angles[0]angle_rad = -angle_rad + math.piif angle_rad > math.pi:angle_rad -= 2 * math.pielif angle_rad < -math.pi:angle_rad += 2 * math.pireturn angle_radfor i in range(361):rad = math.radians(i)quaternion, rad_ori, rad_new = rad_to_quaternion(rad)rad_bak = quaternion_to_angle(quaternion)theta0 = math.degrees(rad_ori)theta1 = math.degrees(rad_new)theta2 = math.degrees(rad_bak)print("原始角度为%s,经过变换后角度为%s,转换后的角度为%s"%(str(round(theta0)), str(round(theta1)), str(round(theta2))))# rad_new = math.floor(rad_new * 10000) / 10000# rad_bak = math.floor(rad_bak * 10000) / 10000# if rad_new != rad_bak:# print("出错了rad_new=%s, rad_bak=%s"%(str(rad_new), str(rad_bak)))# print("rad=%.4f, rad_bak=%.4f"%(rad, rad_bak))相关文章:

在Isaac-sim中弧度转四元数以及四元数转弧度的问题
问题: 在Isaac-sim中如果采用set_world_pose()和get_world_pose()得到的都是四元数,如何将弧度转四元数,或者将四元数转为弧度是需要解决的一个问题, 这里的弧度是以x轴为0度,y轴为90度,逆时针方向逐渐增大…...

【计算机网络】高级IO模型
高级IO模型 一、 理解 IO二、认识五种高级 IO 模型1. 阻塞 IO2. 非阻塞IO3. 信号驱动 IO4. IO 多路转接5. 异步 IO 三、高级 IO 重要概念1. 阻塞和非阻塞2. 同步通信和异步通信 四、非阻塞 IOfcntl 一、 理解 IO 当我们调用系统接口 write、read 的时候,本质是把数…...

LabVIEW电动汽车直流充电桩监控系统
LabVIEW电动汽车直流充电桩监控系统 随着电动汽车的普及,充电桩的安全运行成为重要议题。通过集成传感器监测、单片机技术与LabVIEW开发平台,设计了一套电动汽车直流充电桩监控系统,能实时监测充电桩的温度、电压和电流,并进行数…...
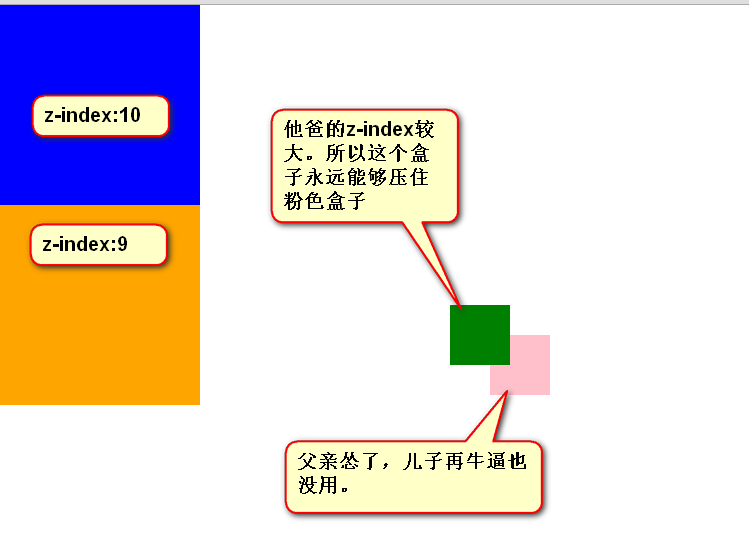
前端学习<二>CSS基础——08-CSS属性:定位属性
CSS的定位属性有三种,分别是绝对定位、相对定位、固定定位。 position: absolute; <!-- 绝对定位 -->position: relative; <!-- 相对定位 -->position: fixed; <!-- 固定定位 --> 下面逐一介绍。 相对定位 相对定位:让…...
)
88. 合并两个有序数组(javascript)
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。 请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。 注意:最终,合并后数组…...

机器学习_集成学习_梯度提升_回归_决策树_XGBoost相关概念
目录 1. 机器学习 使用监督吗?什么又是监督学习? 2. 与XGBoost 类似的机器学习方法有哪些? 3. 随机森林方法 和 梯度提升方法 有什么区别? 分别应用于什么场景? 4. 决策树回归方法 和 Gradient Boosting类回归方法…...
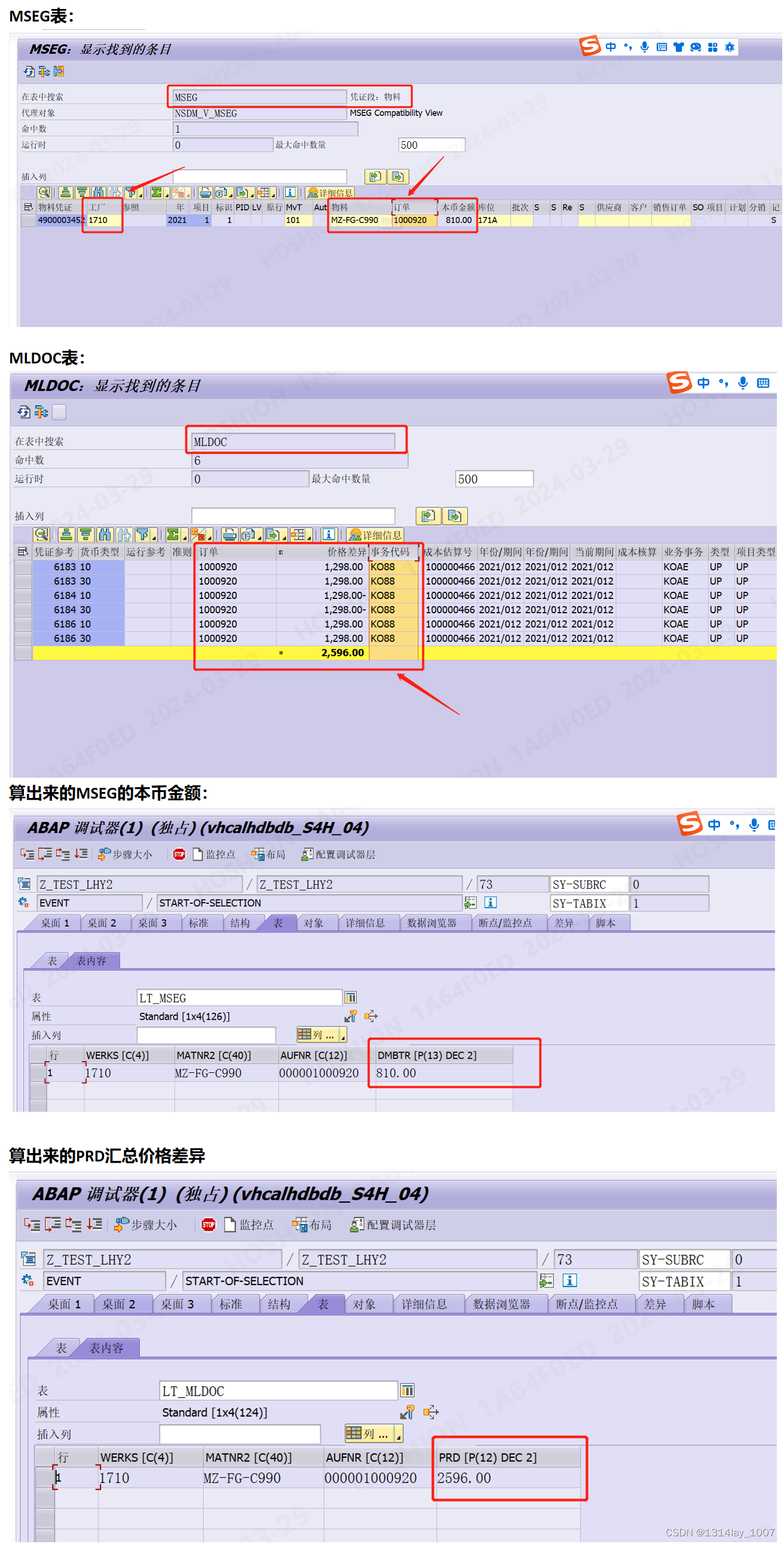
ABAP 字段类型不一样导致相加之后金额错误
文章目录 ABAP 字段类型不一样导致相加之后金额错误写在前面的总结示例程序1汇总MSEG表和MLDOC表 ABAP 字段类型不一样导致相加之后金额错误 写在前面的总结 如果需要不同底表的字段相加的值,那么最好是根据条件去分别算出那些值放在临时内表里面,再去…...

【L1距离和L2距离】Manhattan Distance Euclidean Distance 解释和计算公式
距离度量 特征空间中两个实例点的距离可以反映出两个实力点之间的相似性程度,使用的距离可以是欧式距离,也可以是其他距离。 欧氏距离(L2距离):最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于…...
自动发卡平台源码优化版,支持个人免签支付
源码下载地址:自动发卡平台源码优化版.zip 环境要求: php 8.0 v1.2.6◂ 1.修复店铺共享连接时异常问题 2024-03-13 23:54:20 v1.2.5 1.[新增]用户界面硬币增款扣款操作 2.[新增]前台对接库存信息显示 3.[新增]文件缓存工具类[FileCache] 4.[新增]库存同…...

如何使用固定公网地址远程连接Python编译器并将运行结果返回到Pycharm
文章目录 一、前期准备1. 检查IDE版本是否支持2. 服务器需要开通SSH服务 二、Pycharm本地链接服务器测试1. 配置服务器python解释器 三、使用内网穿透实现异地链接服务器开发1. 服务器安装Cpolar2. 创建远程连接公网地址 四、使用固定TCP地址远程开发 本文主要介绍如何使用Pych…...
Java设计模式—备忘录模式(快照模式)
定义 备忘录模式提供了一种状态恢复的实现机制,使得用户可以方便地回到一个特定的历史步骤,当新的状态无效或者存在问题时,可以使用暂时存储起来的备忘录将状态复原,很多软件都提供了撤销(Undo)操作&#…...
没学数模电可以玩单片机吗?
我们首先来看一下数电模电在单片机中的应用。数电知识在单片机中主要解决各种数字信号的处理、运算,如数制转换、数据运算等。模电知识在单片机中主要解决各种模拟信号的处理问题,如采集光照强度、声音的分贝、温度等模拟信号。而数电、模电的相互转换就…...

FlinkSQL之Flink SQL Join二三事
Flink SQL支持对动态表进行复杂而灵活的连接操作。 为了处理不同的场景,需要多种查询语义,因此有几种不同类型的 Join。默认情况下,joins 的顺序是没有优化的。表的 join 顺序是在 FROM 从句指定的。可以通过把更新频率最低的表放在第一个…...

某某消消乐增加步数漏洞分析
一、漏洞简介 1) 漏洞所属游戏名及基本介绍:某某消消乐,三消游戏,类似爱消除。 2) 漏洞对应游戏版本及平台:某某消消乐Android 1.22.22。 3) 漏洞功能:增加游戏步数。 4…...
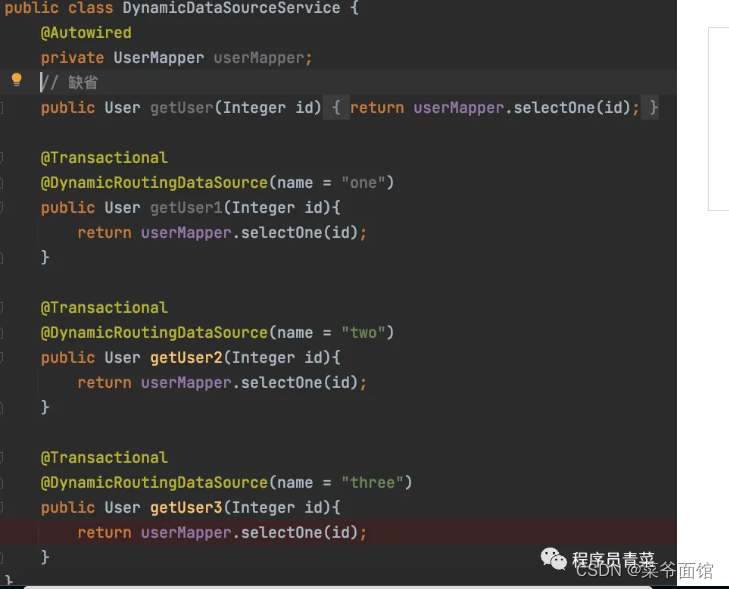
SpringBoot动态数据源实现
一、背景 一个应用难免需要连接多个数据库,像我们系统起码连接了5个以上数据库,AWS RDS主库,ECS自搭MySQL从库,工厂系统三个SQLServer数据库,在线网站MySQL数据库,记得很早以前是用SessionFactory配置&…...

计算机网络常见题(持续更新中~)
1 描述一下HTTP和HTTPS的区别 2 Cookie和Session有什么区别 3 如果没有Cookie,Session还能进行身份验证吗? 4 BOI,NIO,AIO分别是什么 5 Netty的线程模型是怎么样的 6 Netty是什么?和Tomcat有什么区别,特点是什么? 7 TCP的三次…...

富格林:可信招数揭发防备暗箱陷阱
富格林悉知,在风云变幻的金融市场中,炒贵金属是一项具有高收益潜力的投资方式。但投资是风险与收益共存的,因此我们在做单投资过程中需总结可信招数揭发暗箱陷阱,防备受害亏损。以下总结几点可信的投资技巧,希望能够帮…...
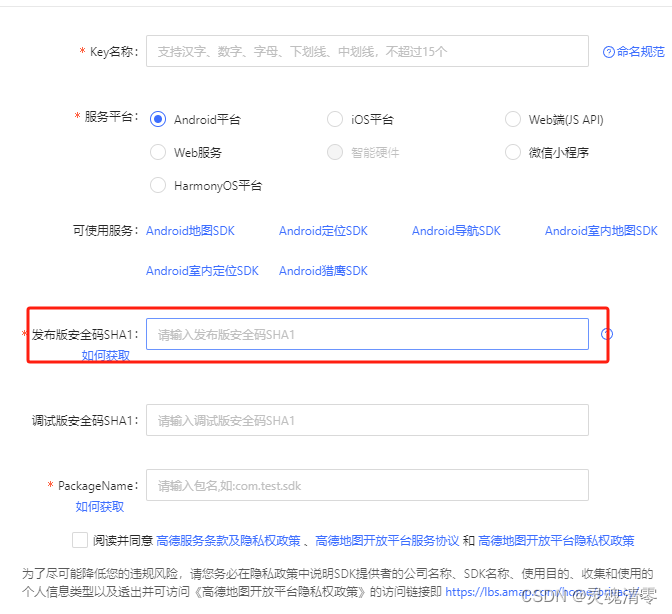
获取高德安全码SHA1
高德开发者平台上给的三种方法 获取安全码SHA1,这里我自己使用的是第三种方法。 1、通过Eclipse编译器获取SHA1 使用 adt 22 以上版本,可以在 eclipse 中直接查看。 Windows:依次在 eclipse 中打开 Window -> Preferances -> Androi…...
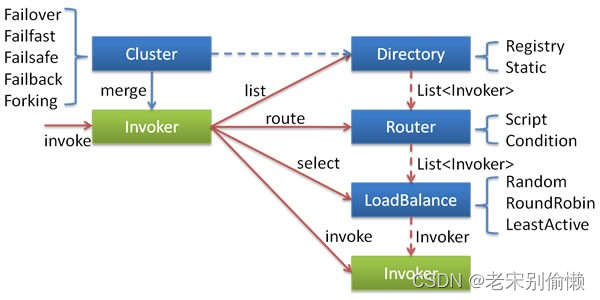
关于RPC
初识RPC RPC VS REST HTTP Dubbo Dubbo 特性: 基于接口动态代理的远程方法调用 Dubbo对开发者屏蔽了底层的调用细节,在实际代码中调用远程服务就像调用一个本地接口类一样方便。这个功能和Fegin很类似,但是Dubbo用起来比Fegin还要简单很多&a…...

pulsar: kafka on pulsar之把pulsar当kafka用
一、下载协议包(要和pulsar版本比较一致) https://github.com/streamnative/kop/releases?q2.8.0&expandedtrue二、在pulsar的根目录创建一个protocols目录,将上述包放到这个目录里 三、编辑broker.conf(如果是集群)或者standalone.con…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
