第14章 局部波动率模型
这学期会时不时更新一下伊曼纽尔·德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思路不一定够清晰且由于分工原因我是从书本第13章写起,还请大家见谅。
第14章 局部波动率模型
股价变动方式的二叉树模型
上一章前瞻波动率 σ(t)\sigma(t)σ(t) 的推导:
∑2(t,T)=1T−t∫tTσ2(s)ds{\sum}^2(t,T)=\frac{1}{T-t}\int_t^T\sigma^2(s)ds ∑2(t,T)=T−t1∫tTσ2(s)ds
σ(t)\sigma(t)σ(t) 会随时间变化而变化,同样地,波动率 σ(S,t)\sigma(S,t)σ(S,t) 也会随未来的时间和股票价格两个参数的变化而变化。
我们将这种瞬时波动率 σ(S,t)\sigma(S,t)σ(S,t) 称为局部波动率,以此为基础建立的模型被称为局部波动率模型。
开发局部波动率模型时需要关注的问题:
- 能否找到独一无二的局部波动率函数或者曲面 σ(S,t)\sigma(S,t)σ(S,t),使其能够描述观察到的隐含波动率曲面 ∑(S,t,K,T)\sum(S,t,K,T)∑(S,t,K,T)?如果可以,这就意味着我们可以用一个股票的局部波动率过程来解释观察到的微笑曲线
- 但是这样的解释是否有意义?股票价格的变动真的会服从这个已经存在的局部波动率函数?我们将会发现,有很多不同的模型都能够描述隐含波动率曲面,但这并不意味着这些模型是“正确的”
- 局部波动率模型如何确定普通期权的对冲比率以及奇异期权的价值?其结论和经典的BSM模型有何差异?
首先,假设我们已经有了一个局部波动率函数,我们在此基础上建立一个二项式局部波动率模型
二项局部波动率模型
假设风险中性条件成立,股票价格 S(t)S(t)S(t) 的变动服从下面的等式:
dSS=(r−b)dt+σ(S,t)dZ\frac{dS}{S}=(r-b)dt+\sigma(S,t)dZ SdS=(r−b)dt+σ(S,t)dZ
其中 r,b,dZ,σ(S,t)r,b,dZ,\sigma(S,t)r,b,dZ,σ(S,t) 分别表示无风险利率、股票的连续股息率、标准维纳过程、局部波动率。在任意时点 ttt,股价变动的方差都满足:
(dS)2=S2σ2(S,t)dt(dS)^2=S^2\sigma^2(S,t)dt (dS)2=S2σ2(S,t)dt
一个瞬时时间段 dtdtdt 之后,SSS 的预期价值等于:
F=Se(r−b)dtF=Se^{(r-b)dt} F=Se(r−b)dt
也即股票的远期价格
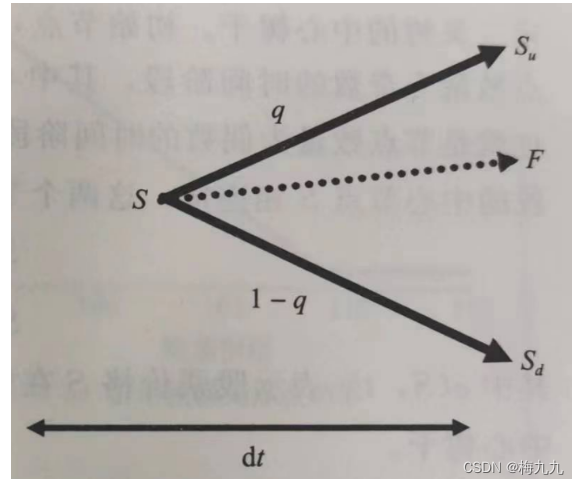
在上述近似二叉树模型中,远期价格就等于 qqq 测度下,两种股票价格 Su,SdS_u,S_dSu,Sd 按照概率加权后的平均值,即:
F=qSu+(1−q)SdF=qS_u+(1-q)S_d F=qSu+(1−q)Sd
求解 qqq:
q=F−SdSu−Sdq=\frac{F-S_d}{S_u-S_d} q=Su−SdF−Sd
SSS 变动值的方差为:
Var[dS]=q(Su−F)2+(1−q)(Sd−F)2Var[dS]=q(S_u-F)^2+(1-q)(S_d-F)^2 Var[dS]=q(Su−F)2+(1−q)(Sd−F)2
当 dt→0dt\to0dt→0 时,(dS)2=S2σ2(S,t)dt(dS)^2=S^2\sigma^2(S,t)dt(dS)2=S2σ2(S,t)dt 与上式相等,可以得到:
S2σ2(S,t)dt=q(Su−F)2+(1−q)(Sd−F)2S^2\sigma^2(S,t)dt=q(S_u-F)^2+(1-q)(S_d-F)^2 S2σ2(S,t)dt=q(Su−F)2+(1−q)(Sd−F)2
将 qqq 的解析式代入得:
S2σ2(S,t)dt=F−SdSu−Sd(Su−F)2+(1−F−SdSu−Sd)(Sd−F)2S2σ2(S,t)dt=F−SdSu−Sd(Su−F)2+(Su−FSu−Sd)(Sd−F)2S2σ2(S,t)dt=(F−Sd)(Su−F)(Su−F−Sd+F)Su−Sd=(F−Sd)(Su−F)S^2\sigma^2(S,t)dt=\frac{F-S_d}{S_u-S_d}(S_u-F)^2+(1-\frac{F-S_d}{S_u-S_d})(S_d-F)^2\\S^2\sigma^2(S,t)dt=\frac{F-S_d}{S_u-S_d}(S_u-F)^2+(\frac{S_u-F}{S_u-S_d})(S_d-F)^2\\S^2\sigma^2(S,t)dt=\frac{(F-S_d)(S_u-F)(S_u-F-S_d+F)}{S_u-S_d}=(F-S_d)(S_u-F) S2σ2(S,t)dt=Su−SdF−Sd(Su−F)2+(1−Su−SdF−Sd)(Sd−F)2S2σ2(S,t)dt=Su−SdF−Sd(Su−F)2+(Su−SdSu−F)(Sd−F)2S2σ2(S,t)dt=Su−Sd(F−Sd)(Su−F)(Su−F−Sd+F)=(F−Sd)(Su−F)
可以得到每个节点 SSS 对应得上行股价和下行股价:
Su=F+S2σ2(S,t)dtF−SdSd=F−S2σ2(S,t)dtSu−FS_u=F+\frac{S^2\sigma^2(S,t)dt}{F-S_d}\\S_d=F-\frac{S^2\sigma^2(S,t)dt}{S_u-F} Su=F+F−SdS2σ2(S,t)dtSd=F−Su−FS2σ2(S,t)dt
只要知道了 S,F,SdS,F,S_dS,F,Sd,根据波动率 σ(S,t)\sigma(S,t)σ(S,t),就可以计算得到 SuS_uSu;同理,知道了 S,F,SuS,F,S_uS,F,Su,就可以计算得到 SdS_dSd
为了增加时间间隔阶段,我们首先需要确定二叉树的中心,接着按照上述所描述的局部波动率曲面,搭建股价上行和下行的树杈。这样就可以得到一个满足所有局部波动率的二叉树。然后,再利用:
q=F−SdSu−Sdq=\frac{F-S_d}{S_u-S_d} q=Su−SdF−Sd
回过头来计算每个节点的风险中性概率。做完这以后,我们就可以用逆向归纳法,沿着二叉树倒推出任何股票衍生品的价格
首先,用上一章中描述的 Cox-Ross-Rubinstein (CRR) 方法来确定二叉树的中心树干。初始节点,也就是树根部位的股票价格为 S0S_0S0,每一个节点数量为奇数的时间阶段,其中心节点 SSS 都等于初始价格 S0S_0S0。其他时间阶段,也就是节点数量为偶数的时间阶段,分布于中心两侧最近的两个节点都与上一阶段的中心节点 SSS 相连接,这两个节点的价格可以表示为
Su=Seσ(S,t)dtSd=Se−σ(S,t)dtS_u=Se^{\sigma(S,t)\sqrt{dt}}\\ S_d=Se^{-\sigma(S,t)\sqrt{dt}} Su=Seσ(S,t)dtSd=Se−σ(S,t)dt
其中 σ(S,t)\sigma(S,t)σ(S,t) 表示股票价格 SSS 在未来时间 ttt 的局部波动率。这种方法明确定义了中心树干。
在每个阶段,从中心节点出发,可以用之前推导出的下式求得上行节点与下行节点:
Su=F+S2σ2(S,t)dtF−SdSd=F−S2σ2(S,t)dtSu−FS_u=F+\frac{S^2\sigma^2(S,t)dt}{F-S_d}\\S_d=F-\frac{S^2\sigma^2(S,t)dt}{S_u-F} Su=F+F−SdS2σ2(S,t)dtSd=F−Su−FS2σ2(S,t)dt
在二叉树中,对于中心树干的初始价格 S0S_0S0 没有明确的要求。比如,我们可以将股票在每个阶段的远期价格确定为中心价格,也可以选择任何其他价格水平。假设在某一阶段,有奇数个节点,股票的远期价格为 FtF_tFt,下一个时间阶段就会有偶数个节点,那么 Su,SdS_u,S_dSu,Sd 就可以改写为:
Su=Fteσ(Ft,t)dtSd=Fte−σ(Ft,t)dtS_u=F_te^{\sigma(F_t,t)\sqrt{dt}}\\ S_d=F_te^{-\sigma(F_t,t)\sqrt{dt}} Su=Fteσ(Ft,t)dtSd=Fte−σ(Ft,t)dt
即确保了在 FtF_tFt 价格下,局部波动率等于 σ(Ft,t)\sigma(F_t,t)σ(Ft,t)
案例:
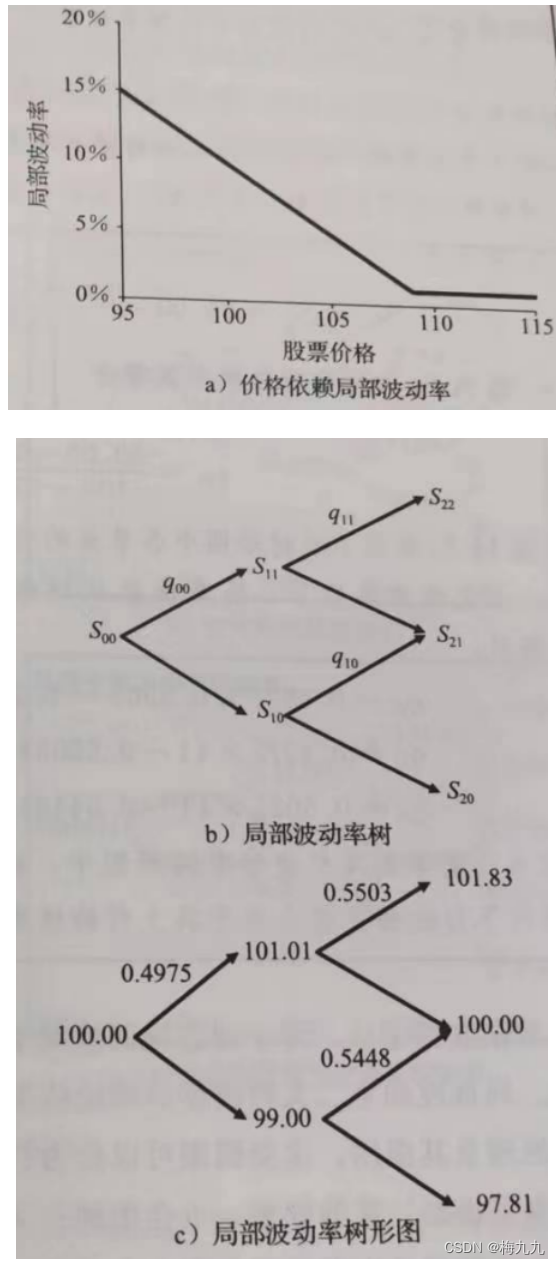
假设某股票当前的价格为 S0=100S_0=100S0=100 美元。假设局部波动率跟未来的时间 ttt 没有关系,只会随着股票价格的变动而变动,二者关系如下:
σ(S)=max[0.1−S−S0S0,0.01]\sigma(S)=\max[0.1-\frac{S-S_0}{S_0},0.01] σ(S)=max[0.1−S0S−S0,0.01]
在当前股票价格水平附近,股票价格每升高 1%,局部波动率就会降低1个百分点。为了保证波动率是正数,我们设定波动率最低等于1%。假设股息率和无风险利率都等于 0。令 Δt=0.01\Delta t=0.01Δt=0.01,建立前三个时间间隔阶段的二叉树模型:
利用标准Cox-Ross-Rubinstein模型可得:
S11=Seσ(S,t)Δt=100e0.10.01=101.01S10=Se−σ(S,t)Δt=100e−0.10.01=99.00S_{11}=Se^{\sigma(S,t)\sqrt{\Delta t}}=100e^{0.1\sqrt{0.01}}=101.01\\ S_{10}=Se^{-\sigma(S,t)\sqrt{\Delta t}}=100e^{-0.1\sqrt{0.01}}=99.00 S11=Seσ(S,t)Δt=100e0.10.01=101.01S10=Se−σ(S,t)Δt=100e−0.10.01=99.00
由于股息率和无风险利率等于0,节点 S00S_{00}S00 的远期价格等于初始价格100美元,股价上行的风险中性概率就等于:
q00=F−SdSu−Sd=100.00−99.00101.01−99.00=0.4975q_{00}=\frac{F-S_d}{S_u-S_d}=\frac{100.00-99.00}{101.01-99.00}=0.4975 q00=Su−SdF−Sd=101.01−99.00100.00−99.00=0.4975
令第三阶段的中心节点 S21S_{21}S21 的价格等于初始价格100美元在节点 S11S_{11}S11 ,局部波动率=0.09,远期价格 F=S11=101.01F=S_{11}=101.01F=S11=101.01,对应下行节点是 S21S_{21}S21,对应上行节点是 S22S_{22}S22,我们有:
S22=F+S112σ2(S11,t)ΔtF−S21=101.01+101.012×0.092×0.01101.01−100=101.83q11=F−S21S22−S21=101.01−100101.83−100=0.5503S_{22}=F+\frac{S_{11}^2\sigma^2(S_{11},t)\Delta t}{F-S_{21}}=101.01+\frac{101.01^2\times0.09^2\times0.01}{101.01-100}=101.83\\ q_{11}=\frac{F-S_{21}}{S_{22}-S_{21}}=\frac{101.01-100}{101.83-100}=0.5503 S22=F+F−S21S112σ2(S11,t)Δt=101.01+101.01−100101.012×0.092×0.01=101.83q11=S22−S21F−S21=101.83−100101.01−100=0.5503
类似的,在节点 S10S_{10}S10 ,局部波动率=0.11,远期价格 F=S10=99.00F=S_{10}=99.00F=S10=99.00,对应下行节点是 S20S_{20}S20,对应上行节点是 S21S_{21}S21,我们有:
S20=F−S102σ2(S10,t)ΔtS21−F=99.00−99.002×0.112×0.01100−99.00=97.81q10=F−S20S21−S20=99.00−97.81100−97.81=0.5448S_{20}=F-\frac{S_{10}^2\sigma^2(S_{10},t)\Delta t}{S_{21}-F}=99.00-\frac{99.00^2\times0.11^2\times0.01}{100-99.00}=97.81\\ q_{10}=\frac{F-S_{20}}{S_{21}-S_{20}}=\frac{99.00-97.81}{100-97.81}=0.5448 S20=F−S21−FS102σ2(S10,t)Δt=99.00−100−99.0099.002×0.112×0.01=97.81q10=S21−S20F−S20=100−97.8199.00−97.81=0.5448
在这个简单的局部波动率树形图中,由于波动率会随着股价的下降而上升,股价下行的幅度就会高于其上行的幅度,因此最终的股价呈现负斜度。
局部波动率与隐含波动率的关系
上述展示了如何建立一个局部波动率树形图。现在需要找到一类局部波动率模型,使其可以用来描述观察到的某特定隐含波动率微笑曲线。
假设继续用上个案例中的二叉树模型,局部波动率函数保持不变,将其扩展到五个时间间隔阶段,得到如下五阶段局部波动率模型二叉树模型
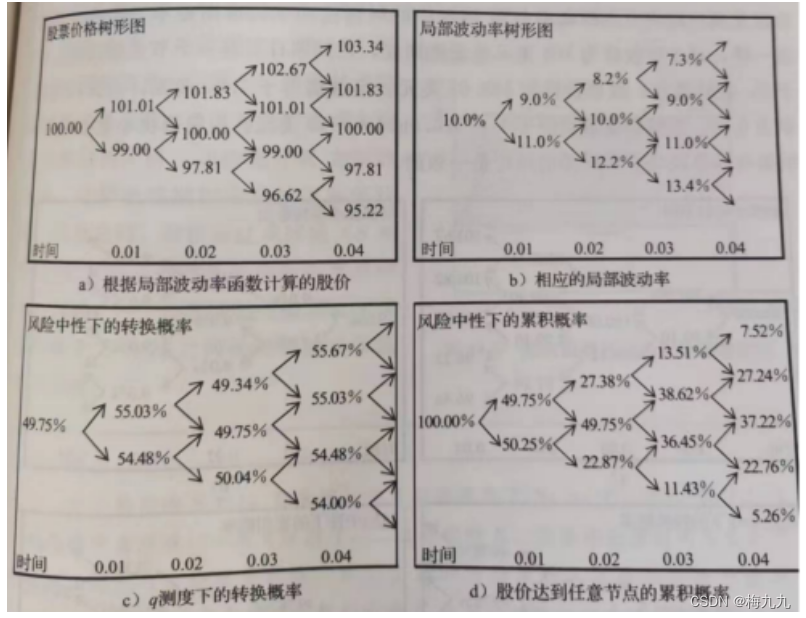
假设有一个欧式看涨期权,行权价为102美元,到期日为5个时间阶段,根据树形图的最终节点,唯一一个在到期日处于实值状态的期权对应的股票价格是103.34美元,此时期权对应的价格是1.34美元。在风险中性条件下,假设无风险利率等于0,那么该期权的现值就是1.34美元。该期权的风险中性预期价值就等于其现值乘以股价到达该节点的累积概率7.52%,即 1.34×0.0752=0.101.34\times0.0752=0.101.34×0.0752=0.10 美元。由于该看涨期权在其他任何一个节点的价值都等于0,因此,0.10美元就是期权在初始时的价值。
另一个角度考虑,股价在到期日高于102美元的风险中性概率又取决于股票在到期日等于实值状态价格之前,股价落在100美元和102美元之间的平均局部波动率水平
根据局部波动率函数,股价在100美元和102美元之间对应的平均局部波动率等于 (10%+8%)/2=9%(10\%+8\%)/2=9\%(10%+8%)/2=9%。可以猜测,在动态局部波动率模型中,行权价为102美元的看涨期权价格,就等于波动率为9%的常数波动率二叉树模型中的价格
为了验证该猜测是否正确,根据CRR方法,建立一个波动率为9%的常数波动率二叉树模型:

对于行权价为102美元的看涨期权,在到期日只有一个节点的损益不等于0,在该节点,股票价格为103.67美元。损益值等于1.67美元,当无风险利率为0时,期权的现值就等于 1.67×0.0614=0.101.67\times0.0614=0.101.67×0.0614=0.10 美元,保留两位小数点之后,结果与局部波动率树形图的结论是一致的。
在常数波动率二叉树模型中,取极限条件,时间间隔趋近于无穷小时,得到的期权价值会收敛至BSM公式的结果
上述案例中,在期权估值时用到的CRR隐含波动率,约等于当前股价水平和期权行权价水平对应的两个局部波动率的线性平均值。对应地,在连续极限条件下,我们推测,正确的BSM隐含波动率约等于股票价格和行权价的两个局部波动率的平均值
为什么这一关系成立?下图展示了不同的股价变动路径。要使最后期权的损益为正数,股价路径就必须上穿过初始股票价格 SSS 和行权价 KKK 之间的区域,这样最终期权才能处于实值状态。在此之前,股价穿过该区域,对应的就是局部波动率的样本。因此,一个标准期权的隐含波动率就约等于 SSS 与 KKK 之间的局部波动率线性平均值

两倍定律:理解局部波动率和隐含波动率之间的关系
期权的隐含波动率 Σ(S,K)\Sigma(S,K)Σ(S,K) 约等于局部波动率 σ(S)\sigma(S)σ(S) 的平均值,这是指在期权有效期内,股价位于当前标的资产价格和行权价之间时的局部波动率。这种关系类似于零息债券,其到期收益率等于远期利率平均值
对于利率而言,正是由于存在这种关系,短端利率的远期值随时间增长的速率是到期收益率增长速率的两倍。与此类似,如果局部波动率函数 σ(S)\sigma(S)σ(S) 只受股价这一个变量的影响,那么我们也可以证明,局部波动率随股票价格变动的速率约等于隐含波动率随行权价格变动速率的两倍。通常,我们将这种关系称为两倍定律。
一个非正式证明:假设一个指数的局部波动率与时间无关,仅与指数价格保持线性关系,于是有:
σ(S)=σ0+βS\sigma(S)=\sigma_0+\beta S σ(S)=σ0+βS
假设有一个处于浅度虚值状态的看涨期权,行权价为 KKK,标的指数的价格水平是 SSS,其隐含波动率表示为 Σ(S,K)\Sigma(S,K)Σ(S,K)。影响期权价值的每一条股价变动路径都将穿过 SSS 和 KKK 之间的区域,如下图所示。这些路径对应的波动率主要是由 SSS 和 KKK 之间的局部波动率决定的。因此,该期权的隐含波动率可以看作等于行权价 KKK 和指数价格水平 SSS 之间的平均局部波动率,也就是图中的阴影部分:

于是:
Σ(S,K)≈1K−S∫SKσ(S′)dS′Σ(S,K)≈1K−S∫SK(σ0+βS′)dS′=1K−S(σ0S′+12βS′2)∣SK=1K−S[σ0(K−S)+12β(K2−S2)]=σ0+β2(K+S)\Sigma(S,K)\approx\frac{1}{K-S}\int_S^K\sigma(S')dS'\\ \Sigma(S,K)\approx\frac{1}{K-S}\int_S^K(\sigma_0+\beta S')dS'\\=\frac{1}{K-S}(\sigma_0S'+\frac{1}{2}\beta S'^2)|_S^K\\=\frac{1}{K-S}[\sigma_0(K-S)+\frac{1}{2}\beta(K^2-S^2)]\\=\sigma_0+\frac{\beta}{2}(K+S) Σ(S,K)≈K−S1∫SKσ(S′)dS′Σ(S,K)≈K−S1∫SK(σ0+βS′)dS′=K−S1(σ0S′+21βS′2)∣SK=K−S1[σ0(K−S)+21β(K2−S2)]=σ0+2β(K+S)
比较 σ(S)=σ0+βS\sigma(S)=\sigma_0+\beta Sσ(S)=σ0+βS 与 Σ(S,K)≈σ0+β2(K+S)\Sigma(S,K)\approx\sigma_0+\dfrac{\beta}{2}(K+S)Σ(S,K)≈σ0+2β(K+S),可以看出,局部波动率随 SSS 变动的速率是隐含波动率随 SSS 变动速率的两倍,同时隐含波动率随 SSS 变动的速率等于其随 KKK 变动的速率
将两式结合可更直观地得到隐含波动率和局部波动率之间的关系:
Σ(S,K)≈σ(S)+β2(K−S)\Sigma(S,K)\approx\sigma(S)+\dfrac{\beta}{2}(K-S) Σ(S,K)≈σ(S)+2β(K−S)
相关文章:

第14章 局部波动率模型
这学期会时不时更新一下伊曼纽尔德曼(Emanuel Derman) 教授与迈克尔B.米勒(Michael B. Miller)的《The Volatility Smile》这本书,本意是协助导师课程需要,发在这里有意的朋友们可以学习一下,思…...

云原生周刊:开源“赢了”,但它可持续吗?
日前召开的 State of Open 会议上,开源“赢了”,但如果政府和企业不站出来确保生态系统在未来的弹性和可持续性,那么它仍然会失败。 OpenUK 首席执行官 Amanda Brock 在开幕式上表示,数字化和开源在过去 5 到 10 年的进步提升了工…...
读《企业IT架构转型之道》
本书还没读完,暂摘抄一些概念,因为自身做的新系统也在转型,从单体式到一体化一年来遇到很多问题有技术上的,也有团队协作的,过程是痛苦且复杂的,所以在刚翻阅前几十页时候,对于淘宝技术团队转型…...
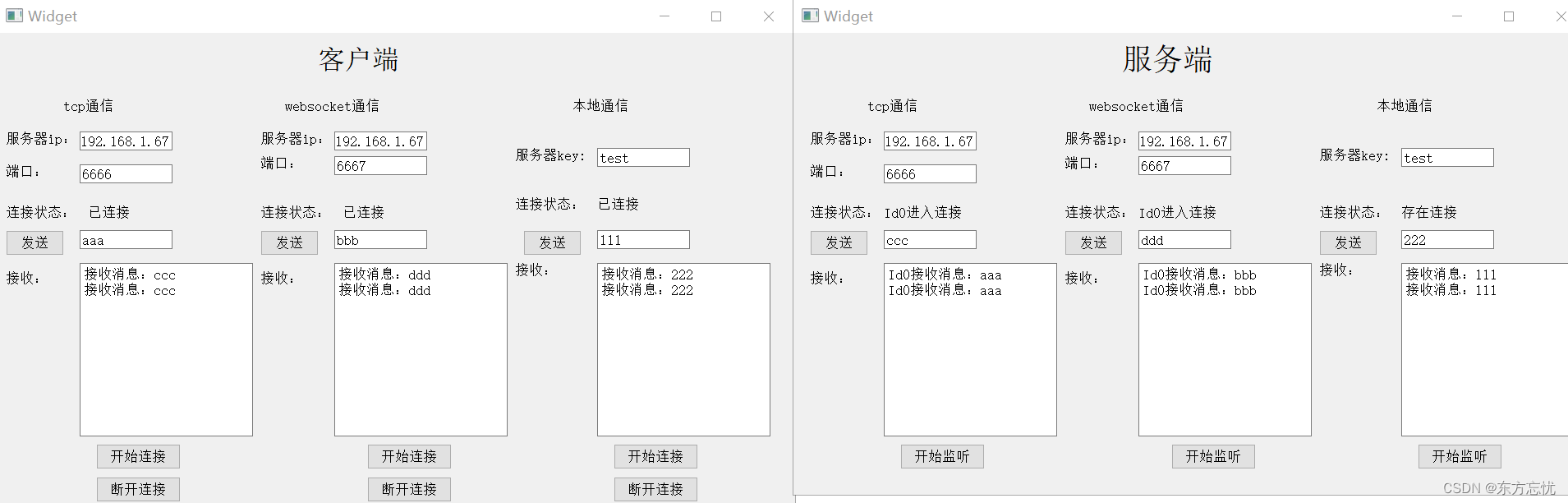
Qt中的QTcpSocket、QWebSocket和QLocalSocket
同时实现了QTcpSocket、QWebSocket和QLocalSocket的简单通讯deamon,支持自动获取本机ip,多个客户端交互。在这个基础上你可以自己加错误检测、心跳发送、包封装解析和客户端自动重连等功能。 获取本机电脑ip: QString Widget::getIp() {QSt…...

枚举学习贴
1. 概述 1.1 是什么 枚举对应英文(enumeration, 简写 enum)枚举是一组常量的集合。可以这里理解:枚举属于一种特殊的类,里面只包含一组有限的特定的对象 1.2 枚举的二种实现方式 自定义类实现枚举使用 enum 关键字实现枚举 1.3 什么时候用 存在有限…...
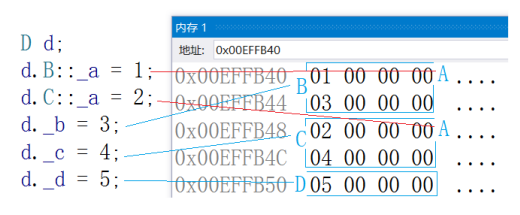
【C++】30h速成C++从入门到精通(继承)
继承的概念及定义继承的概念继承(inheritance)机制是面向对象程序设计使代码可以复用的重要手段,它允许程序员在保持原有类特性的基础上进行扩展,增加功能,这样产生新的类,称派生类。继承呈现了面向对象程序…...

Java多线程还不会的进来吧,为你量身打造
💗推荐阅读文章💗 🌸JavaSE系列🌸👉1️⃣《JavaSE系列教程》🌺MySQL系列🌺👉2️⃣《MySQL系列教程》🍀JavaWeb系列🍀👉3️⃣《JavaWeb系列教程》…...

8 神经网络及Python实现
1 人工神经网络的历史 1.1 生物模型 1943年,心理学家W.S.McCulloch和数理逻辑学家W.Pitts基于神经元的生理特征,建立了单个神经元的数学模型(MP模型)。 1.2 数学模型 ykφ(∑i1mωkixibk)φ(WkTXb)y_{k}\varphi\left(\sum_{i1…...
使用QIS(Quantum Image Sensor)图像重建总结(1)
最近看了不少使用QIS重建图像的文章,觉得比较完整详细的还是Abhiram Gnanasambandam的博士论文:https://hammer.purdue.edu/articles/thesis/Computer_vision_at_low_light/20057081 1 介绍 讲述了又墨子的小孔成像原理,到交卷相机…...
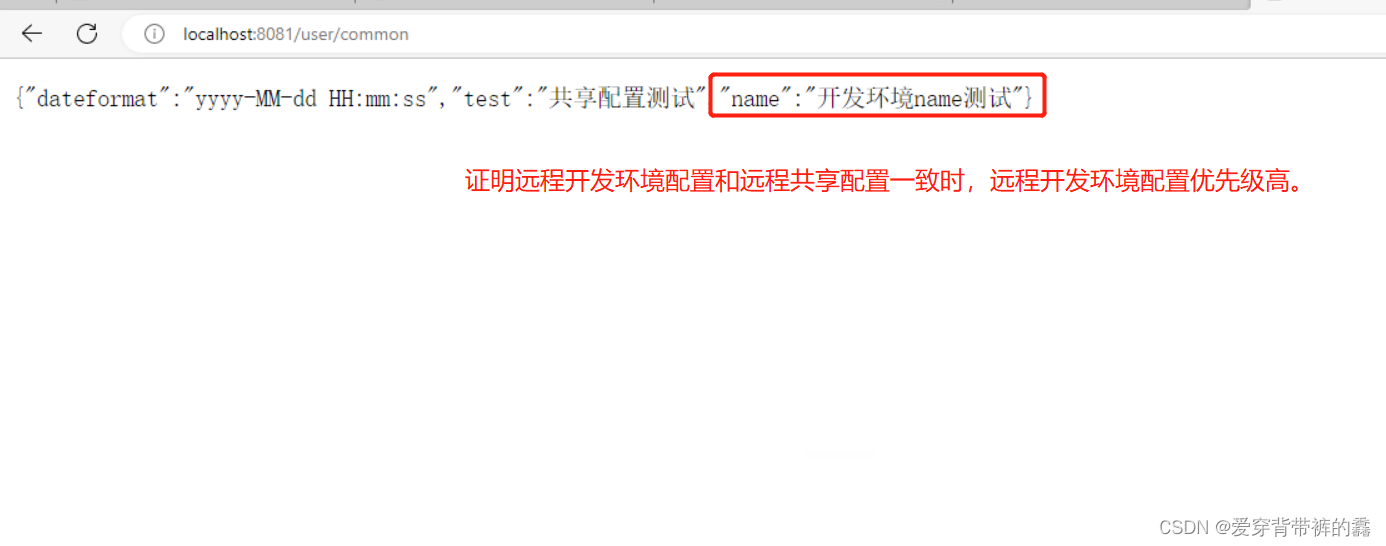
【SpringCloud】SpringCloud教程之Nacos实战(二)
目录前言一.Nacos实现配置管理二.Nacos拉取配置三.Nacos配置热更新(自动刷新,不需要重启服务)1.在有Value注入变量所在类添加注解2.新建类用于属性加载和配置热更新四.Nacos多环境配置共享1.多环境共享配置2.配置的加载优先级测试3.配置优先级前言 Nacos实战一&…...

利用Qemu工具仿真ARM64平台
Windows系统利用Qemu仿真ARM64平台0 写在最前1 Windows安装Qemu1.1 下载Qemu1.2 安装Qemu1.3 添加环境变量1.4测试安装是否成功2. Qemu安装Ubuntu-Server-Arm-642.1 安装前的准备2.2 安装Ubuntu server arm 64位镜像3 Windows配置Qemu网络和传输文件3.1 参考内容3.2 Windows安装…...
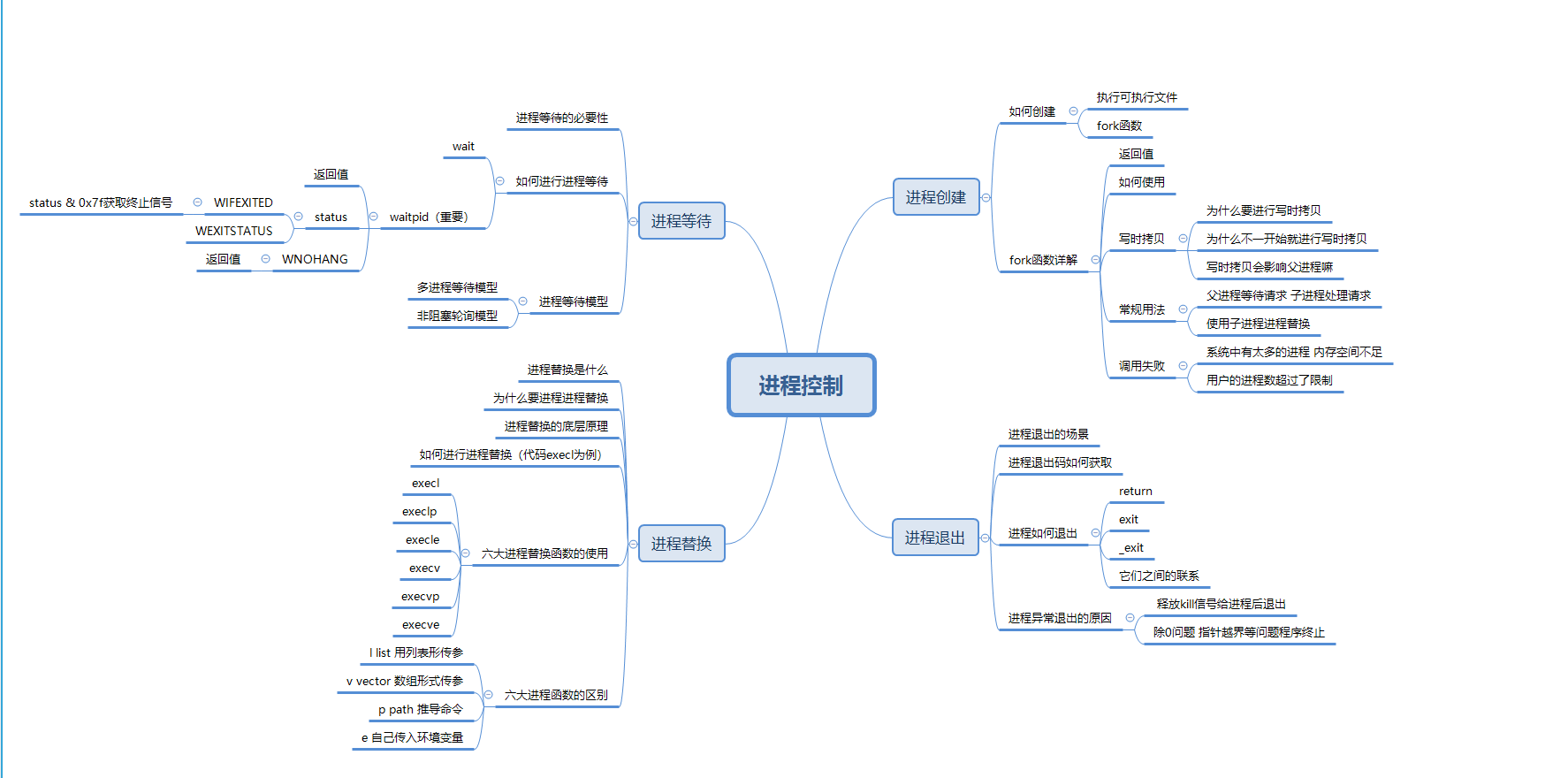
【Hello Linux】进程控制 (内含思维导图)
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:简单介绍下进程的控制 包括进程启动 进程终止 进程等待 进程替换等概念 进程控制介绍进程创建fork函数fork函数的返回值fork函数的使用…...

嵌入式linux物联网毕业设计项目智能语音识别基于stm32mp157开发板
stm32mp157开发板FS-MP1A是华清远见自主研发的一款高品质、高性价比的Linux单片机二合一的嵌入式教学级开发板。开发板搭载ST的STM32MP157高性能微处理器,集成2个Cortex-A7核和1个Cortex-M4 核,A7核上可以跑Linux操作系统,M4核上可以跑FreeRT…...
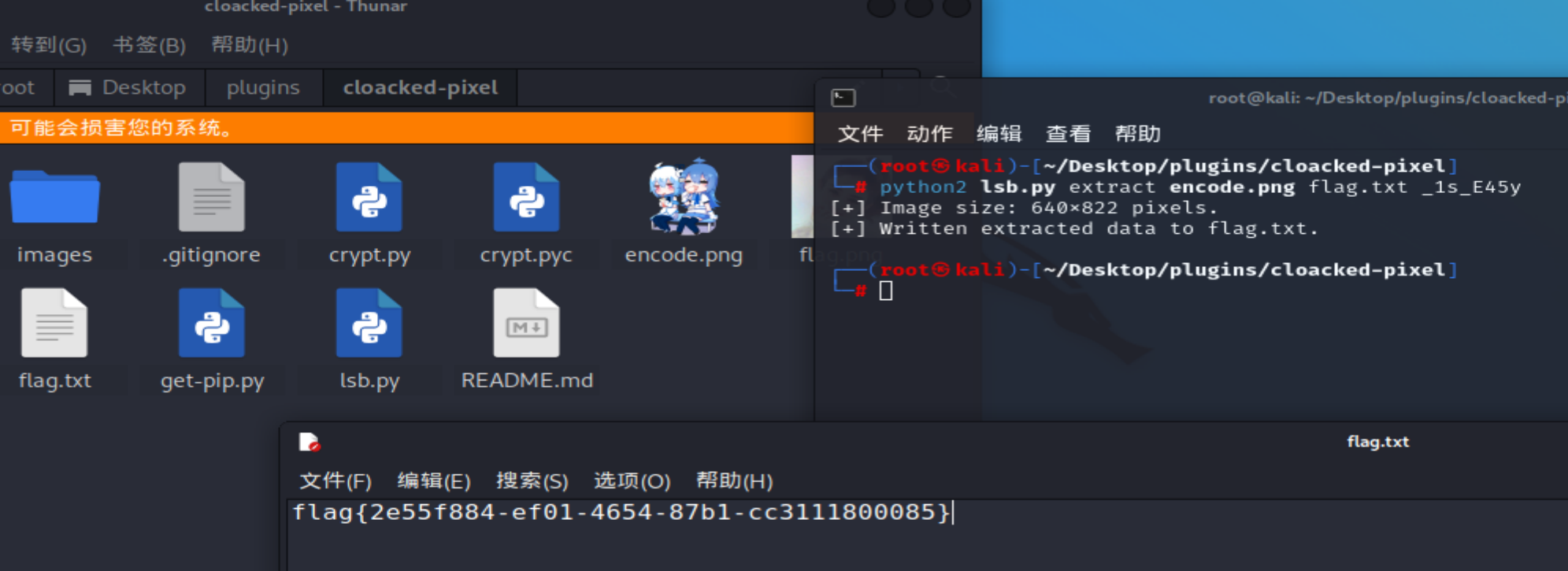
【黄河流域公安院校网络空间安全技能挑战赛】部分wp
文章目录webbabyPHPfunnyPHPEzphp**遍历文件目录的类**1、DirectoryIterator:2、FilesystemIterator:3、**Globlterator**读取文件内容的类:SplFileObjectMisc套娃web babyPHP <?php highlight_file(__FILE__); error_reporting(0);$num $_GET[nu…...

五点CRM系统核心功能是什么
很多企业已经把CRM客户管理系统纳入信息化建设首选,用于提升核心竞争力,改善企业市场、销售、服务、渠道和客户管理等几个方面,并进行创新或转型。CRM系统战略的五个关键要点是:挖掘潜在客户、评估和培育、跟进并成交、分析并提高…...
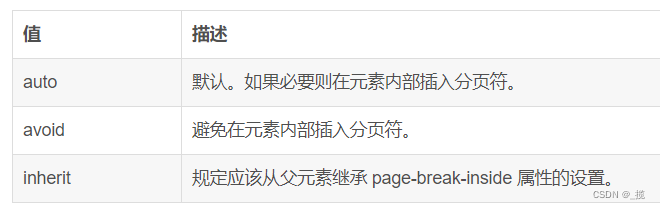
window.print() 前端实现网页打印详解
目录 前言 一、print()方法 二、打印样式 2.1使用打印样式表 2.2使用媒介查询 2.3内联样式使用media属性 2.4在css中使用import引入打印样式表 三、打印指定区域部分内容 3.1方法一 3.2方法二 3.3方法三 四、强制插入分页 4.1page-break-before(指定元素前…...

php程序员应具有的7种能力
php程序员应具有什么样的能力,才能更好的完成工作,才会有更好的发展方向呢?在中国我想您不会写一辈子代码的,那样不可能,过了黄金期,您又怎么办呢?看了本文后,希望对您有所帮助。 一…...
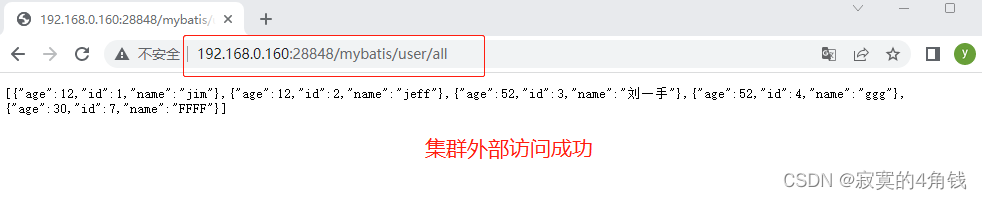
quarkus 生产环境与k8s集成总结
quarkus 生产环境与k8s集成总结 大纲 基础准备quarkus2.13.7脚手架工程配置GraalVM-java11 安装配置配置maven3.8.7linux环境下云原生二进制文件打包环境搭建编译运行quarkus二进制文件quarkus二进制文件制作为docker镜像并运行使用k8s部署quarkus二进制文件 基础准备 生产…...
蓝桥杯训练day2
day21.二分(1)789. 数的范围(2)四平方和(1)哈希表做法(2)二分做法(3)1227. 分巧克力(4)113. 特殊排序(5)1460. 我在哪?2.双指针(1)1238. 日志统计(2)1240. 完全二叉树的权值(3&#…...

为什么99%的程序员都做不好SQL优化?
连接层 最上层是一些客户端和链接服务,包含本地sock 通信和大多数基于客户端/服务端工具实现的类似于 TCP/IP的通信。主要完成一些类似于连接处理、授权认证、及相关的安全方案。在该层上引入了线程 池的概念,为通过认证安全接入的客户端提供线程。同样…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...