论文阅读,The Lattice Boltzmann Method: Principles and Practice(六)(1)
目录
一、流体模拟方法概述
2.1 有限差分
2.2 有限体积法
2.3 有限元法
三、基于粒子的求解器
3.1 动力学理论
3.2 分子动力学
3.3 格子气体模型
3.4 耗散粒子动力学
3.5 多粒子碰撞动力学
3.6 直接模拟蒙特卡罗方法
3.7 平滑粒子流体动力学
四、Why Lattice Boltzmann?
4.1 LBM与其他方法的对比
4.2 LBM的局限性
五、总结
本书主要是介绍LBM的基本原理,还包括了如何将其应用于实际模拟。LBM发展于1980年的晶格气体模型,并在这几十年来稳步增长。由于LBM的简单性、可并行性、在并行计算机上的可拓展性,吸引着世界各地的研究人员。
作者提到了一些使用LBM但书中未详细讨论的系统模拟案例,如湍流、相分离、多孔介质中的流动、跨声速和超音速流动、非牛顿流体力学、稀薄气体流动、微观和纳米流体力学、相对论性流动、磁流体力学和电磁波传播等。(是不是意味着LBM本身是可以用到这些领域的)。
本书我看完目录之后还是很惊喜的,有个问答环节,你感兴趣的问题可以快速在此找到对应的章节(答案),先列一下我感兴趣或者比较关键的几个问题:
- 比对一下NS方程,LBM或者其他常见的CFD算法的优缺点,应用领域,应用空间,弄明白分类依据,对CFD的大分类还是有点凌乱,评估好应用潜力才知道对其加速是否值得或必要;
- 格子可伸缩性对硬件平台的影响,因为LBM的格子大小不像有限体积法,可以在同一个mesh有不同尺度的格子,那么在格子变大变小后,在同一个硬件平台上是否需要从头计算?
看完QA列表后,感兴趣的一些问题:
- 如何尽可能快的了解LBM的基础?阅读顺序:3.2->3.3->5.1->6.1
- 什么是lattice(格子),如何选择一个好的格子?见3.4.7
- 如何在物理单元和模拟的“晶格”单元之间进行转换?见7.1
- 如何选择模拟的参数?见7.2
- 什么时候LBM是求解Navier-Stokes方程的好选择?见2.4
- 玻尔兹曼方程的基础是什么?见1.3
- 如何证明格玻尔兹曼方程可以用来模拟NS方程?见4.1
- 如果代码运行慢的话,如何加速它?见第13章
具体来说,流体动力学关注的是流体运动的宏观现象,其将流体视作连续的物质团(连续体),即是一种连续介质的描述方法,描述宏观流体的行为。但这种方法忽略了流体也是有分子组成的事实,即可用微观分子动力学的理论开描述流体分子在整个空间的分布演化。
简单来说,针对流体的运动可以从微观、介观、宏观三种角度进行描述,微观描述由牛顿动力学控制,表示分子层面的描述;宏观描述由NS平衡方程控制,表现为完全连续的图像(fully continuum picture,这个说法好迷),比如流体的密度和速度;介观则是介于二者之间,即不追踪单个分子,而是追踪分子或分子团的分布。
本篇博客先主要关注CFD算法的分类,优缺点,及应用场景。
一、流体模拟方法概述
尽管有些流体力学方程看起来相对简单,但它们的解的行为非常复杂,以至于只有在某些特定情况下和对于少数几何形状才能得到解析解。方程的非线性特性和复杂形状的边界条件使得找到解析解变得极其困难,甚至是不可能的。因此,大多数情况下需要在计算机上数值求解流体力学方程以获得流场。流体模拟的方法大致可以分为两大类:
- 首先,基于离散化流体力学方程的传统数值方法,如有限差分法、有限体积法和有限元法。比如,传统的Navier-Stokes求解器,属于“自顶向下”的方法,直接对宏观流体方程进行离散化求解。这些方法通常基于宏观流体动力学方程,如Navier-Stokes方程,并通过通用的数值方法(如有限差分法、有限元法或谱方法)进行求解。
- 第二,基于微观、介观或宏观粒子的方法,如分子动力学、晶格气体模型和多粒子碰撞动力学。这些方法通常属于“自底向上”的方法,这些方法从流体的微观粒子相互作用出发,通过模拟大量粒子的行为来推断宏观流体的性质。例如,平滑粒子流体动力学(SPH)和分子动力学模拟都属于这一类方法。其次,我们关注的重点,LBM方法也属于基于粒子的方法类别,因为它从微观层面上的粒子分布函数出发,通过模拟粒子在格子上的碰撞和流动来计算宏观流体的行为。
二、传统的Navier-Stokes求解器
数值方法的工作原理:传统的数值方法通过将感兴趣的方程或方程组进行直接求解(如何选取方程组,应该是感觉实际的物理问题和条件),使用特定的近似方法对其直接进行求解。在CFD中,需要求解的基本方程是连续性方程和Navier-Stokes方程(或它们的不可压缩形式)。根据模拟的物理过程和所使用的近似,可能会增加额外的方程,如能量方程和状态方程。
方程的离散化:为了在计算机上近似求解这些方程,方程中的导数总是以某种形式被离散化。传统的CFD方法通过它们用于离散化解决方案的不同方式来区分,即它们如何使用有限的数字集合来表示连续物理空间中的解。接下来简要介绍一些基础方法的基础知识,即有限差分法、有限体积法和有限元法。(不会介绍边界元方法(BEM),常用于复杂几何形状中的缓慢流动,也不会涵盖流体动力学的谱方法)
2.1 有限差分
有限差分法(FD)是一种数值分析技术,通过函数在一系列离散点上的值来近似求解微分方程。其主要原理目前不是我们关注的重点,了解一下他的优缺点,如下:
- 简单有效:在原理上,这种方法相对简单且有效,适用于一些简单的方程,实际操作中也不是特别困难,但需要注意维持方案的稳定性和一致性。
- 特殊技术要求:由于流体方程的复杂性,使用FD方法解决CFD问题需要采用一些特殊技术,这增加了实现基于FD CFD求解器的难度。
- 非守恒性:有限差分还有可能是不守恒的,意味着数值误差会导致如质量、动量和能量等量的守恒不被完美遵守。比如,在纯平流情况下,即理论上不应该有扩散的情况下,平流型FD方案可能因数值误差而导致被平流的量发生扩散,这被称为假扩散。
- 复杂几何问题:由于FD方法基于规则网格,它难以处理不符合网格的复杂几何形状。虽然原则上可以在不规则网格上应用FD,但实际上这种做法很少使用。
2.2 有限体积法
在有限体积(FV)法中,空间不需要划分为规则网格。相反,将模拟的体积V细分为许多更小的体积Vi,这些体积Vi彼此之间可能有不同的大小和形状。这比有限差分法可以更好地表示复杂的几何图形,如图2.5所示。在每个有限体积Vi的中间,有一个节点,其中每个解变量用其在该体积内的近似平均值表示。
-
保守性和灵活性:FV方法的控制体积公式使其在本质上是保守的,例如在封闭系统的整个域中,意味着质量和动量总是完全守恒的。此外,FV方法非常适合用于不规则网格,它可以很好地捕捉复杂的几何形状,并且可以在模拟的关键区域细化网格,来“投入”更多的分辨率。
-
不规则网格的挑战:尽管不规则网格为模拟复杂几何提供了灵活性,但为复杂几何创建合适的网格本身是一个相当复杂的问题。此外,处理高阶FV方法,特别是在三维和不规则网格中,并不简单。
适用范围:FV方法是用来求解守恒方程的,尽管FV方法在可以解决的方程类型上不如FD方法通用(FD方法原则上可以用于任何方程),但对于CFD中遇到的方程来说,这通常不是问题。
2.3 有限元法
有限元方法(FEM)是解决偏微分方程(PDEs)的另一种数学技术,它使用积分形式,称为弱形式,来解决问题。在FEM中,偏微分方程乘以权重函数 w(x)w(x) 并在感兴趣的领域上积分,这就是所谓的弱形式。
-
FEM的优点:FEM的主要优点是它在数学上非常适合非结构化网格,并且通过使用高阶基函数可以提高精度。这些网格可以动态调整,以适应动态几何形状的变化,如模拟汽车碰撞。
-
FEM的缺点:与FD方法一样,FEM在默认情况下不是保守的,这与FV方法不同。FEM相对于FD和FV方法在复杂性上也有不利之处,特别是在处理一般非结构化网格上的积分时。解决如Navier-Stokes方程这样的复杂系统也不是直接的。
总之,有限元方法在处理非结构化网格和提高解的精度方面具有显著优势,但同时也面临一些挑战,如非保守性和处理复杂度较高。与FD和FV方法相比,FEM在解决特定类型的CFD问题时提供了独特的优势和考虑因素。
三、基于粒子的求解器
基于粒子的求解器,它们不是直接对流体力学方程进行离散化,而是通过模拟大量粒子的运动和相互作用来间接解决流体问题。根据该方法,粒子可以表示例如原子、分子、分子的集合或宏观流体的一部分。因此,传统的Navier-Stokes求解器采用流体的完全宏观观点,而基于粒子的方法通常采用微观或介观观点。在本节中,我们简要介绍六种不同的基于粒子的方法,大致从微观,介观,到宏观。
3.1 动力学理论
动力学理论旨在描述粒子系统的运动和相互作用。在气体和流体中,粒子(如原子、分子)之间的碰撞是系统动力学行为的重要组成部分。而碰撞算子提供了一种数学工具,用于描述这些碰撞事件对粒子速度分布函数的影响。
虽然动力学理论在原则上可以用来描述任何流体,但它通常适用于稀疏气体(dilute gas)的最简单的情况。在那里,假设组成分子实际上的碰撞花费的时间很少。这相当于假设分子几乎总是一对一地发生碰撞,而三个粒子几乎从未同时参与过碰撞。这种假设不适用于致密气体(dense gas),因为分子离得更近,因此花费更多的时间碰撞;而对于液体,因为分子被分子间吸引,从而不断相互作用,则根本不成立。因此建立液体动力学的理论比稀疏气体动力学难得多。气体的动力学理论可以被视为完全的经典物理学,因为它是对大量粒子的统计描述。根据玻尔的对应原理(百度百科_波尔对应原理),当系统足够大时,系统的量子行为会退化为经典行为。
即,动力学理论关注系统随时间的演化。碰撞算子描述了在局部区域内,由于粒子碰撞而导致的分布函数的变化(粒子层面的行为),从而推动系统向平衡状态的演化(宏观现象和性质)。
而一个有用的碰撞算子必须尊重守恒定律,即在碰撞过程中保持系统的总质量、动量和能量不变。玻尔兹曼的原始碰撞算子是速度空间上一个复杂而繁琐的二重积分的形式。它考虑了任何分子间力选择的双粒子碰撞的所有可能结果。然而,在LBM中使用的碰撞算子通常是基于要简单得多的BGK碰撞算子。
-
Boltzmann碰撞算子:Boltzmann的原始碰撞算子是一个非常复杂且难以处理的二重积分,它涉及到速度空间中的所有可能的两粒子碰撞结果。这个算子考虑了分子间作用力的所有可能选择,并且能够详细地描述粒子之间的碰撞过程。然而,由于其复杂性,这个算子在实际应用中往往难以直接使用。
-
BGK碰撞算子:与Boltzmann算子相比,LBM(格子玻尔兹曼方法)中使用的碰撞算子通常基于更简单的BGK模型。BGK模型是一个单积分表达式,它近似地描述了碰撞过程,并且简化了计算。BGK算子假设碰撞后的分布函数是局部平衡分布函数的线性偏差,并且通过一个单一的松弛时间来描述系统从非平衡状态向平衡状态的过渡。
尽管BGK算子在描述复杂的分子间作用力和碰撞过程方面不如Boltzmann算子精确,但它的简单性使得在计算流体动力学和LBM中更容易实现和计算。这种简化在多数情况下都能够提供足够准确的结果,尤其是在处理宏观流体动力学问题时。
3.2 分子动力学
分子动力学(Molecular Dynamics,MD)是一种微观方法,主要用于跟踪代表原子或分子的粒子的位置。这些粒子通过相互作用力进行交互,这些力被选定以尽可能接近实际物理力。通过知道作用于第i个粒子的总力 fi,可以根据牛顿第二定律计算其加速度,并进一步更新粒子的位置。
Verlet算法:在MD中,粒子位置的更新可以通过数值积分牛顿运动方程来实现。Verlet算法是一种简单而有效的积分算法,它利用粒子的当前位置和先前位置来预测其下一个位置。Verlet方案也可以等效地用粒子的速度而不是其先前位置来表达。
MD方法的局限性:虽然MD是模拟微观现象(如化学反应、蛋白质折叠和相变)的强大方法,但由于其跟踪单个分子的高细节程度,将其用于宏观现象是极不实际的(计算成本和复杂性的限制)。举个例子,考虑一克水中含有超过 10^22个分子,MD作为Navier-Stokes求解器的效率极低,因此对于宏观流体动力学问题,需要选择更合适的方法。
3.3 格子气体模型
HPP模型:格子气体模型(Lattice Gas Model)是一种通过模拟粒子在格子上的移动和相互碰撞来重现流体宏观行为的粒子方法,介观尺度,于1973年提出,称为HPP模型。在这个模型中,虚拟的粒子存在于一个正方形晶格上,以质量和动量的守恒的方式向前流动(stream)和碰撞(collide)。由于是正方形,每个节点都有四个邻居,即每个粒子都有四种可能的速度中的一种,在一个时间步内将一个粒子带到一个相邻的节点。这种模型也是格子Boltzmann方法(LBM)的前身。
FHP模型:格子气体模型的一个重要发展是于1986年提出的FHP模型,它改进了原始的HPP模型,引入了三角格子和六个可能的速度,从而提供了足够的格子各向同性以进行流体模拟。各向同性指的是模型在各个方向上的物理特性(如速度,密度等)是相同的。
大致算法:在格子气体模型中,每个格点上的粒子都有一个速度,粒子的存在与否由占据数(occupation number)表示,它是一个布尔变量,取值为0或1,分别表示粒子的不在和在。这个占据数可以直接用来确定宏观观测量,如格点的质量密度和动量密度。格子气体模型的时间演化遵循两条规则:碰撞和流动。在碰撞规则中,相遇在同一格点的粒子可能会以保持该点质量和动量守恒的方式重新分布。碰撞可以用数学表达式来表示,该表达式会基于该节点所有的占据数进行粒子的重新分布。
格子气体模型的优点:
-
布尔变量:格子气体模型中的占据数是布尔变量,表示粒子在特定格点上的存在与否(即粒子要么存在要么不存在),这样的处理方式使得碰撞处理在理论上是完美无误的,因为它避免了在其他CFD方法中使用浮点运算所固有的舍入误差。
-
可并行化:由于其简单的布尔运算,格子气体模型非常适合大规模并行计算,这可以显著提高计算效率。
格子气体模型的局限性:
-
碰撞处理的复杂性:当速度的数量增加时,处理碰撞变得非常复杂。例如,在具有24个速度的三维格子气体模型中,一个格点可能有 2^24(约1680万)种可能的状态。碰撞的解决通常需要通过查找一个由专门程序生成的巨大表格来实现,这使得模型变得非常复杂。
-
各向同性问题:FHP模型在Navier-Stokes方程的各向同性方面存在问题,这些问题只有在低马赫数(即准不可压缩流动)的情况下才能消失。
-
雷诺数的限制:与其他CFD方法相比,格子气体模型难以达到很高的雷诺数(Reynolds number),这限制了它们在模拟高速或湍流流动时的应用。
-
统计噪声:像真实气体一样,格子气体在微观水平上充满了活动,导致即使在平衡状态下,宏观量(如密度和流速)也会出现波动。尽管通过时空平均或多个系综平均可以部分减少这种噪声,但总会有一些噪声残留。这种统计噪声对于模拟宏观流体来说是一种干扰。
由于上述限制,特别是统计噪声的问题,格子Boltzmann方法(Lattice Boltzmann Method, LBM)在20世纪80年代末被提出,作为格子气体模型的改进。LBM通过跟踪占据数的期望值而不是占据数本身(不再关注单个粒子是否存在于特定的格点和方向上,而是关注在这个格点和方向上粒子出现的平均概率),这种处理方式相当于从微观粒子的随机运动中提取出了平均行为,从而在宏观层面上得到了更平滑、无噪声的流体流动描述,且不受微观层面随机波动的干扰,从而消除了统计噪声。最初,人们并不完全理解如何从气体动理论导出LBM,直到90年代中期,这一方法的更现代的导出方式才被发展出来。
tips:雷诺数是流体动力学中的一个无量纲数,表示惯性力与粘性力的比率,用于区分流动是层流(低雷诺数)还是湍流(高雷诺数)。高雷诺数流通常以湍流为主,并与车辆空气动力学、建筑设计和许多其他应用有关。另一方面,低雷诺数流在微流体和生物物理学中具有重要作用。
3.4 耗散粒子动力学
耗散粒子动力学(Dissipative Particle Dynamics, DPD)是一种介观尺度上的模拟方法,用于流体流动的研究。与分子动力学(MD)相比,DPD可以模拟更大尺度的长度和时间,而且避免了格子气体模型中与格子相关的人为效应。DPD中的粒子自由移动,不受固定格子约束,粒子的运动和相互作用完全依赖于它们之间的距离和相对速度,即不依赖于任何格子结构,因此是一种拉格朗日(随流体移动的)方法。因此它天然满足伽利略不变性(物理定律在不同惯性参考系下是相同的)和各向同性。
关于人为影响:在格子气体模型(如LBM)中,流体被离散化为分布在固定格子上的粒子。这些格子的几何形状(如正方形或六边形)可能会引入所谓的“人为效应”或“格子伪影”,这意味着模拟结果中可能会出现与格子形状相关的非物理特征。例如,正方形格子可能会偏好与格子轴对齐的流动方向,这不是真实流体的物理属性,而是模拟方法的一个副作用。
DPD的基本概念
-
粒子交互作用:DPD中的粒子代表分子团簇,具有质量。这些粒子通过三种不同的力进行相互作用:保守力(C)、耗散力(D)和随机力(R)。保守力是软性的,允许使用较大的时间步长进行模拟;耗散力模拟了流体中的粘性摩擦;随机力的作用就像是将粒子暴露在一个温度恒定的热浴中,热浴不断地向粒子注入或从粒子中抽取能量,模拟了真实物质中由于分子碰撞和相互作用产生的热效应。
-
动量守恒:DPD中所有的力都是粒子对之间的作用力(遵循牛顿第三定律),因此DPD保守动量。有时DPD被视为一种用于MD的动量守恒热浴(一个系统通过与外界交换能量来达到热平衡的过程)。
-
截断半径:所有粒子间的交互作用都有一个有限的作用范围,通常由截断半径 rc确定。超出这个距离,粒子间不再相互作用。
-
时间积分:DPD算法的一个关键方面是粒子位置和速度的时间积分,通常采用修正的速度-Verlet算法或跳蛙算法(数值积分算法)进行。
保守力(C):在DPD中,保守力是粒子间的一种排斥力,通常用来模拟粒子间的有效体积效应。这种力是“软”的,意味着粒子可以相互重叠,允许较大的时间步长进行模拟。
耗散力(D):耗散力是一种随粒子相对速度变化的摩擦力,用于模拟流体内部的粘性效应。
随机力(R):随机力是一种模拟热波动的力,为系统注入能量,帮助维持温度。这种力的引入使得DPD可以模拟热力学温度效应。
DPD的应用:
DPD特别适合于复杂流体(如悬浮的聚合物或生物细胞)在介观尺度上的流体动力学研究,也适用于复杂几何形状中的多相流动。多相流动指的是包含两种或两种以上不同相态(如液体、固体、气体)的流动。在多相流动中,不同相之间的界面动力学和相互作用对流动特性有重要影响。DPD因能够模拟复杂的界面现象和相互作用,特别适用于多相流动的研究。固体边界通常模拟为冻结的DPD粒子,而浸没的软结构(如聚合物)则通过用弹性弹簧连接的粒子来描述。
DPD的挑战
复杂的参数选择:DPD的一个缺点是它包含许多需要谨慎选择的参数,如粒子间作用力的径向权重函数。这些参数的选择对流体的宏观行为有显著影响。例如,为了达到较高的粘度,可能需要增加截断距离 rc,但这又会增加模拟的计算成本。
3.5 多粒子碰撞动力学
多粒子碰撞动力学(Multi-Particle Collision Dynamics, MPC)是一种模拟复杂流体系统的粒子方法,特别适用于同时需要考虑流体动力学相互作用和热涨落的系统。MPC通过粗粒化物理系统,即简化系统的微观细节,同时保留解决问题所必需的基本特征。尽管MPC在某种意义上是直接模拟蒙特卡罗(DSMC)方法的一个变体,但两者通常应用于完全不同的场景。特别是,MPC适用于平均自由程较小的系统,而DSMC适用于平均自由程较大的稀薄气体模拟。
热涨落是由于温度导致的系统微观状态随时间的随机变化。平均自由程指粒子在相继碰撞之间行进的平均距离,用于衡量气体分子的稀薄程度,平均自由程越长,意味着粒子之间的碰撞更少,气体越稀薄。
MPC方法的核心特点:
-
交替的流动和碰撞步骤:MPC算法交替执行流动(粒子移动一个时间步长)和碰撞(粒子在局部范围内随机碰撞并交换动量)步骤。
-
局部守恒定律:与标准的格子玻尔兹曼方法(LBM)不同,MPC不仅保证了质量和动量的局部守恒,而且还保证了能量的局部守恒。
-
各向同性离散化:MPC采用的离散化手段保证了方法的各向同性,这使得MPC可以作为一种可行的Navier-Stokes方程求解器使用。
MPC的应用:
MPC特别适用于模拟胶体、聚合物、脂质体和生物细胞等复杂系统,这些系统中流体动力学相互作用和热涨落都很重要。MPC的粒子基础特性使得它能够轻松地模拟溶剂和溶质的耦合系统。
MPC的挑战:
- Galilean不变性:最初提出的SRD算法违反了Galilean不变性,这个问题通过在每个碰撞步骤之前将格子随机移动一定距离来修正。
- 角动量守恒:SRD算法通常不保守角动量,这一问题可以通过特定的技术来避免。
总的来说,MPC提供了一种强大的工具来模拟涉及复杂流体动力学和热涨落的多组分系统。通过其粒子方法的特性,MPC能够以较低的计算成本捕捉到流体系统的宏观和介观行为
3.6 直接模拟蒙特卡罗方法
直接模拟蒙特卡罗(Direct Simulation Monte Carlo, DSMC)方法是一种基于动力学理论的粒子方法,由Bird在1960年代首创。DSMC通过模拟模型粒子之间的碰撞来获得流体流动的解决方案。这种方法特别适用于高克努森数(Knudsen number)流动的问题,克努森数是一个无量纲数,用于描述流体的平均自由程与特征长度之比,高克努森数通常意味着稀薄气体流动。DSMC的典型应用包括航天器技术和微系统。
DSMC方法的核心原理:
-
基于粒子的模拟:DSMC利用大量统计上具有代表性的粒子来追踪流体的行为。每个粒子的位置和速度在运动过程中是确定的,而粒子间的碰撞则通过概率模型来近似处理(即采用概概率模型来决定哪些粒子将会发生碰撞,因为微观尺度太过复杂,需要简化)。
-
概率碰撞模型:碰撞过程是DSMC中的关键步骤,通过选定的碰撞模型随机选择粒子进行碰撞模拟。这个概率过程区分了DSMC与其他如分子动力学(MD)等确定性模拟方法。
-
守恒律:碰撞模型遵循质量、动量和能量守恒定律,确保物理定律在模拟中得到严格遵守。
DSMC算法的四个主要步骤:
- 粒子流动:根据粒子的速度和时间步长更新粒子的位置。这一步骤需要考虑边界条件,如粒子与壁面的碰撞或粒子通过开放边界。
- 粒子索引和交叉引用:为了有效地处理粒子之间的碰撞,需要将计算域划分为若干小单元,并将粒子根据其位置归类到这些单元中。这样可以快速确定哪些粒子有可能发生碰撞。
-
模拟碰撞:在每个时间步内,基于概率模型随机选择粒子对进行碰撞模拟,碰撞规则确保质量、动量和能量守恒。
-
采样流场:在计算域的特定单元内,基于粒子的位置和速度计算宏观量,如密度、速度场等。这些宏观量是通过对所选单元内的粒子信息进行平均得到的。
DSMC的特点和应用:
- 显式和逐时间推进的技术:DSMC是一种随时间逐步求解的显式方法(即每个时间步的计算只依赖于上一个时间步的状态),通过采样和平均过程可以获得统计上准确的结果。
- 统计误差与计算成本:DSMC解的统计误差与粒子数的平方根成反比,而计算成本与粒子数成正比。因此,对于需要大量粒子的问题,DSMC的计算需求会非常高。
- 稀薄气体流动的优势:DSMC在稀薄气体流动领域特别有效,因为在这类问题中,DSMC的准确性/ 效率特性无与伦比。
- 计算资源的持续改进:随着计算资源的不断发展,预计DSMC在物理应用范围上将会得到扩展。
总之,DSMC提供了一种强大的工具来模拟稀薄气体流动,特别是在传统连续介质流体动力学方法不再适用的高克努森数条件下。通过直接模拟粒子的运动和碰撞,DSMC能够捕捉到复杂流动的微观行为,并以此预测流体的宏观特性。
3.7 平滑粒子流体动力学
平滑粒子流体动力学(Smoothed-Particle Hydrodynamics, SPH)是一种基于粒子的计算流体动力学方法,最初是在1970年代为解决三维天体物理学中的特定挑战而发明的。此后,SPH在许多领域得到了应用,包括近年来的计算机图形学,其中它能够相对低成本地模拟出令人信服的流体流动。SPH基于一个插值方案,使用影响其周围环境的点粒子(point particles)来表示流体。
SPH方法的核心是一种插值方案,该方案利用点粒子来模拟流体。点粒子的特征如下:
- 无体积:尽管点粒子被赋予质量,但在数学模型中它们没有体积,即被视为一个数学点。
- 位置和速度:每个点粒子在空间中有确定的位置和速度,这些属性随时间变化而更新,以模拟流体的运动。
- 物理量的载体:点粒子携带流体的物理量信息,如密度、温度等。这些信息可以通过点粒子间的相互作用和插值计算来获取流场中任何位置的宏观物理量。
在SPH方法中,流体被离散化为一系列点粒子,每个粒子代表流体的一小部分,并且携带该区域的宏观物理量信息。粒子之间的相互作用通过核函数来描述,该核函数定义了粒子的影响范围和强度。通过这种方式,SPH能够模拟复杂的流体动态,包括自由表面流动、多相流动和流体与固体的相互作用等。
SPH的优点:
- 自适应分辨率:SPH因其自适应分辨率而在处理大范围、密度变化巨大的无界域(如天体物理中的问题)时具有显著优势。(由于点粒子不依赖于固定的网格结构,SPH方法能够很好地处理复杂的几何形状和边界条件,以及流体域的大幅度变化。)
- 处理大变形问题:SPH能够处理极端问题,如爆炸和高速冲击等大变形问题,这些情况可能会使更传统的方法难以处理。
- 质量和动量守恒:SPH的粒子公式也完美守恒质量和动量。
SPH的缺点:
- 准确性问题:SPH在准确性方面存在问题,特别是在处理流体接近固体边界的情况时。
- 边界条件处理困难:处理SPH的边界条件不是非常简单,需要特殊的技巧和方法。
- 一致性证明困难:由于SPH的公式化方式,很难数学上证明数值方法与其意图模拟的流体动力学方程是一致的。
总之,SPH是一种强大的模拟工具,特别适合处理复杂流体动力学问题,其中流体可能经历大变形或流动域变化很大。尽管存在一些挑战,如准确性和边界条件的处理,但SPH在多个领域,包括天体物理学和计算机图形学中,都已经显示出其独特的价值。
四、Why Lattice Boltzmann?
格子玻尔兹曼方法(Lattice Boltzmann Method, LBM)是一种基于格子的计算流体动力学(CFD)方法,最初从格子气体模型发展而来。不同于直接追踪具体粒子的格子气体模型,LBM追踪的是粒子的分布函数。
4.1 LBM与其他方法的对比
-
物理基础:LBM有着强大的物理基础——玻尔兹曼方程。已有成熟的方法将LBM的动力学与流体的宏观守恒方程相联系。因此,标准LBM可被视为求解弱可压缩Navier-Stokes方程的二阶精度求解器。
-
实现简单:与传统方法(如FD、FV和FE)相比,LBM的实现更为简单,特别适合解决不可压缩的NS方程。
-
并行计算友好:LBM的计算主要局限于节点内,这使得其非常适合并行化处理,尤其是在现代高性能计算平台上,如GPU。
-
非线性与非局部性:传统方法在处理导数近似时往往涉及非局部计算,特别是在离散化非线性对流项时。而LBM中的复杂性主要在于节点内的粒子描述,使得非线性操作局限于节点内部,节点间的交互完全是线性的。这一特性使LBM非常适合于并行计算。
-
几何处理:LBM特别适用于处理复杂几何形状的质量守恒流动,如多孔介质流动模拟(指流体通过多孔固体材料(如岩石、土壤、海绵等)的流动)。
-
多相和多组分流动:LBM为多相和多组分流动(指同一相态中存在多种化学组分)提供了广泛的方法。结合其在复杂几何形状中的优势,LBM特别适合模拟复杂几何形状中的多相和多组分流动。
4.2 LBM的局限性
-
内存密集:LBM在流动过程中需要大量的内存访问,这可能成为计算的瓶颈。
-
稳态流动的效率:由于LBM固有的时依赖性,对于模拟稳态流动(流体的流动特性(如速度、压力等)在时间上不发生变化)来说并不特别高效。LBM算法本质上是一种时间演进的方法,它通过迭代地更新每个时间步的粒子分布函数来模拟流体流动的动态过程。
-
能量守恒:在LBM中进行能量守恒(热)模拟并不直接。
-
声音和可压缩性:LBM作为一个弱可压缩Navier-Stokes求解器,可能适合模拟声波和流动相互作用的情况,但对于直接模拟长距离的声波传播或强可压缩流动(如跨音速和超音速流动)则不太适合。
五、总结
本篇概述了两大类数值方法在流体动力学中的应用:传统方法和基于粒子的方法。
传统方法:
传统方法主要包括有限差分法(FD)、有限体积法(FV)和有限元法(FE)。这些方法将流体变量(如速度和压力)表示为定义在整个流域内各点(节点)上的数值。这些方法的共同点在于,它们利用节点上的数值来近似偏微分方程中的导数。
- 有限差分法(FD):在一个规则的方形网格上定义流场,直接在这些节点上求解流体变量,放弃了连续场的概念。
- 有限体积法(FV):每个节点上的值代表其周围小体积内流体变量的平均值,通过控制体积的边界上的通量来求解流体变量。
- 有限元法(FE):通过节点值的某种插值来近似连续场,通常用于复杂几何形状的流体流动问题。
尽管这些方法原理上相对简单(FE比FD和FV复杂一些),但流体动力学方程的固有难度(如非线性、同时求解多个方程、处理湍流或复杂几何形状的流动等)使得它们变得复杂。这导致了如SIMPLE和SIMPLER这样的复杂迭代算法的开发。
基于粒子的方法:
与传统方法直接求解流体动力学方程不同,基于粒子的方法通过模拟粒子(可能代表原子、分子、分子集合或宏观流体的一部分)来表示流体。这些方法多样且常针对特定问题量身定制。虽然最初格子气体模型用于流动模拟,但由于微观粒子群体中的波动导致的噪声问题,后来被格子玻尔兹曼方法(LBM)取代。LBM采取介观方法,消除了这种噪声。
总的来说,不同的求解器有其各自的优势和劣势,不同类型的流体模拟对求解器的要求也不同。因此,普遍认为没有一种方法能够在所有方面都优于其他方法。选择合适的模拟方法需要根据具体问题的需求和求解器的特点来决定。
相关文章:
(1))
论文阅读,The Lattice Boltzmann Method: Principles and Practice(六)(1)
目录 一、流体模拟方法概述 二、传统的Navier-Stokes求解器 2.1 有限差分 2.2 有限体积法 2.3 有限元法 三、基于粒子的求解器 3.1 动力学理论 3.2 分子动力学 3.3 格子气体模型 3.4 耗散粒子动力学 3.5 多粒子碰撞动力学 3.6 直接模拟蒙特卡罗方法 3.7 平滑粒子流…...
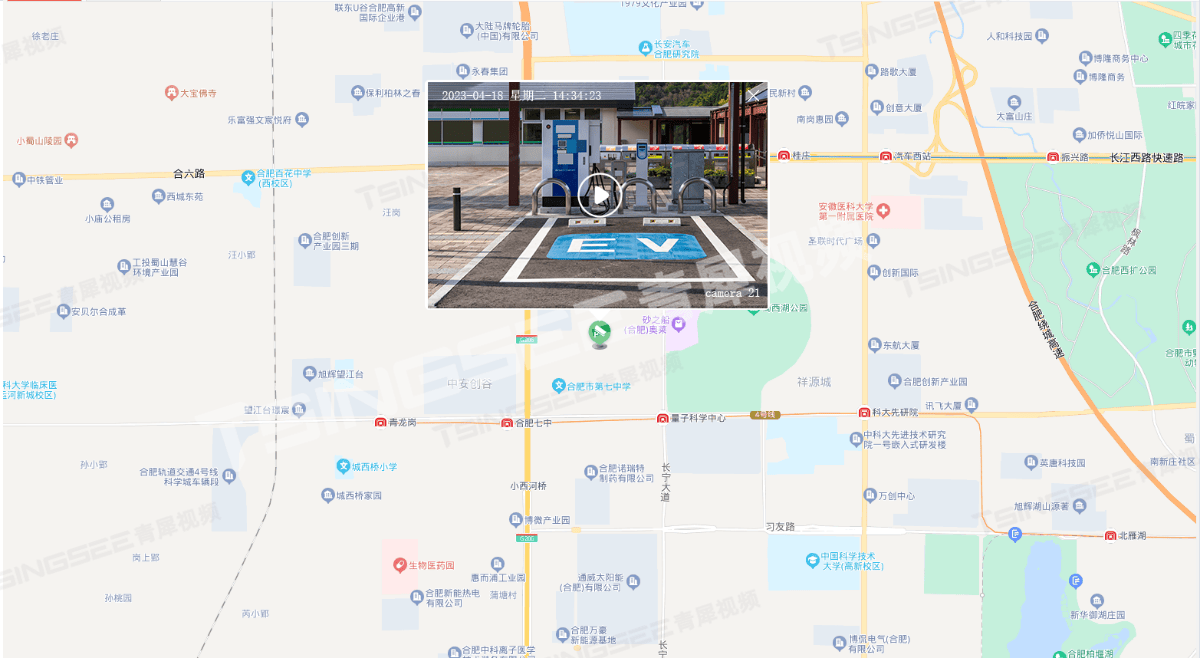
新能源充电桩站场视频汇聚系统建设方案及技术特点分析
随着新能源汽车的普及,充电桩作为新能源汽车的基础设施,其安全性和可靠性越来越受到人们的关注。为了更好地保障充电桩的安全运行与站场管理,TSINGSEE青犀&触角云推出了一套新能源汽车充电桩视频汇聚管理与视频监控方案。 方案采用高清摄…...
三、音频隐写[Audacity、deepsound、dtmf2num、MMSSTV、虚拟声卡、MP3Stego]
工具 1.Audacity 下载:https://www.audacityteam.org/download/windows/ 使用: 删除:先用左键长按拖着选中内容,然后选择软件最上方菜单栏的编辑,然后选择“删除”,最后点击文件的导出音频就能成功导出…...

二、Web3 学习(区块链)
区块链基础知识 一、基础知识1. 区块链可以做什么?2. 区块链的三个特点 二、区块链的类型概括1. PoW2. PoS3. 私有链和联盟链 三、智能合约1. 什么是智能合约2. 如何使用智能合约 四、困境1. 三难选择的基本要素2. 这真的是一个三难选择吗? 五、比特币1. 什么是比特…...

Linux内网提权
一、SUID提权 前提条件: (1)SUID仅对二进制有效(2)执行者对于该程序需要有x的可执行权限(3)本权限仅在程序的执行过程中有效 1、设置SUID权限:(root权限) …...

聚观早报 | 抖音独立商城App上线;阿里云联发科合作
聚观早报每日整理最值得关注的行业重点事件,帮助大家及时了解最新行业动态,每日读报,就读聚观365资讯简报。 整理丨Cutie 3月29日消息 抖音独立商城App上线 阿里云联发科合作 苹果WWDC24官宣 恒大汽车2023年营收财报 亚马逊投资Anthro…...

第十四届蓝桥杯省赛C++ B组所有题目以及题解(C++)【编程题均通过100%测试数据】
第一题《日期统计》【枚举】 【问题描述】 小蓝现在有一个长度为100的数组,数组中的每个元素的值都在0到9的范围之内。数组中的元素从左至右如下所示: 5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2 7 0 5 8 8 …...
【御控物联】 IOT异构数据JSON转化(场景案例一)
文章目录 前言技术资料 前言 随着物联网、大数据、智能制造技术的不断发展,越来越多的企业正在进行工厂的智能化转型升级。转型升级第一步往往是设备的智能化改造,助力设备数据快速上云,实现设备数据共享和场景互联。然而,在生产…...
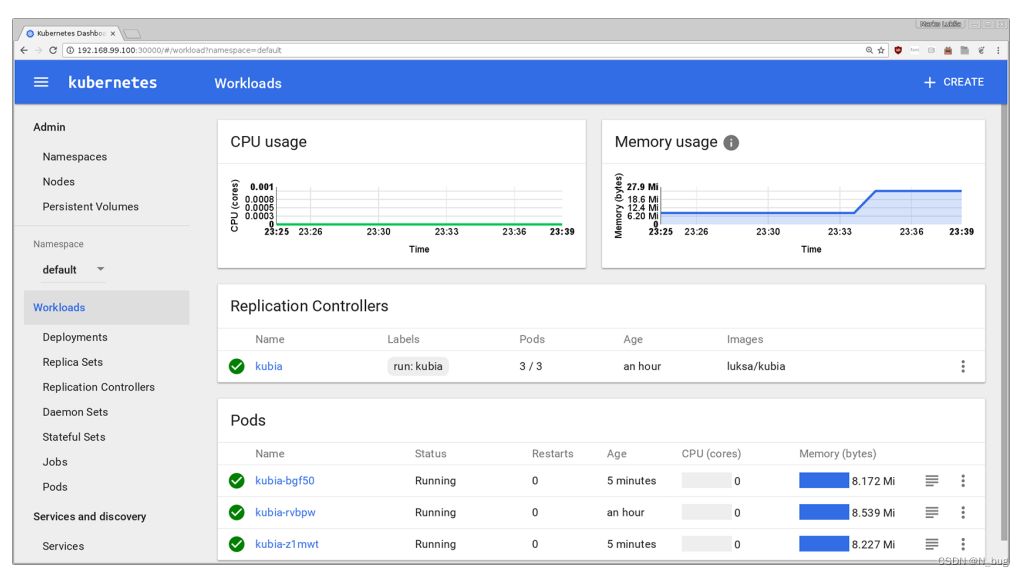
Kubernetes-running app on kube
Docker 安装Docker 首先,您需要在Linux机器上安装Docker。如果您不使用Linux,则需要启动一个Linux虚拟机(VM)并在该虚拟机中运行Docker。如果你使用的是Mac或Windows系统,并按照指令安装Docker, Docker将为你建立一个虚拟机,并在…...

简述如何系统地学习Python
随着人工智能、大数据和云计算等技术的快速发展,编程已经成为了当今社会中不可或缺的一项技能。Python作为一种高级编程语言,因其简洁明了的语法、强大的功能和广泛的应用领域,成为了许多初学者和专业人士的首选。那么,如何系统地…...

bsd猜想 Murmuration of Eliptic Curves(笔记)
BSD Alexey Pozdnyakov (University of Connecticut) YUTUBE视频, B站搬运地址新生代女数学家Nina Zubrilina得到椭圆曲线椋鸟群飞模式精确公式与证明 Arithmetic Geometry算术几何 希尔伯特第十问题 希尔伯特第十问题(Hilbert’s Tenth Problem&#…...

小米汽车正式发布:开启智能电动新篇章
随着科技的不断进步,汽车产业正经历着前所未有的变革。智能电动汽车作为这一变革的重要方向,正吸引着越来越多的目光。在这个充满机遇和挑战的时代,小米汽车凭借其卓越的技术实力和深厚的市场底蕴,终于迈出了坚实的一步。今天&…...

线性代数笔记25--复数矩阵、快速傅里叶变换
1. 复数矩阵 复向量 Z [ z 1 z 2 z 3 z 4 ⋯ ] Z\begin{bmatrix} z_1\\z_2\\z_3\\z_4\\ \cdots \end{bmatrix} Z z1z2z3z4⋯ 复向量的模长 ∣ z ∣ z ‾ ⊤ z [ z ‾ 1 z ‾ 2 z ‾ 3 ] [ z 1 z 2 z 3 ] \lvert z\rvert\overline z^{\top}z \begin{bmatrix…...

洛谷 P8783 [蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 1111, 最大 NM 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N,M 和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 …...

Rust 实战练习 - 8. 内存,ASM,外挂 【重磅】
目标: C写一个Demo版本的游戏由浅入深,了解外挂原理Linux/Android下实现内存读取ptrace实现内存修改(依赖第三方库) 先准备一个C写的小游戏 #include <stdio.h> #include <string.h>struct Role {float pos_x; // …...
XUbuntu22.04之Typora快捷键Ctrl+5不生效问题(二百二十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

GRE_MGRE综合实验
目录 1、R5为ISP,只能进行IP地址配置,其所有地址均配为公有IP地址。 IP配置 配置公网全网通 2、(1)R1和R5间使用PPP的PAP认证,R5为主认证方。 PAP认证 (2)R2与R5之间使用ppp的CHAP认证&am…...

把组合损失中的权重设置为可学习参数
目前的需求是:有一个模型,准备使用组合损失,其中有2个或者多个损失函数。准备对其进行加权并线性叠加。但想让这些权重进行自我学习,更新迭代成最优加权组合。 目录 1、构建组合损失类 2、调用组合损失类 3、为其构建优化器 …...

用Bat启动jar程序
前情提要:在使用冰蝎、哥斯拉等一些列工具时(PS:一系列需要利用Java环境并打开的jar),我就在想能不能写一段代码点一下,就能打开程序而不用去输入命令 echo off echo 程序启动中... start javaw -noverif…...

网站维护页404源码
网站维护页404源码,布局简洁,上传即可使用。 网站维护页404源码...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
