【No.21】蓝桥杯组合数学|数位排序|加法计数原理|乘法计数原理|排列数|组合数|抽屉原理|小蓝吃糖果|二项式定理|杨辉三角|归并排序(C++)
组合数学
数位排序
【问题描述】
小蓝对一个数的数位之和很感兴趣,今天他要按照数位之和给数排序。当两个数各个数位之和不同时,将数位和较小的排在前面,当数位之和相等时,将数值小的排在前面。
例如,2022 排在 409 前面, 因为 2022 的数位之和是 6,小于 409 的数位 之和 13。又如,6 排在 2022 前面,因为它们的数位之和相同,而6小于 2022
给定正整数 n,m,请问对1到n 采用这种方法排序时,排在第 m 个的元 素是多少?
【输入格式】
输入第一行包含一个正整数 n。
第二行包含一个正整数 m 。
【输出格式】
输出一行包含一个整数,表示答案。
题目详解
对于数字 1-n 而言,可以事先求出每个数字的数位之和。根据每个数字的数位之和自定义排序函数即可。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 10;
int a[maxn], b[maxn];//自定义排序函数
bool cmp(int x, int y)
{return b[x] < b[y] || b[x] == b[y] && x < y;
}int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i ++){//求i的数位之和int num = i;while (num)b[i] += num % 10;num /= 10;a[i] = i;}sort(a + 1, a + 1 + n, cmp);cout << a[m] << endl;return 0;
}
计数原理:加法原理
-
加法原理: 集合 S 被分成两两不相交的部分 S1,S2,S3,…,Sm,那么 S 的对象数目等于:∣S∣=∣S1∣+∣S2∣+∣S3∣+…+∣Sm∣
-
例: 一个学生想学一门数学课,一门文化课,但不能同时选,现在从 4 门数学课和 4 门文化课中选,一共有 4+4=8 种方法选一门课。
-
加法原理的关键是将计数分解为若干个独立(不相容)的部分,保证既不重复也不遗漏地进行计数。
-
加法原理是利用完备事件组的一个体现,我们可以利用一个集合的补集做题。
例题:分割立方体 lanqiaoOJ 题号 1620
题目描述:
一个立方体,边长为 n,分割成 n×n×n 个单位立方体。任意两个单位立方体,或者有 2 个公共点,或者有 4 个公共点,或者没有公共点。
请问,没有公共点和有 2 个公共点的立方体,共有多少对?
输入描述:
一个整数 n,1≤n≤30
思路:
反过来计算,先算出有 4 个公共点的立方体有多少对,然后用总对数减去。分几种情况讨论:
- 正方体和周围 3 个正方体相邻,这种情况共有 8 个,就是顶角上的 8 个,总个数 3×8;
- 正方体和周围 4 个正方体相邻,这种情况共有 (n−2)×12 个 (棱)总个数 4×(n−2)×12;
- 正方体和周围 5 个正方体相邻,这种情况共有 6×(n×n−4×n+4) 个,总个数 5×6×(n×n−4×n+4);
- 正方体和周围 6 个正方体相邻,这种情况共有 (n×n×n−n×n×6+n×12−8) 个,总个数 6×(n×n×n−n×n×6+n×12−8); 最后把这 44 个情况求和再除以 2。
正方体一共 n 3 n^3 n3 个,共有 n 3 ( n 3 − 1 ) 2 \frac{n^3(n^3-1)}{2} 2n3(n3−1) 种关系
- 正方体和周围 3 个正方体相邻,总个数 3×8;
- 正方体和周围 4 个正方体相邻,总个数 4×(n−2)×12;
- 正方体和周围 5 个正方体相邻,总个数 5×6×(n×n−4×n+4);
- 正方体和周围 66 个正方体相邻,总个数 6×(n×n×n−n×n×6+n×12−8);
- 最后把这 4 个情况求和再除以 2。
#include<bits/stdc++.h>
using namespace std;
int main()
{int n; cin >> n;if(n == 1){ // 边长为 1 时特判cout << 0 << endl;return 0;}long long sum = n * n * n * (n * n * n - 1) / 2; //总数int edge3 = 8;int ans3 = 3 * edge3;int edge4 = (n - 2) * 12;int ans4 = 4 * edge4;int edge5 = n * n - 4 * n + 4;int ans5 = 5 * 6 * edge5;int edge6 = n * n * n - n * n * 6 + n * 12 - 8;int ans6 = 6 * edge6;cout << sum - (ans3 + ans4 + ans5 + ans6) / 2 << endl;return 0;
}
计数原理:乘法原理
令 S 是对象的有序对 (a,b) 的集合,其中第一个对象 a 来自大小为 p 的一个集合,对于对象 a 的每个选择,对象 b 有 q 个选择,那么 S 的大小:∣S∣=p×q
例:中性笔的长度有 3 种,颜色有 4 种,直径有 5 种。不同种类的中性笔有:3×4×5=60 种。
例: 3 4 ∗ 5 5 ∗ 7 2 ∗ 1 1 3 3^4*5^5*7^2*11^3 34∗55∗72∗113 的正整数因子有多少?答:这是算数基本定理的概念。3 有 0 ~ 4 这 5 种选择,5 有 6 个选择,7 有 3 个选择,11 有 4 个选择,因子总数是 5×6×3×4=360 种。
排列数
排列是有序的。
不可重复排列数:从 n 个不同的物品中取出 r 个,排列数为:
A n r = n ( n − 1 ) ( n − 2 ) … ( n − r + 1 ) = n ! ( n − r ) ! A_{n}^{r}=n(n-1)(n-2)\dots (n-r+1)=\frac{n!}{(n-r)!} Anr=n(n−1)(n−2)…(n−r+1)=(n−r)!n!
可重复排列数,从 n 个不同的物品中可重复地取出 r 个的排列数为: n r n^r nr。
组合数
排列是有序的,组合是无序的。
如果 S 中的元素都不相同,组合数:
C n r = A n r r ! = n ! r ! ( n − r ) ! C_{n}^r=\frac{A_{n}^r}{r!}=\frac{n!}{r!(n-r)!} Cnr=r!Anr=r!(n−r)!n!
糊涂人寄信 lanqiaoOJ 题号 1622
题目描述:
有一个糊涂人,写了 n 封信和 n 个信封,到了邮寄的时候,把所有的信都装错了信封。求装错信封可能的种类数。
输入描述:
每行输入一个正整数 n,表示一种情况。(n≤20)
输出描述:
输出相应的答案。
解题思路:
题目建模为:有 1∼n 个数字,分别放在 n 个位置,问都放错的情况有多少种。
用 DP 来做。定义 dp[],dp[i] 表示数字 1∼i 都放错的种类数。dp[n] 是答案。
下面考虑状态转移方程,从 1∼i 递推到 i。
数字 i 如果放错,有 i−1 个位置可以放,(不能放在自己的位置上)假设其放在第 k 个位置。对于数字 k,可以放在 i 位置也可以不放在 i 位置。
- 如果 k 放在 i 位置,那么对于剩下 i−2 个数字放的次数,就是 i−2 个数字都放错的方法数
dp[i−2]。 - 如果 k 不放在 i 位置,和 i−1 个数字放错的情况相同,为
dp[i−1]。
状态转移方程:dp[i] = (i − 1)*(dp[i−1] + dp[i−2])
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[30];int main()
{dp[1] = dp[0]=0;dp[2] = 1;for(int i = 3; i <= 22; i ++) dp[i] = (i - 1) * (dp[i - 1] + dp[i - 2]);int n;while(cin >> n) cout << dp[n] << endl;return 0;
}
鸽巢原理
鸽巢原理,又称抽屉原理。
鸽巢原理: 把 n+1 个物体放进 n 个盒子,至少有一个盒子包含 2 个或更多的物体。
- 例:在 370 人中,至少有 2 人生日相同;
- 例:n 个人互相握手,一定有 2 个人握手次数相同。
n 个人互相握手,一定有 2 个人握手次数相同。 每人跟其他人握手,最少可以是 0 次,最多可以是n−1次。不存在重复握手
- 如果握手最少的是 0 次,那么剩下的n−1人中,握手最多的人不会超过n−2次。0∼n−2 共n−1种情况。
- 如果握手最少的张三是 1 次,那么剩下的n−1人中,握手最多的李四除了跟张三握手一次,跟其他n−2人最多握手n−2次,李四最多握手n−1次。1∼n−1 共n−1种情况。
- 如果握手最少的张三是 2 次,那么剩下的n−1人中,握手最多的李四除了跟张三握手一次,跟其他n−2人最多握手n−2次,李四最多握手n−1次。2∼n−1 共n−2种情况。
…… 所以握手次数最多有n−1种情况,最少只有 1 种情况。 把最多的n−1种情况看成n−1个抽屉,n个人放进这n−1个抽屉,至少有一个抽屉里面有 2 人。
例题:小蓝吃糖果 lanqiaoOJ 题号 1624
题目描述: Gardon 有 n 种糖果,每种数量已知。Gardon 不喜欢连续 2 次吃同样的糖果。问有没有可行的吃糖方案。
输入:
第一行是整数 N,0<n<1000000,
第二行是 n 个数,表示 n 种糖果的数量 m i m_{i} mi,0< m i m_{i} mi<1000000
输出:
输出一行,包含一个 “Yes” 或 “no”。
解题思路
继续处理格式,鸽巢原理,用“隔板法”求解。
找出最多的一种糖果,把它的数量 K 看成 K 个隔板,隔成 K 个空间(把每个隔板的右边看成一个空间);其它所有糖果的数量为 S。
- 如果 S<K−1,把 S 个糖果放到隔板之间,这 K 个隔板不够放,必然至少有 2 个隔板之间没有糖果,由于这 2 个隔板是同一种糖果,所以无解。
- S≥K−1 时,肯定有解。
其中一个解是:把 S 个糖果排成一个长队,其中同种类的糖果是挨在一起的,然后每次取 K 个糖果,按顺序一个一个地放进 K 个空间。由于隔板数量比每一种糖果的数量都多,所以不可能有 2 个同样的糖果被放进一个空间里。把 S 个糖果放完,就是一个解,一些隔板里面可能放好几种糖果。
#include <bits/stdc++.h>
using namespace std;
int a[1005000];int main()
{long long sum = 0;int Max = 0;int n; scanf("%d", &n);for (int i = 1; i <= n; i ++){scanf("%d", &a[i]);sum += a[i]; //所有糖果数量if(a[i] > Max) Max=a[i]; //最多的一种糖果}if(sum - Max + 1 >= Max) printf("Yes\n");else printf("No\n");return 0;
}
二项式定理和杨辉三角
杨辉三角:排列成如下三角形的数字
11 11 2 11 3 3 11 4 6 4 1
每个数是它上面 2 个数的和。
求杨辉三角第 n 行的数字,可以模拟这个推导过程,逐级递推,复杂度 O(n2)。
用数学公式计算,可以直接得到结果,这个公式是(1+x)n。
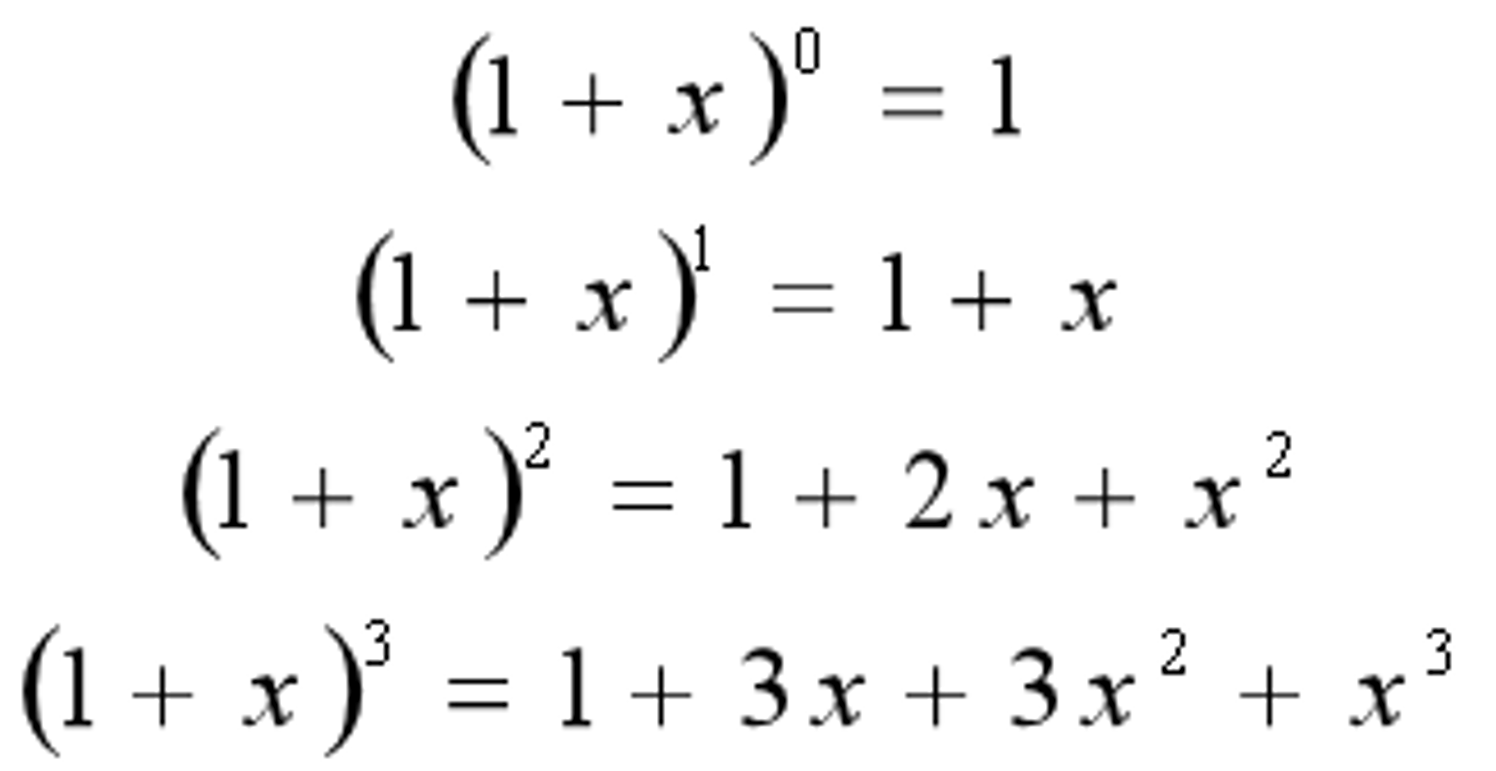
二项式系数就是 ( 1 + x ) n (1+x)^n (1+x)n 展开后第 r 项的系数。
C n r = n ! r ! ( n − r ) ! C_{n}^r=\frac{n!}{r!(n-r)!} Cnr=r!(n−r)!n!
对应杨辉三角的第 n 行第 r 个数是 C n − 1 r − 1 C_{n-1}^{r-1} Cn−1r−1
例:杨辉三角的第 4 行是“1331”,
C n − 1 r − 1 = C 4 − 1 1 − 1 = C 3 0 = 1 , C 3 1 = 3 , C 3 2 = 3 , C 3 3 = 4 C_{n-1}^{r-1}=C_{4-1}^{1-1}=C_{3}^0=1,C_{3}^1=3,C_{3}^2=3,C_{3}^3=4 Cn−1r−1=C4−11−1=C30=1,C31=3,C32=3,C33=4
理解: ( 1 + x ) n (1+x)^n (1+x)n的第 r 项,就是从 n 个 x 中选出 r 个,这就是组合数的定义
当 n 较大,且需要取模时,二项式系数有两种计算方法:
(1)递推公式:
C n r = C n − 1 r − + C n − 1 r − 1 C_{n}^{r}=C_{n-1}^{r-}+C_{n-1}^{r-1} Cnr=Cn−1r−+Cn−1r−1
公式是杨辉三角的定义,即“每个数是它上面 2 个数的和”。计算复杂度是 O ( n 2 ) O(n^2) O(n2)。
(2)用逆直接计算
因为输出取模,那么不用递推公式,直接用公式计算更快。不过,由于除法不能直接取模,需要用到逆。用逆计算二项式系数,有:
C n r = n ! r ! ( n − r ) ! C_{n}^{r}=\frac{n!}{r!(n-r)!} Cnr=r!(n−r)!n!
C n r C_{n}^r Cnr mod m = n ! r ! ( n − r ) ! \frac{n!}{r!(n-r)!} r!(n−r)!n! mod m = ( n ! n! n! mod m)( ( r ! ) − 1 (r!)^{-1} (r!)−1 mod m)( ( ( n − r ) ! ) − 1 ((n-r)!)^{-1} ((n−r)!)−1mod m)mod m
用逆计算二项式系数,复杂度是 O(n) 的。
杨辉三角形
【题目描述】
如果我们按从上到下、从左到右的顺序把杨辉三角形的所有数排成一列,可以得到如下数列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…给定一个正整数N,请你输出数列中第一次出现N是在第几个数?
【输入描述】
输入一个整数N。 N ≤ 1000000000 N \le 1000000000 N≤1000000000
【输出描述】
输出一个整数表示答案
题目解析
直接计算杨辉三角的每个数,然后推导出N的位置
下一行的2个数相加得下一行得一个数。例如上一行是b[0]~b[k],下一行是a[0]~a[k+1],那么a[i] = b[i-1] + b[i]
推算过程只用一个数组完成,和DP的自我滚动数组的原理一样,即a[i] = a[i-1] + a[i]
include <bits/stdc++.h>
using namespace std;
long long a[100050];
long long n, sum, line;//sum等于1~line行的数字个数
int main()
{cin >> n;sum = a[0] = 1;if(n == 1){ cout << l;return 0;}for (line = l; line < 50000; line ++)//line:杨辉三角的第1ine行{for (int i = line; i >= 1; i --)//倒过来循环,和DP的自我滚动数组的原理一样{a[i]= a[i-1] + a[i]; //上一行的2个数相加得下一行的一个数if(a[i] == n){cout << sum + line - i + 1;return 0;}}sum += (line+1);//1~line行的数字个数。每行比上一行多一个,累加}return 0;
}
代码只能通过40%的测试:
- 搜索范围小,只搜了前50000行;
- 运行时间是 O ( n 2 ) O(n^2) O(n2),即使只搜50000行,也超时了
- 如果是C++编码,会溢出。杨辉三角的有些数字可能很大,导致溢出。
本题的正解是用二分法加速
杨辉三角是左右对称的。所以若n在右边出现了,那也必然在左边出现过。而数列的构造顺序是从左往右,所以我们只需看左半部分即可。
上图并不是我们喜欢的杨辉三角形式,让我们再进行一步转换:
| 第0列 | 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
|---|---|---|---|---|---|---|
| 第0行 | 1 | |||||
| 第1行 | 1 | 1 | ||||
| 第2行 | 1 | 2 | 1 | |||
| 第3行 | 1 | 3 | 3 | 1 | ||
| 第4行 | 1 | 4 | 6 | 4 | 1 | |
| 第5行 | 1 | 5 | 10 | 10 | 5 | 1 |
| 第0列 | 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
|---|---|---|---|---|---|---|
| 第0行 | 1 | |||||
| 第1行 | 1 | |||||
| 第2行 | 1 | 2 | ||||
| 第3行 | 1 | 3 | ||||
| 第4行 | 1 | 4 | 6 | |||
| 第5行 | 1 | 5 | 10 |
我们知道杨辉三角的第i行第 j列的值为 C i j C_{i}^j Cij
用黄色印记标记的数字为我们需要考虑的部分(图一的左侧部分),我们称其为有效部分。
那么不难发现,对于每一列比如第i列),它们的有效部分都是从 C 2 i i C_{2i}^i C2ii开始的。即第i列的有效部分为 C 2 i i , C 2 i + 1 i , C 2 i + 2 i … C_{2i}^i,C_{2i+1}^i,C_{2i+2}^i\dots C2ii,C2i+1i,C2i+2i…
显然,对于同一行,列数越大则对应的数值也越大;对于同一列来说行数越大则数值也越大。也就是说如果某一行的某一列的值为 X,那么在列数不变的情况下,无论行数怎么变大都不会再出现比 X小的数了;同理在行数不变的情况下列数怎么变大也不会再出现比小的数了。
于是我们可得,当n≤ 1 0 9 10^9 109时,有效列数为第0~16列(因为第 17列的有效部分是从 C 17 C^{17} C17_34( C 17 C^{17} C17_34> 1 0 9 10^9 109)开始的,所以该列无论如何都不可能出现n了,其它的列就就更不可能了)。
我们考虑一列一列处理。那么对于某一列来说,我们怎么确定该列中是否存在n,若存在n这个n又会在该列的第几行呢?
由于随着行号的变大,数值是单调递增的,且知道了行号列号对应的数值也就知道了,于是就很显然可以二分行号。
设当前列数为i,那么二分的左边界l就为 2i,右边界r为 R(满足 C R i ≥ n C_{R}^{i}\ge n CRi≥n的任意 R都可)。然后不断搜索直到n出现后返回行号(或者直到搜索结束还是没找到n,返回 false),再计算出该行号、列号在数列中对应的位置即可
由于数列的构造顺序是从上到下、从左到右,所以我们需要从第16 列开始找,找到了即是答案直接退出程序,找不到再找第 15 列。。
复杂度为 O(16Clog)(C 为计算排列组合的复杂度)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n;
int C(int a, int b)
{int res = 1;for (int i = a, j = 1; j <= b; i ++){res = res * i / j;if (res > n)return res;}return res;
}
signed main()
{cin >> n;for (int k = 16; ~k; k --){int l = 2 * k;int r = max(n, l);int res = -1;while (l <= r){int mid = l + r >> 1;if (C(mid, k) >= n){res = mid;r = mid - 1;}elsel = mid + 1;}if (C(res, k) == n)cout << (res + 1) * res / 2 + k + 1 << '\n';}return 0;
}2*N 名编号为1~ 2N 的选手共进行 见 轮比赛。每轮比赛开始前,以及所有比赛结束后,都会按照总分从高到低对选手进行一次排名。选手的总分为第一轮开始前的初始分数加上已参加过的所有比赛的得分和。总分相同的,约定编号较小的选手排名靠前。
每轮比赛的对阵安排与该轮比赛开始前的排名有关:第1名和第2名、第3名和第4名、…第2K -1名和第 2K 名、…、第 2N -1名和策 2N 名,各进行一场比赛,每场比赛胜者得1分,负者得0分。也就是说除了首轮以外,其它轮比赛的安排均不能事先确定,而是要取决于选手在之前比赛中的表现。
现给定每个选手的初始分数及其实力值,试计算在R轮比赛过后,排名第Q的选手编号是多少。我们假设选手的实力值两两不同,且每场比赛中实力值较高的总能获胜。
暴力法:每轮做一次排序,R轮后输出
计算量:排序nlogn、共R轮=Rnlogn,超时
归并排序的思路:
每组比赛的胜者:赛前,总分按降序排;获胜后都得1分,仍是降序;
每组比赛的负者:赛前,总分按降序排的;不得分,仍是降序。
先按初始分数排序,然后按分数高低两人一组比赛
胜者入队A,负者入队B。这样A、B自身仍是有序的
那么:每次对于每轮比赛结束,只需进行合并操作即可,O(n)的时间就能让序列变成有序的了。
归并排序
![![[Pasted image 20240329121329.png]]](https://img-blog.csdnimg.cn/direct/9bc3ed241e5145bcb6b0a5ffac486e74.png)
归并排序的主要操作
- 分解。把初始序列分成长度相同的左右两个子序列,然后把每个子序列再分成更小的两个子序列…,直到子序列只包含1个数。用递归实现。
- 求解子问题,对子序列排序。最底层的子序列只包含1个数,其实不用排序。
- 合并。归并2个有序的子序列,这是归并排序的主要操作
对n个数进行归并排序:
- 需要logn趟归并;
- 在每一趟归并中,有很多次合并操作,一共需要O(n)次比较。
所以计算复杂度是O(nlogn)。
空间复杂度:需要一个临时的b[]存储结果,所以空间复杂度是O(n).
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, q, m,wn,ls;
struct Player
{int s, w, id;bool operator < (const player & x) const {if(x.sl = s)return s > x.s;return id < x.id;}
}P[N],winner[N], loser[N];
signed main()
{cin >> n >> m >> q;for (int i = 1; i <= n * 2; ++ i)P[i].id = i;for (int i = 1; i <= n * 2; ++ i)cin >> P[i].s;for (int i = 1; i <= n * 2; ++ i)cin >> P[i].w;sort(p+1, P + 1 + n * 2);while(m --){wn = ls = 0;for(int i = 1; i <= n; ++ i){if(P[i * 2].w > P[i * 2 - 1].w){P[i * 2].s ++;winner[++ wn] = P[i * 2];loser[++ ls] = P[i*2-1];}else {P[i * 2 - 1].s++;winner[++ wn] = p[i * 2 - 1];loser[++ ls] = P[i * 2];}}merge (loser + 1, loser + 1 + n, winner + 1, winner + 1 + n, P + 1);}cout << P[q].id << '\n';return 0;
}
相关文章:
【No.21】蓝桥杯组合数学|数位排序|加法计数原理|乘法计数原理|排列数|组合数|抽屉原理|小蓝吃糖果|二项式定理|杨辉三角|归并排序(C++)
组合数学 数位排序 【问题描述】 小蓝对一个数的数位之和很感兴趣,今天他要按照数位之和给数排序。当两个数各个数位之和不同时,将数位和较小的排在前面,当数位之和相等时,将数值小的排在前面。 例如,2022 排在 409 前面, 因为 2022 的数位之和是 6,小于 409 的数位 之和 13。…...

主流公链 - Monero
Monero: 加密货币的隐私标杆 1. 简介 Monero(XMR),世界语中货币的意思,是一种去中心化的加密货币,旨在提供隐私和匿名性。与比特币等公开区块链不同,Monero专注于隐私保护,使用户的交易记录和余…...

C#中让字典、列表、数组作为只读的方法参考
一、字典 在 C# 中,可以通过使用 ReadOnlyDictionary<TKey, TValue> 类或者是通过调用普通字典的 .AsReadOnly() 方法来创建一个只读的字典。ReadOnlyDictionary 不允许修改字典,任何试图改变字典的操作都会抛出 NotSupportedException。 以下是使…...

深入理解 React 中的 children props 和 render props
深入理解 React 中的 children props 和 render props 在 React 中,children props 和 render props 是两种常见的组件复用模式,它们都可以帮助我们更好地组织和复用组件代码。虽然它们的实现方式有所不同,但都能够有效地实现组件之间的数据…...

前端日期组件layui使用,月模式
初学前端,实战总结 概要 有一个日期组件,我的谷歌浏览器选完日期后,偶尔获取不到最新数据,有一个客户,是经常出不来数据。 日期组件是Wdate:调用的方法是WdatePicker onpicking,代码片段如下…...
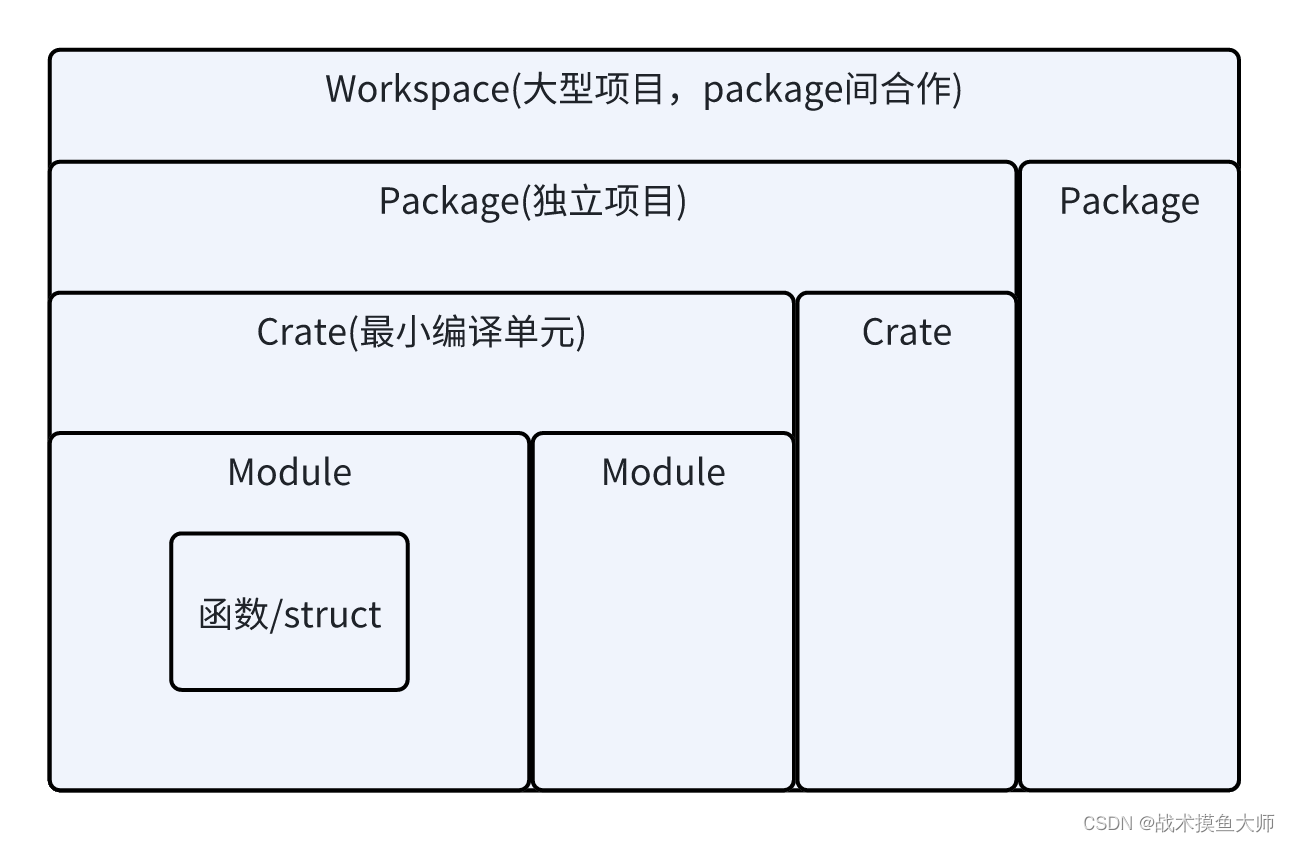
Rust编程(四)PackageCrateModule
这一部分的中文教程/文档都很混乱,翻译也五花八门,所以我建议直接看英文官方文档,对于一些名词不要进行翻译,翻译只会让事情更混乱,本篇从实战和实际需求出发,讲解几个名称的关系。 Module & Crate & Package & Workspace 英文中的意思: Cargo:货物 Crate:…...

命名空间【C++】(超详细)
文章目录 命名空间的概念命名空间的定义命名空间定义的位置作用域每一个命名空间都是一个独立的域作用域符:: 编译器找一个变量/函数等的定义,寻找域的顺序为什么要有命名空间?1.解决库与程序员定义的同名的重定义问题2.解决程序员…...

OceanBase OBCA 数据库认证专员考证视频
培训概述 OceanBase 认证是 OceanBase 官方推出的唯一人才能力认证体系,代表了阿里巴巴及蚂蚁集团官方对考生关于 OceanBase 技术能力的认可,旨在帮助考生更好地学习 OceanBase 数据库产品,早日融入 OceanBase 技术生态体系,通过由…...
卷积神经网络(CNN)——基础知识整理
文章目录 1、卷积神经网络 2、图片格式 3、图片卷积运算 4、Kernel 与 Feature Map 5、padding/边缘填充 6、Stride/步长 7、pooling/池化 8、shape 9、epoch、batch、Batch Size、step 10、神经网络 11、激活函数 1、卷积神经网络 既然叫卷积神经网络,这里面首先是…...
)
2024四川省赛“信息安全管理与评估“--网络事件响应--应急响应(高职组)
2024四川省赛“信息安全管理与评估“(高职组)任务书 2024四川省赛“信息安全管理与评估“任务书第一阶段竞赛项目试题第二阶段竞赛项目试题任务 1 应急响应(40分)第三阶段竞赛项目试题2024四川省赛“信息安全管理与评估“任务书 第一阶段竞赛项目试题 先略 第二阶段竞赛…...

Java类与对象:从概念到实践的全景解析!
个人主页:秋风起,再归来~ 文章专栏:javaSE的修炼之路 个人格言:悟已往之不谏,知来者犹可追 克心守己,律己则安! 1、类的定义格式 在java中定义类时需要用到…...

MySQL与SQLite区别
MySQL和SQLite都是关系型数据库管理系统(RDBMS),它们都使用SQL(结构化查询语言)作为标准查询语言。然而,尽管它们共享许多共同点,但它们在语法、功能、性能和存储机制方面存在一些差异。 以下是…...

【社会救助管理系统】主要设计及拟采用的技术方案
主要设计及拟采用的技术方案 1. 主要设计(1)系统架构设计(2)功能设计(3)安全性设计 2. 设计思想(1)系统架构设计思想(2)功能设计思想(3࿰…...

视频素材库哪个软件好?这8个高清无版权的素材网推荐
小伙伴们在制作短视频的时候,是不是为找素材发愁呢?一个高质量的无水印视频对创作者的帮助太大了,而且还需要无版权可商用的,那究竟有没有这样的网站呢?今天我来告诉大家。 1,蛙学府(中国&…...
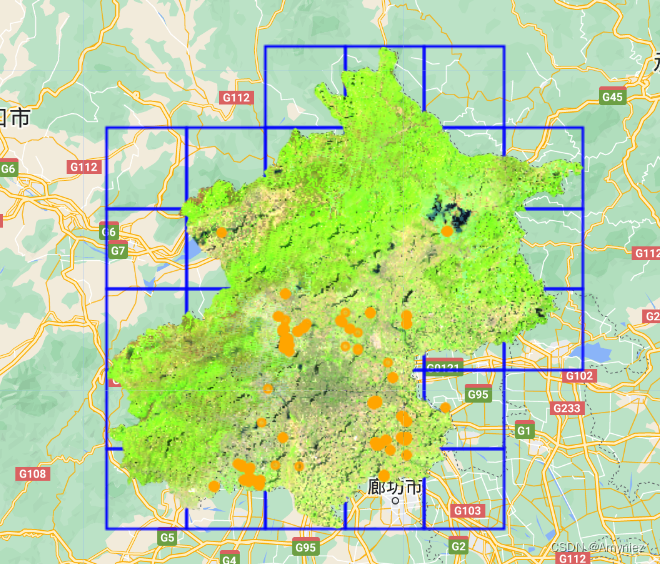
GEE23:基于植被物候实现农作物分类
地物分类 1. 写在前面2. 北京作物分类 1. 写在前面 今天分享一个有意思的文章,用于进行农作物分类。文章提出了一个灵活的物候辅助监督水稻(PSPR)制图框架。主要是通过提取植被物候,并自动对物候数据进行采样,获得足够多的样本点,…...

一些常见的Docker问题和答案
什么是Docker?它的主要功能是什么? Docker是一种开源的容器化平台,用于构建、部署和运行应用程序。它的主要功能包括:快速构建、分发和运行应用程序的容器化环境,实现应用程序的可移植性和可扩展性。 Docker和虚拟机…...
Web CSS笔记2
目录 1、背景 ①、背景图片(image) ②、背景平铺(repeat) ③、背景位置(position) ④、背景附着(attachment) ⑤、背景透明(CSS3) ⑥、背景图片缩放大小(size): ⑦、背景简写 2、标签显…...

SpringBoot -- 整合SpringMVC
SpringBoot已经替我们整合了许多框架并进行了默认的配置,我们只需要在依赖中导入spring-boot-starter-web,就可以直接使用SpringMVC以及web场景下的已经整合好的功能。但SpringBoot的默认配置可能无法满足我们所有的需求,那么我们怎么进行自定…...

C语言操作符详细讲解
前言 本次博客一定会让刚刚学习C语言小白有所收获 本次操作符讲解不仅分类还会有代码示例 好好看 好好学 花上几分钟就可以避免许多坑 1 操作符的基本使用 1.1操作符的分类 按功能分 算术操作符: 、- 、* 、/ 、% 移位操作符: >> << 位操作符…...

Godot 学习笔记(5):国际化多语言翻译,包含常用10种语言机翻!
文章目录 前言国际化翻译Api选择小牛测试 语言选择代码逻辑实体对象翻译帮助类导出模板读取文件翻译测试多语言测试 综合翻译文件准备测试代码测试结果 完整代码实体类翻译帮助类网络帮助类 最终效果翻译前翻译中翻译后 总结 前言 为了面向更大的市场,国际化是肯定…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
