LeetCode 2952.需要添加的硬币的最小数量:贪心(排序)
【LetMeFly】2952.需要添加的硬币的最小数量:贪心(排序)
力扣题目链接:https://leetcode.cn/problems/minimum-number-of-coins-to-be-added/
给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值,以及一个整数 target 。
如果存在某个 coins 的子序列总和为 x,那么整数 x 就是一个 可取得的金额 。
返回需要添加到数组中的 任意面值 硬币的 最小数量 ,使范围 [1, target] 内的每个整数都属于 可取得的金额 。
数组的 子序列 是通过删除原始数组的一些(可能不删除)元素而形成的新的 非空 数组,删除过程不会改变剩余元素的相对位置。
示例 1:
输入:coins = [1,4,10], target = 19 输出:2 解释:需要添加面值为 2 和 8 的硬币各一枚,得到硬币数组 [1,2,4,8,10] 。 可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 2 。
示例 2:
输入:coins = [1,4,10,5,7,19], target = 19 输出:1 解释:只需要添加一枚面值为 2 的硬币,得到硬币数组 [1,2,4,5,7,10,19] 。 可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 1 。
示例 3:
输入:coins = [1,1,1], target = 20 输出:3 解释: 需要添加面值为 4 、8 和 16 的硬币各一枚,得到硬币数组 [1,1,1,4,8,16] 。 可以证明从 1 到 20 的所有整数都可由数组中的硬币组合得到,且需要添加到数组中的硬币数目最小为 3 。
提示:
1 <= target <= 1051 <= coins.length <= 1051 <= coins[i] <= target
解题方法:排序 + 贪心
二话不说先对coins数组从小到大排个序。使用变量to记录当前能组成到几(初始值为0)。遍历coins数组:
- 如果
coins[i] <= to + 1,那么coins[i]就可以“拼接上”,原本可以组成的数据范围[1, 2, ..., to]加上coins[i]后就可以组成范围[1, 2, ..., to + coins[i]]。因此,更新to为to + coins[i]; - 否则(
coins[i] > to + 1)无法“拼接”,必须添加新的硬币。既然无法组成to + 1,那么必须要添加硬币to + 1。添加后便能组成到to + to + 1。
直到to >= target为止。
- 时间复杂度 O ( c o i n s log c o i n s + log t a r g e t ) O(coins\log coins + \log target) O(coinslogcoins+logtarget)(最多新增硬币
\log target次) - 空间复杂度 O ( log c o i n s ) O(\log coins) O(logcoins)
AC代码
C++
class Solution {
public:int minimumAddedCoins(vector<int>& coins, int target) {sort(coins.begin(), coins.end());int ans = 0, to = 0, i = 0;while (to < target) {if (i < coins.size() && coins[i] <= to + 1) {to += coins[i];i++;}else {to += to + 1;ans++;}}return ans;}
};
Python
# from typing import Listclass Solution:def minimumAddedCoins(self, coins: List[int], target: int) -> int:coins.sort()to, ans, i = 0, 0, 0while to < target:if i < len(coins) and coins[i] <= to + 1:to += coins[i]i += 1else:to += to + 1ans += 1return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/137185903
相关文章:
)
LeetCode 2952.需要添加的硬币的最小数量:贪心(排序)
【LetMeFly】2952.需要添加的硬币的最小数量:贪心(排序) 力扣题目链接:https://leetcode.cn/problems/minimum-number-of-coins-to-be-added/ 给你一个下标从 0 开始的整数数组 coins,表示可用的硬币的面值ÿ…...
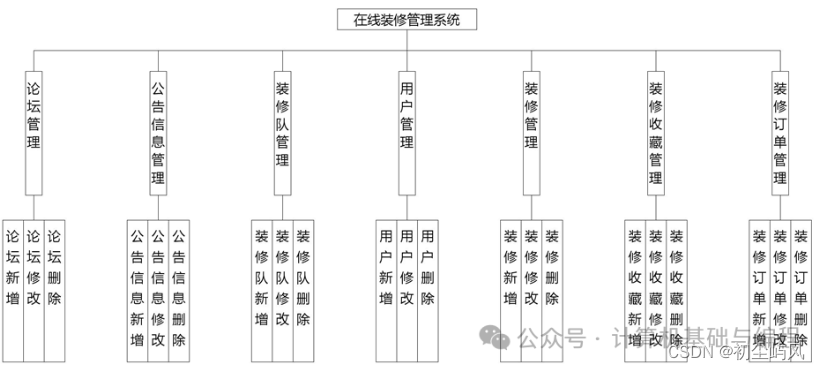
基于SpringBoot + Vue实现的在线装修管理系统设计与实现+毕业论文
介绍 系统包含用户、装修队、管理员三个角色 管理员: 管理员管理:管理其他管理员的账号和权限,确保系统管理的层次化和安全性。 装修队管理:审核装修队的资质,管理装修队的人员信息,监控工程进度ÿ…...
阿里云安全产品简介,Web应用防火墙与云防火墙产品各自作用介绍
在阿里云的安全类云产品中,Web应用防火墙与云防火墙是用户比较关注的安全类云产品,二则在作用上并不是完全一样的,Web应用防火墙是一款网站Web应用安全的防护产品,云防火墙是一款公共云环境下的SaaS化防火墙,本文为大家…...

作业 二维数组-定位问题
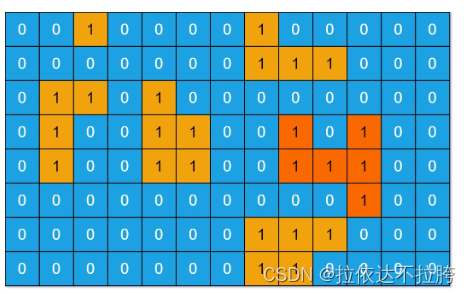
图形相似度 描述 给出两幅相同大小的黑白图像(用0-1矩阵)表示,求它们的相似度。 说明:若两幅图像在相同位置上的像素点颜色相同,则称它们在该位置具有相同的像素点。 两幅图像的相似度定义为相同像素点数占总像素点数…...
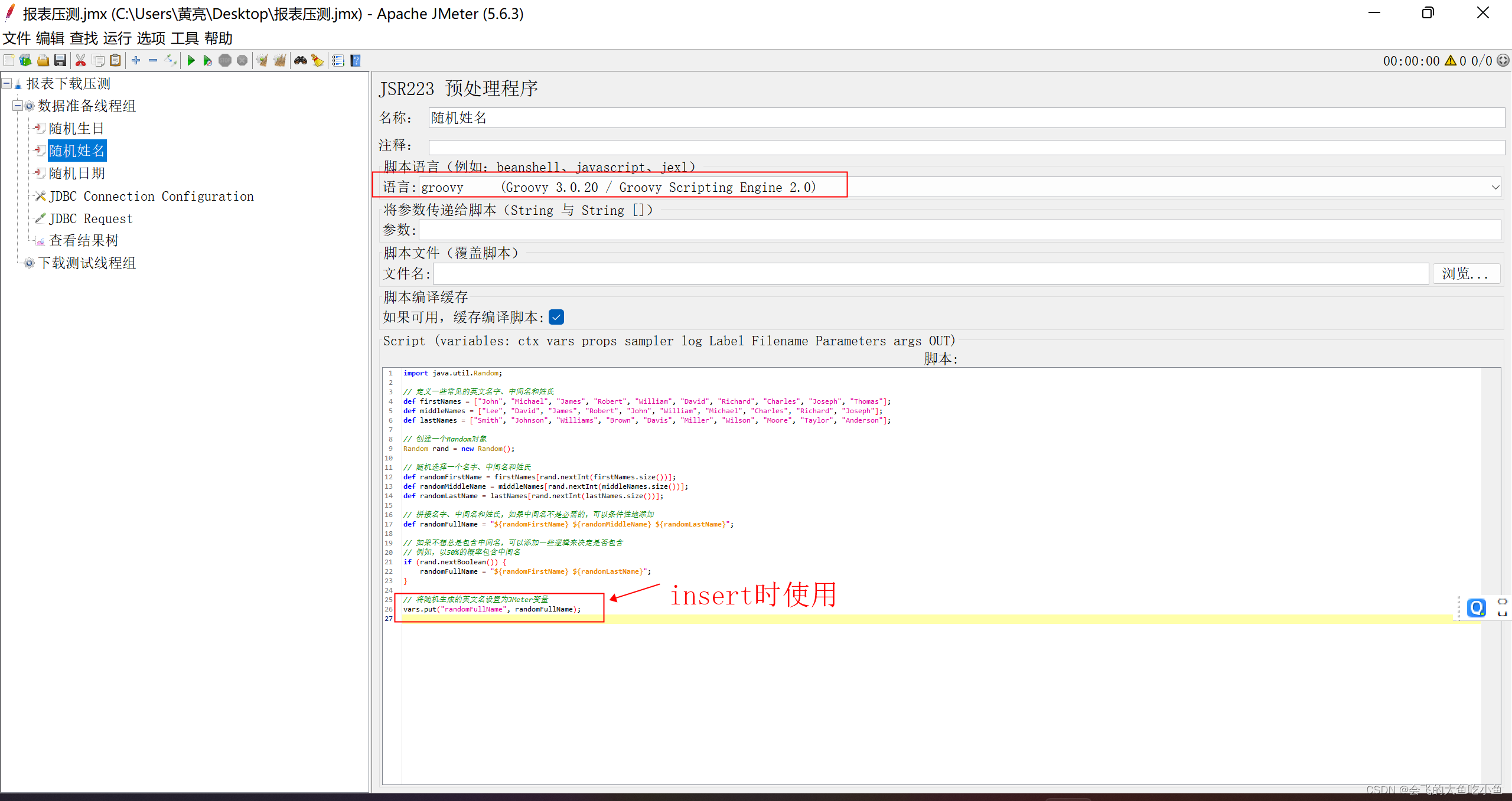
通过Jmeter准备压测数据-mysql示例
1、新建线程组 总共30万条数据 2、创建jdbc链接 创建jdbc连接配置 配置mysql连接 需要在jmeter安装的路径\apache-jmeter-5.6.3\lib\ext 目录下添加mysql 驱动 3、创建jdbc请求 jdbc链接名称需要与上一步中的保持一致,同时添加insert语句 例如 INSERT INTO test…...

如何系统的自学python?
系统地自学Python是一个循序渐进的过程,以下是一份详细的指南,帮助你从零开始逐步掌握这门语言: 1、了解Python及其应用场景: 阅读关于Python的简介,理解它为何流行,以及在哪些领域(如Web开发…...
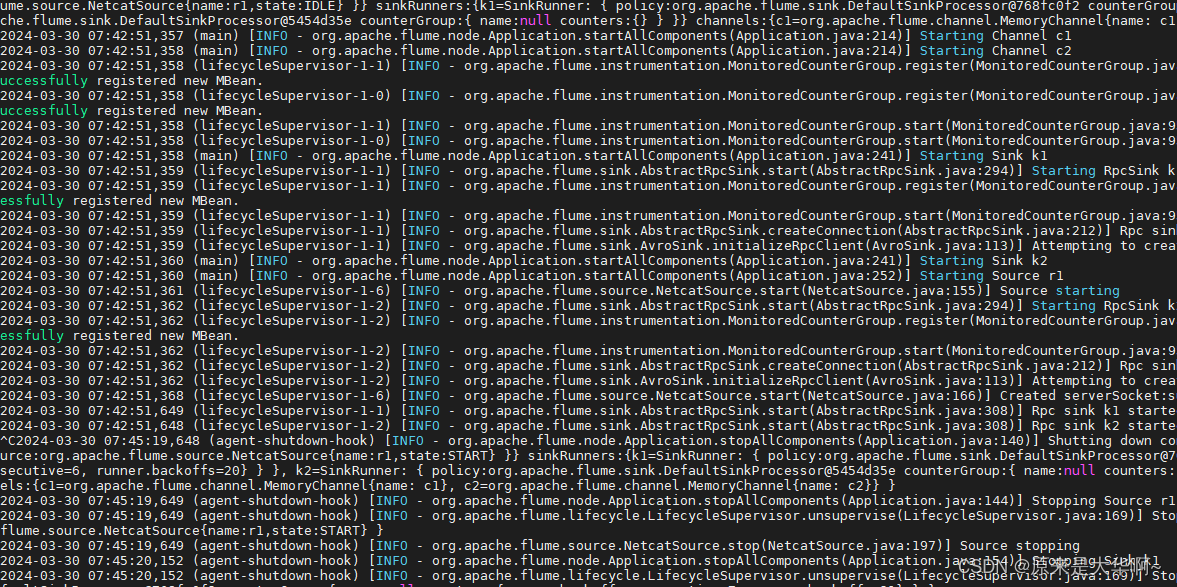
记录一个写自定义Flume拦截器遇到的错误
先说结论: 【结论1】配置文件中包名要写正确 vim flume1.conf ... a1.sources.r1.interceptors.i1.type com.atguigu.flume.interceptor.MyInterceptor2$MyBuilder ... 标红的是包名,表黄的是类名,标蓝的是自己加的内部类名。这三个都…...

Codeforces Round 934 (Div. 2) D. Non-Palindromic Substring
题目 思路: #include <bits/stdc.h> using namespace std; #define int long long #define pb push_back #define fi first #define se second #define lson p << 1 #define rson p << 1 | 1 const int maxn 1e6 5, inf 1e9, maxm 4e4 5; co…...

如何避免公网IP安全风险
目录 1. 使用防火墙 2. 定期更新和打补丁 3. 使用入侵检测和预防系统 4. 进行安全审计和监控 5. 实施最小权限原则 6. 使用VPN 7. 配置SSL/TLS 8. 使用DDoS保护服务 9. 强化认证措施 10. 定期备份数据 1. 使用防火墙 配置好网络防火墙,以允许仅必要的端口…...
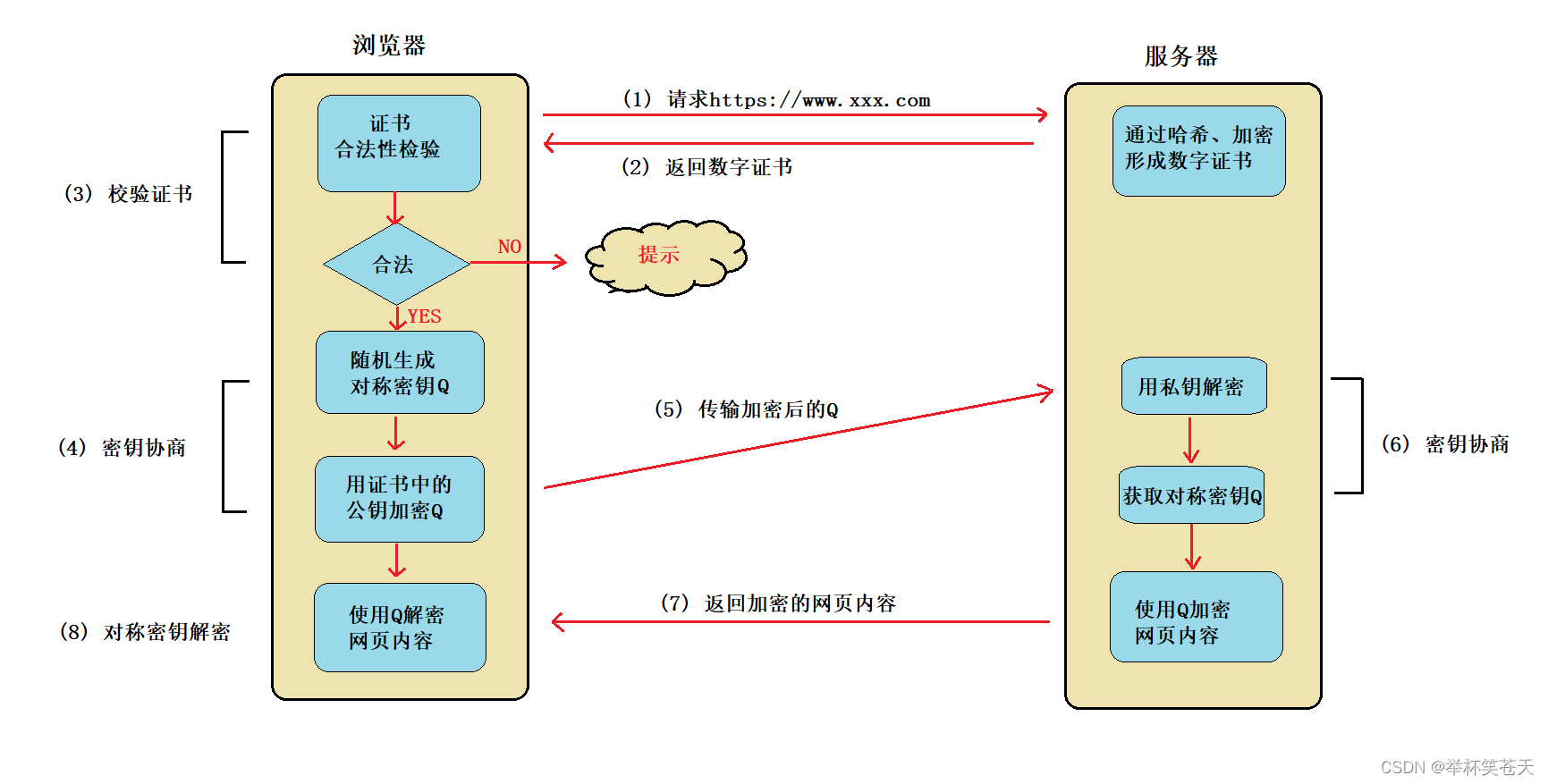
探究 HTTPS 的工作过程
目录 1. HTTPS 协议原理 1.1. 为什么要有HTTPS协议 1.2. 如何理解安全 1.3. HTTPS 协议是什么 2. HTTPS 的前置概念 2.1. 什么是加密 && 解密 2.2. 为什么要加密 2.3. 常见的加密方式 2.3.1. 对称加密 2.3.2. 非对称加密 2.4. 数据摘要 && 数据指纹…...
算法学习——LeetCode力扣图论篇1
算法学习——LeetCode力扣图论篇1 797. 所有可能的路径 797. 所有可能的路径 - 力扣(LeetCode) 描述 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特…...

Stable Diffusion 模型下载:epiCPhotoGasm(真实、照片)
本文收录于《AI绘画从入门到精通》专栏,专栏总目录:点这里,订阅后可阅读专栏内所有文章。 文章目录 模型介绍生成案例案例一案例二案例三案例四案例五案例六案例七案例八 下载地址 模型介绍 该模型对照片是什么有很高的了解,所以…...
WPF 路由事件 数据驱动 、Window 事件驱动
消息层层传递,遇到安装有事件侦听器的对象,通过事件处理器响应事件,并决定事件是否继续传递; 后置代码中使用AddHandler方法设置事件监听器,该方法的 第一个参数是指定监听的路由事件类型对象, 第二个参数…...

【UI框架】——保姆式使用教程
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
第10讲:操作符详解
第10讲:操作符详解 1. 操作符的分类2. 二进制和进制转换2.1 二进制转十进制10进制转2进制数 2.2 二进制转八进制和十六进制2.2.1 二进制转八进制2.2.2 二进制转十六…...
数据可视化Grafana Windows 安装使用教程(中文版)
1.跳转连接 天梦星服务平台 (tmxkj.top)https://tmxkj.top/#/site?url 2.下载应用程序 官网地址:Grafana get started | Cloud, Self-managed, Enterprisehttps://grafana.com/get/ 3.修改配置文件 grafana\conf\defaults 4.启动\bin\目录下serve应用程序 浏…...
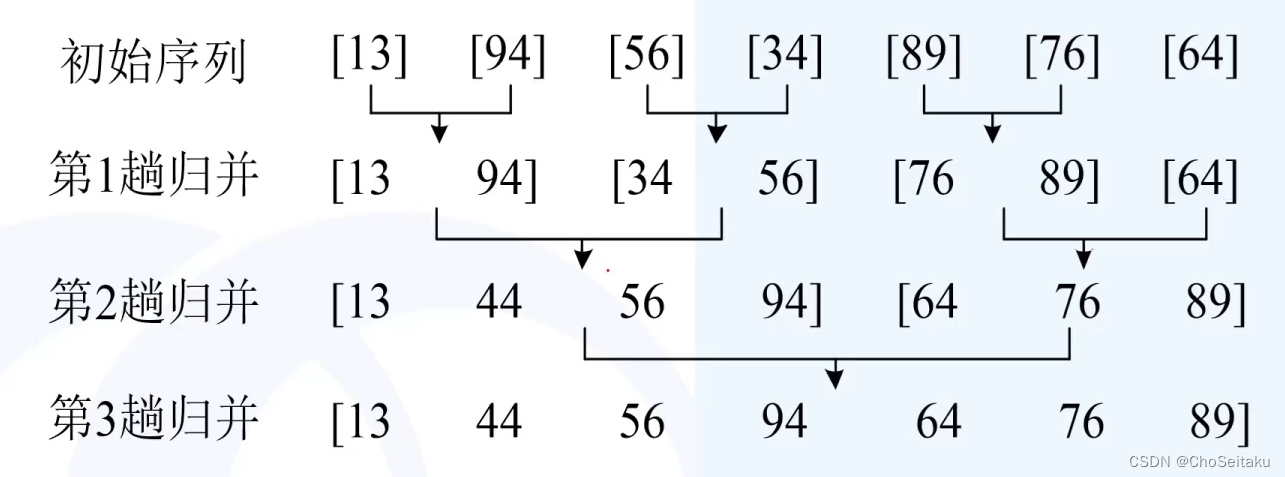
【No.21】蓝桥杯组合数学|数位排序|加法计数原理|乘法计数原理|排列数|组合数|抽屉原理|小蓝吃糖果|二项式定理|杨辉三角|归并排序(C++)
组合数学 数位排序 【问题描述】 小蓝对一个数的数位之和很感兴趣,今天他要按照数位之和给数排序。当两个数各个数位之和不同时,将数位和较小的排在前面,当数位之和相等时,将数值小的排在前面。 例如,2022 排在 409 前面, 因为 2022 的数位之和是 6,小于 409 的数位 之和 13。…...

主流公链 - Monero
Monero: 加密货币的隐私标杆 1. 简介 Monero(XMR),世界语中货币的意思,是一种去中心化的加密货币,旨在提供隐私和匿名性。与比特币等公开区块链不同,Monero专注于隐私保护,使用户的交易记录和余…...

C#中让字典、列表、数组作为只读的方法参考
一、字典 在 C# 中,可以通过使用 ReadOnlyDictionary<TKey, TValue> 类或者是通过调用普通字典的 .AsReadOnly() 方法来创建一个只读的字典。ReadOnlyDictionary 不允许修改字典,任何试图改变字典的操作都会抛出 NotSupportedException。 以下是使…...

深入理解 React 中的 children props 和 render props
深入理解 React 中的 children props 和 render props 在 React 中,children props 和 render props 是两种常见的组件复用模式,它们都可以帮助我们更好地组织和复用组件代码。虽然它们的实现方式有所不同,但都能够有效地实现组件之间的数据…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

高效的后台管理系统——可进行二次开发
随着互联网技术的迅猛发展,企业的数字化管理变得愈加重要。后台管理系统作为数据存储与业务管理的核心,成为了现代企业不可或缺的一部分。今天我们要介绍的是一款名为 若依后台管理框架 的系统,它不仅支持跨平台应用,还能提供丰富…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...
