蓝桥杯【奇怪的捐赠】c语言

我会将这题的解题的核心思路解为将10进制转化成7进制,毕竟题目上说的很清楚7的几次方
然后附上我认为的最优解
#include<stdio.h>
int main()
{int n = 1000000;int sum = 0;while (n != 0){int a;a = n % 7;n = n / 7;sum += a ;}printf("%d", sum);return 0;
}
//输出16
先看一下看的懂嘛?看不懂?没关系就算看不懂相信你对这个代码也有种陌生的熟悉感,和十进制转化为二进制很像
while (n != 0)
{a = n % 2;n = n / 2;sum += a * y;y *= 10;
}//10进制转化为2进制的代码
**但这题要求的是最多可以分给多少人,而不是7进制的代码,**所以只需要求n可以尽可能的被7的整数倍整除几次
举个例子假设n=10,那么这题的解就是4,
3+7=3 * 7^0+1 * 7^1
那n=100呢?那么题的解就为4,
2+98=2+49*2=2 * 7^0+2 * 7^2
还抽象吗?
第一个a求的是会有几个1,也就是几个7的0次方,
后面每一个非0的a求的都是当下7的最低的次方有几个。
带入100
100%7=2,所以有2个7的0次方
100-2=98,98/7=14,14/7=2,98里面有2个7的平方
很妙的一点就是a不等于0时都代表着几个a的几次方
相关文章:

蓝桥杯【奇怪的捐赠】c语言
我会将这题的解题的核心思路解为将10进制转化成7进制,毕竟题目上说的很清楚7的几次方 然后附上我认为的最优解 #include<stdio.h> int main() {int n 1000000;int sum 0;while (n ! 0){int a;a n % 7;n n / 7;sum a ;}printf("%d", sum);retu…...

【3月比赛合集】5场可报名的「创新应用」、「数据分析」和「程序设计」大奖赛,任君挑选!
CompHub[1] 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…)比赛。本账号会推送最新的比赛消息,欢迎关注! 以下信息仅供参考,以比赛官网为准 目录 创新应用赛(2场比赛)数据分析赛&#…...
vue3 视频播放功能整体复盘梳理
回顾工作中对视频的处理,让工作中处理的问题的经验固化成成果,不仅仅是完成任务,还能解答任务的知识点。 遇到的问题 1、如何隐藏下载按钮? video 标签中的controlslist属性是可以用来控制播放器上空间的显示,在原来默…...

vue-ueditor-wrap上传图片报错:后端配置项没有正常加载,上传插件不能正常使用
如图所示,今天接收一个项目其中富文本编辑器报错 此项目为vue2项目,富文本编辑器为直接下载好的资源存放在public目录下的 经过排查发现报错的函数在ueditor.all.min.js文件内,但是ueditor.all.min.js文件夹是经过压缩的 所以直接ÿ…...

数据仓库的发展历程
数据仓库的概念可以追溯到20世纪60年代,但真正形成理论并被企业广泛应用还需要一个较长的发展过程。大致可以分为以下几个阶段: 决策支持系统(DSS)时期(1960s-1970s) 这一时期,随着管理信息系统(MIS)和电子计算机的兴起,企业开始尝试构建面向决策的数据处理系统。最初的决策支…...
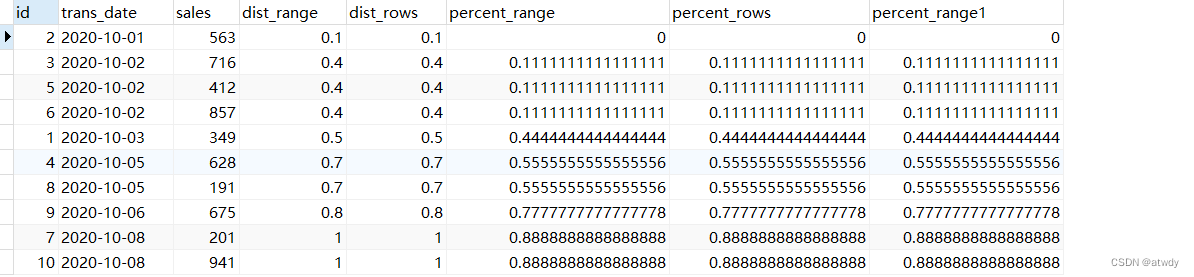
MySQL开窗函数
测试环境:mysql8.0.18 官方文档:https://dev.mysql.com/doc/refman/8.0/en/window-functions.html 一、窗口函数介绍二、语法结构三、自定义窗口1.rows(重点)2.range3.默认窗口 四、常用窗口函数示例1.row_number & rank &…...

Java学习笔记(23)
多线程 并发 并行 多线程实现方式 1.继承Thread类 自己创建一个类extends thread类 Start方法开启线程,自动执行重写之后的run方法 2.实现runable接口 自己创建一个类implements runnable Myrun不能直接使用getname方法,因为这个方法是thread类的方法…...
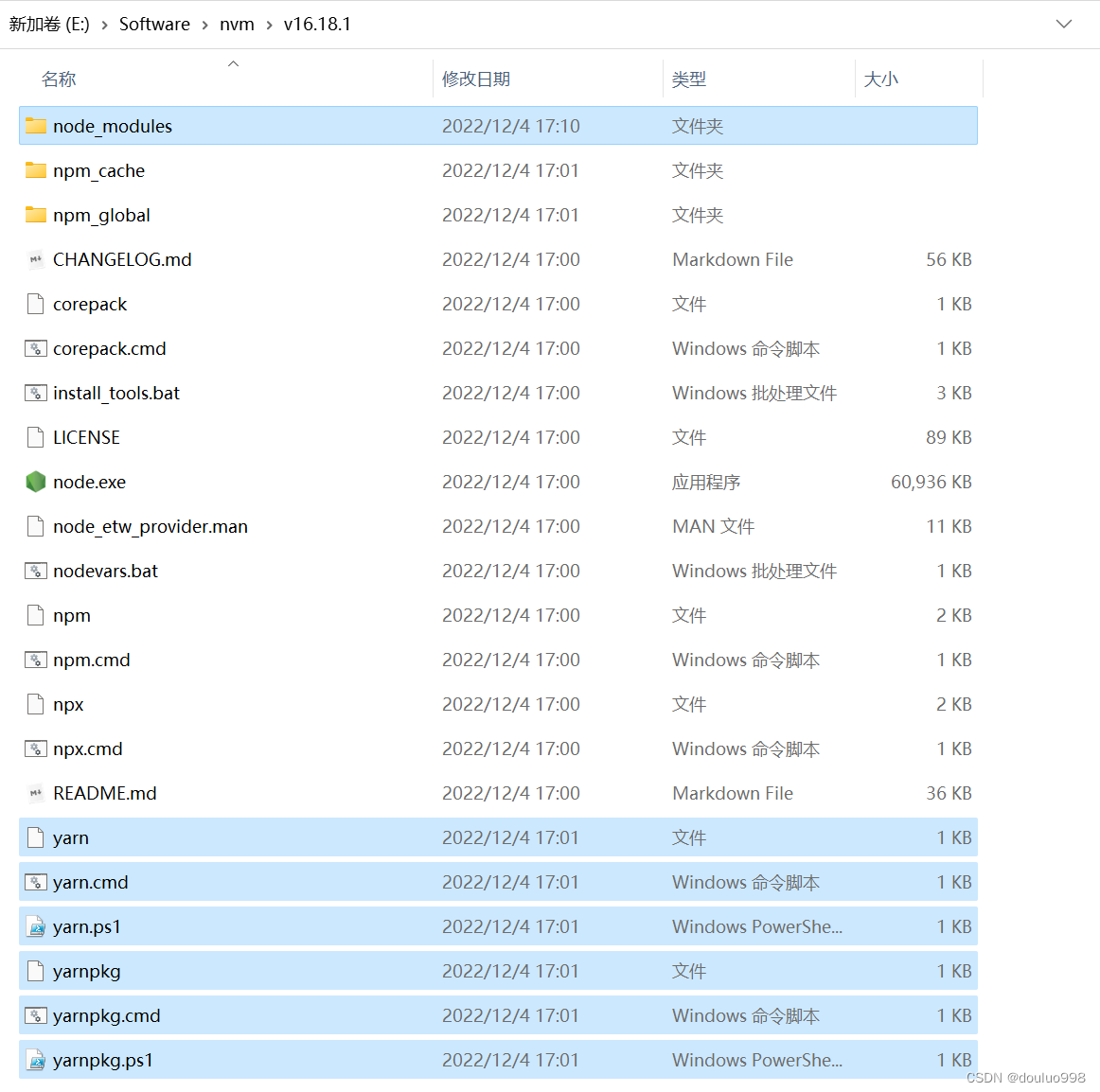
nodejs下载安装以及npm、yarn安装及配置教程
1、nodejs下载安装 1.1、使用nodejs版本管理工具下载安装,可一键安装、切换不同nodejs版本, nvm-setup.zip:安装版,推荐使用 本次演示的是安装版。 1、双击安装文件 nvm-setup.exe 选择nvm安装路径 例如:E:\Soft…...
方法执行JavaScript 表达式)
Playwright库page.evaluate()方法执行JavaScript 表达式
page.evaluate() 方法是 Playwright 中常用的方法之一,用于在页面上下文中执行 JavaScript 代码。它允许在浏览器环境中执行各种操作,如操作 DOM 元素、获取页面数据、执行复杂的计算等,并将结果返回到 Node.js 或 Python 代码中。 在 Playw…...
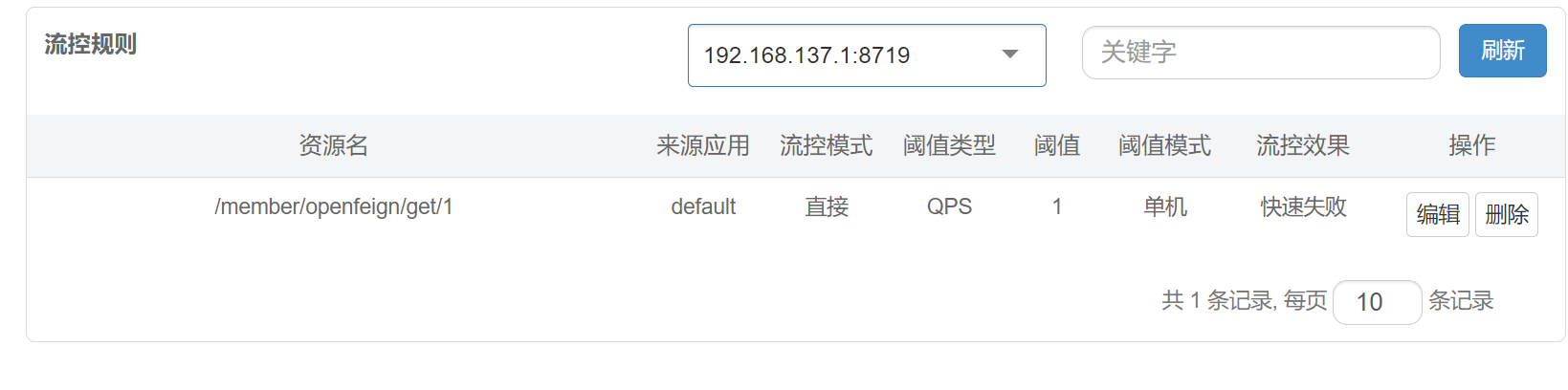
【微服务】OpenFeign+Sentinel集中处理远程调用异常
文章目录 1.微服务基本环境调整1.对10004模块的application.yml调整2.启动nacos以及一个消费者两个提供者3.测试1.输入http://localhost:8848/nacos/index.html 来查看注册情况2.浏览器访问 http://localhost:81/member/nacos/consumer/get/13.结果 2.使用OpenFeign实现微服务模…...

集合嵌套,Collections,斗地主案例,日志框架
文章目录 集合嵌套List嵌套ListList嵌套MapMap嵌套Map Collections类方法排序 sort 乱序 shuffle 斗地主案例需求思路代码 日志框架介绍优势体系结构Logback概述快速入门配置详解 集合嵌套 List嵌套List public static void main(String[] args){//一个年级有许多班级…...

maven pom relativePath属性的作用
maven pom relativePath属性的作用 文章目录 maven pom relativePath属性的作用一、relativePath出现的地方二、relativePath默认值三、四、<relativePath>一个pom路径 一、relativePath出现的地方 搭建maven项目,子模块指定父模块试,经常会在par…...

【STM32 HAL库SPI/QSPI协议学习,基于外部Flash读取。】
1、SPI协议 简介 SPI 协议是由摩托罗拉公司提出的通讯协议 (Serial Peripheral Interface),即串行外围设备接口,是 一种高速全双工的通信总线。它被广泛地使用在 ADC、LCD 等设备与 MCU 间,要求通讯速率 较高的场合。 SPI 物理层 SPI 通讯…...

Nginx入门--初识Nginx的架构
一、概述 Nginx的架构设计旨在高效处理并发的网络请求。它采用了事件驱动的、非阻塞的IO模型,可以同时处理成千上万个并发连接,而不会消耗太多的系统资源。 二、主要组件 Nginx的主要组件包括: Master Process(主进程…...

网络性能提升10%,ZStack Edge 云原生超融合基于第四代英特尔®至强®可扩展处理器解决方案发布
随着业务模式的逐渐转变、业务架构逐渐变得复杂,同时容器技术的兴起和逐渐成熟,使得Kubernetes、微服务等新潮技术逐步应用于业务应用系统上。 为了充分释放性能、为业务系统提供更高效的运行环境,ZStack Edge 云原生超融合采用了第四代英特尔…...

双非计算机考研目标211,选11408还是22408更稳?
求稳得话,11408比22408要稳! 很多同学只知道,11408和22408在考察的科目上有区别,比如: 11408考的是考研数学一和英语一,22408考察的是考研数学二和英语二: 考研数学一和考研数学二的区别大吗…...
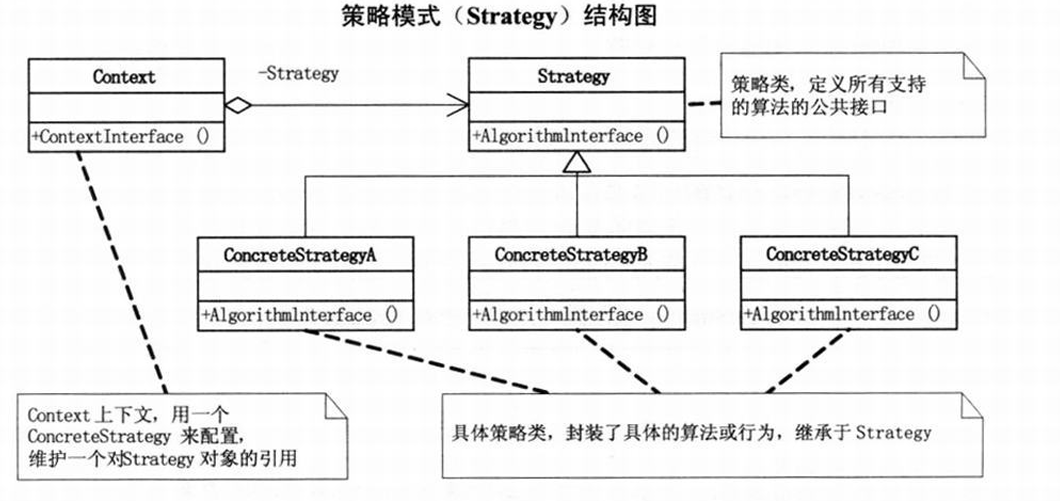
简单了解策略模式
什么是策略模式? 策略模式提供生成某一种产品的不同方式 Strategy策略类定义了某个各种算法的公共方法,不同的算法类通过继承Strategy策略类,实现自己的算法 Context的作用是减少客户端和Strategy策略类之间的耦合,客户端只需要…...

算法——运动模型
智能驾驶中常用的速度计算算法包括基于GPS的速度计算、惯性测量单元(IMU)的速度计算、雷达测距的速度计算、视觉测距的速度计算等。这些算法可以单独使用或者结合使用,以提高速度计算的准确性和稳定性。 智能驾驶中常用的加速度计算算法包括…...
基于R语言lavaan结构方程模型(SEM)技术应用
结构方程模型(Sructural Equation Modeling,SEM)是分析系统内变量间的相互关系的利器,可通过图形化方式清晰展示系统中多变量因果关系网,具有强大的数据分析功能和广泛的适用性,是近年来生态、进化、环境、…...

本地虚拟机服务器修改站点根目录并使用域名访问的简单示例
说明:本文提及效果是使用vmware虚拟机,镜像文件是Rocky8.6 一、配置文件路径 1. /etc/httpd/conf/httpd.conf #主配置文件 2. /etc/httpd/conf.d/*.conf #调用配置文件 调用配置文件的使用: vim /etc/httpd/conf.d/webpage.conf 因为在主配…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
