【蓝桥杯】矩阵快速幂
一.快速幂概述
1.引例
1)题目描述:
求A^B的最后三位数表示的整数,A^B表示:A的B次方。
2)思路:
一般的思路是:求出A的B次幂,再取结果的最后三位数。但是由于计算机能够表示的数字的范围是有限的,所以会产生“指数爆炸”的现象(即发生溢出现象)。
换一种思路来看本题:
取模运算的公式如下:
结论:
多个因子连续的乘积取模的结果等于每个因子取模后的乘积再取模的结果。
我们可以借助这个法则,只需要在循环乘积的每一步都提前进行“取模”运算,而不是等到最后直接对结果“取模”,也能达到同样的效果。
3)代码如下:
long long normalPower(long long a,long long b){long long result=1;for(int i=0;i<b;i++){result=(result*(a%1000))%1000;}return result%1000;
}
2.快速幂算法
1)思路:
快速幂算法能够帮我们算出指数非常大的幂。
传统算法时间复杂度高的原因是:指数很大,循环次数多。
核心思想:每一步都将指数分成两半,而相应的底数做平方运算。
2)代码:
//获取最后三位数
long long fastPower(long long base,long long power){long long re=1;while(power>0){if(power%2){//指数为奇数power--;//指数-1,将其变为偶数re=re*base%1000;}power/=2;base=base*base%1000;}return re;
}通过位运算进行优化:
long long FastPower(long long base,long long power){long long re=1;while(power>0){if(power&1){re=re*base%1000;}power=power>>1;base=(base*base)%1000;}return re;
}二.矩阵快速幂
矩阵乘法:
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++){for(k=1;k<=n;k++){c[i][j] += a[i][k] * b[k][j];}}
}矩阵快速幂:
仿照大数的快速幂
//矩阵快速幂
#include<iostream>
#include<cstring>
using namespace std;int M,n;struct node{int m[100][100];
}ans,res;//ans是结果,res为最初的方阵struct node mul(struct node A,struct node B){struct node C;int i,j,k;for(i=0;i<n;i++)for(j=0;j<n;j++)C.m[i][j]=0;for(i=0;i<n;i++){for(j=0;j<n;j++){for(k=0;k<n;k++){C.m[i][j]+=A.m[i][k]*B.m[k][j];}}}return C;
}void quickpower(){int i,j;//初始ans为单位矩阵for(i=0;i<n;i++)for(j=0;j<n;j++)if(i==j)ans.m[i][j]=1;elseans.m[i][j]=0;while(M>0){if(M&1){ans=mul(ans,res);}res=mul(res,res);M=M>>1;}
}
int main(){cin>>n;cin>>M;for(int i=0;i<n;i++)for(int j=0;j<n;j++)cin>>res.m[i][j];quickpower();for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<ans.m[i][j]<<' ';cout<<endl;}return 0;
}
三.实战演练
1.题目描述:

2.问题分析:
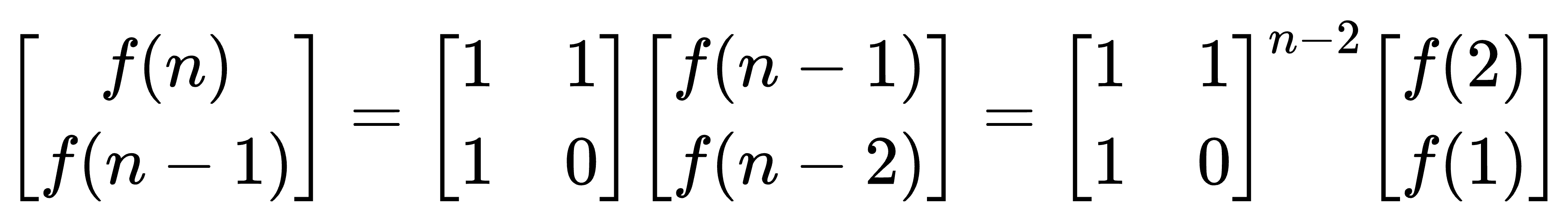
转换为矩阵相乘的形式。
3.代码实现:
//斐波那契数列
#include<iostream>using namespace std;const int N=1e4;
const long long mod=1e9+7;
int T;
long long a[N];struct node{long long m[2][2];
}ans,res;//矩阵乘法
struct node mul(struct node a,struct node b){struct node c;c.m[0][0]=(a.m[0][0]*b.m[0][0]+a.m[0][1]*b.m[1][0])%mod;c.m[0][1]=(a.m[0][0]*b.m[0][1]+a.m[0][1]*b.m[1][1])%mod;c.m[1][0]=(a.m[1][0]*b.m[0][0]+a.m[1][1]*b.m[1][0])%mod;c.m[1][1]=(a.m[1][0]*b.m[0][1]+a.m[1][1]*b.m[1][1])%mod;return c;
}//矩阵快速幂
struct node matrixPower(struct node base,long long exp){struct node res={1,0,0,1};while(exp>0){if(exp&1){res=mul(res, base);}exp=exp>>1;base=mul(base, base);}return res;
}//求斐波那契数列第n项
long long f(long long n){struct node base={1,1,1,0};struct node res=matrixPower(base, n-1);return res.m[0][0];
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>T;for(int i=0;i<T;i++){cin>>a[i];}for(int i=0;i<T;i++){cout<<f(a[i])<<'\n';}return 0;
}
相关文章:
【蓝桥杯】矩阵快速幂
一.快速幂概述 1.引例 1)题目描述: 求A^B的最后三位数表示的整数,A^B表示:A的B次方。 2)思路: 一般的思路是:求出A的B次幂,再取结果的最后三位数。但是由于计算机能够表示的数字…...

C语言使用STM32开发板手搓高端家居洗衣机
目录 概要 成品效果 背景概述 1.开发环境 2.主要传感器。 技术细节 1. 用户如何知道选择了何种功能 2.启动后如何进行洗衣 3.如何将洗衣机状态上传至服务器并通过APP查看 4.洗衣过程、可燃气检测、OLED屏显示、服务器通信如何并发进行 小结 概要 本文章主要是讲解如…...
【Hello,PyQt】QTextEdit和QSplider
PyQt5 是一个强大的Python库,用于创建图形用户界面(GUI)。其中,QTextEdit 控件作为一个灵活多用的组件,常用于显示和编辑多行文本内容,支持丰富的格式设置和文本操作功能。另外,QSlider 控件是一…...

【力扣】191.位 1 的个数、485.最大连续 1 的个数
191.位 1 的个数 题目描述 编写一个函数,输入是一个无符号整数(以二进制串的形式),返回其二进制表达式中 设置位 的个数(也被称为汉明重量)。 示例 1: 输入:n 11 输出࿱…...

蓝桥杯 java 承压计算
题目: 思路: 1:其中的数字代表金属块的重量(计量单位较大) 说明每个数字后面不一定有多少个0 2:假设每块原料的重量都十分精确地平均落在下方的两个金属块上,最后,所有的金属块的重量都严格精确地平分落在最底层的电子…...

leetcode268-Missing Number
这道题目要求缺失的数字,一般解决数组的问题,要么往排序数组,要么往双指针遍历这些方向上靠,要么往异或方向上靠,总之落点无非就只有这几个。我们要求缺失的数字,可以依次让1~n和数组元素进行异…...
【jenkins+cmake+svn管理c++项目】jenkins回传文件到svn(windows)
书接上文:创建一个项目 在经过cmakemsbuild顺利生成动态库之后,考虑到我一个项目可能会生成多个动态库,它们分散在build内的不同文件夹,我希望能将它们收拢到一个文件夹下,并将其回传到svn。 一、动态库移位—cmake实…...
数据结构·二叉树(2)
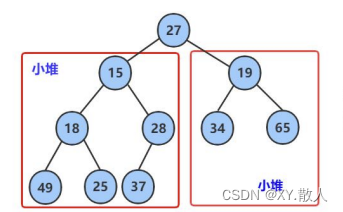
目录 1 堆的概念 2 堆的实现 2.1 堆的初始化和销毁 2.2 获取堆顶数据和堆的判空 2.3 堆的向上调整算法 2.4 堆的向下调整算法 2.4 堆的插入 2.5 删除堆顶数据 2.6 建堆 3 建堆的时间复杂度 3.1 向上建堆的时间复杂度 3.2向下建堆的时间复杂度 4 堆的排序 前言&…...

MATLAB算法实战应用案例精讲-【毕业季论文专用】人工智能视觉检测技术及其在实际应用中的挑战与前景
目录 摘要: 第一章:引言 1.1 研究背景 1.2 研究目的与意义...
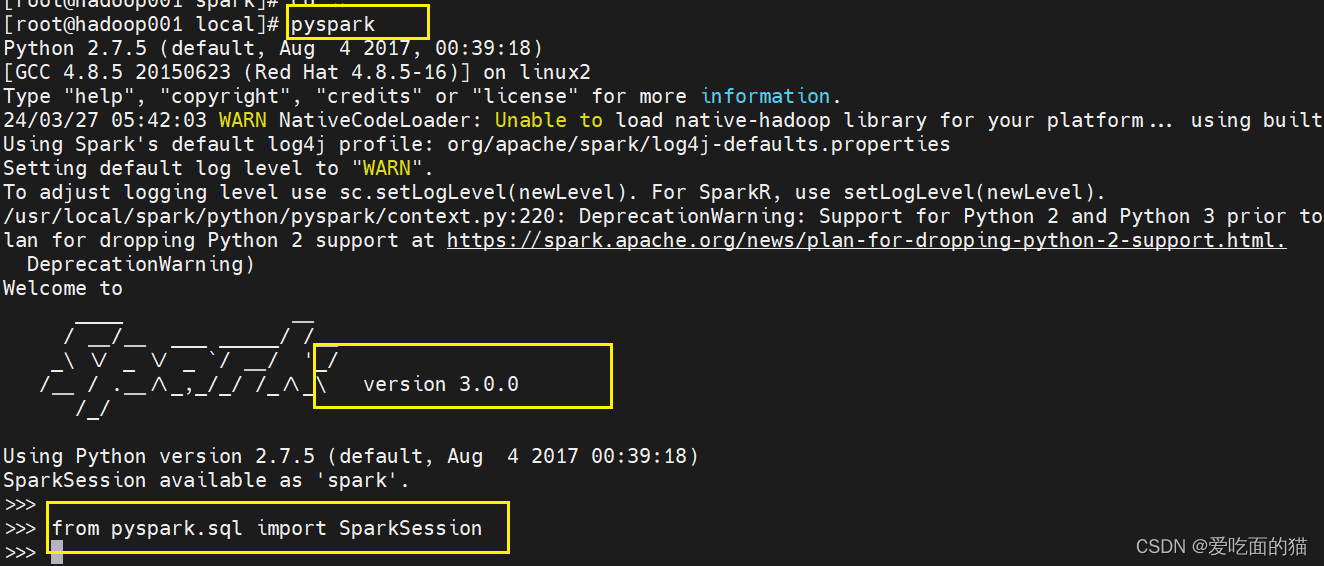
Linux虚拟机环境搭建spark
Linux环境搭建Spark分为两个版本,分别是Scala版本和Python版本。 一、 安装Pyspark 本环境以 Python 环境为例。 1、下载spark 下载网址:https://archive.apache.org/dist/spark 下载安装包:根据自己环境选择合适版本,本环境…...

STL的string容器
string基本概念 string是C风格的字符串,本质上是一个类。 string 和 char* 的区别 char* 是一个指针; string是一个类,内部封装了 char* ,用来管理字符串,是一个 char* 型的容器。 特点 string内部封装了很多成员…...

半导体工艺技术
完整内容点击:【半导体工艺技术】...

acwing算法提高之图论--单源最短路的扩展应用
目录 1 介绍2 训练 1 介绍 本专题用来记录使用。。。。 2 训练 题目1:1137选择最佳线路 C代码如下, #include <iostream> #include <cstring> #include <algorithm> #include <queue>using namespace std;const int N 101…...

SQLServer数据库使用Function实现根据字段内容的拼音首字母进行数据查询
实现SQL首字母查询分两步,第一步建Function,第二步引用新建的Function。 1. 首先需要自定义一个查询的Function,详细SQL如下: ALTER function [dbo].[GetDataByPY](str nvarchar(4000)) returns nvarchar(4000) as begin decla…...
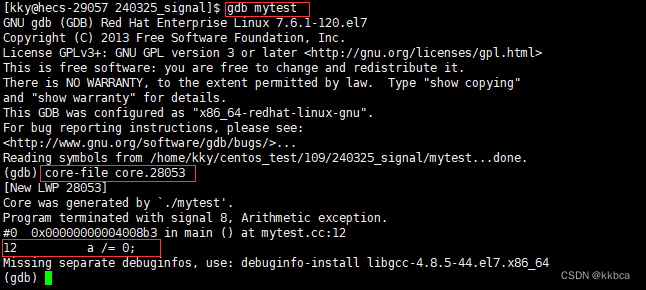
Linux——信号概念与信号产生方式
目录 一、概念 二、前台进程与后台进程 1.ctrlc 2.ctrlz 三、信号的产生方式 1.键盘输入产生信号 2.系统调用发送信号 2.1 kill()函数 2.2 raise()函数 2.3 abort()函数 3.异常导致信号产生 3.1 除0异常 3.2 段错误异常 4.软件条件产生信号 4.1 管道 4.2 闹钟…...
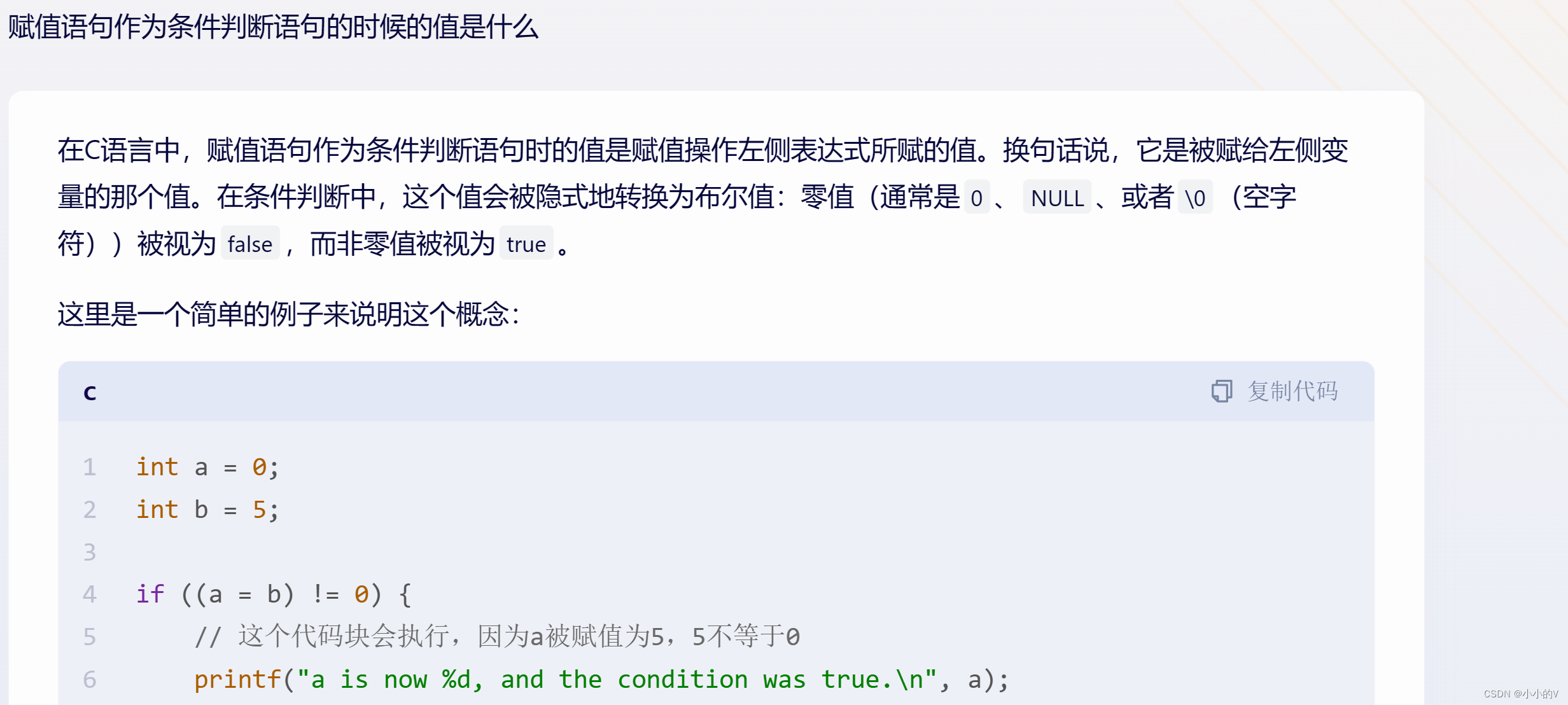
赋值语句还能当判断条件?涨芝士了!
赋值和条件看似是C语言中毫不相关的两个概念,虽然实际过程中我猜测不会有太多这种不太符合常理的情况出现,但是现在在学习的过程中,为了出题而出题总是会整出一些花活出来.....这很难不让人联想起高中时一些大佬为了彰显自己的数学天赋而自己…...
数据结构 - 算法效率|时间复杂度|空间复杂度
目录 1.算法效率 2.时间复杂度 2.1定义 2.2大O渐近表示法 2.3常见时间复杂度计算举例 3.空间复杂度 3.1定义 3.2常见空间复杂度计算举例 1.算法效率 算法的效率常用算法复杂度来衡量,算法复杂度描述了算法在输入数据规模变化时,其运行时间和空间…...
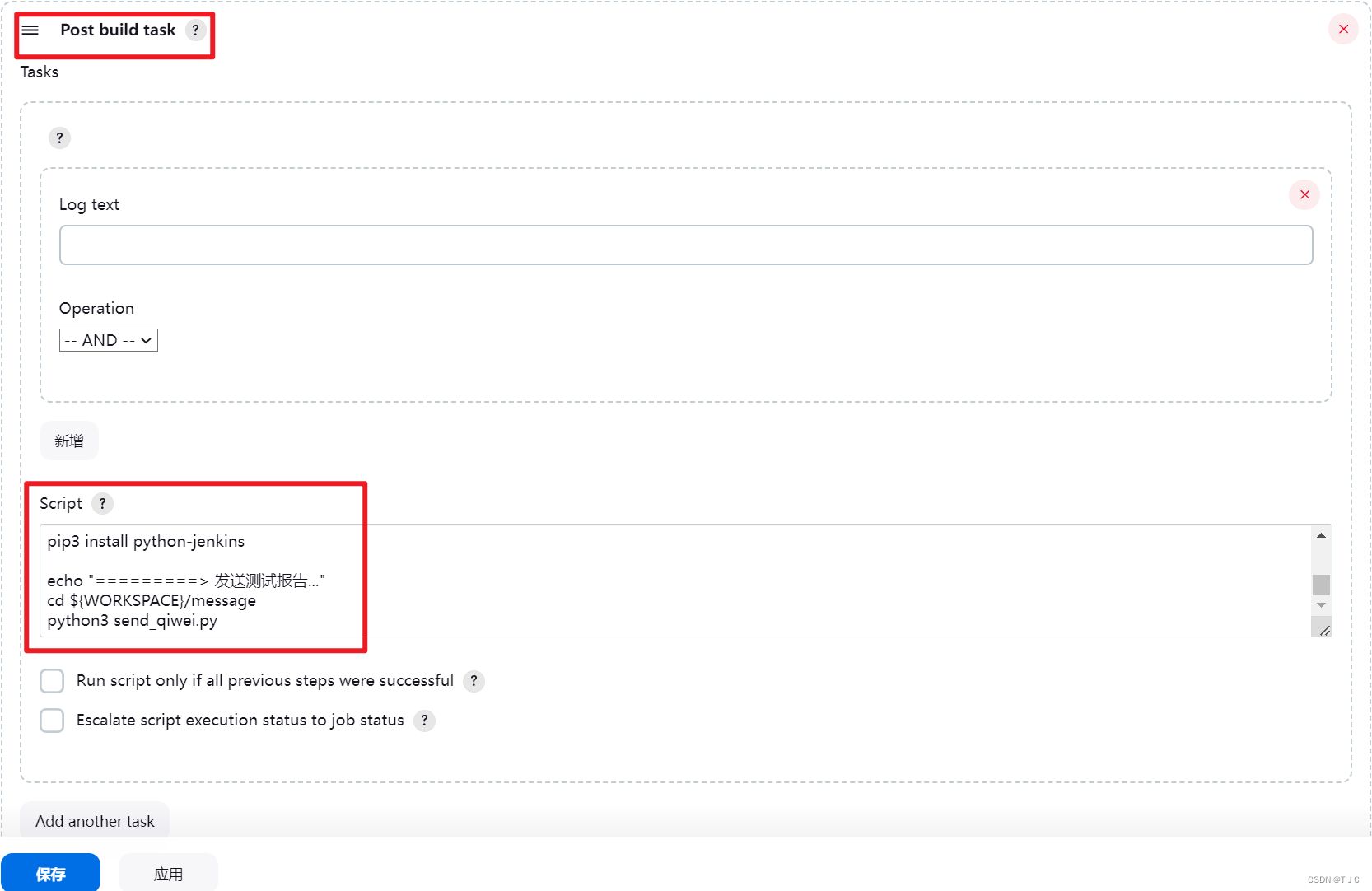
接口自动化之 + Jenkins + Allure报告生成 + 企微消息通知推送
接口自动化之 Jenkins Allure报告生成 企微消息通知推送 在jenkins上部署好项目,构建成功后,希望可以把生成的报告,以及结果统计发送至企微。 效果图: 实现如下。 1、生成allure报告 a. 首先在Jenkins插件管理中&#x…...

『Apisix安全篇』探索Apache APISIX身份认证插件:从基础到实战
🚀『Apisix系列文章』探索新一代微服务体系下的API管理新范式与最佳实践 【点击此跳转】 📣读完这篇文章里你能收获到 🛠️ 了解APISIX身份认证的重要性和基本概念,以及如何在微服务架构中实施API安全。🔑 学习如何使…...
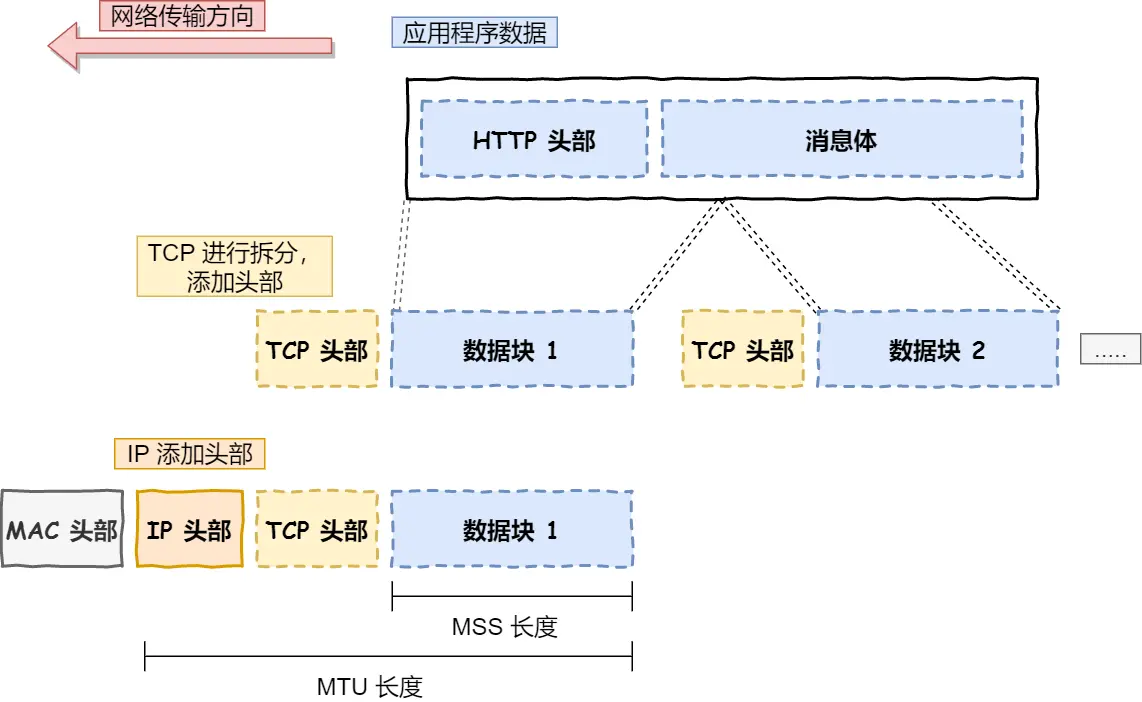
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了
【01-20】计算机网络基础知识(非常详细)从零基础入门到精通,看完这一篇就够了 以下是本文参考的资料 欢迎大家查收原版 本版本仅作个人笔记使用1、OSI 的七层模型分别是?各自的功能是什么?2、说一下一次完整的HTTP请求…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
