【4】单链表(有虚拟头节点)
【4】单链表(有虚拟头节点)
- 1、虚拟头节点
- 2、构造方法
- 3、node(int index) 返回索引位置的节点
- 4、添加
- 5、删除
- 6、ArrayList 复杂度分析
- (1) 复杂度分析
- (2) 数组的随机访问
- (3) 动态数组 add(E element) 复杂度分析
- (4) 动态数组的缩容
- (5) 复杂度震荡
- 7、单链表复杂度分析
- 8、完整代码
1、虚拟头节点
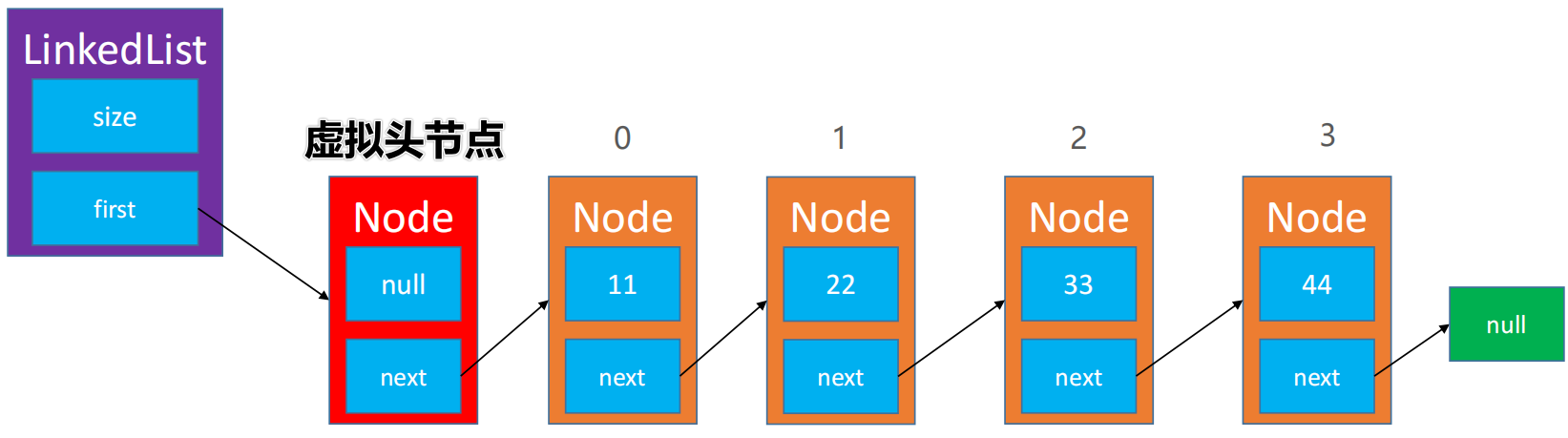
📕 为了让代码更精简,统一所有节点的处理逻辑,可以在最前面增加一个虚拟头节点
🖊 头指针指向的永远是虚拟头节点
🖊 虚拟头节点不存储数据
2、构造方法
📕 在 单链表 代码的基础上需要进行修改
🖊 头指针 first 永远指向虚拟头节点,所以在 VirtualHeadLinkedList 的构造方法中要让 first 指针虚拟头节点
public VirtualHeadLinkedList() {// 头指针指向虚拟头节点// 虚拟头节点的next默认指向nullfirst = new Node<>(null, null);}
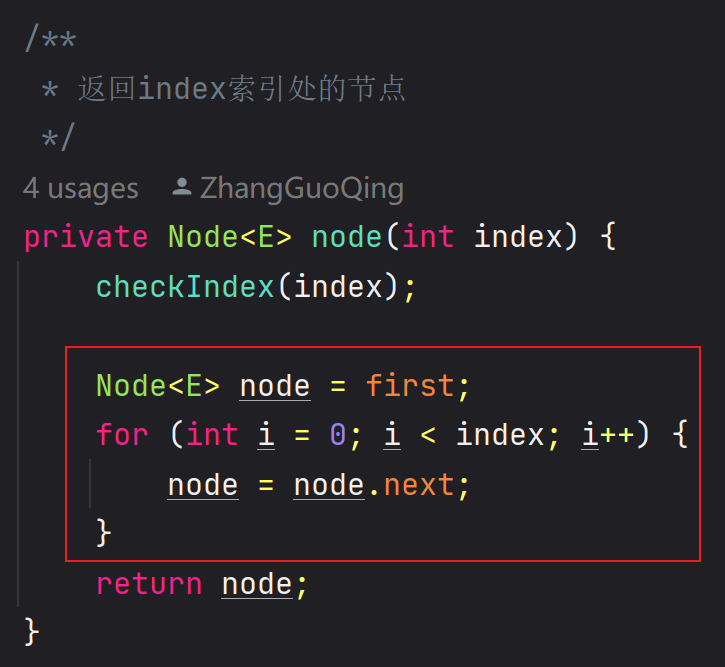
3、node(int index) 返回索引位置的节点
🖊 该方法会返回索引位置的节点,它原本的实现思路是:若需要
index位置的节点,则从first头指针指向的头节点开始 next index 次🖊 加入了虚拟头节点后,就不能从
first头指针指向的头节点开始 next index 次了,而是从虚拟头节点的 next 指向的节点开始next
/*** 返回index索引处的节点*/private Node<E> node(int index) {checkIndex(index);// first头指针指向的是虚拟头节点// first.next就是具体存储数据的第一个节点Node<E> node = first.next;for (int i = 0; i < index; i++) {node = node.next;}return node;}
4、添加
🖊 之前的添加逻辑:
① 假如是往头节点位置添加元素:first指向新节点,新节点的 next 指向之前的头节点
② 若不是往头节点位置添加元素:找到index-1索引处的节点prev,然后新节点的 next 指向prev.next,然后prev.next指向新节点
🖊 增加虚拟头节点后: 如果
index == 0,prev 就是虚拟头节点(first)
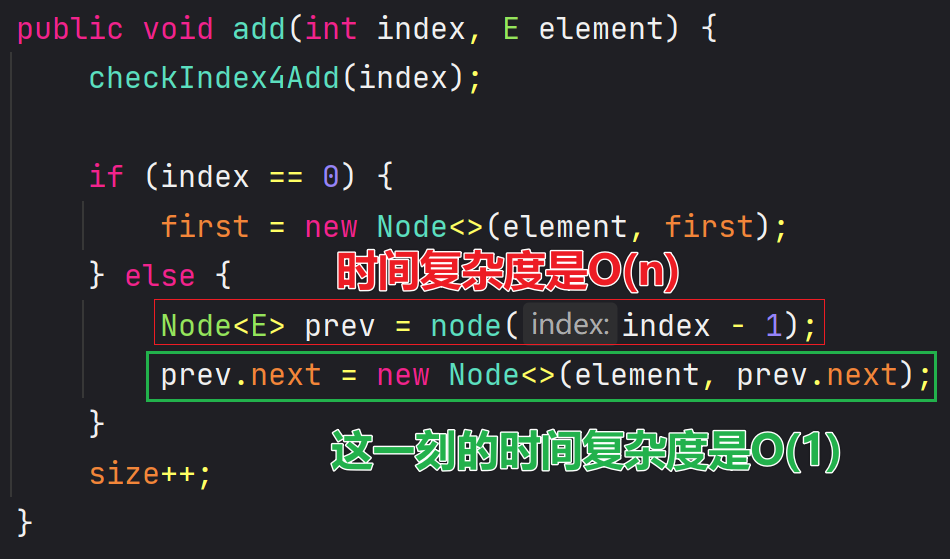
/*** 往索引位置添加元素*/@Overridepublic void add(int index, E element) {checkIndex4Add(index);// 如果index==0, prev是虚拟头节点Node<E> prev = (index == 0) ? first : node(index - 1);prev.next = new Node<>(element, prev.next);size++;}
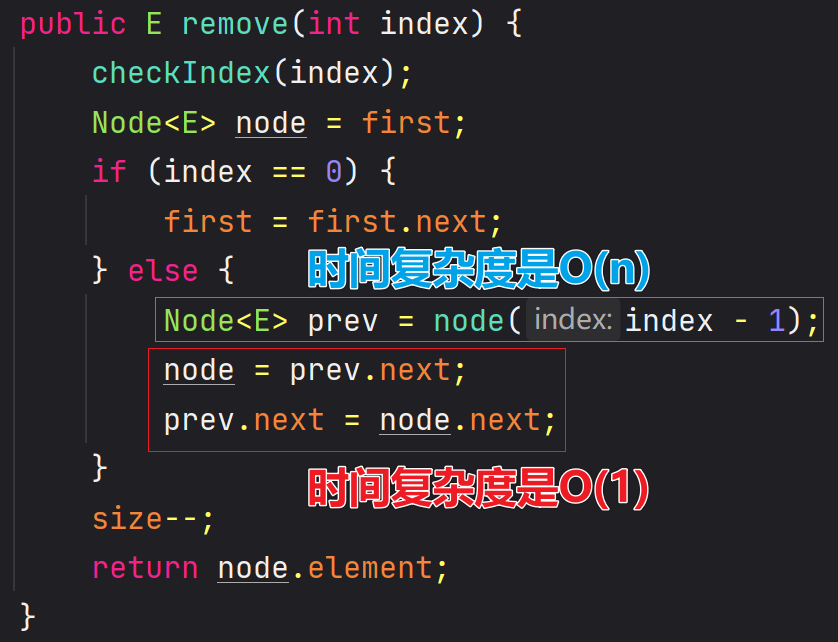
5、删除
🖊 假如删除的是
index == 0位置的节点,则prev就是虚拟头节点
/*** 删除索引位置的元素** @return 被删除的元素*/@Overridepublic E remove(int index) {checkIndex(index);Node<E> prev = (index == 0) ? first : node(index - 1);Node<E> node = prev.next;prev.next = node.next;size--;return node.element;}
6、ArrayList 复杂度分析
(1) 复杂度分析
◼ 最好情况复杂度
◼ 最坏情况复杂度
◼ 平均情况复杂度
| 方法 | 复杂度 |
|---|---|
get | O(1) |
set | O(1) |
add | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
remove | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
📕
add:
🖊 假如index == size(往最后面添加元素):无需挪动元素(时间复杂度是O(1))最好时间复杂度
🖊 假如index == 0:整个数组需要往后挪动(时间复杂度是O(n))最坏时间复杂度
🖊 平均时间复杂度:(1 + 2 + ... + n) / n = n/2【挪动1次、2次、...、 n次】
(2) 数组的随机访问
🖊 数组的随机访问速度非常快
🖊elements[n]的效率与 n 是多少无关
📕 假设存放的是 int 类型的元素(每个元素的地址相差四个字节):
🖊 地址值 = index * 4 + 数组首元素的地址
(3) 动态数组 add(E element) 复杂度分析
◼ 最好:O(1)
◼ 最坏:O(n)
◼ 平均:O(1)
◼ 均摊:O(1)
🖊
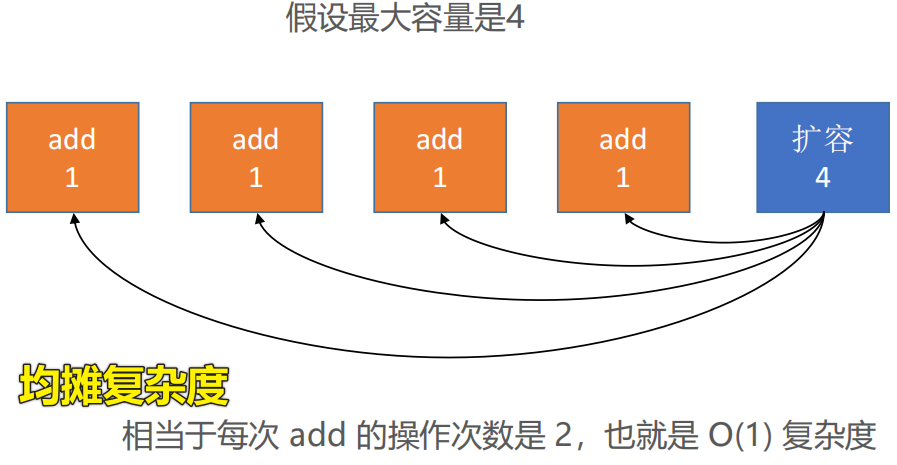
add(E element)永远是往数组的最后面添加元素,可能会有扩容的情况产生
🖊 扩容的时间复杂度是O(n)
🖊 但是该方法大部分情况下的时间复杂度都是O(1),只有极少数情况是O(n)【均摊复杂度】
📕 什么情况下适合使用均摊复杂度❓
🖊经过连续的多次复杂度比较低的情况后,出现个别复杂度比较高的情况
(4) 动态数组的缩容
📕 如果内存使用比较紧张,动态数组有比较多的剩余空间,可以考虑进行缩容操作
🖊 比如剩余空间占总容量的一半时,就进行缩容
/*** 缩容*/private void trim() {// 当前容量:elements数组最多可以存储的元素个数int curCap = elements.length;int newCap = curCap >> 1;if (size >= newCap || newCap <= DEFAULT_CAPACITY) return; // 不缩容E[] newElements = (E[]) new Object[newCap];// 把旧数组元素复制到新数组中for (int i = 0; i < size; i++) {newElements[i] = elements[i];}elements = newElements;System.out.println("🖊缩容:" + curCap + "→" + newCap);}
(5) 复杂度震荡
📕 如果扩容倍数、缩容时机设计不得当,有可能会导致复杂度震荡
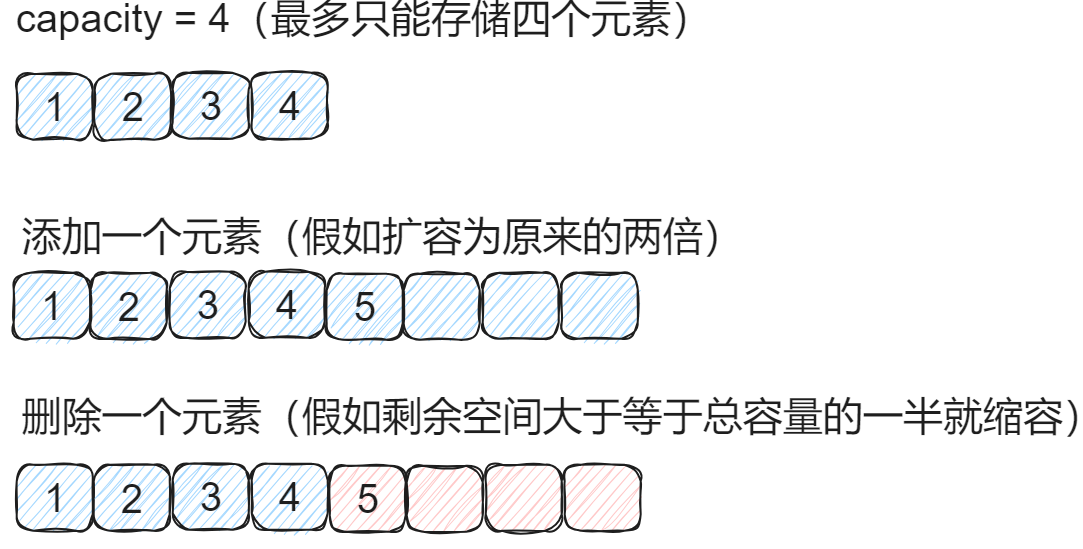
🖊 上图假如一直执行增、删、增、删、增、删…操作的话,就会出现扩容、缩容、扩容、缩容、扩容、缩容…的情况
🖊 出现此情况是因为:扩容为2倍(2)和剩余空间大于等于总容量一半(1/2)的时候缩容【扩容倍数和缩容时机的乘积不要等于1】
7、单链表复杂度分析
| 方法 | 复杂度 |
|---|---|
get | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
set | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
add | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
remove | ① 最好:O(1) ② 最坏:O(n) ③ 平均:O(n) |
🖊 单链表效率比较低主要是因为
node(int index)方法,它有 for 循环(数据规模可能是 n)
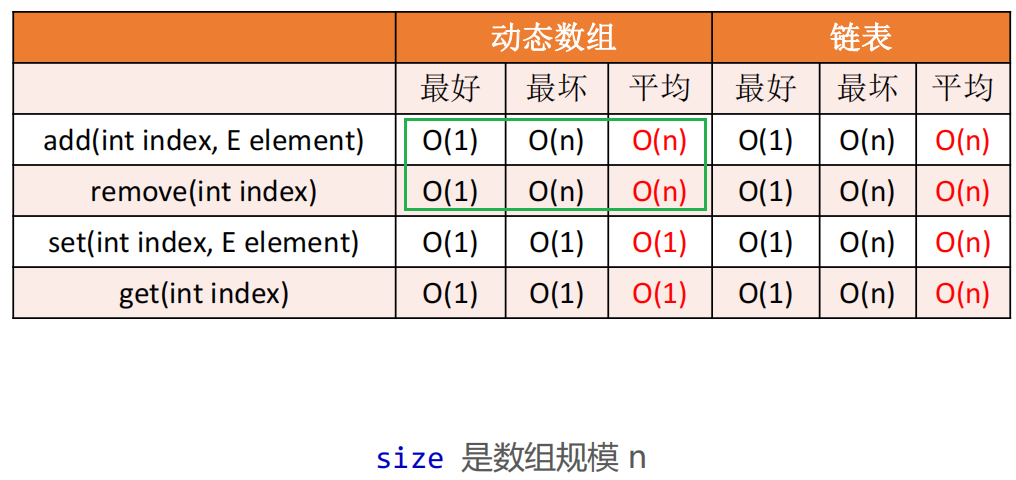
🖊 有的资料说链表添加和删除的复杂度是O(1),这说的是添加和删除的 “哪一刻”,但找到 prev 的时间复杂度可能是 O(n)
8、完整代码
🖊 带有虚拟头节点的单链表完整代码
相关文章:
【4】单链表(有虚拟头节点)
【4】单链表(有虚拟头节点) 1、虚拟头节点2、构造方法3、node(int index) 返回索引位置的节点4、添加5、删除6、ArrayList 复杂度分析(1) 复杂度分析(2) 数组的随机访问(3) 动态数组 add(E element) 复杂度分析(4) 动态数组的缩容(5) 复杂度震荡 7、单链…...

html第二次作业
骨架 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-width, initi…...
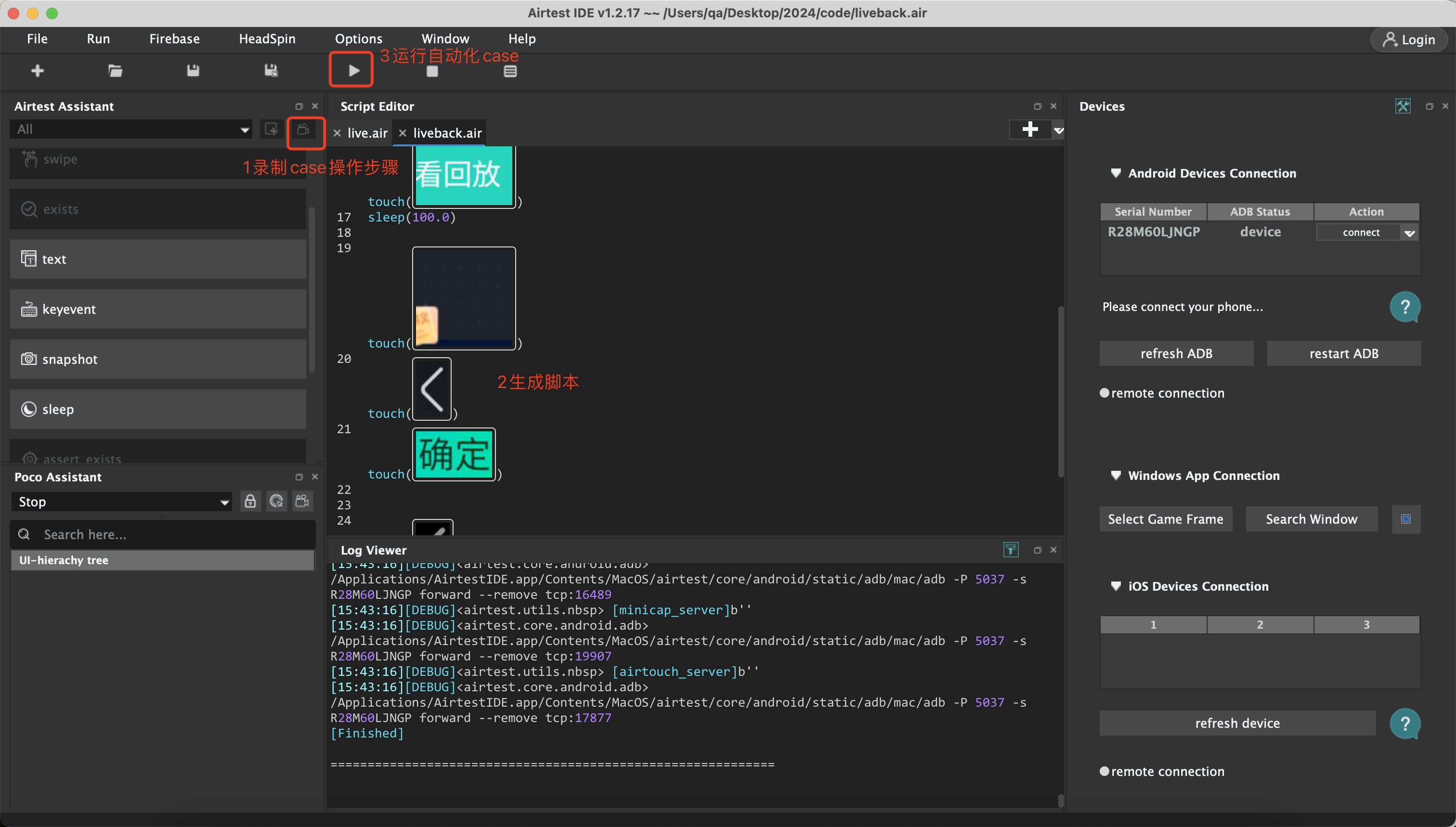
Android客户端自动化UI自动化airtest从0到1搭建macos+脚本设计demo演示+全网最全最详细保姆级有步骤有图
iOS客户端自动化UI自动化airtest从0到1搭建macosdemo演示-CSDN博客 一、基础环境 1. 安装jdk 选择jdk8 如果下载高版本 可能不匹配会失败 下载.dmg文件 苹果电脑 | macOS | jdk1.8 | 环境变量配置_jdk1.8 mac-CSDN博客 Java Downloads …...

基于单片机的自动浇灌系统的设计
本文设计了一款由单片机控制的自动浇灌系统。本设计的硬件电路采用AT89C51单片机作为主控芯片,采用YL-69土壤湿度传感器检测植物的湿度。通过单片机将采集湿度值与设定值分析处理后,控制报警电路和水泵浇灌电路的开启,从而实现植物的自动浇灌。 1 设计目的 随着生活水平的…...

WebStorm 与 VSCode 对比分析
WebStorm 与 VSCode 对比分析 1. 引言 简述WebStorm和VSCode的普及和重要性 WebStorm和Visual Studio Code(VSCode)是当前最受欢迎的代码编辑器之一,它们在现代软件开发中扮演着至关重要的角色。WebStorm,由JetBrains开发,是一个强大的IDE,特别受JavaScript开发者的欢…...

git命令-项目使用
项目中用到的git命令,记录下来,后续项目可以直接用 配置命令 一次性设置: git config --global user.name "Your Name" git config --global user.email "youremailaddress.com"git config --global alias.pl "pu…...
python安装删除以及pip的使用
目录 你无法想象新手到底会在什么地方出问题——十二个小时的血泪之言! 问题引入 python modify setup 隐藏文件夹 环境变量的配置 彻底删除python 其他零碎发现 管理员终端 删不掉的windous应用商店apps 发现问题 总结 你无法想象新手到底会在什么地方…...
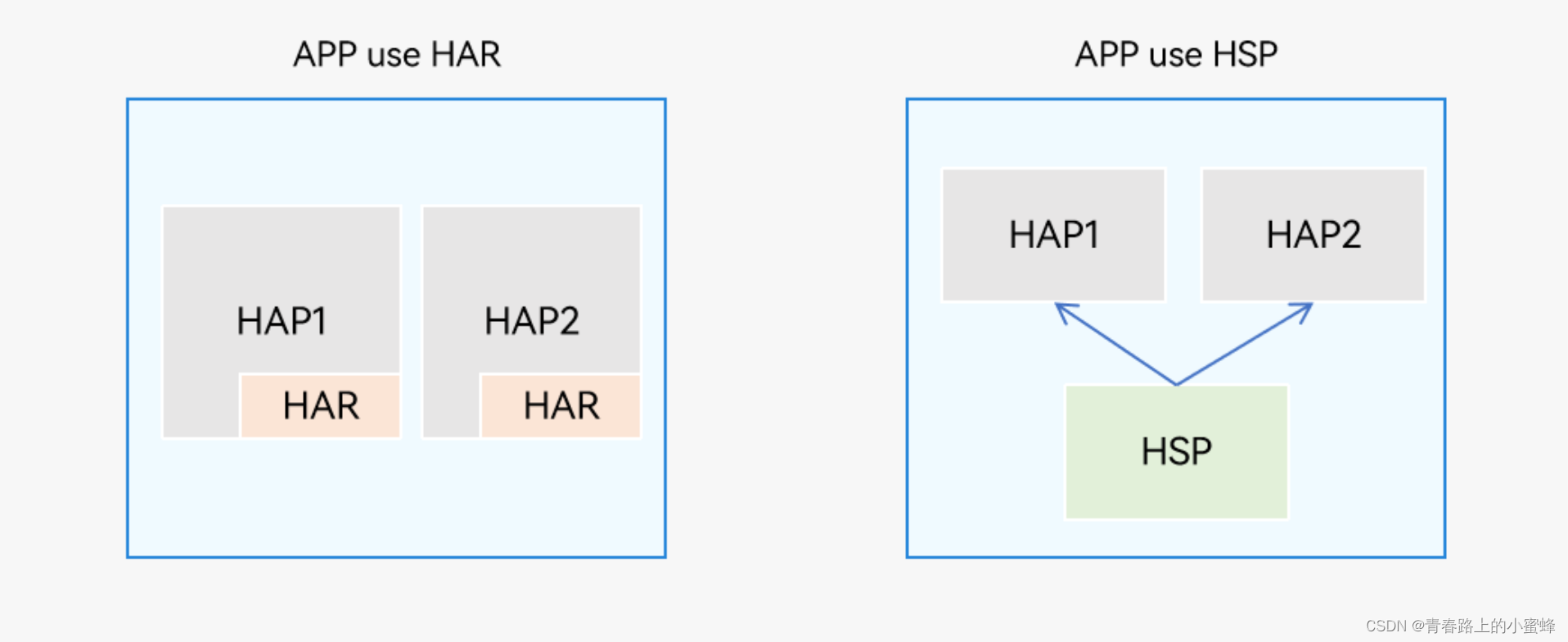
7、鸿蒙学习-共享包概述
HarmonyOS提供了两种共享包,HAR(Harmony Archive)静态共享包,和HSP(Harmony Shared Package)动态共享包。 HAR与HSR都是为了实现代码和资源的共享,都可以包含代码、C库、资源和配置文件…...

亚马逊测评新策略:解决底层环境防关联,提升下单成功率
对于做测评的环境系统,确保稳定性和成功率是非常重要的。市面上有各种环境方案,如虚拟机、模拟机、gcs、云手机、VPS等。然而,这些方案不仅成本高,而且成功率很低。因此,一个好的环境系统是成功的基础。 亚马逊平台的…...

容器和注解开发
1.创建容器的两种方式 //1.加载类路径下的配置文件//ApplicationContext ctx new ClassPathXmlApplicationContext("applicationContext.xml"); //2.从文件系统下加载配置文件(绝对路径) ApplicationContext ctx new FileSystemXmlApplicationContex…...
浏览器内置对象讲解之Dom篇)
有趣且重要的JS知识合集(21)浏览器内置对象讲解之Dom篇
1、Dom 1.1、概念 Document Object Model(文档对象模型), 整个WEB页面, 所有的Dom元素都在Document整个文档里。DOM就是把整个文档页面当做一个对象进行操作, document 下 包含了 根据 html 创建 的 Dom 对象, 这个DOM对象, 以树形结构展示, 即DOM树 …...
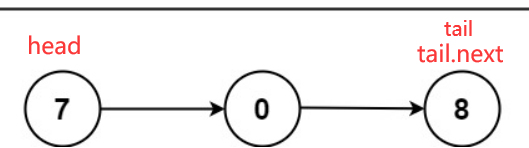
3.两数相加 - 链表
文章目录 题目简介题目解答代码: 题目链接 大家好,我是晓星航。今天为大家带来的是 两数相加 相关的讲解!😀 题目简介 题目解答 通过题目给的第一个示例来解析 图解如下: l1的2和l2的5首先相加变为7 这里相加结果为7…...
iptables 与 firewalld 防火墙
iptables iptables 是一款基于命令行的防火墙策略管理工具 四种防火墙策略: ACCEPT(允许流量通过) 流量发送方会看到响应超时的提醒,但是流量发送方无法判断流量是被拒绝,还是接收方主机当前不在线 REJECT(…...

Taskflow:异步任务(Asynchronous Tasking)
简单使用 tf::Executor 提供了异步执行Task的操作tf::Executor::async,并返回Future,用于保留该函数调用的结果。 #include <taskflow/taskflow.hpp>void print_str(char const* str) {std::cout << str << std::endl; }int main() …...

学习鸿蒙基础(9)
目录 一、鸿蒙国际化配置 二、鸿蒙常用组件介绍 三、鸿蒙像素单位介绍 四、鸿蒙布局介绍 1、Row与Column线性布局 2、层叠布局-Stack 3、弹性布局 4、栅格布局 5、网格布局 一、鸿蒙国际化配置 base目录下为默认的string。en_US对应美国的。zh_CN对应中国的。新增一个s…...

spring boot的小数位丢失.00 或者.0
1、背景 在使用spring boot时,前端的界面展示的数据是2 ,在数据库中存储的是小数。但是导出Excel的时候数据是 2.00 。奇了怪了为啥会不一样,数据都是一样的没有做过处理。 2、排查问题 经过层层的debug 发现数据库返回的数据是2.00&#x…...

nginx如何清理页面缓存
在 Nginx 中,清理页面缓存通常涉及配置缓存头以控制缓存行为,或者使用外部工具或机制来清除缓存。以下是一些建议来管理和清理 Nginx 的页面缓存: 配置缓存头: Nginx 本身不直接提供缓存机制,但可以通过配置 proxy_cac…...
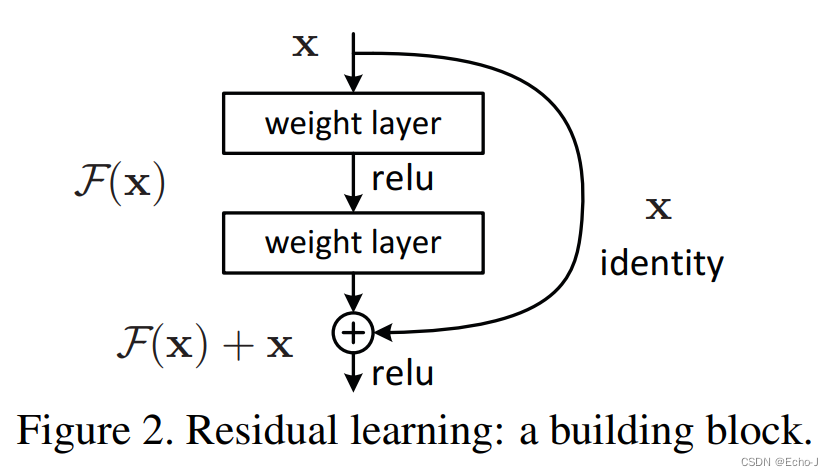
深度学习pytorch——经典卷积网络之ResNet(持续更新)
错误率前五的神经网络(图-1): 图-1 可以很直观的看到,随着层数的增加Error也在逐渐降低,因此深度是非常重要的,但是学习更好的网络模型和堆叠层数一样简单吗?通过实现表明(图-2&…...

react 面试题(2024 最新版)
1. 对 React 的理解、特性 React 是靠数据驱动视图改变的一种框架,它的核心驱动方法就是用其提供的 setState 方法设置 state 中的数据从而驱动存放在内存中的虚拟 DOM 树的更新 更新方法就是通过 React 的 Diff 算法比较旧虚拟 DOM 树和新虚拟 DOM 树之间的 Chan…...
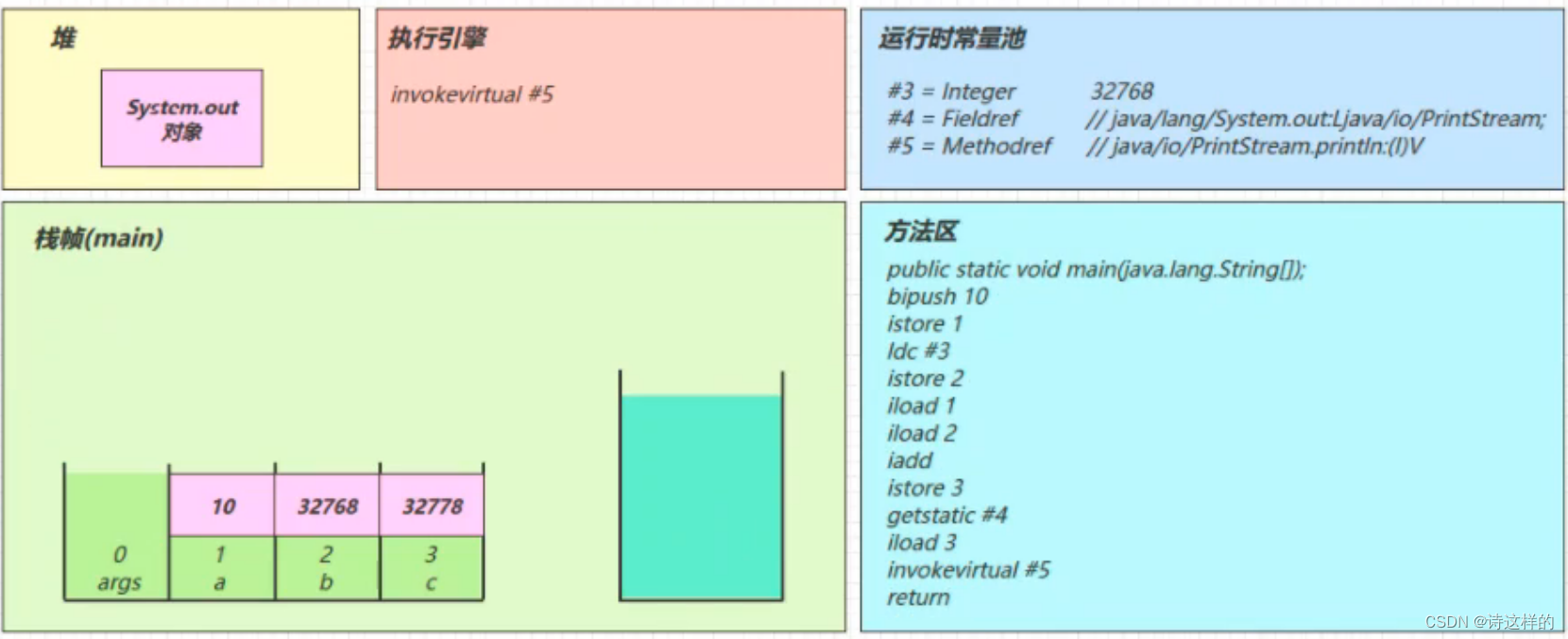
JVM(三)——字节码技术
三、字节码技术 1、类文件结构 一个简单的 HelloWorld.java package com.mysite.jvm.t5; // HelloWorld 示例 public class HelloWorld {public static void main(String[] args) {System.out.println("hello world");} }执行 javac -parameters -d . HellowWorld.…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...