蓝桥杯第七届大学B组详解
目录
1.煤球数量;
2.生日蜡烛;
3.凑算式
4.方格填数
5.四平方和
6.交换瓶子
7.最大比例
1.煤球数量

题目解析:可以根据·题目的意思,找到规律。
1 *- 1个
2 *** 3个
3 ****** 6个
4 ********** 10个
不难发现 第一层的个数加上第二层的层数就是第二层的煤球数目。本质就是找规律数学。
#include <iostream>
#include<vector>
using namespace std;int main()
{int n = 0, sum = 0;for(int i = 1; i <= 100; i++){n += i;sum += n;}cout << sum << endl;return 0;
}2.生日蜡烛

题目解析:直接枚举就行;
#include<iostream>
using namespace std;
int main()
{for (int i = 1;i <= 100; i++){int sum = 0;for (int j = i; j <= 100; j++){sum += j;if (sum == 236)cout << i << endl;}}return 0;
}3.凑算式

题目解析:是不是和三羊献瑞有点像,又可以使用next_premutation();
注意这个题目弄错了是1-9数字;md我就整整调试1个多小时,心态差点崩溃了,都开始怀疑自己了。
using namespace std;
#include<iostream>
#include<algorithm>int ret = 0;
int a[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9};bool check()
{int x = a[3] * 100 + a[4] * 10 + a[5];int y = a[6] * 100 + a[7] * 10 + a[8];if(((a[1] * y) + (a[2] * x)) % (a[2] * y) == 0 && a[0] + ((a[1] * y) + (a[2] * x)) / (a[2] * y) == 10){return true;}else{return false;}
}int main()
{do{if(check()){ret++;}}while(next_permutation(a, a + 9));cout << ret << endl;return 0;
}4.方格填数

题目解析:动态规划类型题目,就是在方格中填数,如果这个方格没有被使用过并且方格相邻不重复就将数字填进去,填完就是一种方案数。累计方案数。
细节:初始化为-20,因为如果为填9就算相邻区分不出来。
#include <iostream>
#include<bits/stdc++.h>
using namespace std;//方格矩阵,因为要使用到相邻的元素所以就会使用到就多创建行列
// -20 -20 -20-20
// +--+--+--+
// | | | | -20
// +--+--+--+--+
// | | | | | -20
// +--+--+--+--+
// | | | | -20
// +--+--+--+
//-20 -20 -20 -20 -20
int a[4][5];
//判断是否被使用过
int vis[10];
int sum = 0;
int dx[4] = {-1, -1, -1, 0};
int dy[4] = {0, 1, -1, -1};bool check(int x, int y, int num)
{for(int i = 0; i < 4; i++){int xx = dx[i] + x;int yy = dy[i] + y;//边界检查if(xx < 3 && xx >= 0 && yy < 4 && yy >= 0){//如果相邻的话那么相差一定为1;if(abs( a[xx][yy] - num ) == 1)return false;}}return true;
}void dfs(int x, int y)
{//出口:第二行第三列if(x == 2 && y == 3){sum++;return;}//开始填数for(int i = 0; i < 10; i++){//判断没被使用过的方格并且不相临if(vis[i] == 0 && check(x, y, i)){vis[i] = 1;a[x][y] = i;//递归下一个方格,或者下一行if(y + 1 < 4)dfs(x, y + 1);elsedfs(x + 1, 0);//回溯vis[i] = 0;}}
}int main()
{//矩阵初始for(int i = 0; i < 4; i++){for(int j = 0; j < 4; j++){a[i][j] = -20;}}//从第0行第一列开始;dfs(0,1);cout << sum << endl;return 0;
}5.四平方和

题目解析:可以想到暴力枚举的方法,复杂度为0(n^4)是非常恐怖的,那么就要想办法降低;就需要优化。
首先要知道 N= a*a + b*b + c*c + d*d;
那么 a 一定不会超过 N / 4; b 一定不会超过 N / 3; c 一定不会超过 N / 2;
d 一定不会超过 N;
其次我们可以先算 a 和 b,那么 N - a*a + b*b = c*c + d*d;
#include <iostream>
#include<map>
#include<cmath>
using namespace std;int main()
{//输入int N; cin >> N;map<int,int> exit;//c值存一下。for(int c = 0; c * c <= N / 2; c++){for(int d = c; c*c + d*d <= N; d++){if(exit.find(c * c + d * d) == exit.end())exit[c * c + d * d] = c;}}for(int a = 0; a * a <= N / 4; a++){for(int b = a; a*a + b*b <= N / 3; b++){if(exit.find(N - a * a - b * b) != exit.end()){int c = exit[N - a * a - b * b];int d = (int)sqrt(N - a*a - b*b - c*c);cout << a << b << c << d << endl;//找到直接返回return 0;}}}return 0;
}6.交换瓶子

题目解析:是不是会想到冒泡,但是你看看数据范围,那么就是肯定要优化;将当前元素与下标进行比较,如果相同直接跳过,不相同那么就要找到和下标相同的数据下标进行交换。
#include<iostream>using namespace std;
int a[10001];
int N;
int sum = 0;int pos(int x)
{for(int i = 1; i <= N; i++){if(a[i] == x){return i;}}return -1;
}void Swap(int i, int j)
{int tmp = a[i];a[i] = a[j];a[j] = tmp;
}int main()
{//数据处理;cin >> N;for(int i = 1; i <= N; i++){cin >> a[i];}//进行查寻for(int i = 1; i <= N; i++){if(a[i] == i)continue;else{//找到和下标不一样的数,和下标交换,不需要改变原来的值。Swap(pos(i), i);sum++;}}cout << sum << endl;return 0;
}7.最大比例

题目解析:本道题说到所有级别的奖金构成一个等比数列,先进行排序,将第一个数作为分母,分子分别都是后面的数,求取他们的最大公约数,再用两个数组将分子分母分别除以最大公约数,再存放起来。最后再对分子分母分别求差最小就会得到最终答案。
#include <iostream>
#include<algorithm>
using namespace std;#define N 100
long long max = 1000000000;
long long x[N], a[N], b[N];long long gcd(long long a, long long b)
{return b ? gcd(b, a % b) : a;
}long long gcd_sub(long long a, long long b)
{if(b == 1) return a;if(b > a) swap(a, b);return gcd_sub(b, a / b);
}int main()
{//输入完成:int n;cin >> n;for(int i = 0; i < n; i++){cin >> x[i];}//排序sort(x, x + n);long long dd;//求最大公约数int cnt = 0;for(int i = 1; i < n; i++){if(x[i] != x[i-1]) //去除为1的情况{dd = gcd(x[i], x[0]);a[cnt] = x[i] / dd; //分子b[cnt] = x[0] / dd; //分母cnt++;}}long long up = a[0], down = b[0];for(int i = 1; i < cnt; i++){up = gcd_sub(up, a[i]);down = gcd_sub(down, b[i]);}cout << up << "/" << down;return 0;
}其实静下心来感受会觉得题目不难,就是要找到规律,总结方法,写代码注意细节,那么绝对可以取得高分。
相关文章:

蓝桥杯第七届大学B组详解
目录 1.煤球数量; 2.生日蜡烛; 3.凑算式 4.方格填数 5.四平方和 6.交换瓶子 7.最大比例 1.煤球数量 题目解析:可以根据题目的意思,找到规律。 1 *- 1个 2 *** 3个 3 ****** 6个 4 ********** 10个 不难发现 第…...

荣誉 | 人大金仓连续三年入选“金融信创优秀解决方案”
3月28日,由中国人民银行领导,中国金融电子化集团有限公司牵头组建的金融信创生态实验室发布“第三期金融信创优秀解决方案”,人大金仓新一代手机银行系统解决方案成功入选,这也是人大金仓金融行业解决方案连续第三年获得用户认可。…...
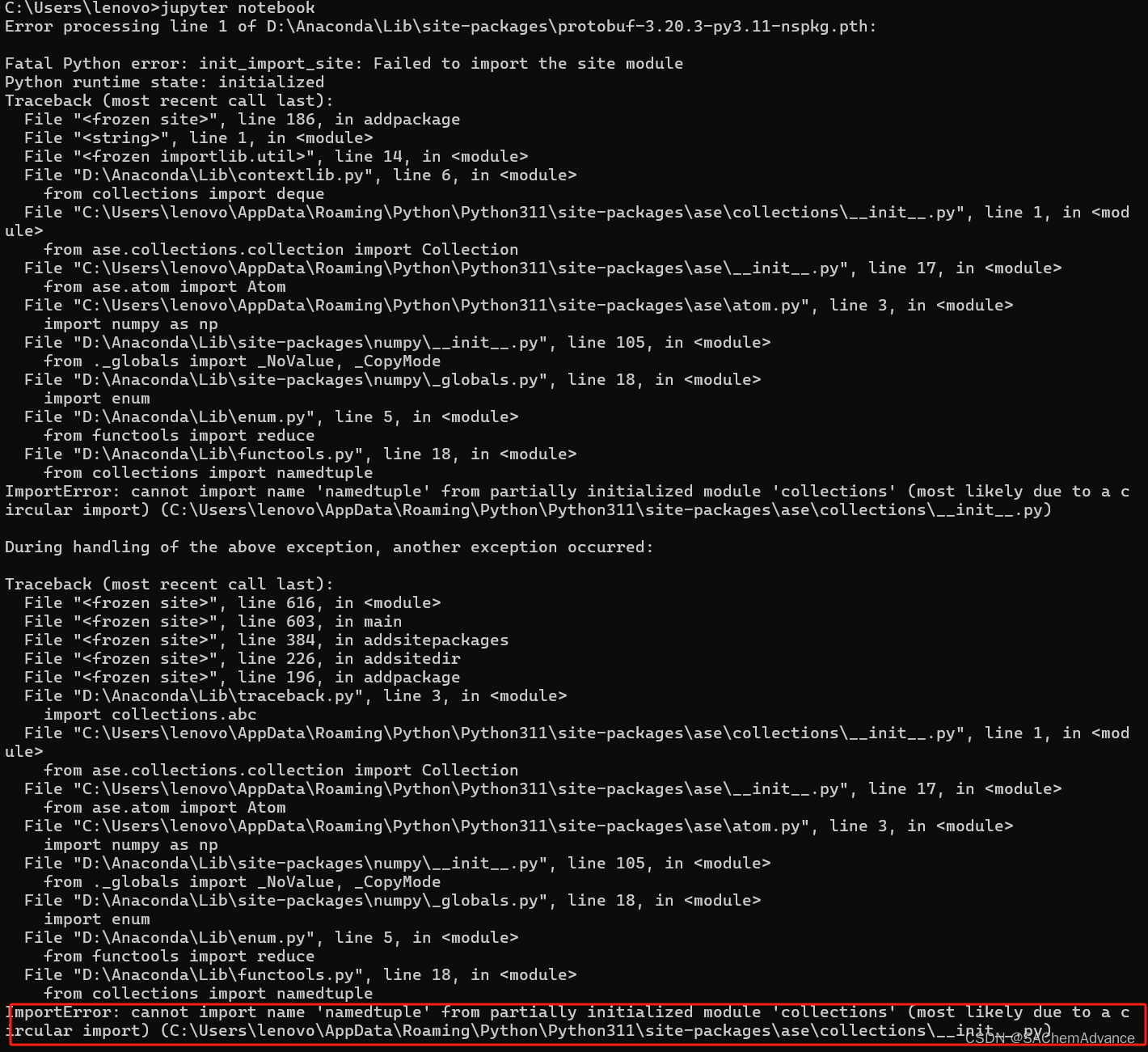
【关于jupyter notebook】一打开就闪退的问题
在Anaconda Prompt中输入jupyter notebook发现是有个错误。 里面多了一个__init__.py的文件导致报错。删除之后,就可以使用了...
若依 3.8.7版本springboot前后端分离 整合mabatis plus
1.去掉mybatis 这一步我没有操作,看别人的博客有说不去掉可能冲突,也可能不冲突,我试下来就没去掉如需要去除,到总的pom.xml中properties标签下的<mybatis-spring-boot.version>x.x.x</mybatis-spring-boot.version>…...

vue做移动端自适应插件实现rem
1.实现方式 postcss-pxtorem:将px转换为rem amfe-flexible:为html、body提那家font-size,窗口调整的时候重新设置font-size 2.安装与使用 npm install amfe-flexible --save npm install postcss-pxtorem --save-dev 1.再main.js入口文件…...
)
android 快速实现 图片获取并裁剪(更换头像)
1.获取图片框架:https://github.com/LuckSiege/PictureSelector 2.图片裁剪框架:https://github.com/jdamcd/android-crop 3.Glide图片加载框架:https://github.com/bumptech/glide 2.build.gradle依赖: dependencies {// Pic…...

垃圾回收机制--GC 垃圾收集器--JVM调优-面试题
1.触发垃圾回收的条件 新生代 Eden区域满了,触发young gc (ygc)老年代区域满了,触发full gc (fgc)通过ygc后进入老年代的平均大小大于老年代的可用内存,触发full gc(fgc).程序中主动调用的System.gc()强制执行gc,是full gc,但是不必然执行。…...
)
Java基础知识总结(29)
Java虚拟机 运行时数据区 程序计数器 方法区:Java 8以后没有方法区,改为了元空间(MetaSpace) 虚拟机栈 堆 本地方法栈 程序计数器 它可以看作是当前线程所执行的字节码的行号指示器。在Java虚拟机的概念模型里,…...

vue js金额转中文
在Vue.js项目中,实现金额转中文的功能通常涉及编写一个JavaScript方法来处理数字转换逻辑,并在Vue组件中调用该方法。下面是一个基本的示例,展示如何在Vue组件中定义一个计算属性或方法来实现这一功能: /*** 思路: …...
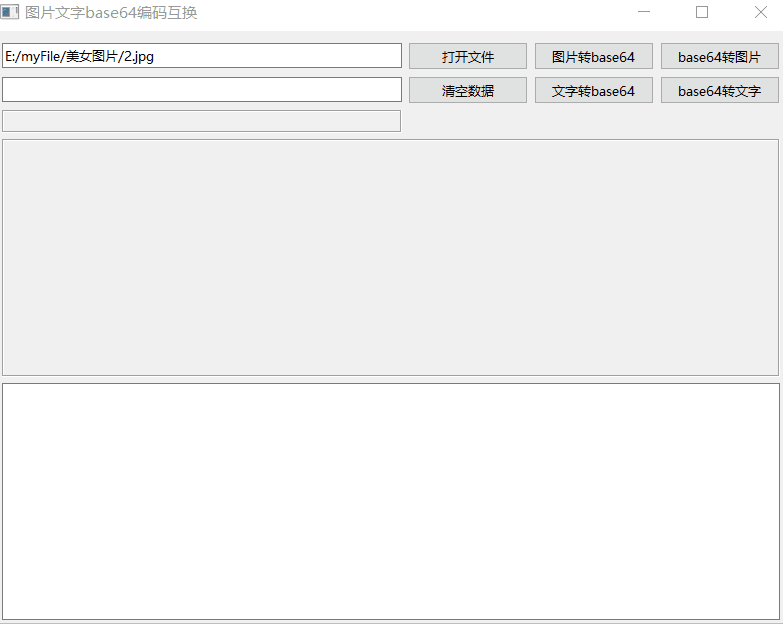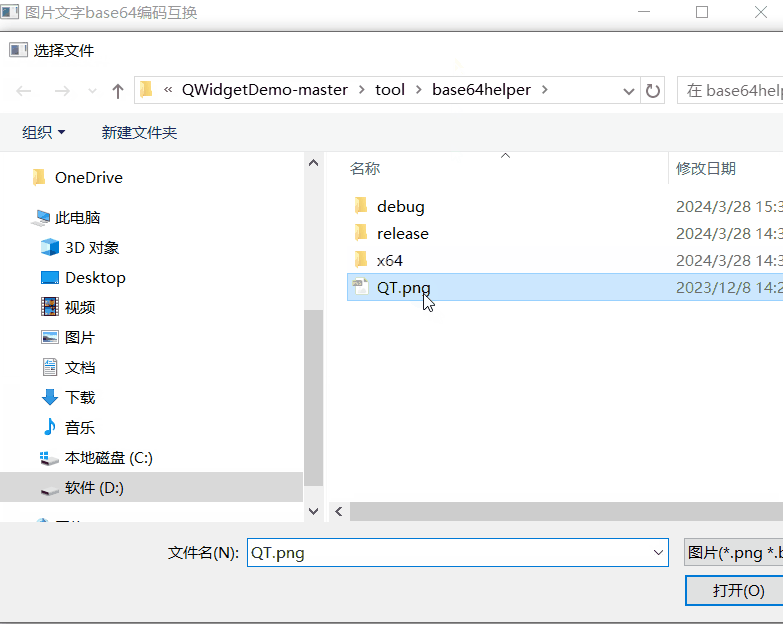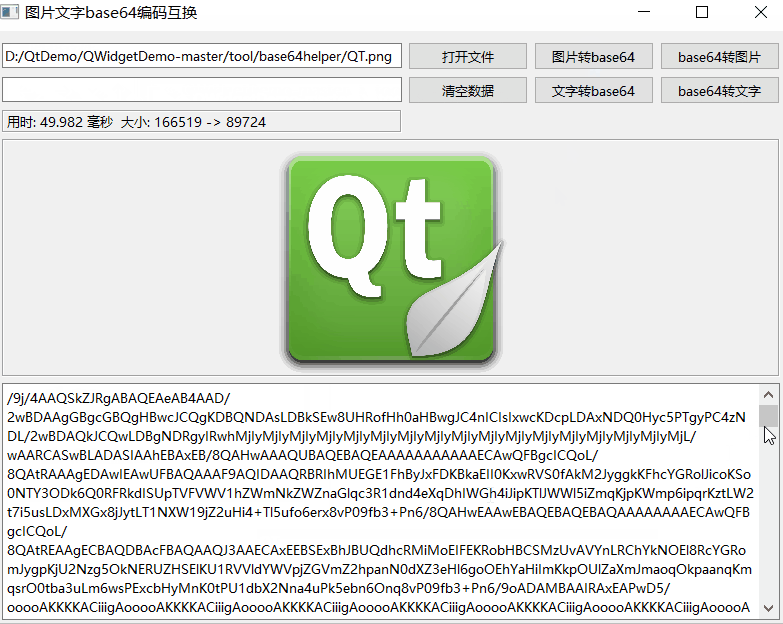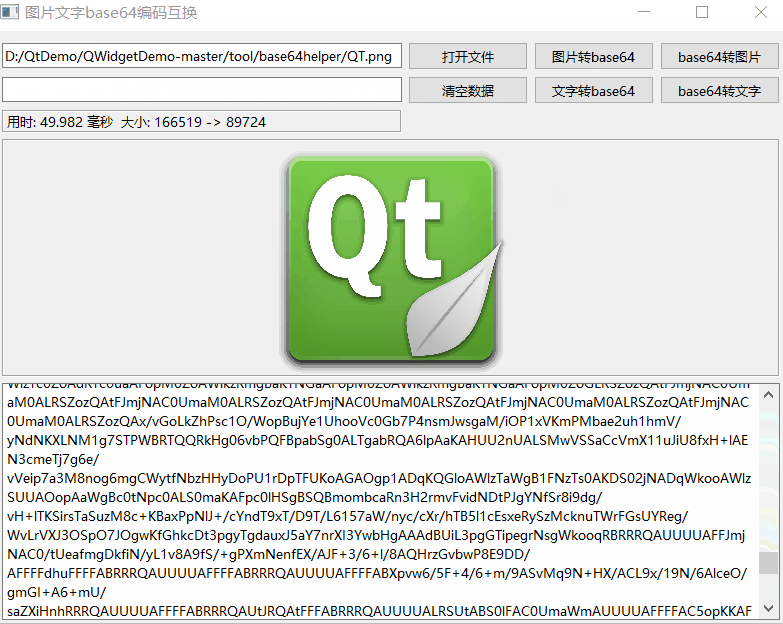
《QT实用小工具·二》图片文字转base64编码
1、概述 源码放在文章末尾 base64编码转换类 图片转base64字符串。base64字符串转图片。字符转base64字符串。base64字符串转字符。后期增加数据压缩。Qt6对base64编码转换进行了重写效率提升至少200%。 下面是demo演示: 项目部分代码如下所示: #ifn…...
Django安装及第一个项目
1、安装python C:\Users\leell>py --version Python 3.10.6 可以看出我的环境python的版本3.10.6,比较新 2、 Python 虚拟环境创建 2.1 官网教程 目前,有两种常用工具可用于创建 Python 虚拟环境: venv 在 Python 3.3 及更高版本中默…...

专升本-物联网
物联网(IOT,Internet of things) 体系结构: 感知层(感知执行层) 网络层 应用层 基本特征: 全面感知 可靠传输 智能处理 作用: 信息采集、转换、收集 信息传递和处理 数据…...

二叉树的遍历C语言
二叉树作为FDS课程最核心的数据结构之一,要求每个人都掌握! 这是一道简单的二叉树问题! 我们将给出一颗二叉树,请你输出它的三种遍历,分别是先序遍历,中序遍历,后序遍历! 输入格式…...
PostgreSQL到Doris的迁移技巧:实时数据同步新选择!
PostgreSQL可以说是目前比较抢手的关系型数据库了,除了兼具多样功能和强大性能之外,还具备非常优秀的可扩展性,更重要的是它还开源,能火不是没有理由的。 虽然PostgreSQL很强大,但是它也有短板,相对于专业…...
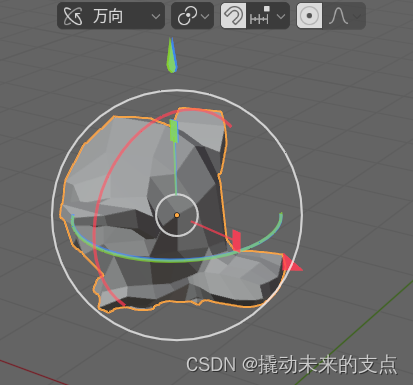
【三维】关于万向节锁的直白解释
1. 分析理解 万向节长什么样子,请参考这篇文章中的图片:https://zhuanlan.zhihu.com/p/42519819。 看了很多篇解释性的文章,没怎么看懂。因为我个人最关注的问题点在于: 现实物体旋转为什么没有所谓的万向节锁的bug,…...

程序员的修养 - 变量
变量几乎代码程序程序 中最基础的组成单元,程序员几乎无时无刻都在接触变量。但你对变量的理解真的足够吗? 首先,什么是变量?! 第一层理解:一个可以改变的量,区别于常量,用户可以修…...
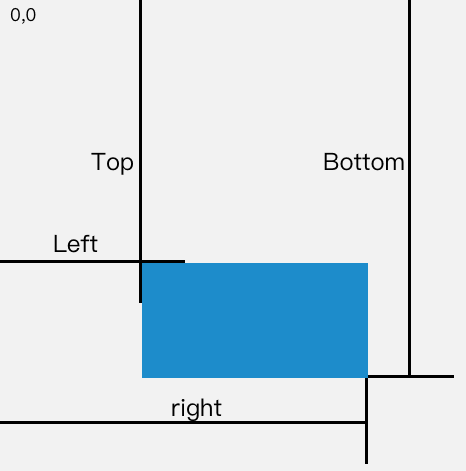
判断一个元素是否在可视区域中
文章目录 一、用途二、实现方式offsetTop、scrollTop注意 getBoundingClientRectIntersection Observer创建观察者传入被观察者 三、案例分析 参考文献 一、用途 可视区域即我们浏览网页的设备肉眼可见的区域,如下图 在日常开发中,我们经常需要判断目标…...
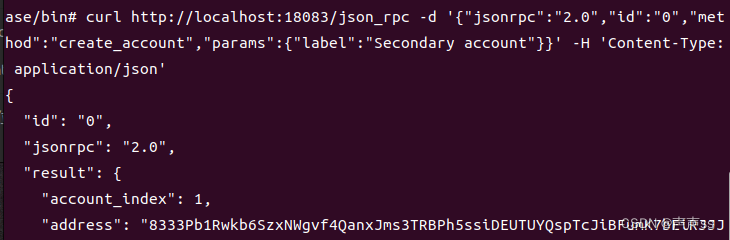
【Monero】Wallet RPC | Wallet CLI | 门罗币命令行查询余额、种子、地址等命令方法教程
ubuntu22.04 首先在运行daemon,详细安装运行教程可参考:The Monero daemon (monerod) ./monerodWallet CLI run ./monero-wallet-cli如果还没有钱包就根据提示创建钱包即可 输入密码 查询余额 balance查询种子 seed其他可执行命令操作࿱…...

FPGA----ZCU106的petalinux 2019.1使用USB传输数据
1、实际项目中需要用到开发板的串口进行数据交互,之前讲的几节只是启动了网口(如下链接)。因此,本次给大家带来的官方自带串口例程的使用方法,本文的vivado工程和下述连接一样,PL端什么配置都没有。 FPGA-…...
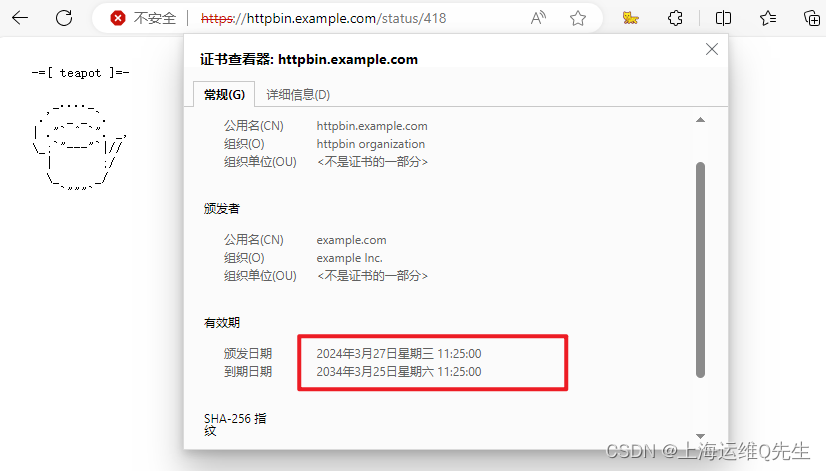
备考ICA----Istio实验10---为单个主机配置TLS Istio Ingress Gateway实验
备考ICA----Istio实验10—为单个主机配置 TLS Istio Ingress Gateway实验 1. 环境准备 部署httpbin kubectl apply -f istio/samples/httpbin/httpbin.yaml 2. 证书生成 2.1 生成根证书 生成根证书keyfile和crt文件 mkdir example_certs_root openssl req -x509 -sha256 …...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...
