每日OJ题_子序列dp⑧_力扣446. 等差数列划分 II - 子序列
目录
力扣446. 等差数列划分 II - 子序列
解析代码
力扣446. 等差数列划分 II - 子序列
446. 等差数列划分 II - 子序列
难度 困难
给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。
如果一个序列中 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该序列为等差序列。
- 例如,
[1, 3, 5, 7, 9]、[7, 7, 7, 7]和[3, -1, -5, -9]都是等差序列。 - 再例如,
[1, 1, 2, 5, 7]不是等差序列。
数组中的子序列是从数组中删除一些元素(也可能不删除)得到的一个序列。
- 例如,
[2,5,10]是[1,2,1,2,4,1,5,10]的一个子序列。
题目数据保证答案是一个 32-bit 整数。
示例 1:
输入:nums = [2,4,6,8,10] 输出:7 解释:所有的等差子序列为: [2,4,6] [4,6,8] [6,8,10] [2,4,6,8] [4,6,8,10] [2,4,6,8,10] [2,6,10]
示例 2:
输入:nums = [7,7,7,7,7] 输出:16 解释:数组中的任意子序列都是等差子序列。
提示:
1 <= nums.length <= 1000-2^31 <= nums[i] <= 2^31 - 1
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {}
};解析代码
和力扣873. 最长的斐波那契子序列的长度、力扣1027. 最长等差数列类似,动态规划解法思路:
状态表示:以某个位置为结尾,结合题目要求,先定义一个状态表示:
dp[i] 表示:以 i 位置元素为结尾的所有子序列中,等差数列的个数。
但是这里有⼀个非常致命的问题,那就是我们无法确定 i 结尾的斐波那契序列的样子。这样就会导致我们无法推导状态转移方程,因此我们定义的状态表示需要能够确定一个等差数列
根据等差数列的特性,我们仅需知道序列里面的最后两个元素,就可以确定这个序列的样子。因此,修改状态表示为:
dp[i][j] 表示:以 i 位置以及 j 位置的元素为结尾的所有的子序列中,等差数列的个数。规定一下 i < j 。
状态转移方程:
设 nums[i] = b, nums[j] = c ,那么这个序列的前一个元素就是 a = 2 * b - c。根据 a 的情况讨论:
- a 存在,下标为 k ,并且 a < b :此时我们需要以 k 位置以及 i 位置元素为结尾的等差数列的长度,然后再加上 j 位置的元素(+1)即可。于是 dp[i][j] =dp[k][i] + 1 ; 因为 a 可能有很多个,我们需要全部累加起来。p[i][j] +=dp[k][i] + 1 ;
- a 存在,但是 b < a < c :dp[i][j] =0 ;
- a 不存在: dp[i][j] = 0 ;
综上,状态转移方程分情况讨论即可。
优化点:我们发现,在状态转移方程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之前,将所有的元素和下标数组绑定在⼀起,放到哈希表中。这里为什么保存下标数组,是因为要统计个数,所有的下标都需要统计。
初始化:可以将表里面的值都初始化为 0 。
填表顺序:先固定斐波那契子序列的最后一个数,然后枚举倒数第二个数。
返回值:返回 dp 表中的所有值的和。
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size(), ret = 0;vector<vector<int>> dp(n, vector<int>(n, 0));// dp[i][j] 表示:以 i 位置以及 j 位置的元素为结尾的所有的子序列中,等差数列的个数。i < j unordered_map<long long, vector<int>> hash(n);for(int i = 0; i < n; ++i){hash[nums[i]].push_back(i);}for(int j = 2; j < n; ++j) // 固定倒数第一个数{for(int i = 1; i < j; ++i) // 先固定倒数第二个数{long long a = (long long)2 * nums[i] - nums[j]; // 防溢出if(hash.count(a)){for(auto& k : hash[a]){if(k < i)dp[i][j] += dp[k][i] + 1;elsebreak;}}ret += dp[i][j];}}return ret;}
};相关文章:

每日OJ题_子序列dp⑧_力扣446. 等差数列划分 II - 子序列
目录 力扣446. 等差数列划分 II - 子序列 解析代码 力扣446. 等差数列划分 II - 子序列 446. 等差数列划分 II - 子序列 难度 困难 给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。 如果一个序列中 至少有三个元素 ,并且任意两个相邻…...

GOPROXY 代理设置
通常报错: 1.http: server gave HTTP response to HTTPS client 2.timeout 解决指令:(会话临时性),长久的可以在配置文件中配置 go env -w GOPROXYhttps://goproxy.cn,direct 长久的,在~/.bashrc文件中添加: expo…...

Redis面经
Redis面经 Redis缓存穿透、缓存击穿和缓存雪崩及解决方案概述缓存穿透详解及解决方案缓存击穿详解及解决方案缓存雪崩详解及解决方案 Redis持久化机制什么是数据持久化?Redis数据持久化概述RDB持久化的优缺点AOF持久化混合持久化 Redis缓存穿透、缓存击穿和缓存雪崩…...
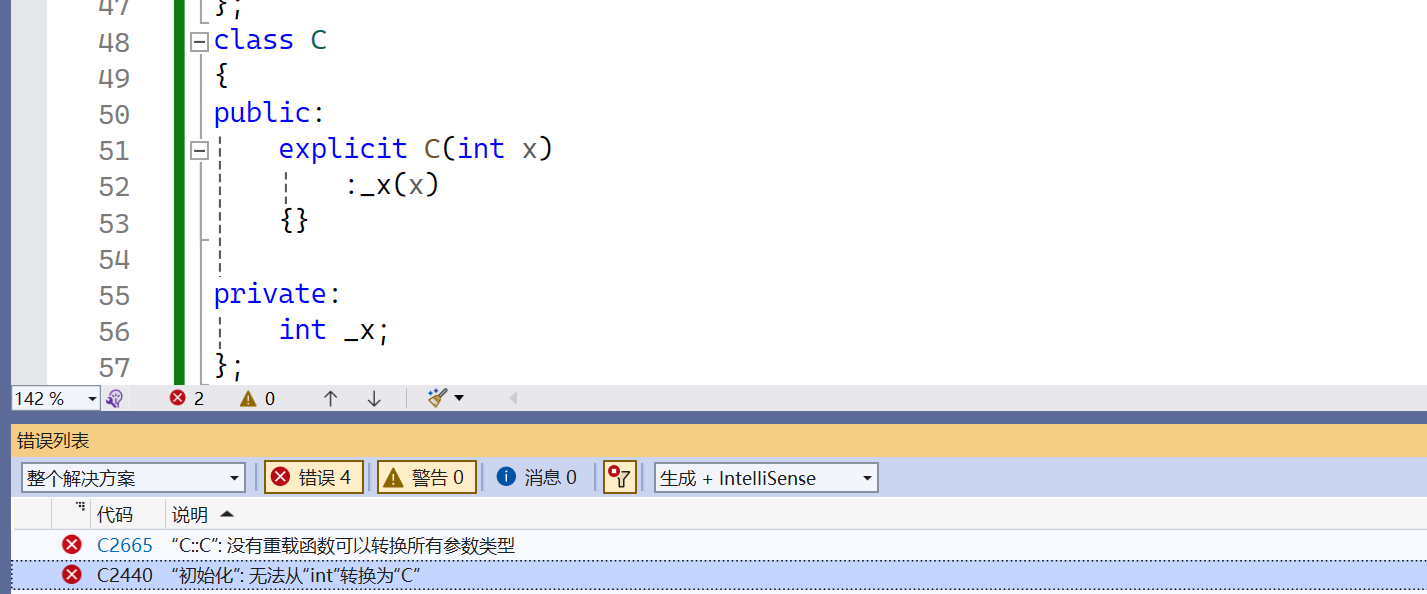
【c++】类和对象(六)深入了解隐式类型转换
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章我们来到初始化列表,隐式类型转换以及explicit的内容 目录 1.初始化列表1.1构造函数体赋值1.2初始化列表1.2.1隐式类型转换与复制初始化 1.3e…...

什么是nginx正向代理和反向代理?
什么是代理? 代理(Proxy), 简单理解就是自己做不了的事情或实现不了的功能,委托别人去做。 什么是正向代理? 在nginx中,正向代理指委托者是客户端,即被代理的对象是客户端 在这幅图中,由于左边内网中…...

【Go】面向萌新的Gin框架知识梳理学习笔记
目录 Gin框架简介 路由&路由组 1. 定义基本路由 2. 参数传递 3. 查询字符串参数 4. 路由组 5. 路由中间件 模板渲染 1. 加载模板 2. 定义模板 3. 渲染模板 4. 自定义模板函数 返回json 1. 导入 Gin 包 2. 创建 Gin 引擎 3. 定义路由和处理器函数 4. 运行服…...

baseDao增删改查.
这里写目录标题 1、baseDao增删改查介绍2、basDao类3、BasDao类的作用 1、baseDao增删改查介绍 (1)、增加Create)操作: 通过BaseDao的insert方法可以向数据库中插入一条新的记录。 该方法接受一个实体对象作参数,将该对象的属性映射到表的字…...

什么是面向对象【大白话Java面试题】
什么是面向对象 同样是解决一个问题,面向对象的角度是将问题抽象成对象的形式。通过分类的思维方式,将问题分成几个解决方案的对象。给每个对象赋值属性和方法,对每个对象的细节进行面向过程的思维,执行自己的方法来解决问题。 …...
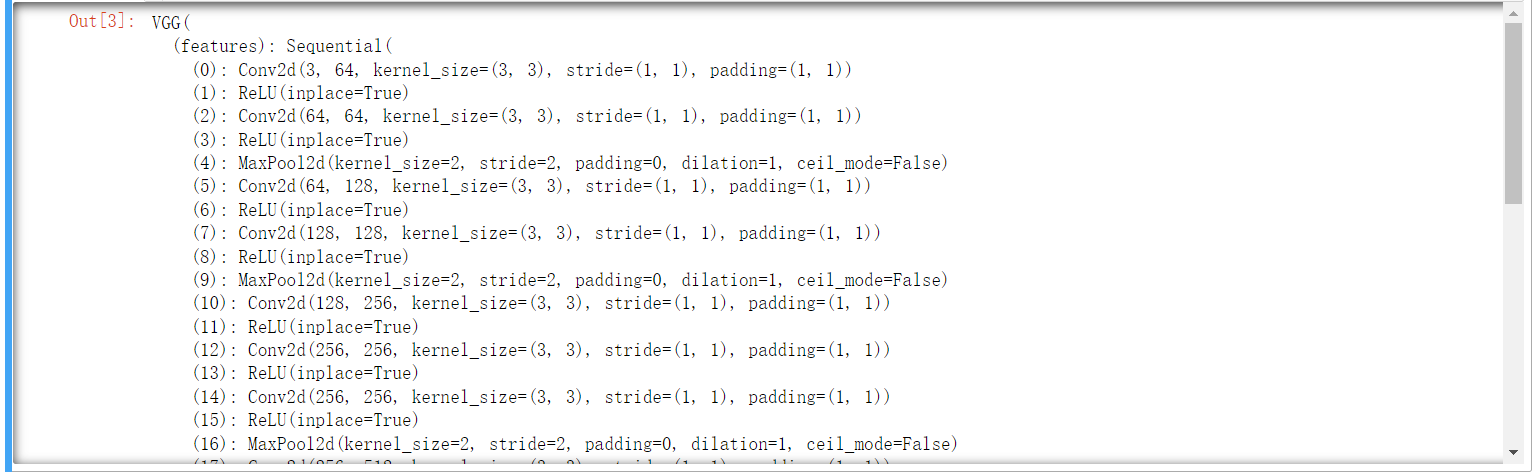
PyTorch 教程-快速上手指南
文章目录 PyTorch Quickstart1.处理数据2.创建模型3.优化模型参数4.保存模型5.加载模型 PyTorch 基础入门1.Tensors1.1初始化张量1.2张量的属性1.3张量运算1.3.1张量的索引和切片1.3.2张量的连接1.3.3算术运算1.3.4单元素张量转变为Python数值 1.4Tensor与NumPy的桥接1.4.1Tens…...

【有芯职说】数字芯片BES工程师
一、 数字芯片BES工程师简介 今天来聊聊数字芯片BES工程师,其中BES是Back End Support的缩写,就是后端支持的意思。其实这个岗位是数字IC前端设计和数字IC后端设计之间的一座桥,完成从寄存器传输级设计到具体工艺的mapping和实现。这个岗位在…...
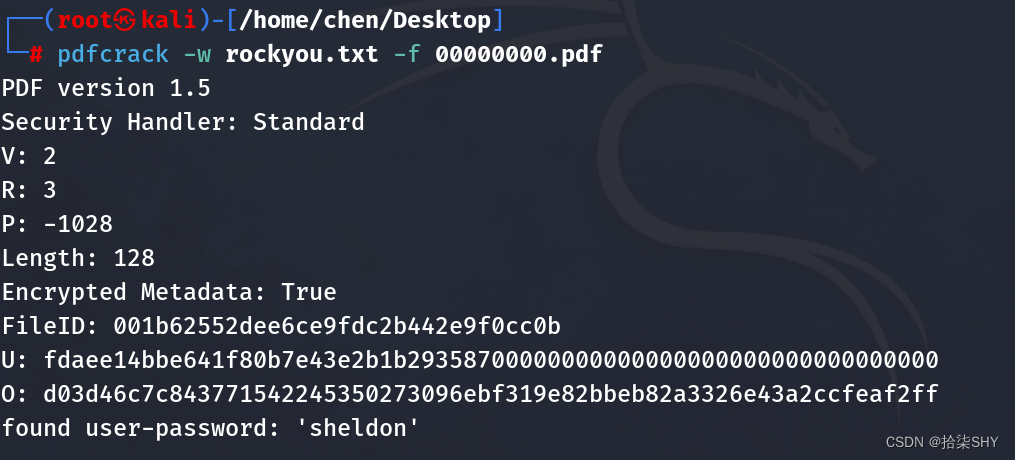
暴力破解pdf文档密码
首先安装pdfcrack工具包 apt install pdfcrack 默认密码字典存储在/usr/share/wordlists里,是gz文件,将它解压并copy到pdf目录 然后使用pdfcrack破解 密码在最后一行user-password的单引号里...

蓝桥杯刷题第四天
思路: 这道题很容易即可发现就是简单的暴力即可完成题目,我们只需满足所有数的和为偶数即可保证有满足条件的分法,同时也不需要存下每个输入的数据,只需要知道他是偶数还是奇数即可,因为我们只需要偶数个奇数搭配在一块…...

03-数据库的用户管理
一、创建新用户 mysql> create user xjzw10.0.0.% identified by 1; Query OK, 0 rows affected (0.01 sec) 二、查看当前数据库正在登录的用户 mysql> select user(); ---------------- | user() | ---------------- | rootlocalhost | ---------------- 1 row …...

每日一题 --- 三数之和[力扣][Go]
三数之和 题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意&#x…...
)
vue render 函数详解 (配参数详解)
vue render 函数详解 (配参数详解) 在 Vue 3 中,render 函数被用来代替 Vue 2 中的模板语法。 它接收一个 h 函数(或者是 createElement 函数的别名),并且返回一个虚拟 DOM。 render 函数的语法结构如下: render(h) …...
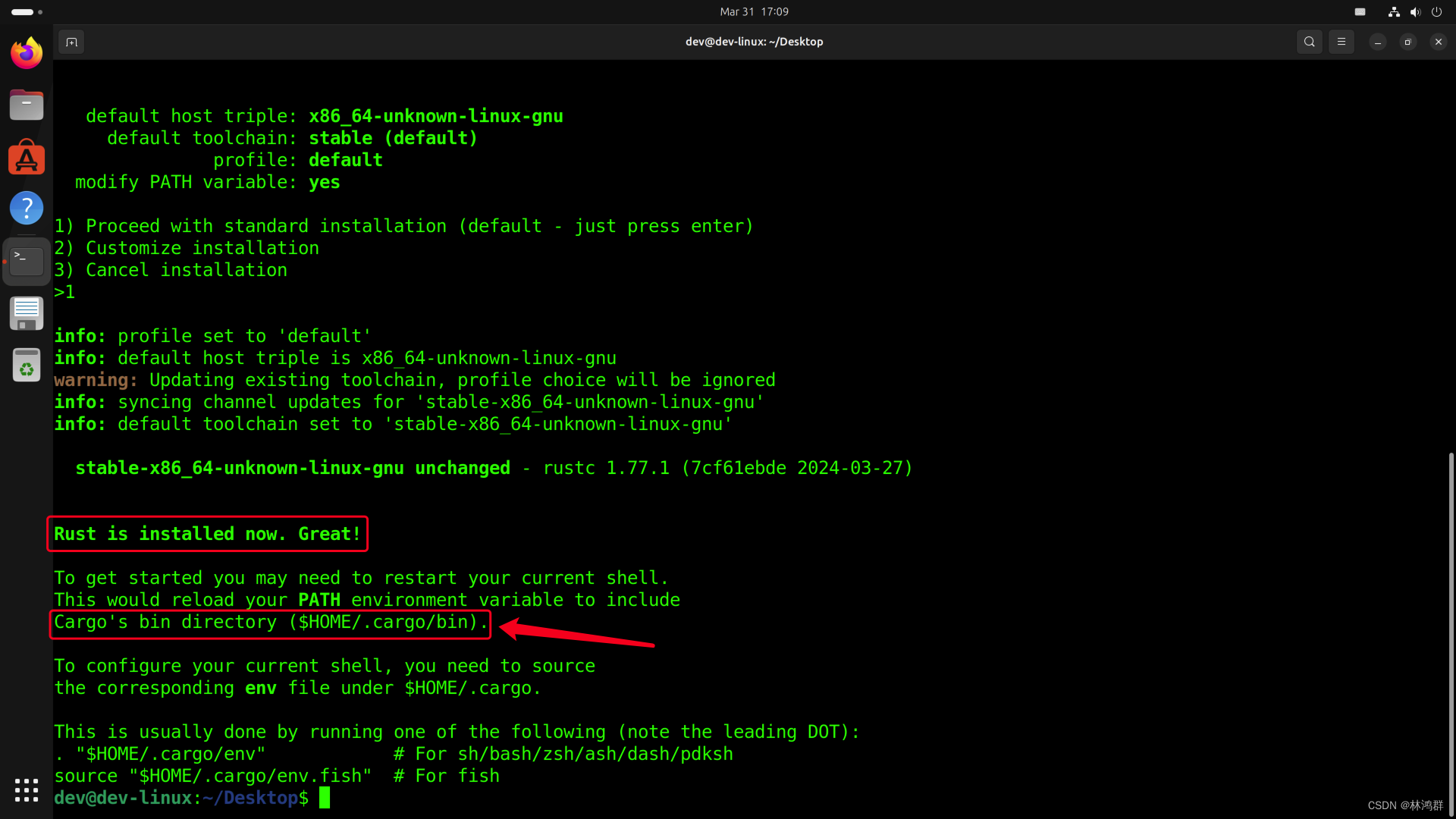
ubuntu23.10配置RUST开发环境
系统版本: gcc版本 下载rustup安装脚本: curl --proto =https --tlsv1.2 https://sh.rustup.rs -sSf | sh下载完成后会自动执行 选择默认安装选项 添加cargo安装目录到环境变量 vim ~/.bashrc<...

Vue性能优化--gZip
一、gZip简单介绍 1.1 什么是gzip gzip是GNUzip的缩写,最早用于UNIX系统的文件压缩。HTTP协议上的gzip编码是一种用来改进web应用程序性能的技术,web服务器和客户端(浏览器)必须共同支持gzip。目前主流的浏览器,Chro…...

蓝桥杯第七届大学B组详解
目录 1.煤球数量; 2.生日蜡烛; 3.凑算式 4.方格填数 5.四平方和 6.交换瓶子 7.最大比例 1.煤球数量 题目解析:可以根据题目的意思,找到规律。 1 *- 1个 2 *** 3个 3 ****** 6个 4 ********** 10个 不难发现 第…...

荣誉 | 人大金仓连续三年入选“金融信创优秀解决方案”
3月28日,由中国人民银行领导,中国金融电子化集团有限公司牵头组建的金融信创生态实验室发布“第三期金融信创优秀解决方案”,人大金仓新一代手机银行系统解决方案成功入选,这也是人大金仓金融行业解决方案连续第三年获得用户认可。…...
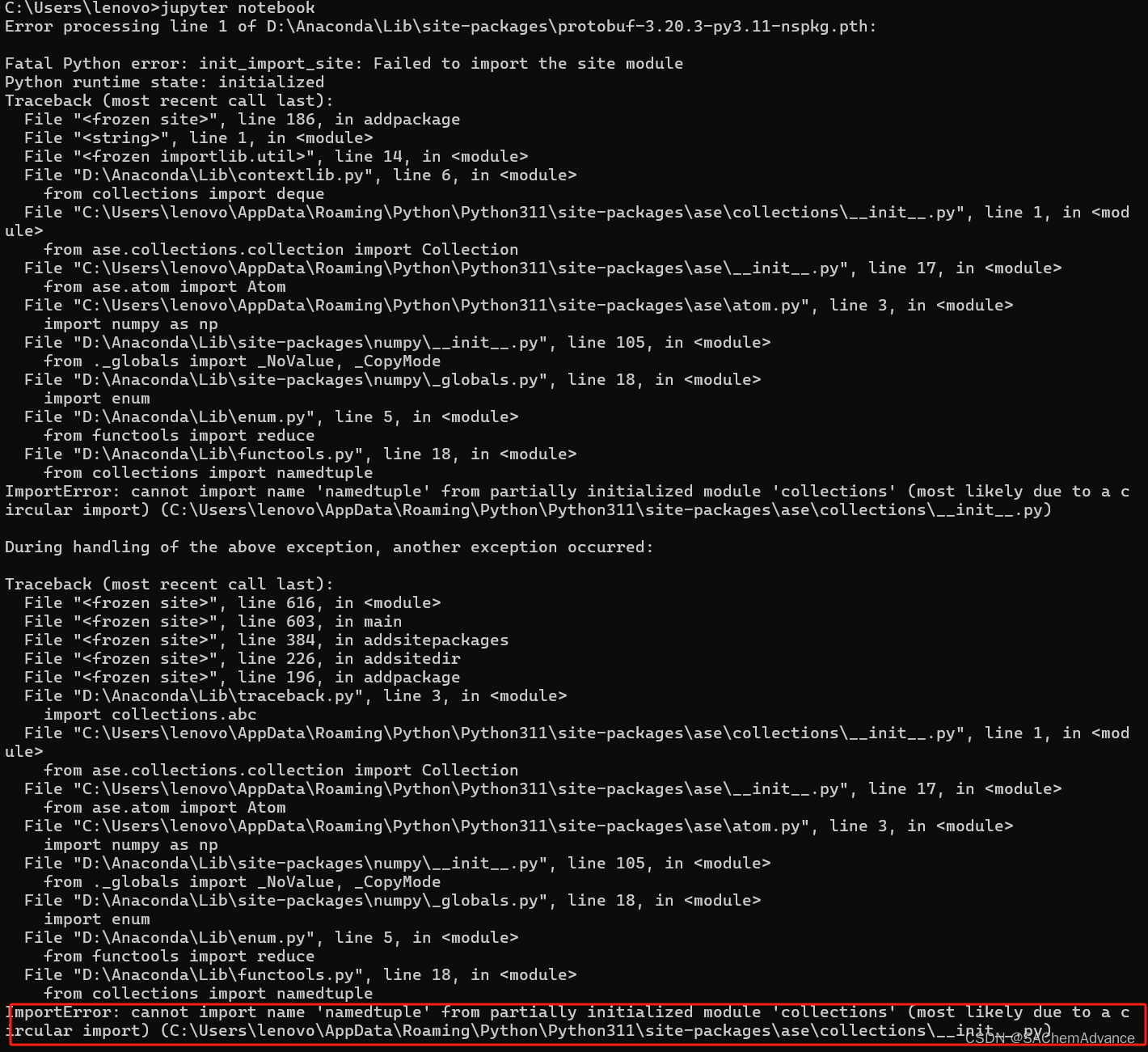
【关于jupyter notebook】一打开就闪退的问题
在Anaconda Prompt中输入jupyter notebook发现是有个错误。 里面多了一个__init__.py的文件导致报错。删除之后,就可以使用了...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
