春招冲刺百题计划--矩阵篇

289. 生命游戏
题目:
给定一个包含
m × n个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态:1即为 活细胞 (live),或0即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你
m x n网格面板board的当前状态,返回下一个状态。
思考:
方法一:暴力破解
这个问题看起来很简单,但有一个陷阱,如果你直接根据规则更新原始数组,那么就做不到题目中说的 同步 更新。假设你直接将更新后的细胞状态填入原始数组,那么当前轮次其他细胞状态的更新就会引用到当前轮已更新细胞的状态,但实际上每一轮更新需要依赖上一轮细胞的状态,是不能用这一轮的细胞状态来更新的。
所以我们需要创建一个同样大小的数组,用来存储变化后的值。
创建数组代码如下:
vector<vector<int>> nextBoard(m, vector<int>(n, 0)); // 创建一个新的矩阵来存储下一步的状态接下来,我们需要计算周围8个格加起来的活细胞数量。但这里要注意边界情况。
8个格子(普通版),边界需要处理,if语句,写起来又臭又长。
ans+= matirex[i-1][j]+matirex[i+1][j]+matirex[i][j-1]+matirex[i][j+1]+matirex[i-1][j-1]+matirex[i+1][j+1]+matirex[i+1][j-1]+matirex[i-1][j+1];所以不妨设置移动变量 dx,dy.先将x,y进行变化,然后判断越界情况。
for (int dx = -1; dx <= 1; dx++) {for (int dy = -1; dy <= 1; dy++) {if (dx == 0 && dy == 0) continue; // 跳过当前位置int x = i + dx;int y = j + dy;if (x >= 0 && x < m && y >= 0 && y < n) {//在区域内count += matrix[x][y];}}}
再根据生存规律判断细胞实际存活情况 。
最后将结果复制回数组中。
class Solution {
public:int num(vector<vector<int>>& matrix, int i, int j) {int count = 0;int m = matrix.size();int n = matrix[0].size();for (int dx = -1; dx <= 1; dx++) {for (int dy = -1; dy <= 1; dy++) {if (dx == 0 && dy == 0) continue; // 跳过当前位置int x = i + dx;int y = j + dy;if (x >= 0 && x < m && y >= 0 && y < n) {count += matrix[x][y];}}}return count;}void gameOfLife(vector<vector<int>>& board) {int m = board.size();int n = board[0].size();vector<vector<int>> nextBoard(m, vector<int>(n, 0)); for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int liveNeighbors = num(board, i, j);// 根据规则更新下一步的状态if (board[i][j] == 1 && (liveNeighbors == 2 || liveNeighbors == 3)) {nextBoard[i][j] = 1; // 存活状态} else if (board[i][j] == 0 && liveNeighbors == 3) {nextBoard[i][j] = 1; // 重生} else {nextBoard[i][j] = 0; // 死亡}}}// 将下一步状态复制回原矩阵for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {board[i][j] = nextBoard[i][j];}}}
};
复杂度:时间复杂度0(mn),空间复杂度0(mn)。
方法二:使用额外的状态
方法一中O(mn) 的空间复杂度在数组很大的时候内存消耗是非常昂贵的。题目中每个细胞只有两种状态 live(1) 或 dead(0),但我们可以拓展一些复合状态使其包含之前的状态。举个例子,如果细胞之前的状态是 0,但是在更新之后变成了 1,我们就可以给它定义一个复合状态 2。这样我们看到 2,既能知道目前这个细胞是活的,还能知道它之前是死的。
根据生存规律判断细胞实际存活情况,规则修正如下:
规则 1:如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡。这时候,将细胞值改为 -1,代表这个细胞过去是活的现在死了;
规则 2:如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活。这时候不改变细胞的值,仍为 1;
规则 3:如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡。这时候,将细胞的值改为 -1,代表这个细胞过去是活的现在死了。可以看到,因为规则 1 和规则 3 下细胞的起始终止状态是一致的,因此它们的复合状态也一致;
规则 4:如果死细胞周围正好有三个活细胞,则该位置死细胞复活。这时候,将细胞的值改为 2,代表这个细胞过去是死的现在活了。
另外:计数方式也需要改一下,只有当abs(board[x][y]) == 1时,原先才是活的,进行计数
// 根据规则更新下一步的状态if (board[i][j] == 1 && (liveNeighbors < 2 || liveNeighbors > 3)) {board[i][j] = -1; // 存活状态} else if (board[i][j] == 0 && liveNeighbors == 3) {board[i][j] = 2; // 重生} //其他位置保持不变即可//计数方式:if (x >= 0 && x < m && y >= 0 && y < n&&(abs(board[x][y]) == 1)) {count += 1;}最后再讲2更改为 1;3更改为0 即可。
代码如下:
class Solution {
public:int num(vector<vector<int>>& matrix, int i, int j) {int count = 0;int m = matrix.size();int n = matrix[0].size();for (int dx = -1; dx <= 1; dx++) {for (int dy = -1; dy <= 1; dy++) {if (dx == 0 && dy == 0) continue; // 跳过当前位置int x = i + dx;int y = j + dy;if (x >= 0 && x < m && y >= 0 && y < n&&(abs(matrix[x][y]) == 1)) {count += 1;}}}return count;}void gameOfLife(vector<vector<int>>& board) {int m = board.size();int n = board[0].size();//vector<vector<int>> nextBoard(m, vector<int>(n, 0)); // 创建一个新的矩阵来存储下一步的状态for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int liveNeighbors = num(board, i, j);// 根据规则更新下一步的状态if (board[i][j] == 1 && (liveNeighbors < 2 || liveNeighbors > 3)) {board[i][j] = -1; // 存活状态} else if (board[i][j] == 0 && liveNeighbors == 3) {board[i][j] = 2; // 重生} //其他位置保持不变即可}}// 将下一步状态复制回原矩阵for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if(board[i][j]>0) board[i][j] = 1;else board[i][j] = 0;}}}
};

48. 旋转图像
题目:
给定一个 n × n 的二维矩阵
matrix表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
思路:要求原地修改数组,说明空间复杂度需要为0(1),考虑使用swap,调换数组位置。
常用调换位置方法:
1.中心反转
swap(matrix[i][j],matrix[j][i]);
swap(matrix[i][j],matrix[n-j-1][n-i-]);
2.水平翻转 swap(matrix[i][j],matrix[n-i-1][j]);
3.数列翻转 swap(matrix[i][j],matrix[i][n-j-1]);
翻转问题一定注意下标的范围,反转只需要换一半!!!
例如水平和数列 n/2,中心就是j<i
本题研究一下发现只需要中心翻转+数列翻转一下即可
matrix =[[1,2,3],[4,5,6],[7,8,9]]
中心翻转后:[[1,4,7],[2,5,8],[3,6,9]] swap(matrix[i][j],matrix[j][i]);
数列翻转:[[7,4,1],[8,5,2],[9,6,3]]
代码:
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int n=matrix.size();for(int i=0;i<n;i++){for(int j=0;j<i;j++){swap(matrix[i][j],matrix[j][i]);}}for(int i=0;i<n;i++){for(int j=0;j<n/2;j++){swap(matrix[i][j],matrix[i][n-j-1]);}}}
};73. 矩阵置零
题目:
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
方法一:开一个二维数组
1.一个直观的解决方案是使用 O(mn) 的额外空间,但这并不是一个好的解决方案。
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<vector<int>> res(m, vector<int>(n, 1));for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {for (int k = 0; k < n; k++)res[i][k] = 0;for (int k = 0; k < m; k++)res[k][j] = 0;}}}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {matrix[i][j] = matrix[i][j] * res[i][j];}}}
};方法二:创建两个额外的数组来记录哪些行和列需要被置零
一个简单的改进方案是使用 O(m + n) 的额外空间,但这仍然不是最好的解决方案
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();vector<int> res_row(m, 1);vector<int> res_col(n, 1);for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {res_row[i]=0;res_col[j]=0;}}}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {matrix[i][j] = matrix[i][j] * res_row[i]*res_col[j];}}}
};方法三:使用两个标记变量
我们可以用矩阵的第一行和第一列代替方法一中的两个标记数组,以达到 O(1) 的额外空间。但这样会导致原数组的第一行和第一列被修改,无法记录它们是否原本包含 0。因此我们需要额外使用两个标记变量分别记录第一行和第一列是否原本包含 0。
在实际代码中,我们首先预处理出两个标记变量,接着使用其他行与列去处理第一行与第一列,然后反过来使用第一行与第一列去更新其他行与列,最后使用两个标记变量更新第一行与第一列即可。
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int m = matrix.size();int n = matrix[0].size();int flag_col0 = false, flag_row0 = false;for (int i = 0; i < m; i++) {if (!matrix[i][0]) {flag_col0 = true;}}for (int j = 0; j < n; j++) {if (!matrix[0][j]) {flag_row0 = true;}}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (!matrix[i][j]) {matrix[i][0] = matrix[0][j] = 0;}}}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (!matrix[i][0] || !matrix[0][j]) {matrix[i][j] = 0;}}}if (flag_col0) {for (int i = 0; i < m; i++) {matrix[i][0] = 0;}}if (flag_row0) {for (int j = 0; j < n; j++) {matrix[0][j] = 0;}}}
};


相关文章:

春招冲刺百题计划--矩阵篇
289. 生命游戏 题目: 给定一个包含 m n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与…...
LLM大语言模型(八):ChatGLM3-6B使用的tokenizer模型BAAI/bge-large-zh-v1.5
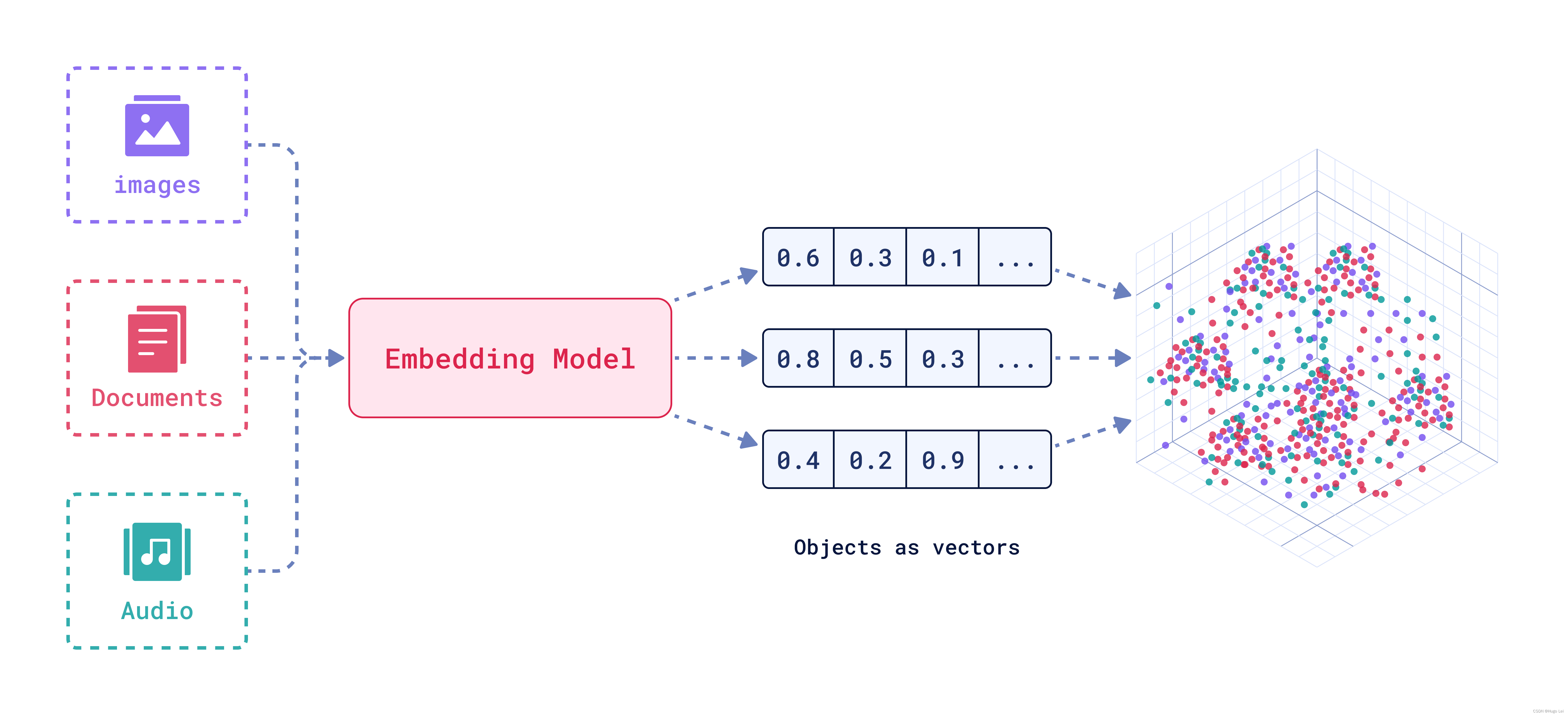
背景 BGE embedding系列模型是由智源研究院研发的中文版文本表示模型。 可将任意文本映射为低维稠密向量,以用于检索、分类、聚类或语义匹配等任务,并可支持为大模型调用外部知识。 BAAI/BGE embedding系列模型 模型列表 ModelLanguageDescriptionq…...

MySQL中的三种日志
MySQL 包括三种类型的⽇志,分别是 binlog、 redolog 和 undolog,它们分别有不同的作⽤和特点。 binlog (存档日志) binlog(Binary log)是 MySQL 中的⼆进制⽇志⽂件,是 Server 层⽣成的的⽇志…...
(A,B,C,D))
Codeforces Round 932 (Div. 2)(A,B,C,D)
比赛链接 AB都是思维,更确切地说,A考了字符串字典序,很经典的贪心考点,B考了MEX运算。C出的还是比较好的,dp方法值得学习。D题是个不太好想的容斥,主要是变量有点多,容易搞混。 A. Entertainme…...
初识C++ · 入门(2)
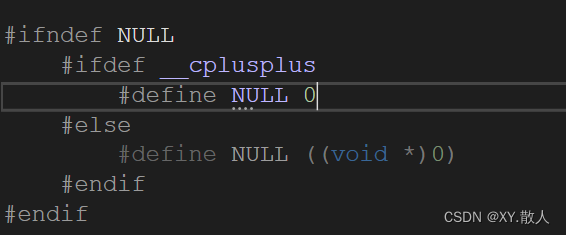
目录 1 引用 1.1引用的概念 1.2 引用的特性 2 传值,传引用的效率 3 引用和指针的区别 4 内联函数 4.1 内联函数的定义 4. 2 内联函数的特性 5 关键字auto 5.1关于命名的思考 5.2 关于auto的发展 5.3 auto使用规则 6 范围for的使用 7 空指针 1 引用 …...
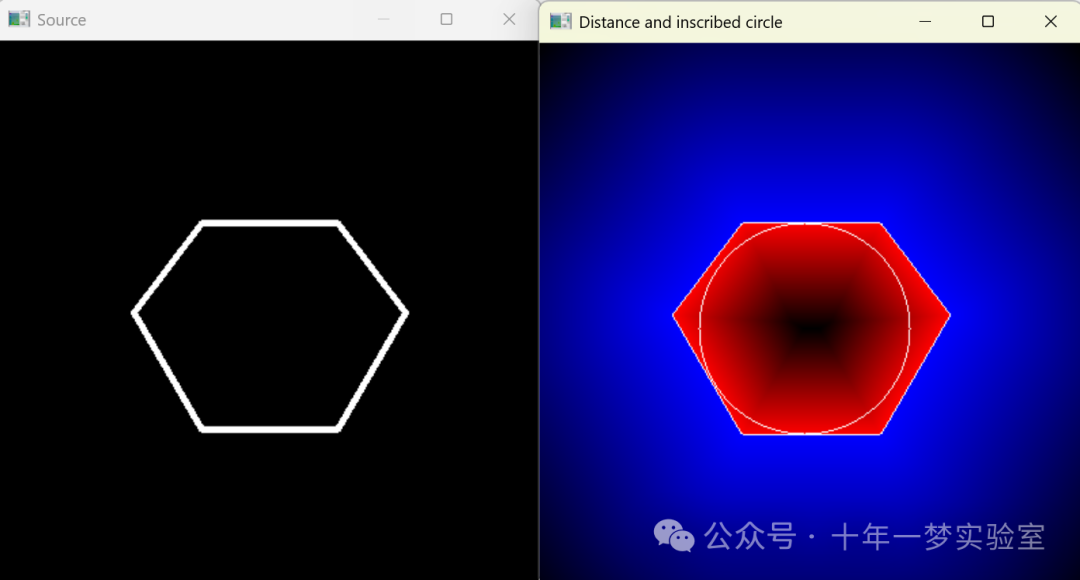
【opencv】教程代码 —ShapeDescriptors
检测和显示图像的轮廓 在图像中搜索并显示轮廓边缘多边形、轮廓矩形和包围圆 获取包含检测到的轮廓的椭圆和旋转的矩形 图像轮廓检测和轮廓凸包 计算图像中的轮廓的矩(包括面积、重心等)并进行显示 创建和绘制一个多边形图像然后计算并显示图像上每个点到…...

2024-03-28 Java8之Collectors类
Collectors类常用方法 文章目录 Collectors类常用方法1.toList、toSet、toMap2.joining、counting、summingInt、minBy3.groupingBy 1.toList、toSet、toMap Collector<T, ?, List<T>> toList(); //收集为List集合 Collector<T, ?, Set<T>> toSet()…...
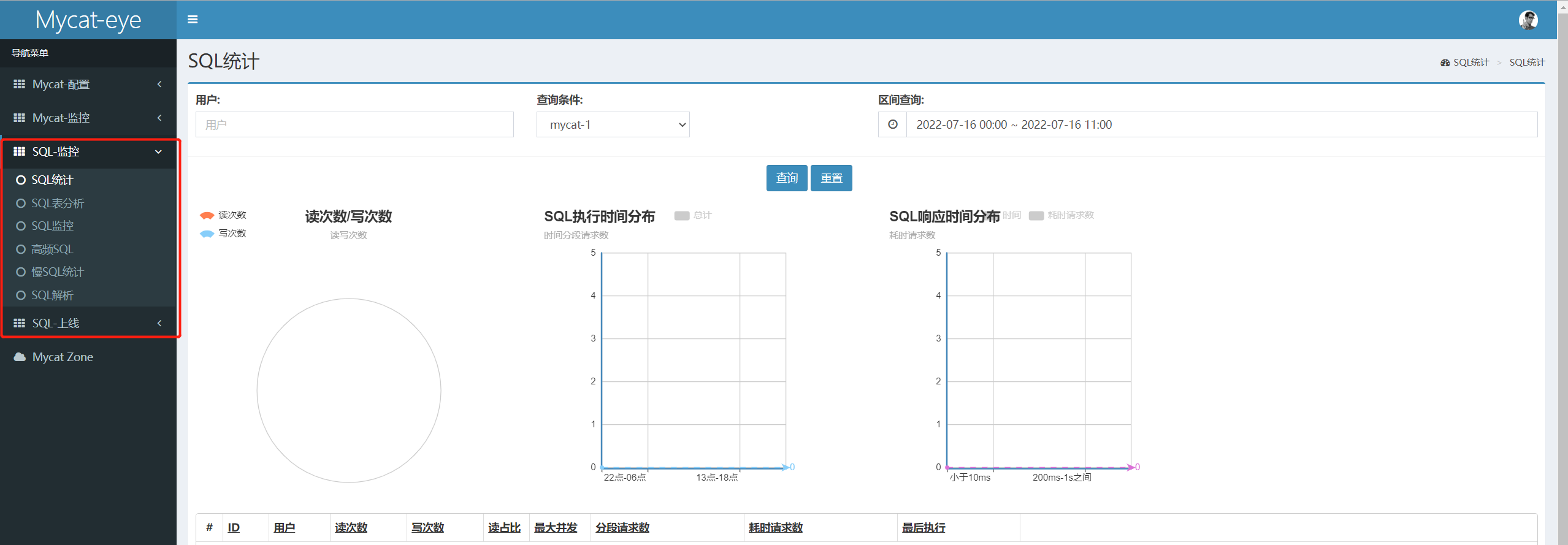
第116讲:使用Mycat-eye管理Mycat数据库服务
文章目录 1.Mycat的管理工具2.Mycat-eye介绍3.部署Mycat-eye3.1.安装Zookeep3.2.安装Mycat-eye3.3.访问Mycat-eye 4.在Mycat-eye中导入Mycat服务的信息 1.Mycat的管理工具 Mycat默认开通2个端口,可以在server.xml中进行修改。 8066 数据访问端口,即进行…...

XR虚拟直播间,引领创新风潮,打破直播局限!
随着互联网技术日新月异的发展,直播行业也迎来了蓬勃发展的春天。然而,大多数直播间在吸引观众眼球和延长用户观看时长方面,仍然面临着巨大的挑战。正是在这样的背景下,XR虚拟直播系统应运而生,以其多维度的直播场景、…...
unity双层滑动实现
实现功能: 当滑动列表中内容处于顶端的时候,向上滑动优先滑动整个滑动列表,当滑动列表移动到设置位置,即设定的最高处时,继续移动列表内内容。向下移动亦然,当内容处于滑动列表顶端时,移动整个滑…...

浅谈AI技术创业有哪些机会?
一、AI技术创业概念简介 AI技术创业指的是利用人工智能(Artificial Intelligence,AI)技术进行创业活动。人工智能是指计算机系统能够模拟和展现出人类智能的一种技术。在AI技术创业中,创业者利用AI技术来解决现实生活中的问题&…...
大数据-TXT文本重复行计数工具
支持系统类型:Windows 64位系统 Linux 64位系统 苹果64位系统 硬盘要求:固态硬盘(有效剩余磁盘空间大小最低3倍于大数据文件的大小) 内存要求:最低8G(例如只有几百G数据) 如果处理TB级大数据文…...

【无标题】331
2024年3月31日19:26:09 和一个好感度为40的女生完成了一次基础的对话 2024年3月31日19:26:26 在群里完成了一个毫无所谓的对话 2024年3月31日19:40:04开始准备写论文了 2024年3月31日19:40:11好感度为40的女生回复了我本质上是回复率只有40的人回复了我那应该感到高兴才对 …...
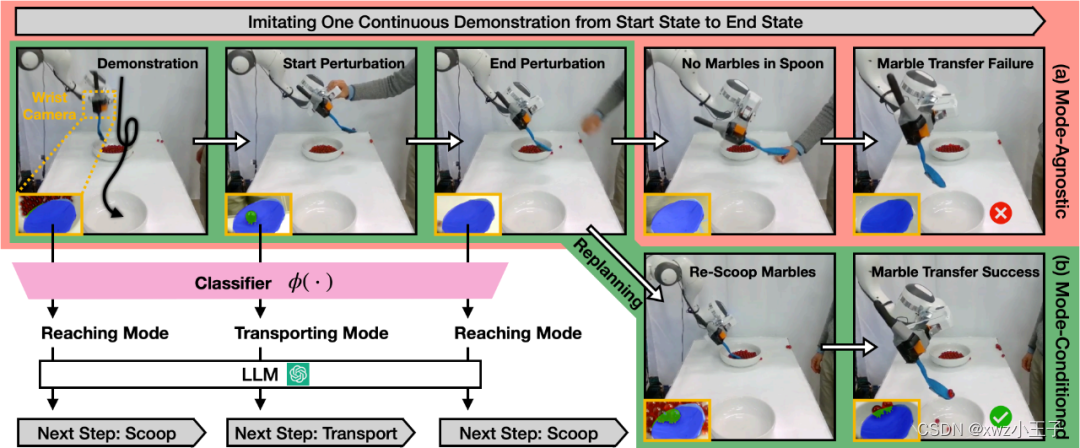
MIT最新研究成果 机器人能够从错误中纠偏 无需编程介入和重复演示
目前科学家们正在努力让机器人变得更加智能,教会他们完成诸如擦拭桌面,端盘子等复杂技能。以往机器人要在非结构化环境执行这样的任务,需要依靠固定编程进行,缺乏场景通用性,而现在机器人的学习过程主要在于模仿&#…...

C语言—指针数组
从键盘任意输入一个整型表示的月份值,用指针数组编程输出该月份的英文表示,若输入的月份值不在1~12之间,则输出“Illegal month”。 **输入格式要求:"%d" 提示信息:"Input month number:&q…...

OpenCV图像二值化
1.二值图像 灰度图像 0 - 255二值图像 0(黑) / 255(白) 2.二值分割 五种阈值分割方法(阈值T): 大于T为255,小于T为0 大于T为0,小于T为255 小于T为原值 else T 小于…...

java中的抽象类
抽象类是指包含了抽象方法的类。在java中,抽象方法指的是用abstract关键字进行修饰的方法,抽象方法与普通的方法的最大区别就是抽象方法没有方法体,也就是说抽象方法是没有具体的实现的。这也就意味着在抽象类的子类中调用抽象方法时…...

代码随想录算法训练营第二十天| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
系列文章目录 目录 系列文章目录654.最大二叉树递归法[左闭右开)[左闭右闭] 617.合并二叉树递归法(前中后序都可,以前序为例)迭代法(类似 101. 对称二叉树 写法,可用双端队列/单端队列<栈>,以单端队列…...

2014年认证杯SPSSPRO杯数学建模A题(第二阶段)轮胎的花纹全过程文档及程序
2014年认证杯SPSSPRO杯数学建模 A题 轮胎的花纹 原题再现: 轮胎被广泛使用在多种陆地交通工具上。根据性能的需要,轮胎表面常会加工出不同形状的花纹。在设计轮胎时,往往要针对其使用环境,设计出相应的花纹形状。 第二阶段问…...
C#全新一代医院手术麻醉系统围术期全流程源码
目录 一、麻醉学科的起源 二、麻醉前访视与评估记录单 患者基本信息 临床诊断 患者重要器官功能及疾病情况 病人体格情况分级 手术麻醉风险评估 拟施麻醉方法及辅助措施 其他需要说明的情况 访视麻醉医师签名 访视时间 与麻醉相关的检查结果 三、手术麻醉信息系统…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
