算法沉淀 —— 深度搜索(dfs)
算法沉淀 —— 深度搜索(dfs)
- 一、计算布尔二叉树的值
- 二、求根节点到叶节点数字之和
- 三、二叉树剪枝
- 四、验证二叉搜索树
- 五、二叉搜索树中第K小的元素
一、计算布尔二叉树的值
【题目链接】:2331. 计算布尔二叉树的值
【题目】:

【分析】:
在确定一颗二叉树的布尔值前,我们需要先得到左子树、右子树的结果(0/1)。如果左子树、右子树不是叶子节点,显然这是一个递归子问题(将求左子树、右子树的布尔值);
最后就是根据root的值来判断对左/右子树结果的操作(如果是2,按位或;否则为按位与)
【代码实现】:
class Solution {
public:bool evaluateTree(TreeNode* root) {if(root->left == nullptr && root->right == nullptr)return root->val;//完成二叉树保证如果非叶子节点,则左右子树都不为空bool ansL = evaluateTree(root->left);//递归处理左子树bool ansR = evaluateTree(root->right);//递归处理右子树return root->val == 2 ? ansL | ansR : ansL & ansR;}
};
二、求根节点到叶节点数字之和
【题目链接】:129. 求根节点到叶节点数字之和
【题目】:

【分析】:
根节点到叶节点数字之和,显然如果当前节点为叶子节点,此时直接返回结果;否则需要得到当前路径之前路径和(假设为prev),此时当前路径数字和为root->val + prev*10。此时在重复上述过程,如果时叶子节点,直接返回结果;否则转化为递归子问题求解(左子树、右子树只有非空,都有结果)
由于根节点到叶节点的路径可能存在多条,每一条路径都存在一个结果。所以这里我们可以定义一个全局变量来记录最后的累计结果。(具体看代码)
【代码实现】:
class Solution {
public:int sum = 0;int sumNumbers(TreeNode* root) {int prev = 0;_sumNumbers(root, 0);//prev用于记录当前节点前的路径和return sum;}void _sumNumbers(TreeNode* root, int prev){prev = prev * 10 + root->val;//还是使用prev来保存当前路径数字和if(root->left)//左子树非空,必然存在结果,转化成递归子问题求解_sumNumbers(root->left, prev);if(root->right)//右子树非空,同上_sumNumbers(root->right, prev);if(root->left == nullptr && root->right == nullptr)//叶子节点, 累加当前路径和sum += prev;}
};
三、二叉树剪枝
【题目链接】:814. 二叉树剪枝
【题目】:

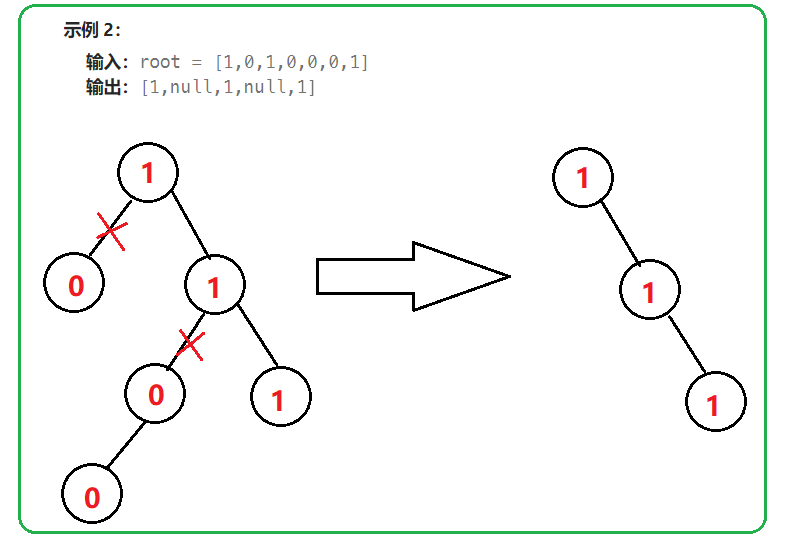
【分析】:
本题中,我们可以采用二叉树后序遍历的思想。先对左子树、右子树分别进行剪枝操作。此时左/右子树中有两种结果:非空、非空(此时子树已经进行了剪枝)。所以此时当前节点必须满足左/右子树均为空,并且根节点为0时,才可继续剪枝。
【代码实现】:
class Solution {
public:TreeNode* pruneTree(TreeNode* root) {//二叉树后序遍历,进行剪枝//对左/右子树剪枝后,左/右子树只有两种结果: 为空、剪完枝非空。if(root == nullptr)return nullptr;root->left = pruneTree(root->left);//对左子树剪枝root->right = pruneTree(root->right);//右子树剪枝if(root->left == nullptr && root->right == nullptr && root->val == 0){delete root;//笔试建议省略此步,原因在于如果root不是new出来的,会报错root = nullptr;}return root;}
};
四、验证二叉搜索树
【题目链接】:98. 验证二叉搜索树
【题目】:

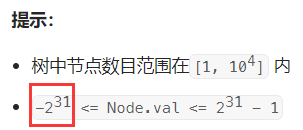
【分析】:
我们可以利用二叉搜索树中序遍历是升序的性质来判断是否为二叉搜索树。但如何利用呢?
其中一种思路是先用一个数组记录二叉树中序遍历结果,在判断是否为升序。但此时算法的空间复杂度为O(n)。
另一种思路就是使用一个全局遍历(prev)来记录中序遍历的前一个数据,然后转化成当前节点和prev比较(当然还有prev值更新啦)。让后根据左子树、右子树、根节点的结果来判断是否符合AVL树(具体参考代码)
tips:
- prev的初始值需要设置为LLONG_MIN(比INT_MIN小即可)。
【代码实现】:
class Solution {
public:long long prev = LLONG_MIN;//保存中序遍历的前一个节点值bool isValidBST(TreeNode* root) {if(root == nullptr)return true;bool Left = isValidBST(root->left);//记录左子树结果bool cur = false;//记录当前根节点和上一个数据是否符合AVL树性质if(root->val > prev){prev = root->val;cur = true;}bool Right = isValidBST(root->right);//记录左子树结果return Left && Right && cur;}
};
五、二叉搜索树中第K小的元素
【题目链接】:230. 二叉搜索树中第K小的元素
【题目】:

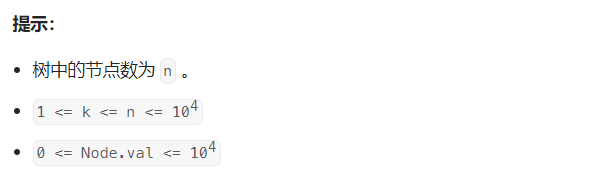
【分析】:
本题意思非常明确,求第k小元素。我们可以通过中序遍历,每遍历一次元素,k–。直到k为1时,返回结果。
这里博主推荐将返回值(定义为ret)、和k的值都设置为全局变量。然后和中序遍历一样,我们只需当k的值为1时,返回结果结果;并且每次遍历k–。
【代码实现】:
class Solution {
public:int count = 0, ret = 0;int kthSmallest(TreeNode* root, int k) {count = k;_kthSmallest(root);return ret;}void _kthSmallest(TreeNode* root){if(root == nullptr || count == 0)return;_kthSmallest(root->left);if(--count == 0)ret = root->val;_kthSmallest(root->right);}
};
相关文章:

算法沉淀 —— 深度搜索(dfs)
算法沉淀 —— 深度搜索(dfs) 一、计算布尔二叉树的值二、求根节点到叶节点数字之和三、二叉树剪枝四、验证二叉搜索树五、二叉搜索树中第K小的元素 一、计算布尔二叉树的值 【题目链接】:2331. 计算布尔二叉树的值 【题目】: …...
)
#设计模式#3.1用做松鼠桂鱼来理解抽象工厂(对象创建型模式)
概念:xx工厂,xx产品 区分 工厂是动作,产品是结果(菜品) 概念:抽象xx,具体xx 区分 抽象产品:“中式菜品” 具体产品:“麻婆豆腐”、“宫保鸡丁” 抽象工厂:“…...

adb基本命令
下载安装 adb 概述: ADB 全称为 Android Debug Bridge,起到调试桥的作用,是一个客户端-服务器端程序。其中客户端是用来操作的电脑,服务端是 Android 设备。 下载地址: Windows版本:https://dl.google.com/android/repository/pl…...

小工具实战-Python实现小工具输出字符串大小写转换、字符串统计、编解码、MD5加密
小工具实战-Python实现小工具输出字符串大小写转换、字符串统计、编解码、MD5加密 学习建议字符串大小写转换实现思路部分代码 字符串统计实现思路部分代码: 字符串编解码实现思路部分代码 字符串MD5加密实现思路部分代码 小工具整体设计设计思路工具完整代码实现输…...

MySQL进阶-----索引的语法与SQL性能分析
目录 前言 一、索引语法 1.SQL语法 2.案例演示 二、SQL性能分析 三、慢查询日志 1.开启日志 2.测试样例 四、profile详情 1.开启profile 2.profile测试SQL语句 五、explain详情 1.语法结构 2.执行顺序示例(id) 3.执行性能示例(type) 前言 本…...

Ansible剧本playbooks详解
一、playbook简介 playbook是ansible用于配置,部署和管理托管主机剧本,通过playbook的详细描述,执行其中一系列tasks,playbook字面意思是剧本,现实中由演员按剧本表演,在ansible中由计算机进行安装&#x…...
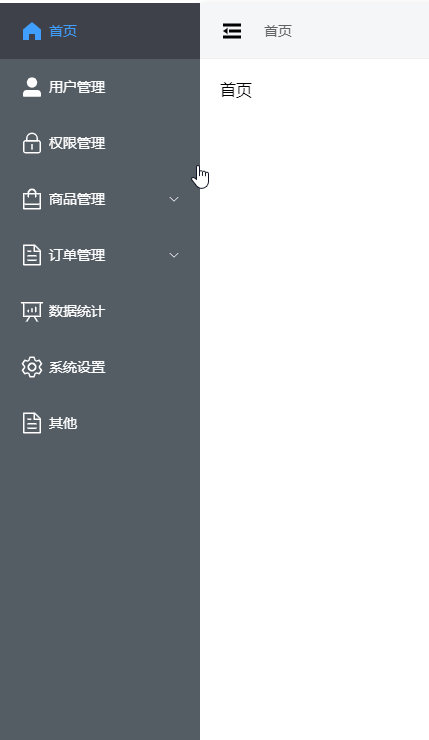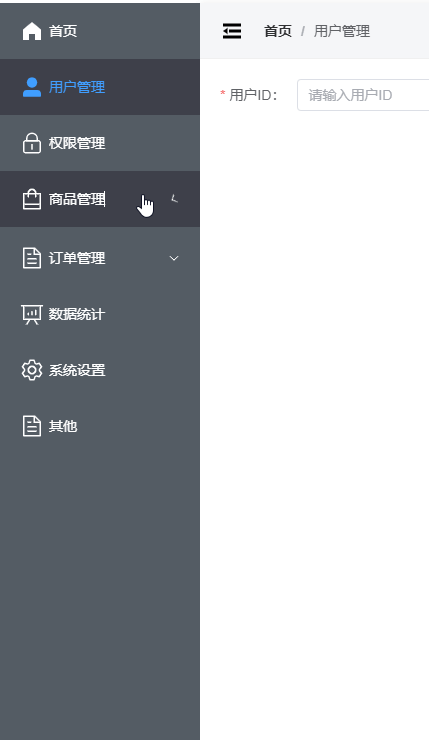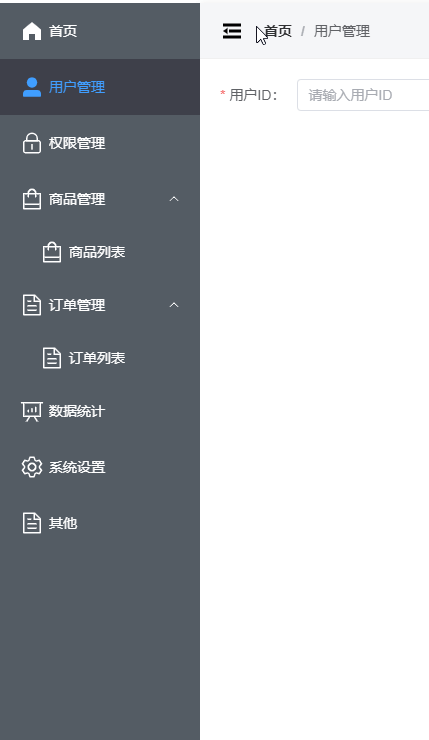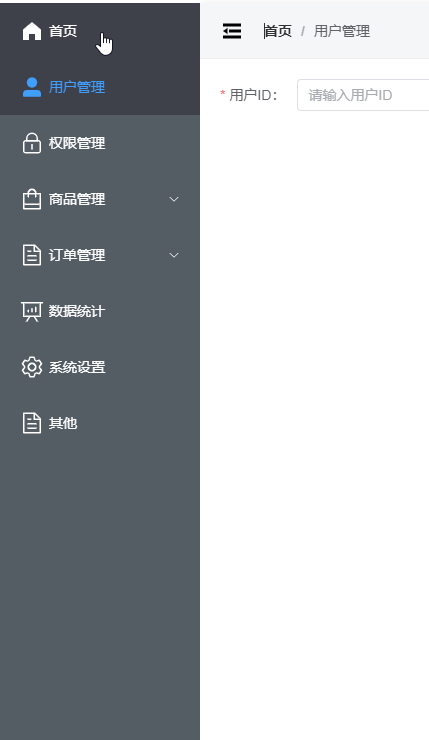
vue3封装Element导航菜单
1. 导航外层布局 AsideView.vue <template><el-menu:default-active"defaultActive"class"my-menu":collapse"isCollapse":collapse-transition"false"open"handleOpen"close"handleClose"><menu…...

字符串的函数
头文件 # include <string.h> 五大函数: strlen()、strcpy、strcat()、strcmp()、strstr() 用法: strlen():计算字符串长度,但不计\0这个字符 #include <string.h> int main() {char arr[] "abcdef"…...
Linux安装redis(基于CentOS系统,Ubuntu也可参考)
前言:本文内容为实操记录,仅供参考! 一、下载并解压Redis 1、执行下面的命令下载redis:wget https://download.redis.io/releases/redis-6.2.6.tar.gz 2、解压redis:tar xzf redis-6.2.6.tar.gz 3、移动redis目录&a…...

ChatGPT引领量化交易革命:AI在金融创新的浪潮中崭露头角
随着科技的飞速发展,金融领域正迎来一场前所未有的创新浪潮。在这场变革中,ChatGPT凭借其卓越的自然语言处理能力和深度学习能力,正引领量化交易进入新时代。 量化交易,作为现代金融领域的一种重要交易方式,依赖于复杂的数学模型和大量的历史数据来制定交易策略。然而,传…...
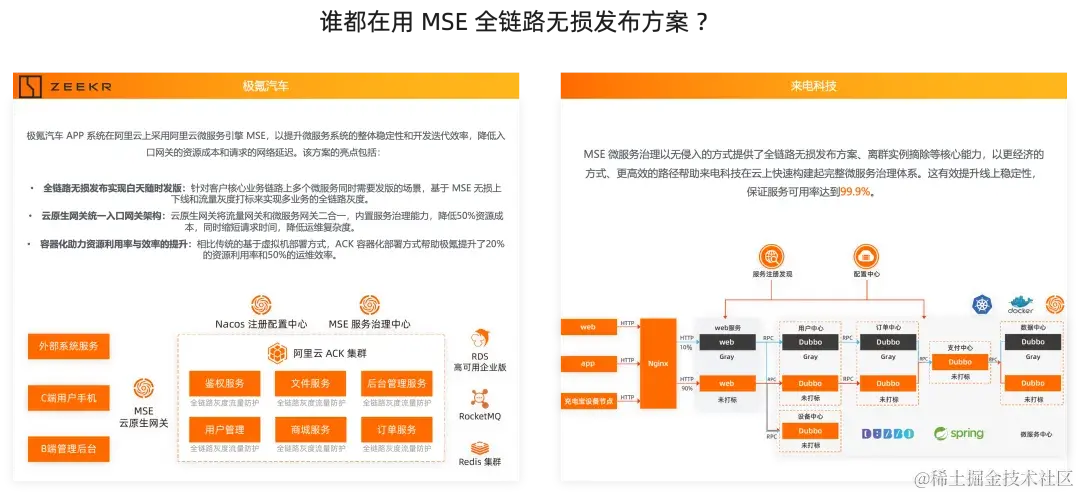
无忧微服务:如何实现大流量下新版本的发布自由
作者:项良、十眠 微服务上云门槛降低,用好微服务才是关键 据调研数据显示,约 70% 的生产故障是由变更引起的。在阿里云上的企业应用如茶百道、极氪汽车和来电等,他们是如何解决变更引起的稳定性风险,实现了在白天高流…...

Halcon3D表面平面度检测-平面差值法
//倾斜平面矫正 https://blog.csdn.net/m0_51559565/article/details/137146179 //平面度和平面缺陷检测,平面矫正法 https://blog.csdn.net/m0_51559565/article/details/137163729前言 通常我们对表面平面度进行检测时,通常使用2种方式。1:…...
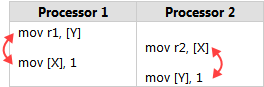
golang 在多线程中避免 CPU 指令重排
发布日期:2024-03-26 16:29:39 起因 golang 的发明初衷便是多线程,是一门专门用于多线程高并发的编程语言。其独创的 GMP 模型在多线程的开发上提供了很大的便利。 现代计算机基本上都是多核 CPU 的结构。CPU 在进行指令运行的时候,为了提高…...

自动化更新包文件--shell脚本
自动化更新包文件--shell脚本 背景手动更包自动化更包 背景 作为一名实施工程师,当然也协助做些测试的工作,当产品功能开发后,研发会将本次迭代涉及的前后端包文件提供过来。有时会因为一些原因研发没法现场开发,那就需要我们配合…...

Vue element-plus 导航栏 [el-menu]
导航栏 [el-menu] Menu 菜单 | Element Plus el-menu有很多属性和子标签,为网站提供导航功能的菜单。 常用标签: 它里面有两个子标签。el-menu-item,它其实就是el-menu每一个里面的item,item就是真实匹配到路由的每个栏目&#…...

数据结构——数组
数组定义: 在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识。 因为数组内的元素是连续存储的,所以数组中元素的地址,可以通过其索引计算出来。 性…...

python asyncio websockets server
python websocket server在收到接受消息处理完后会默认关闭连接。需要在msg_handler里面加个while true就能一直保持连接了。 start_server websockets.serve(msg_handler, "0.0.0.0", 29967) asyncio.get_event_loop().run_until_complete(start_server) asyncio.…...
视频素材免费网站有哪些?8个视频素材库网站下载推荐
在视频创作领域,选择正确的高质量无水印素材网站能够极大地丰富您的作品,让每一帧都鲜活起来。下面,我们继续为您介绍更多优质的视频素材网站,每一个都是您创作旅程中的宝贵资源。 1. 蛙学府(中国) 集合了…...
ChatGPT与传统搜索引擎的区别:智能对话与关键词匹配的差异
引言 随着互联网的快速发展,信息的获取变得比以往任何时候都更加便捷。在数字化时代,人们对于获取准确、及时信息的需求愈发迫切。传统搜索引擎通过关键词匹配的方式为用户提供了大量的信息,然而,这种机械式的检索方式有时候并不…...
)
xargs后调用bash自定义函数(写该函数文本到脚本, 并引导PATH)
xargs后调用bash自定义函数 需要3步骤,如下 function to_markdown_href_func() { fp$1 #echo $fpecho -e "\n[${fp}](${PREFIX}/${fp})" }BIN/tmp/bin/ F$BIN/to_markdown_href_func.sh mkdir -p $BIN 获得函数to_markdown_href_func的文本 ,写文本到 /tmp/bin/to_ma…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...
