【C语言基础】:自定义类型(二) -->联合和枚举
文章目录
- 一、联合体
- 1.1 联合体类型的声明
- 1.2 联合体的特点
- 1.3 相同成员的结构体和联合体对比
- 1.4 联合体大小的计算
- 1.5 联合体练习
- 二、枚举类型
- 2.1 枚举类型的声明
- 2.2 枚举的优点
书山有路勤为径,学海无涯苦作舟。
创作不易,宝子们!如果这篇文章对你们有帮助的话,别忘了给个免费的赞哟~

一、联合体
1.1 联合体类型的声明
像结构体一样,联合体也是由一个或者多个成员构成,这些成员可以不同的类型。
但是编译器只为最大的成员分配足够的内存空间。联合体的特点是所有成员共用同一块内存空间。所以联合体也叫:共用体。
给联合体其中一个成员赋值,其他成员的值也跟着变化。
// 联合体的声明
union Un
{char c1;int i;
};
#include<stdio.h>
int main()
{union Un u = { 0 }; // 联合变量的定义printf("%zd\n", sizeof(u)); // 计算联合变量的大小return 0;
}

从运行结果来看:这个联合体中有两个成员变量,一个整形和一个字符型,按理说应该是5个字节的大小,但这个联合体的大小却只有4个字节,这也就是联合体的特点了。
1.2 联合体的特点
联合的成员是共用同一块内存空间的,这样⼀个联合变量的大小,至少是最大成员的大小(因为联合体至少得有能力保存最大的那个成员)。
【代码1】:
#include<stdio.h>
union Un
{char c1;int i;
};int main()
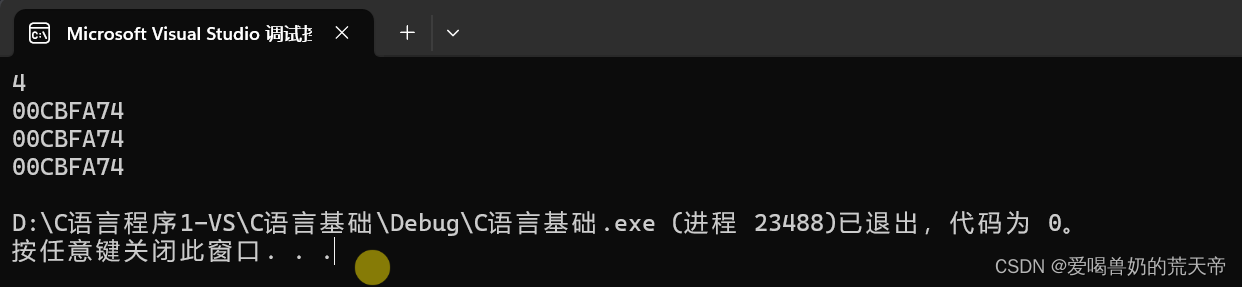
{union Un u = { 0 };printf("%zd\n", sizeof(u));printf("%p\n", &u);printf("%p\n", &(u.c1));printf("%p\n", &(u.i));return 0;
}
【代码2】:
#include<stdio.h>
union Un
{char c;int i;
};int main()
{union Un u = { 0 };u.i = 0x11223344;u.c = 0x55;printf("%x\n", u.i);return 0;
}
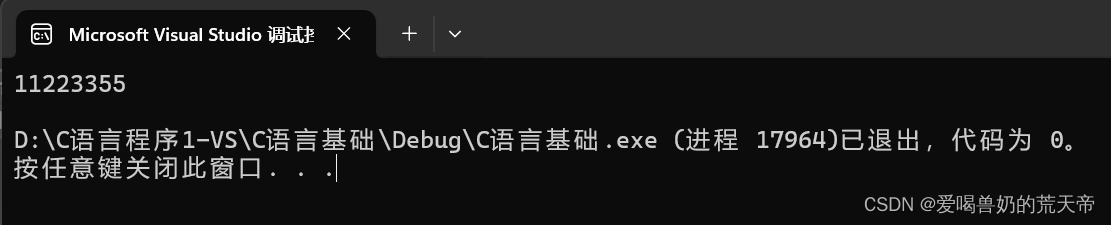
代码1输出的三个地址一模一样,代码2的输出,我们发现将i的第4个字节的内容修改为55了。
我们仔细分析就可以画出,un的内存布局图。
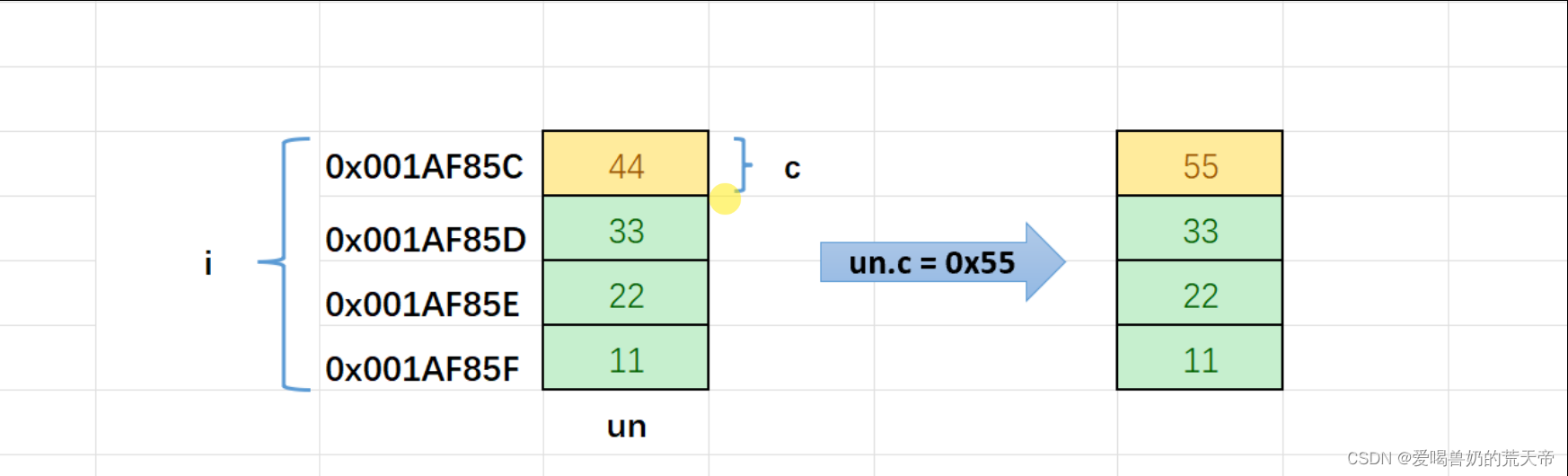
【结论】:联合体的成员是共用同一块内存空间的,修改一个其他的也会被修改。
1.3 相同成员的结构体和联合体对比
我们再对比一下相同成员的结构体和联合体的内存布局情况。
【结构体】:
struct S
{char c;int i;
};
struct S s = { 0 };
【联合体】:
union Un
{char c;int i;
};
union Un un = { 0 };

1.4 联合体大小的计算
- 联合的大小至少是最大成员的大小。
- 当最大成员大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。
#include<stdio.h>
union Un
{char c[5];int i;
};int main()
{union Un u = { 0 };printf("%zd\n", sizeof(u));return 0;
}
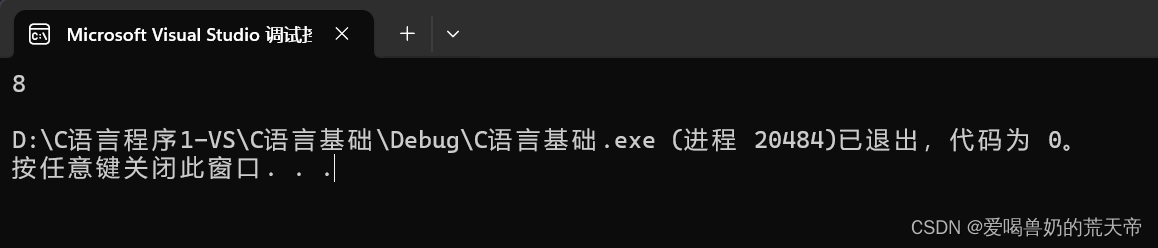
以这题为例,这个联合体中最大的成员是char c[5],但这个联合体的大小却并不是5个字节的大小,而是8个字节,这说明联合体的大小不全是最大成员的大小。当最大成员的大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。这里char c[5] 就相当于5个char 类型,也就是1个字节,VS的默认值是8,所以对齐数是1,int占4个字节,所以对齐数就是4,所以这个联合体的最大对齐数就是4,但5并不是4的倍数,即要浪费3个字节变为8个字节。
【结论】:联合体的大小也要是最大对齐数的倍数。
使用联合体是可以节省空间的,举例:
比如,我们要搞一个活动,要上线一个礼品兑换单,礼品兑换单中有三种商品:图书、杯子、衬衫。
每一种商品都有:库存量、价格、商品类型和商品类型相关的其他信息。
| 图书:书名、作者、页数
| 杯子:设计
| 衬衫:设计、可选颜色、可选尺寸
这题可以直接用结构体写:
struct gift_list
{// 公共属性int stock_number; // 库存量double price; // 价格int item_type; // 商品类型// 特殊属性char title[20]; // 书名char author[20]; // 作者int num_pages; // 页数char desgin[30]; // 设计int colors; // 颜色int sizes; // 尺寸
};
上述的结构其实设计的很简单,用起来也方便,但是结构的设计中包含了所有礼品的各种属性,这样使得结构体的大小就会偏大,比较浪费内存。因为对于礼品兑换单中的商品来说,只有部分属性信息是常用的。比如:
商品是图书,就不需要design、colors、sizes。
所以我们就可以把公共属性单独写出来,剩余属于各种商品本⾝的属性使用联合体起来,这样就可以介绍所需的内存空间,⼀定程度上节省了内存。
struct gift_list
{int stock_number; // 库存量double price; // 价格int item_type; // 商品类型union{struct {char title[20]; // 书名char author[20]; // 作者int num_pages; // 页数}book;struct{char desgin[30]; // 设计}mug;struct{char desgin[30]; // 设计int colors; // 颜色int sizes; // 尺寸}shirt;}item;
};
1.5 联合体练习
写⼀个程序,判断当前机器是大端?还是小端?
#include<stdio.h>
int check_sys()
{union Un{int i;char c;}u;u.i = 1;return u.c;
}int main()
{int ret = check_sys();if (ret == 1)printf("小端\n");elseprintf("大端\n");return 0;
}

二、枚举类型
2.1 枚举类型的声明
枚举顾名思义就是一一列举。
把可能的取值一一列举。
比如我们现实生活中:
| 一周的星期一到星期日是有限的7天,可以一一列举
| 性别有:男、女、保密,也可以一一列举
| 月份有12个月,也可以一一列举
| 三原色,也是可以意义列举
这些数据的表示就可以使用枚举了。
enum Day // 星期
{Mon,Tues,Wed,Thur,Fri,Sat,Sun
};enum Sex // 性别
{MALE,FEMALE,SECRET
};enum Color // 三原色
{RED,GREEN,BLUE
};
以上定义的 enum Day , enum Sex , enum Color 都是枚举类型。{} 中的内容是枚举类型的可能取值,也叫枚举常量 。
这些可能取值都是有值的,默认从0开始,依次递增1,当然在声明枚举类型的时候也可以赋初值。
enum Color // 三原色
{RED,GREEN,BLUE
};int main()
{enum Color color = RED;return 0;
}
枚举常量也是有值的。
#include<stdio.h>
enum Color // 三原色
{RED,GREEN,BLUE
};int main()
{printf("%d\n", RED);printf("%d\n", GREEN);printf("%d\n", BLUE);return 0;
}
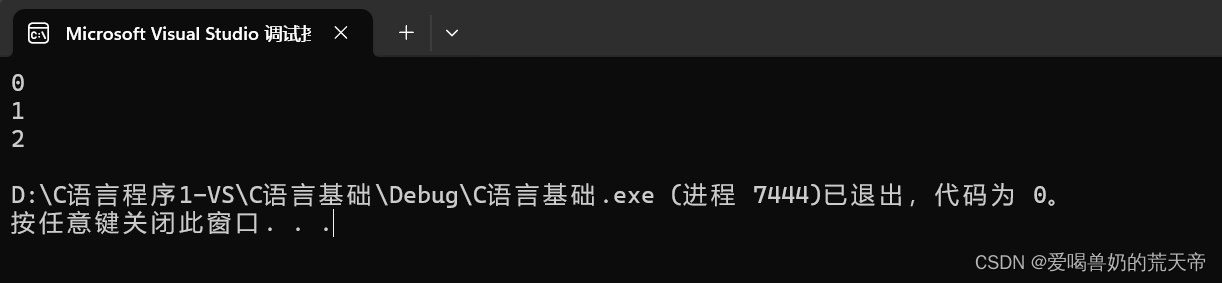
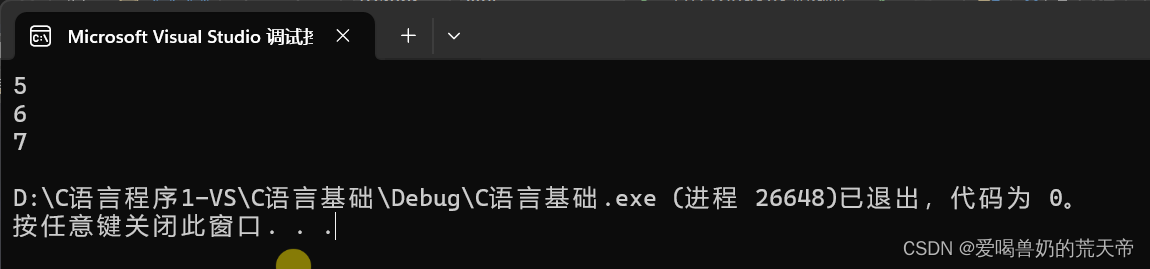
默认值从0开始,往后依次加一,也可以在声明枚举类型的时候也可以赋初值。
enum Color // 三原色
{RED = 5,GREEN,BLUE
};
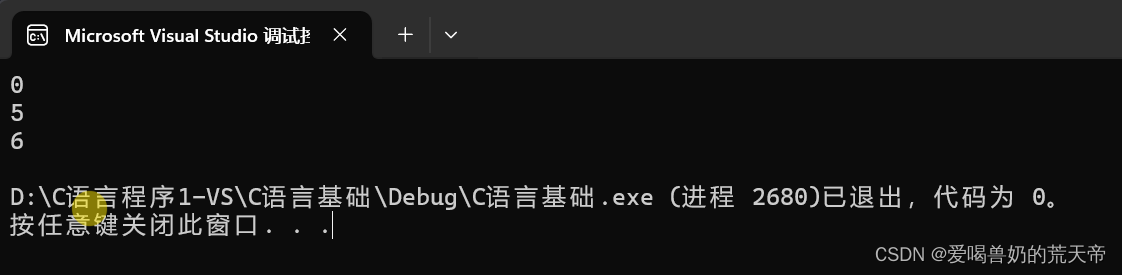
enum Color // 三原色
{RED,GREEN = 5,BLUE
};
2.2 枚举的优点
为什么使用枚举?
学到这里,我们会发现枚举常量和 #define 有点类似,那为什么不直接用 #define 呢?
enum Color // 三原色
{RED,// 0GREEN,// 1BLUE// 2
};#define RED 0
#define GREEN 1
#define BLUE 2
枚举的优点:
- 增加代码的可读性和可维护性
- 和 #define 定义的标识符比较枚举有类型检查,更加严谨。
- 便于调试,预处理阶段会删除 #define 定义的符号
- 使用方便,一次可以定义多个常量
- 枚举常量是遵循作用域规则的,枚举声明在函数内,只能在函数内使用
【示例】:计算器
enum Option
{EXIT,ADD,SUB,MUL,DIV
};int mian()
{int input = 0;printf("请选择:>");scanf("%d", &input);switch (input){case ADD: // 加法break;case SUB: // 减法break;case MUL: // 乘法break;case DIV: // 除法break;case EXIT: // 退出break;default:break;}return 0;
}
这样跟有利于我们代码的可读性。
注意:C语言中可以利用整数给枚举变量赋值,但是C++不可以,这是因为C++的类型检查比较严格。
enum Color // 三原色
{RED,// 0GREEN,// 1BLUE// 2
};int main()
{// enum Color color = RED; // TRUE enum Color color = 0;return 0;
}
enum Color color = 0; 这一句虽然在C语言中不会报错,但是在C++中会显示类型不同,无法赋值,就是因为C++的类型检查比较严格。
相关文章:

【C语言基础】:自定义类型(二) -->联合和枚举
文章目录 一、联合体1.1 联合体类型的声明1.2 联合体的特点1.3 相同成员的结构体和联合体对比1.4 联合体大小的计算1.5 联合体练习 二、枚举类型2.1 枚举类型的声明2.2 枚举的优点 书山有路勤为径,学海无涯苦作舟。 创作不易,宝子们!如果这篇…...

【授时防火墙】GPS北斗卫星授时信号安全防护装置系统
【授时防火墙】GPS北斗卫星授时信号安全防护装置系统 【授时防火墙】GPS北斗卫星授时信号安全防护装置系统 1、装置概述 卫星信号安全防护装置(以下简称“防护装置”)是一款专门针对卫星导航授时安全的设备。该设备能接收 BD 系统和 GPS 系统卫星信号&am…...
)
关于 MySQL 优化(详解)
文章目录 关于 MySQL 优化一、硬件方面的优化1、关于 CPU2、关于内存3、关于磁盘 二、MySQL 配置文件1、 default-time-zone8:002、interactive_timeout 1203、wait_timeout 1204、open_files_limit 102405、group_concat_max_len 1024006、usermysql7、character-set-serv…...

Hive详解(5)
Hive 窗口函数 案例 需求:连续三天登陆的用户数据 步骤: -- 建表 create table logins (username string,log_date string ) row format delimited fields terminated by ; -- 加载数据 load data local inpath /opt/hive_data/login into table log…...

阿里云效codeup如何执行github flow工作流
在阿里云效中执行 GitHub 工作流,实质上是在使用 Git 进行版本控制的过程中遵循 GitHub Flow 的原则。GitHub Flow 是一种简洁高效的工作流程,特别适用于追求快速迭代的团队。下面是在阿里云效中执行 GitHub 工作流的基本步骤: 1. 准备工作 …...

node.js的模块化 与 CommonJS规范
一、node.js的模块化 (1)什么是模块化? 将一个复杂的程序文件依据一定的规则拆分成为多个文件的过程就是模块化 在node.js中,模块化是指把一个大文件拆分成独立并且相互依赖的多个小模块,将每个js文件被认为单独的一个模块;模块…...
)
RK3588平台开发系列讲解(PWM开发篇)
目录 前⾔ 驱动文件 DTS 节点配置 PWM 流程 PWM 使⽤ 常⻅问题 PWM 在 U-Boot 与 kernel 之间的衔接问题 PWM Regulator 时 PWM pin 脚上下拉配置问题 前⾔ 脉宽调制( PWM , Pulse Width Modulation )功能在嵌⼊式系统中是⾮常常⻅的…...

宝塔面板操作一个服务器域名部署多个网站
此处记录IP一样,端口不一样的操作方式: 宝塔面板操作: 1、创建第一个网站: 网站名用IP地址,默认80端口。 创建好后,直接IP访问就可以了。看到自带的默认首页 2、接下来部署第二个网站: 仍然是…...

surfer绘制等值线图
surfer介绍 Surfer软件,是美国Golden Software公司编制的一款以画三维图的软件。该软件具有强大的插值功能和绘制图件能力,可用来处理XYZ数据,是地质工作者常用的专业成图软件(来源于百度百科)。 surfer可以用来绘制…...

免费开源的 AI 绘图工具 ImgPilot
免费开源的 AI 绘图工具 ImgPilot 分类 开源分享 项目名: ImgPilot -- 通过提示词及涂鸦生成图片 Github 开源地址: GitHub - leptonai/imgpilot: Turn the draft into amazing artwork with the power of Real-Time Latent Consistency Model 在线地址ÿ…...

Java系统架构设计:构建稳定高效的软件基石
在当今数字化时代,软件系统的稳定性、可扩展性和性能至关重要。Java作为一种广泛应用的编程语言,其系统架构设计对于软件的成功实施具有决定性的影响。本文将探讨Java系统架构设计的重要性以及设计过程中的关键要素。 首先,Java系统架构设计…...

【IntermLM2】学习笔记
微调方式 在大模型的下游应用中,可以有两种微调方式 增量续训 即无监督的方式,让模型学习一些新知识,比如某些垂直领域的新知识 使用的数据有:书籍,文章,代码等有监督微调 为了让模型学会理解指令进行对话…...
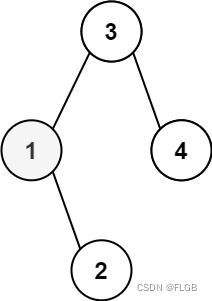
【二叉树】Leetcode 230. 二叉搜索树中第K小的元素【中等】
二叉搜索树中第K小的元素 给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。 示例1: 输入:root [3,1,4,null,2], k 1 输出:1 解…...

JS中常用的几种事件
在js中分为多种事件,比如点击事件,焦点事件,加载事件,鼠标事件等等... ... 点击事件 onclick点击事件,ondblclick双击事件 焦点事件 onblur元素失去焦点,onfocus元素获取焦点 加载事件 onload一个页面…...

Android WebView的使用与后退键处理
目录 前言首先,我们需要在布局文件中添加webView组件在Activity中获取webView实例,并加载网页内容 前言 webView是Android中常用的组件之一,用于展示网页内容。它可以加载HTML文件、URL链接等网页内容,并提供交互功能。在使用webV…...

【备忘录】Docker 2375远程端口安全漏洞解决
最近为了项目需要,把docker 的远程端口2375 给开放了。不出意外出意外了。没多久,网站报流量告警,第一反应就是开放2375这个端口问题导致,毫不迟疑直接切换服务器。关闭该台服务器的docker服务,并逐步清理掉挖矿进程&a…...
)
343. 整数拆分(力扣LeetCode)
文章目录 343. 整数拆分题目描述动态规划 343. 整数拆分 题目描述 给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k > 2 ),并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释:…...

Spring面试题系列-3
Spring框架是由于软件开发的复杂性而创建的。Spring使用的是基本的JavaBean来完成以前只可能由EJB完成的事情。然而,Spring的用途不仅仅限于服务器端的开发。从简单性、可测试性和松耦合性角度而言,绝大部分Java应用都可以从Spring中受益。 Spring的属性…...

【比特币】比特币的奥秘、禁令的深层逻辑与风云变幻
导语: 比特币(Bitcoin),这个充满神秘色彩的数字货币,自诞生以来便成为各界瞩目的焦点。它背后所蕴含的Mining机制、禁令背后的深层逻辑以及市场的风云变幻,都让人欲罢不能。今天,我们将深入挖掘比特币的每一个角落&…...
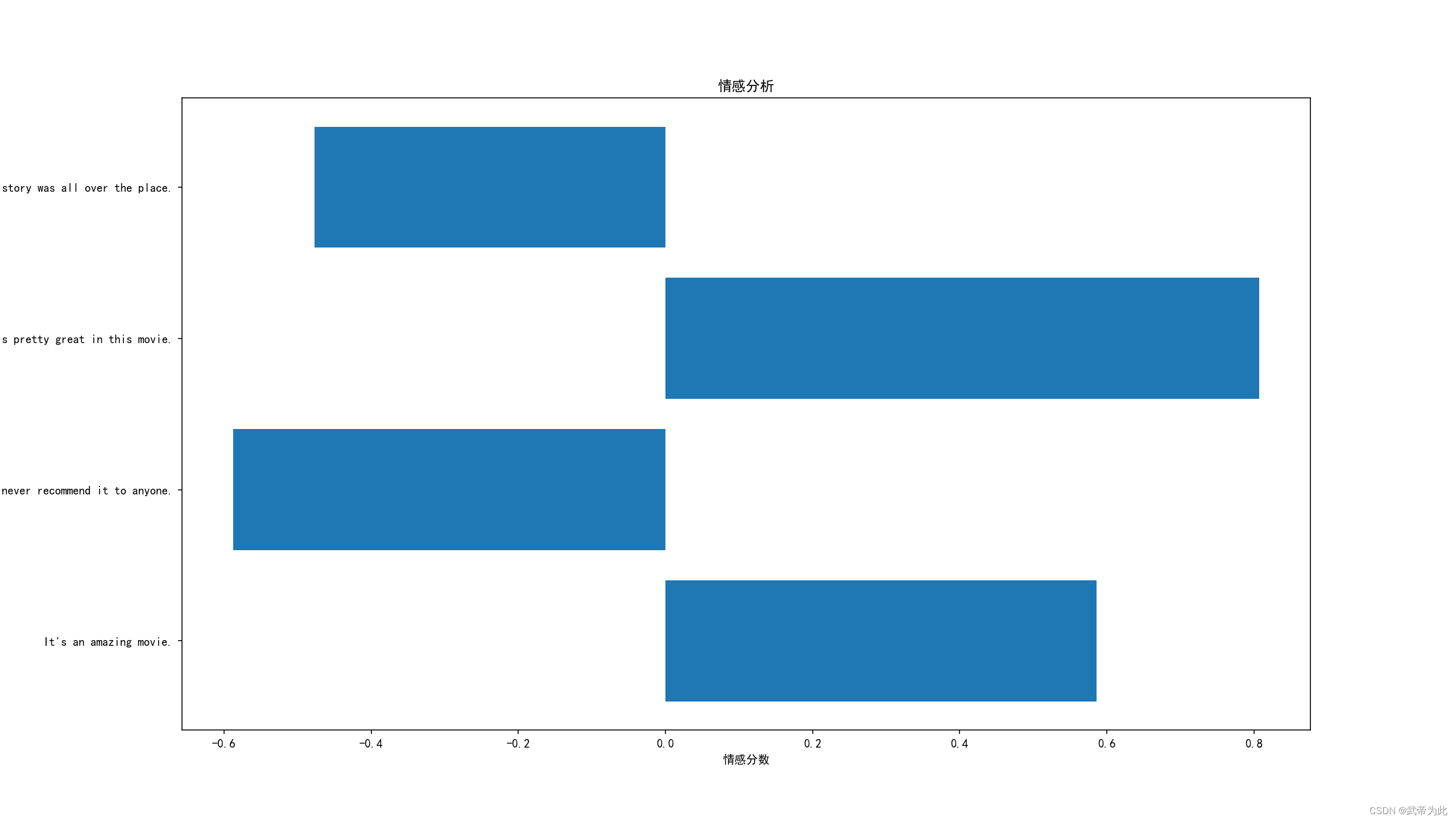
【情感分析概述】
文章目录 一、情感极性分析概述1. 定义2. 情感极性的类别3. 应用场景 二、情感极性分析的技术方法1. 基于规则的方法a. 关键词打分b. 情感词典的使用 2. 基于机器学习的方法a. 监督学习方法b. 深度学习方法 三、Python进行情感极性分析 一、情感极性分析概述 情感极性分析&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

