[蓝桥杯 2022 省 B] 李白打酒加强版
题目链接
[蓝桥杯 2022 省 B] 李白打酒加强版
题目描述
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2 2 2 斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N N N 次,遇到花 M M M 次。已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒( 0 0 0 斗)时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入格式
第一行包含两个整数 N N N 和 M M M。
输出格式
输出一个整数表示答案。由于答案可能很大,输出模 1000000007 1000000007 1000000007(即 1 0 7 + 7 10^7 + 7 107+7 ) 的结果。
输入输出样例
输入
5 10
输出
14
数据范围
- 1 ≤ n , m ≤ 100 1 \leq n, m \leq 100 1≤n,m≤100
解法:动态规划
我们定义 f ( i , j , k ) f(i,j,k) f(i,j,k) 为 遇到店 i i i 次,遇到花 j j j 次,酒壶里有 k k k 斗酒的方案数。
我们最终要返回的是 遇到店 n n n次, 遇到花 m m m 次 且最后一次遇到的是花,酒壶里有 0 0 0 斗酒的方案数。
实际上,它等价于 遇到店 n n n次, 遇到花 m − 1 m - 1 m−1 次 ,酒壶里有 1 1 1 斗酒的方案数。因为这样保证了最后一次是遇到花的,两者实际等价,即 f ( n , m − 1 , 1 ) f(n, m - 1, 1) f(n,m−1,1)。
由于 m m m 不超过 100 100 100,那么 k k k 也不超过 100 100 100,否则喝不完酒。
我们直接讨论当前遇到的是店,还是花:
- 如果当前遇到的是店,那么 f [ i ] [ j ] [ k ] = f [ i ] [ j ] [ k ] + f [ i − 1 ] [ j ] [ k / 2 ] f[i][j][k] = f[i][j][k] + f[i - 1][j][k / 2] f[i][j][k]=f[i][j][k]+f[i−1][j][k/2],这里需要保证 i > 0 i > 0 i>0 且 k m o d 2 = 0 k \ mod\ 2 = 0 k mod 2=0;
- 如果当前遇到的是花,那么 f [ i ] [ j ] [ k ] = f [ i ] [ j ] [ k ] + f [ i ] [ j − 1 ] [ k + 1 ] f[i][j][k] = f[i][j][k] + f[i][j-1][k+1] f[i][j][k]=f[i][j][k]+f[i][j−1][k+1],这里需要保证 j > 0 j > 0 j>0;
初始 f [ 0 ] [ 0 ] [ 2 ] = 1 f[0][0][2] = 1 f[0][0][2]=1,表示最开始酒壶里有 2 2 2 斗酒。
最终返回的答案就是 f [ n ] [ m − 1 ] [ 1 ] f[n][m-1][1] f[n][m−1][1]。
时间复杂度: O ( n × m × k ) O(n \times m \times k) O(n×m×k)
C++代码:
#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <unordered_set>
#include <set>
#include <algorithm>using namespace std;
using LL = long long;const int MOD = 1e9 + 7;
const int N = 110;LL f[N][N][N];void solve(){int n, m;cin>>n>>m;f[0][0][2] = 1;for(int i = 0;i <= n;i++){for(int j = 0;j < m;j++){if(i == 0 && j == 0) continue; for(int k = 0;k <= 100;k++){if(k % 2 == 0 && i) f[i][j][k] += f[i - 1][j][k / 2];//操作1if(j) f[i][j][k] += f[i][j - 1][k + 1];//操作2f[i][j][k] %= MOD;}}}cout<<f[n][m - 1][1];
}int main(){int t = 1;//cin>>t;while(t--){solve();}return 0;
}
Java代码:
import java.util.*;
import java.io.*;public class Main
{static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));static final int N = 110;static final int MOD = 1000_000_007;public static void main(String[] args) throws Exception{String[] strs = reader.readLine().split(" ");int n = Integer.parseInt(strs[0]);int m = Integer.parseInt(strs[1]);int[][][] f = new int[N][N][N];f[0][0][2] = 1;for(int i = 0;i <= n;i++){for(int j = 0;j <= m;j++){if(i == 0 && j == 0) continue;for(int k = 0;k <= 100;k++){if(k % 2 == 0 && i > 0) f[i][j][k] += f[i - 1][j][k / 2];if(j > 0) f[i][j][k] += f[i][j - 1][k + 1];f[i][j][k] %= MOD;}}}System.out.println(f[n][m - 1][1]);}
}
相关文章:

[蓝桥杯 2022 省 B] 李白打酒加强版
题目链接 [蓝桥杯 2022 省 B] 李白打酒加强版 题目描述 话说大诗人李白,一生好饮。幸好他从不开车。 一天,他提着酒壶,从家里出来,酒壶中有酒 2 2 2 斗。他边走边唱: 无事街上走,提壶去打酒。 逢店加一倍…...
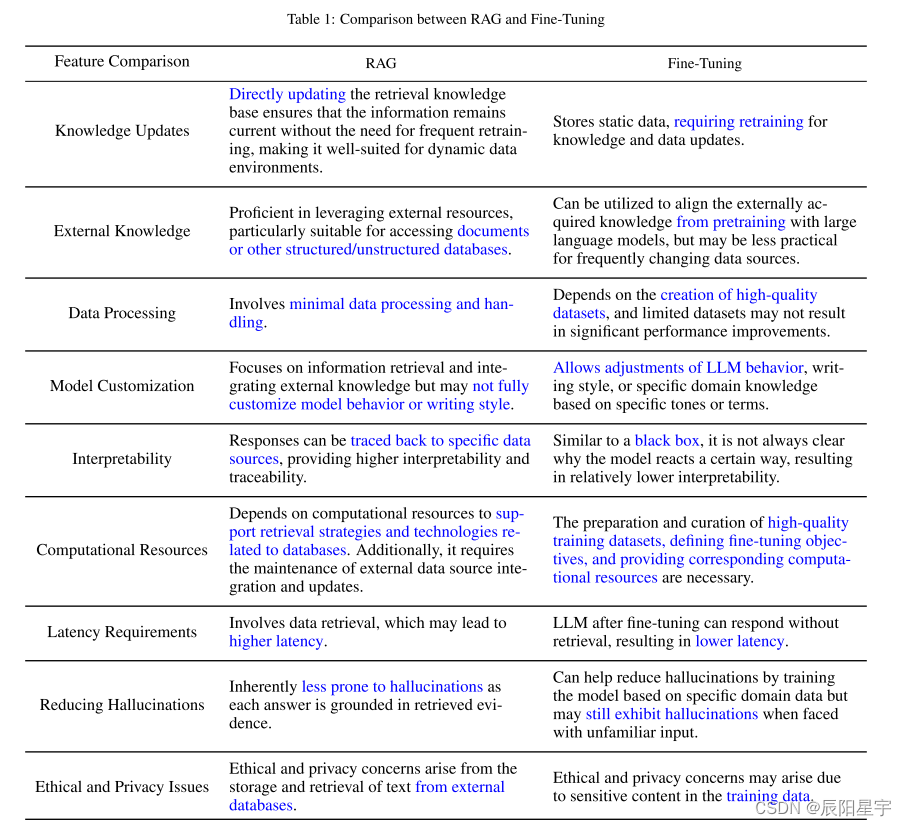
【检索增强】Retrieval-Augmented Generation for Large Language Models:A Survey
本文简介 1、对最先进水平RAG进行了全面和系统的回顾,通过包括朴素RAG、高级RAG和模块化RAG在内的范式描述了它的演变。这篇综述的背景下,更广泛的范围内的法学硕士研究RAG的景观。 2、确定并讨论了RAG过程中不可或缺的核心技术,特别关注“…...
EVM Layer2 主流解决方案
深度解析主流 EVM Layer 2 解决方案:zk Rollups 和 Optimistic Rollups 随着以太坊网络的不断演进和 DeFi 生态系统的迅速增长,以太坊 Layer 2 解决方案日益受到关注。 其中,zk Rollups 和 Optimistic Rollups 作为两种备受瞩目的主流 EVM&…...

go中结构体标签:omitempty、json꞉“name“、 gorm꞉“column꞉name“、yaml꞉“name“
在Go语言中,结构体标签(Struct Tags)提供了一种在编译时附加到结构体字段上的元数据,这些标签可以被运行时的反射(reflection)机制读取。结构体标签的存在意义和用途非常广泛,主要包括ÿ…...

七月论文审稿GPT第4版:通过paper-review数据集微调Mixtral-8x7b,对GPT4胜率超过80%
前言 在此之前,我司论文审稿项目组已经通过我司处理的paper-review数据集,分别微调了RWKV、llama2、gpt3.5 16K、llama2 13b、Mistral 7b instruct、gemma 7b 七月论文审稿GPT第1版:通过3万多篇paper和10多万的review数据微调RWKV七月论文审…...

【QT学习】1.qt初识,创建qt工程,使用按钮,第一个交互按钮
1.初识qt--》qt是个框架,不是语言 1.学习路径 一 QT简介 ,QTCreator ,QT工程 ,QT的第一个程序,类,组件 二 信号与槽 三 对话框 四 QT Desiner 控件 布局 样式 五 事件 六 GUI绘图 七 文件 八 …...

JavaScript_与html结合方式
JavaScript_语法 ECMAScript:客户端脚本语言的标准 1.基本语法 1.1 与html结合方式(2种) 1. 内部JS 定义<script>,标签体内容就是js代码 2. 外部JS 定义<script>,通过src属性引入外部的 js文件 注意: 1.<script>…...

WPF —— 动画
wpf动画类型 1<类型>Animation这些动画称为from/to/by动画或者叫基本动画,他们会在起始值或者结束值进行动画处理,常用的例如 <DoubleAnimation> 2 <类型>AnimationUsingKeyFrames: 关键帧动画,功能要比from/to这些动画功…...

前端二维码生成工具小程序:构建营销神器的技术解析
摘要: 随着数字化营销的不断深入,二维码作为一种快速、便捷的信息传递方式,已经广泛应用于各个领域。本文旨在探讨如何通过前端技术构建一个功能丰富、操作简便的二维码生成工具小程序,为企业和个人提供高效的营销支持。 一、引言…...

光伏发电量预测(Python代码,CNN结合LSTM,TensorFlow框架)
1.数据集(开始位置),数据集免费下载链接:https://download.csdn.net/download/qq_40840797/89051099 数据集一共8列,第一列是时间,特征列一共有6列:"WindSpeed" - 风速 "Sunshi…...

GPT带我学-设计模式11-组合模式
设计模式类型 结构型设计模式 使用场景 将对象组合成树状结构来表现"部分-整体"的层次结构。这种模式能够使得客户端对单个对象和组合对象的使用具有一致性。这句话太抽象了,拿一个实际的网站菜单树例子来说。 例子:网页菜单树 一个网站的…...

Centos7 elasticsearch-7.7.0 集群搭建,启用x-pack验证 Kibana7.4用户管理
前言 Elasticsearch 是一个分布式、RESTful 风格的搜索和数据分析引擎,能够解决不断涌现出的各种用例。 作为 Elastic Stack 的核心,它集中存储您的数据,帮助您发现意料之中以及意料之外的情况。 环境准备 软件 …...

[CSS]中子元素在父元素中居中
元素居中 对于当行文字居中,比较简单,设置text-align:center和text-height为盒子高度即可 对于父元素中子元素居中,要实现的话有以下几个方法 方法1:利用定位margin:auto <style>.father {width: 500px;heig…...

电脑突然死机怎么办?
死机是电脑常见的故障问题,尤其是对于老式电脑来说,一言不合电脑画面就静止了,最后只能强制关机重启。那么你一定想知道是什么原因造成的吧,一般散热不良最容易让电脑死机,还有系统故障,比如不小心误删了系…...

Kyligence 正式加入华为“同舟共济”行动计划,成为行业数智化“联盟级伙伴”
让“生态飞轮”旋转让“生态飞轮”旋转3月14日至15日,华为中国合作伙伴大会 2024 在深圳召开。本次大会以“因聚而生,数智有为”为主题,皆在升级“伙伴华为”数智体系,共筑解决方案竞争力,共赢数智世界新机遇。Kyligen…...

大模型推理框架——text-generation-inference
项目地址:https://github.com/huggingface/text-generation-inference 安装 安装rust curl --proto =https --tlsv1.2 -sSf https://sh.rustup.rs | sh安装 Protoc PROTOC_ZIP=protoc-21.12-linux-x86_64.zip curl -OL https://github.com/protocolbuffers/protobuf/relea…...

电梯四种事故检测YOLOV8
电梯四种事故检测,采用YOLOV8训练得到PT模型,然后转换成ONNX,OPENCV调用,支持C/PYTHON/ANDORID开发 电梯四种事故检测YOLOV8...

构建docker环境下的thunder迅雷插件
前言 从迅雷群晖套件中提取出来用于其他设备的迅雷远程下载服务程序。仅供测试,测试完请大家自觉删除。 下载保存目录 /xunlei/downloads, 对应迅雷应用内显示的下载路径是 /downloads 或者 /迅雷下载 仓库 阿里云镜像(国内访问ÿ…...
Django开发复盘
一、URL 对于一个不会写正则表达式的蒟蒻来说,在urls.py中就只能傻傻的写死名字,但是即便这样,还会有很多相对路径和绝对路径的问题(相对ip端口的路径),因为我们网页中涉及到页面跳转,涉及到发送…...
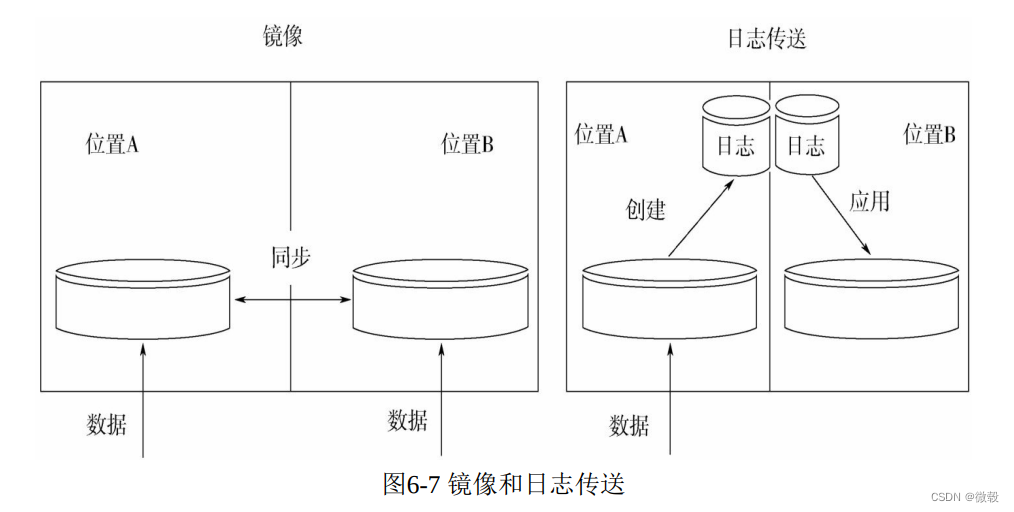
第6章 数据存储操作
思维导图 6.1 引言 数据存储与操作包括对存储数据的设计、实施和支持,最大化实现数据资源的价值,贯穿于数据创建/获取到处置的整个生命周期。 6.1.1 业务驱动因素 数据存储与操作活动对于依赖数据的企业来说非常关键,这些活动的主要驱动因素是…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
