视觉里程计之对极几何
视觉里程计之对极几何
前言
上一个章节介绍了视觉里程计关于特征点的一些内容,相信大家对视觉里程计关于特征的描述已经有了一定的认识。本章节给大家介绍视觉里程计另外一个概念,对极几何。
对极几何
对极几何是立体视觉中的几何关系,描述相机从不同位置拍摄3D场景时,3D点与相机位姿,图像观测像素坐标之间的几何关系。这种几何关系可以作为约束应用到求解相机运动及特征点3D坐标中。
立体视觉(Stereo Vision)是什么呢?我们可以这样理解:
立体视觉(StereoVision) = 寻找相关性(Correspondences) + 重建(Reconstruction)
● Correspondences:给定张图片中的像素P点,寻找其在另一张图片中的对应点Pr。
● Reconstruction:给定一组对应点对(P,P,),计算其在空间中对应点P的3D坐标。
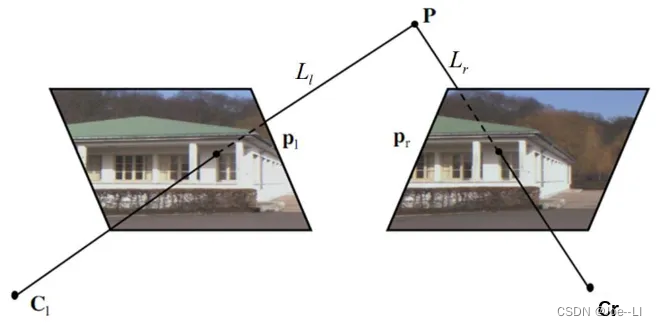
对极几何中存在以下几个概念:对极点,对极线,对极平面。其中对极线构成的约束称为对极线约束,也称为对极约束。
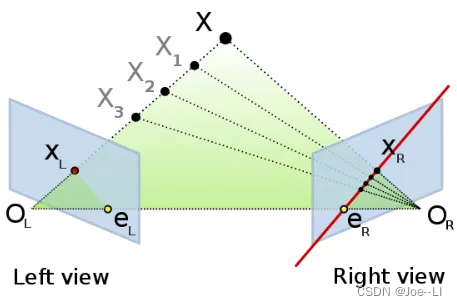
对极点:左相机光心OL在右相机平面上的成像点eR,称为其中一个对极点,类似的,OR在左相机上的成像点eL,也是对极点。对极点是虚拟的点,如果相机之间不能观测到对方光心,则对极点会在图像之外。
对极线:在相机OL观测到一个点XL,实际情况该XL可能对应3D坐标中任意一个Xi,因为线OLX被因为与左相机中心重合而被左相机视为一个点。但对于右相机,每个Xi则将有不同观测,这些观测为其图像平面中的一条线,该线称为对极线。如图,右摄像机中的那条线(eRXR)就称为对极线。对称地,右相机视线ORX为一个点,而被左相机视为对极线(eLXL)。
对极线是3D空间中点X的位置的函数,一个兴趣点对应一组对极线(XLeL,XReR)。由于线OLX通过透镜OL的光学中心,因此右图中相应的对极线必须通过eR(并且对应于左图中的极线)。一幅图像中的所有对极线都包含该图像的对极点。
对极平面:趣点X与两相机中心OL、OR三点形成的平面称为对极平面。对极平面与每个相机的图像平面相交形成线即为对极线。无论X位于何处,所有对极平面和对极线都与对极点相交。
基线:两个相机光心相连的直线OLOR称为基线
对极约束
P点在图像I1中观测的位置是P1,在I2中观测的位置是P2,O1与O2为相机的光心。点P与O1,O2形成的平面称为极平面。极平面与图像平面的交线称为极线,即图中的l1与l2。其中e1与e2称为极点。
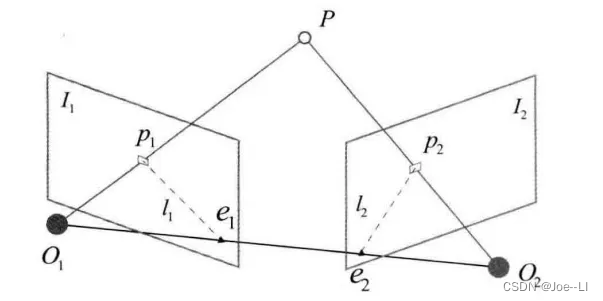
假设O1相机坐标系下P点坐标为P(X,Y,Z),归一化坐标为Pu(X1,Y1,1),则根据针孔相机投影模型,观测的像素坐标P1(u1,v1)为:
[ u 1 v 1 1 ] = [ f x 0 c x 0 f y c y 0 0 1 ] [ X 1 X 1 1 ] \ \left[\begin{matrix}u_1\\v_1\\1\\\end{matrix}\right] =\ \left[\begin{matrix}f_x&0&c_x\\0&f_y&c_y\\0&0&1\\\end{matrix}\right] \ \left[\begin{matrix}X_1\\X_1\\1\\\end{matrix}\right] u1v11 = fx000fy0cxcy1 X1X11
化为简洁的形式如下,其中K为相机内参:
p 1 = K P u 1 p_1=KP_u^1 p1=KPu1
好了,现在假设O1相机相对于O2的运动及旋转为t与R,那么根据坐标系变换的关系,P在O2坐标系下坐标为:
P 2 = R P 1 + t P_2=RP_1+t P2=RP1+t
同样,根据相机投影模型,可以得到观测像素坐标与局部三维坐标的关系为:
p 2 = K P u 2 = K ( R P 1 + t ) u p_2=KP_u^2=K(RP_1+t)_u p2=KPu2=K(RP1+t)u
为了描述对极约束,这里需要用到投影关系,即一个坐标等比例缩放的关系,物理含义是指它们是在同一条射线上,通过投影关系,可以得到在相机O1与O2下,对P点观测的归一化坐标关系为:
p u 2 ∗ 1 s 2 = R p u 1 ∗ 1 s 1 + t p_u^2\ast\frac{1}{s_2}=Rp_u^1\ast\frac{1}{s_1}+t pu2∗s21=Rpu1∗s11+t
在等式左右同时左乘t^,上三角符号含义为取向量的反对称矩阵,运算结果为向量的外积,因为相同向量,外积为0,所以上式变为
t ∧ ∗ p u 2 ∗ 1 s 2 = t ∧ R p u 1 ∗ 1 s 1 t^\land\ast p_u^2\ast\frac{1}{s_2}=t^\land Rp_u^1\ast\frac{1}{s_1} t∧∗pu2∗s21=t∧Rpu1∗s11
两边同时乘以p2的转置
( p u 2 ) T ∗ t ∧ ∗ p u 2 ∗ 1 s 2 = ( p u 2 ) T ∗ t ∧ R p u 1 ∗ 1 s 1 \left(p_u^2\right)^T\ast t^\land\ast p_u^2\ast\frac{1}{s_2}=\left(p_u^2\right)^{T{\ast\ t}^\land}Rp_u^1\ast\frac{1}{s_1} (pu2)T∗t∧∗pu2∗s21=(pu2)T∗ t∧Rpu1∗s11
其中左等式,t^p2u为一个与t及p2u垂直的向量(所以对极几何t一定不能为0,不然在推导这里就不成立),既然与自身垂直,那么两个垂直向量做内积,结果为0,左侧严格等于0。则此时去掉常数项也不会影响等式成立
( p u 2 ) T t ∧ R p u 1 = 0 \left(p_u^2\right)^Tt^\land Rp_u^1=0 (pu2)Tt∧Rpu1=0
其中p1u,p2u为物体在相机坐标系下的归一化坐标,其与物体真实坐标及像素的齐次坐标关系为:
P u 1 = K − 1 u 1 齐 = s 1 P 1 P_u^1=K^{-1}u_1^齐=s_1P^1 Pu1=K−1u1齐=s1P1
通常有如下表示:
E = t ∧ R E=t^\land R E=t∧R
称E为对极几何中的本质矩阵(Essential Matrix),如果把物体的归一化坐标换为像素齐次坐标,则有如下结果:
u 2 齐 K − T t ∧ R K − 1 u 1 齐 = 0 u_2^齐K^{-T}t∧RK^{-1}u_1^齐=0 u2齐K−Tt∧RK−1u1齐=0
其中有如下表示:
F = K − T E K − 1 F=K^{-T}EK^{-1} F=K−TEK−1
F包含内参,称为对极几何中的基础矩阵(Fundamental Matrix).
本质矩阵的求解-八点法
由上可知,一对匹配点,与本质矩阵的关系可以得到一个等式:
( p u 2 ) T E p u 1 = 0 \left(p_u^2\right)^TEp_u^1=0 (pu2)TEpu1=0
其中E矩阵为3x3矩阵,有9个未知数,但实际上E只有5个自由度,表明其最少可以用五个点来列方程来求解,但这五个自由度是建立在非线性性质之上的,求解比较复杂。如果只考虑其尺度等价性,则E有8个自由度,这种线性性质会让求解更简单些,所以就有了常用的8点法。设E为:
E = [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] E\ =\ \left[\begin{matrix}e_1&e_2&e_3\\e_4&e_5&e_6\\e_7&e_8&e_9\\\end{matrix}\right] E = e1e4e7e2e5e8e3e6e9
则对极约束可以写为如下形式:
[ x 2 y 2 1 ] [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] [ x 1 y 1 1 ] = 0 \left[\begin{matrix}x_2&y_2&1\\\end{matrix}\right]\left[\begin{matrix}e_1&e_2&e_3\\e_4&e_5&e_6\\e_7&e_8&e_9\\\end{matrix}\right]\left[\begin{matrix}x_1\\y_1\\1\\\end{matrix}\right]\ =\ 0 [x2y21] e1e4e7e2e5e8e3e6e9 x1y11 = 0
把E写为向量形式:
e = [ e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 ] T e=\left[\begin{matrix}e_1&e_2&e_3\\\end{matrix}\ \ \ \begin{matrix}e_4&e_5&e_6\\\end{matrix}\ \ \ \begin{matrix}e_7&e_8&e_9\\\end{matrix}\right]^T e=[e1e2e3 e4e5e6 e7e8e9]T
则上式方程为:
[ x 2 x 1 x 2 y 1 x 2 y 2 x 1 y 2 y 1 y 2 x 1 y 1 1 ] ∗ e = 0 \left[\begin{matrix}x_2x_1&x_2y_1&x_2\\\end{matrix}\ \ \ \begin{matrix}y_2x_1&y_2y_1&y_2\\\end{matrix}\ \ \ \begin{matrix}x_1&y_1&1\\\end{matrix}\right]\ast e\ =\ 0 [x2x1x2y1x2 y2x1y2y1y2 x1y11]∗e = 0
使用8对匹配点,每一对匹配点构成上述的方程,那么就有8组方程,最后8组方程构成一个线性齐次方程组,这种将本质矩阵看做向量,然后通过求解线性方程组来获得矩阵的方式,也称为直接线性变换法(DLT)。如下:
( x 2 1 x 1 1 x 2 1 y 1 1 x 2 1 y 2 1 x 1 1 y 2 1 y 1 1 y 2 1 x 1 1 y 1 1 1 x 2 2 x 1 2 x 2 2 y 1 2 x 2 2 y 2 2 x 1 2 y 2 2 y 1 2 y 2 2 x 1 2 y 1 2 1 . . . x 2 8 x 1 8 x 2 8 y 1 8 x 2 8 y 2 8 x 1 8 y 2 8 y 1 8 y 2 8 x 1 8 y 1 8 1 ) e = 0 \left(\begin{array}{ccccccccc} x_{2}^{1} x_{1}^{1} & x_{2}^{1} y_{1}^{1} & x_{2}^{1} & y_{2}^{1} x_{1}^{1} & y_{2}^{1} y_{1}^{1} & y_{2}^{1} & x_{1}^{1} & y_{1}^{1} & 1 \\ x_{2}^{2} x_{1}^{2} & x_{2}^{2} y_{1}^{2} & x_{2}^{2} & y_{2}^{2} x_{1}^{2} & y_{2}^{2} y_{1}^{2} & y_{2}^{2} & x_{1}^{2} & y_{1}^{2} & 1 \\ & ... \\\ x_{2}^{8} x_{1}^{8} & x_{2}^{8} y_{1}^{8} & x_{2}^{8} & y_{2}^{8} x_{1}^{8} & y_{2}^{8} y_{1}^{8} & y_{2}^{8} & x_{1}^{8} & y_{1}^{8} & 1 \end{array}\right) e=0 x21x11x22x12 x28x18x21y11x22y12...x28y18x21x22x28y21x11y22x12y28x18y21y11y22y12y28y18y21y22y28x11x12x18y11y12y18111 e=0
根据线性方程解的情况,左侧系数矩阵为8x9的矩阵,e一定存在非零解。求解该方程,就可以得到本质矩阵E的每个元素了。
从本质矩阵恢复相机运动
在得到本质矩阵E之后,还需要从E中恢复相机的运动R与t。此时需要用到奇异值分解(SVD),假设E的SVD为:
E = U ∑ V T E=U\sum V^T E=U∑VT
其中U与V为正交阵,∑为奇异值矩阵。有如下性质:∑ = diag(σ,σ,0)。于是可以配凑出t与R
t 1 ∧ = U R z ( π 2 ) ∑ V T , R 1 = U R z T ( π 2 ) V T t 2 ∧ = U R z ( − π 2 ) ∑ V T , R 2 = U R z T ( − π 2 ) V T \begin{array}{c} t_{1}^{\wedge}=U R_{z}\left(\frac{\pi}{2}\right) \sum V^{\mathrm{T}}, R_{1}=U R_{z}^{T}\left(\frac{\pi}{2}\right) V^{T} \\ t_{2}^{\wedge}=U R_{z}\left(-\frac{\pi}{2}\right) \sum V^{\mathrm{T}}, R_{2}=U R_{z}^{T}\left(-\frac{\pi}{2}\right) V^{T} \end{array} t1∧=URz(2π)∑VT,R1=URzT(2π)VTt2∧=URz(−2π)∑VT,R2=URzT(−2π)VT
其中:
R z ( π 2 ) = [ 0 − 1 0 1 0 0 0 0 1 ] , R z ( − π 2 ) = [ − 0 1 0 1 0 0 0 0 1 ] R_z\left(\frac{\pi}{2}\right)=\ \left[\begin{matrix}0&-1&0\\1&0&0\\0&0&1\\\end{matrix}\right],R_z\left(-\frac{\pi}{2}\right)=\ \left[-\begin{matrix}0&1&0\\1&0&0\\0&0&1\\\end{matrix}\right] Rz(2π)= 010−100001 ,Rz(−2π)= −010100001
由于E与-E的等价,这里t取负号也是成立的,所以一共有四组解:
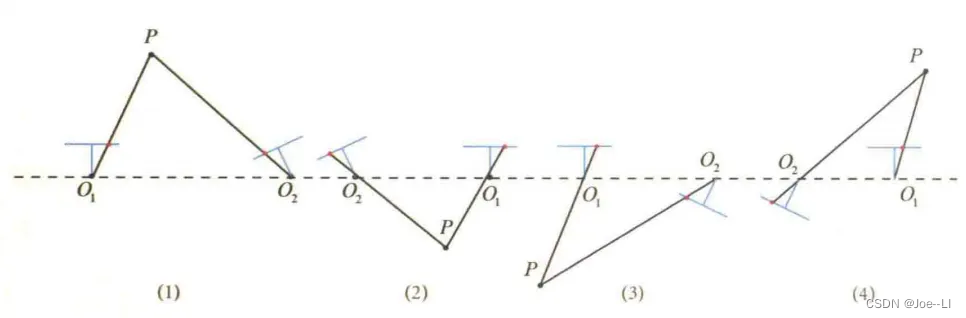
其中只有第一种情况,P点在两个相机下具有正的深度,所以只要把任意一点求解出深度,在两个相机坐标系下深度都为正,就可以得到真实解了。
单应矩阵
多视图几何中,除了本质矩阵和基础矩阵,还存在另一种常见的矩阵:单应矩阵(Homography)H,它描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上(比如墙、地面等),则可以通过单应性进行运动估计。这种情况在无人机携带的俯视相机或扫地机携带的顶视相机中比较常见。
单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。
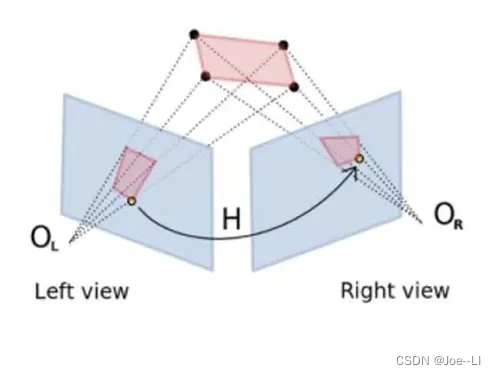
单应性在SLAM中具有重要意义。当特征点共面或者相机发生纯旋转时,基础矩阵的自由度下降,这就出现了所谓的退化(degenerate)。现实中的数据总包含一些噪声,这时如果继续使用八点法求解基础矩阵,基础矩阵多余出来的自由度将会主要由噪声决定。为了能够避免退化现象造成的影响,通常我们会同时估计基础矩阵F和单应矩阵H,选择重投影误差比较小的那个作为最终的运动估计矩阵。
单应矩阵的求解
如果特征点都在一个平面上,即点P满足:
n T P + d = 0 n^TP+d=0 nTP+d=0
那么有:
− n T P d = 1 -\frac{n^TP}{d}\ =\ 1 −dnTP = 1
这里的平面,指在O1坐标系下的平面,借助这个平面模型,按照推导基础矩阵约束过程类似,在O2中对P点观测的齐次坐标为:
p 2 = s 2 K ( R P 1 + t ) = s 2 K ( R P 1 + t ( − n T P 1 d ) ) p_2=s_2K\left(RP_1+t\right)=s_2K\left(RP_1+t\left(-\frac{n^TP_1}{d}\right)\right) p2=s2K(RP1+t)=s2K(RP1+t(−dnTP1))
= s 2 K ( R − t n T d ) P 1 =s_2K\left(R-\frac{tn^T}{d}\right)P_1 =s2K(R−dtnT)P1
= s 2 K ( R − t n T d ) 1 s 1 K − 1 p 1 =s_2K\left(R-\frac{tn^T}{d}\right){\frac{1}{s_1}K}^{-1}p_1 =s2K(R−dtnT)s11K−1p1
使用相机内参进行坐标转换时,如果只有内参K,那么点的坐标为物体归一化坐标到像素坐标,如果带深度或者比例系数s,则为物体实际坐标到像素坐标转换。记p2与p1之间的转换矩阵为H,则有
p 2 = H p 1 p_2=Hp_1 p2=Hp1
即:
( x 2 y 2 1 ) = ( h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 ) ( x 1 y 1 1 ) \left(\begin{matrix}x_2\\y_2\\1\\\end{matrix}\right)\ =\ \left(\begin{matrix}h_1&h_2&h_3\\h_4&h_5&h_6\\h_7&h_8&h_9\\\end{matrix}\right)\left(\begin{matrix}x_1\\y_1\\1\\\end{matrix}\right) x2y21 = h1h4h7h2h5h8h3h6h9 x1y11
由于p2与坐标转换后的p1在同一条射线上,所以等式右边乘以任意非零常数仍然成立。这里可以通过系数调整,使h9为1,于是上述方程,可以整理得如下等式:
u 2 = h 1 u 1 + h 2 v 1 + h 3 h 7 u 1 + h 8 v 1 + h 9 v 2 = h 4 u 1 + h 5 v 1 + h 6 h 7 u 1 + h 8 v 1 + h 9 \begin{array}{l} u_{2}=\frac{h_{1} u_{1}+h_{2} v_{1}+h_{3}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \\ v_{2}=\frac{h_{4} u_{1}+h_{5} v_{1}+h_{6}}{h_{7} u_{1}+h_{8} v_{1}+h_{9}} \end{array} u2=h7u1+h8v1+h9h1u1+h2v1+h3v2=h7u1+h8v1+h9h4u1+h5v1+h6
h 1 u 1 + h 2 v 1 + h 3 − h 7 u 1 u 2 − h 8 v 1 u 2 = u 2 h 4 u 1 + h 5 v 1 + h 6 − h 7 u 1 v 2 − h 8 v 1 v 2 = v 2 \begin{array}{l} h_{1} u_{1}+h_{2} v_{1}+h_{3}-h_{7} u_{1} u_{2}-h_{8} v_{1} u_{2}=u_{2} \\ h_{4} u_{1}+h_{5} v_{1}+h_{6}-h_{7} u_{1} v_{2}-h_{8} v_{1} v_{2}=v_{2} \end{array} h1u1+h2v1+h3−h7u1u2−h8v1u2=u2h4u1+h5v1+h6−h7u1v2−h8v1v2=v2
这样一对匹配点,就可以获得两个方程,当有4对匹配点时,则可以得到如下方程组:
( u 1 1 v 1 1 1 0 0 0 − u 1 1 u 2 1 − v 1 1 u 2 1 0 0 0 u 1 1 v 1 1 1 − u 1 1 v 2 1 − v 1 1 v 2 1 u 1 2 v 1 2 1 0 0 0 − u 1 2 u 2 2 − v 1 2 u 2 2 0 0 0 u 1 2 v 1 2 1 − u 1 2 v 2 2 − v 1 2 v 2 2 u 1 3 v 1 3 1 0 0 0 − u 1 3 u 2 3 − v 1 3 u 2 3 0 0 0 u 1 3 v 1 3 1 − u 1 3 v 2 3 − v 1 3 v 2 3 u 1 4 v 1 4 1 0 0 0 − u 1 4 u 2 4 − v 1 4 u 2 4 0 0 0 u 1 4 v 1 4 1 − u 1 4 v 2 4 − v 1 4 v 2 4 ) ( h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 ) = ( u 2 1 v 2 1 u 2 2 v 2 2 u 2 3 v 2 3 u 2 4 v 2 4 ) \left(\begin{array}{cccccccc} u_{1}^{1} & v_{1}^{1} & 1 & 0 & 0 & 0 & -u_{1}^{1} u_{2}^{1} & -v_{1}^{1} u_{2}^{1} \\ 0 & 0 & 0 & u_{1}^{1} & v_{1}^{1} & 1 & -u_{1}^{1} v_{2}^{1} & -v_{1}^{1} v_{2}^{1} \\ u_{1}^{2} & v_{1}^{2} & 1 & 0 & 0 & 0 & -u_{1}^{2} u_{2}^{2} & -v_{1}^{2} u_{2}^{2} \\ 0 & 0 & 0 & u_{1}^{2} & v_{1}^{2} & 1 & -u_{1}^{2} v_{2}^{2} & -v_{1}^{2} v_{2}^{2} \\ u_{1}^{3} & v_{1}^{3} & 1 & 0 & 0 & 0 & -u_{1}^{3} u_{2}^{3} & -v_{1}^{3} u_{2}^{3} \\ 0 & 0 & 0 & u_{1}^{3} & v_{1}^{3} & 1 & -u_{1}^{3} v_{2}^{3} & -v_{1}^{3} v_{2}^{3} \\ u_{1}^{4} & v_{1}^{4} & 1 & 0 & 0 & 0 & -u_{1}^{4} u_{2}^{4} & -v_{1}^{4} u_{2}^{4} \\ 0 & 0 & 0 & u_{1}^{4} & v_{1}^{4} & 1 & -u_{1}^{4} v_{2}^{4} & -v_{1}^{4} v_{2}^{4} \end{array}\right)\left(\begin{array}{c} h_{1} \\ h_{2} \\ h_{3} \\ h_{4} \\ h_{5} \\ h_{6} \\ h_{7} \\ h_{8} \end{array}\right)=\left(\begin{array}{c} u_{2}^{1} \\ v_{2}^{1} \\ u_{2}^{2} \\ v_{2}^{2} \\ u_{2}^{3} \\ v_{2}^{3} \\ u_{2}^{4} \\ v_{2}^{4} \end{array}\right) u110u120u130u140v110v120v130v140101010100u110u120u130u140v110v120v130v1401010101−u11u21−u11v21−u12u22−u12v22−u13u23−u13v23−u14u24−u14v24−v11u21−v11v21−v12u22−v12v22−v13u23−v13v23−v14u24−v14v24 h1h2h3h4h5h6h7h8 = u21v21u22v22u23v23u24v24
求解该非齐次方程组,可以得到H矩阵的每个系数。
从单应矩阵恢复相机运动
而从H矩阵恢复相机运动,也可以通过奇异值分解的方法,即:
分解的结果会有八组解,此时会把八组解都进行验证,取重投影误差最小的一组,作为最优解。
单应矩阵在相机发生纯旋转时,仍然可以求得旋转,而不是像本质矩阵,在发生纯旋转时,方程其实是失效的,此时求得的矩阵受噪声影响很大,而单应矩阵能更好的应对这个纯旋转问题,来恢复相机的运动。
三角测量
单张图像是无法得到特征点深度的,在有两张图像后,通过本质矩阵或者单应矩阵,我们可以恢复相机之间的运动。在求得相机运动后,可以通过三角测量,来求得特征点在相机坐标系下的坐标。
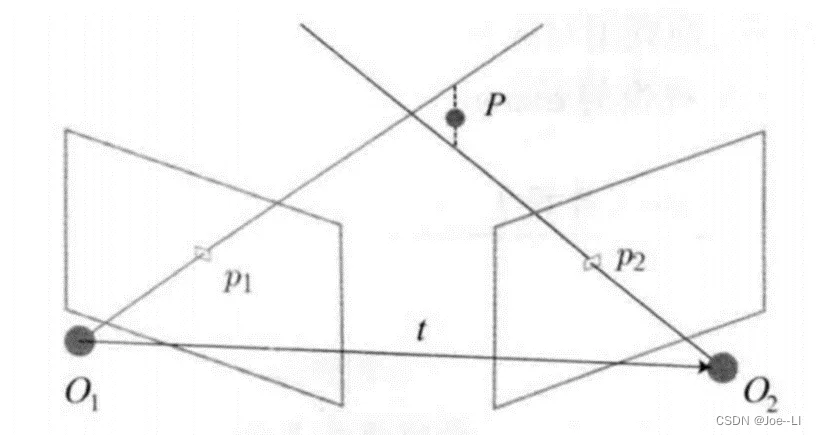
假设x1,x2是两个特征点(实际物体)的归一化坐标,那么它们满足:
s 2 x 2 = s 1 R x 1 + t s_2x_2=s_1Rx_1+t s2x2=s1Rx1+t
其中R与t为O2下O1的位姿。上式两边,同时乘以x2^,可得:
s 2 x 2 ∧ x 2 = s 1 x 2 ∧ R x 1 + x 2 ∧ t s_2x_2^\land x_2=s_1x_2^\land Rx_1+x_2^\land t s2x2∧x2=s1x2∧Rx1+x2∧t
显然左式等于0,于是有:
s 1 x 2 ∧ R x 1 + x 2 ∧ t = 0 s_1x_2^\land Rx_1+x_2^\land t=\ 0 s1x2∧Rx1+x2∧t= 0
该式中只有s1一个未知数,可以很方便得求出p1的深度。有了p1深度,p2的深度s2也很容易求出了。实际中由于噪声的存在,R,t不一定能使方程准确的等于0,更常见的做法是通过二小二乘的方式求得点的坐标,而不是直接求解。
参考链接:https://www.guyuehome.com/
相关文章:

视觉里程计之对极几何
视觉里程计之对极几何 前言 上一个章节介绍了视觉里程计关于特征点的一些内容,相信大家对视觉里程计关于特征的描述已经有了一定的认识。本章节给大家介绍视觉里程计另外一个概念,对极几何。 对极几何 对极几何是立体视觉中的几何关系,描…...
数据可视化高级技术(Echarts)
目录 (一)数据可视化概念及Echarts基础知识 数据可视化的好处: 数据可视化的目标 数据可视化的基本流程 (二)数据图表 类别比较图表: 数据关系图表: 数据分布图表: 时间序列…...
设计模式——行为型——责任链模式Chain Of Responsibility
请求类 public class ApproverRequest {private int type;//请求批准的类型private float price;//请求的金额private int id;//请求的编号 } 审批人抽象类 public abstract class ApproverPerson {protected ApproverPerson next;protected String name;//审批过程public a…...

设计模式之工厂方法模式精讲
工厂方法模式又叫虚拟构造函数(Virtual Constructor)模式或者多态性工厂(Polymorphic Factory)模式。工厂方法模式的用意是定义一个创建产品对象的工厂接口,将实际创建性工作推迟到子类中。 工厂模式可以分为简单工厂…...
)
JS实现省市区三级联动(json假数据)
省市级三级联动通常指的是在用户界面上,用户可以通过选择省份,然后基于所选择的省份选择对应的城市,最后基于所选择的城市选择对应的区县。这种联动效果在很多应用中都有出现,例如电商平台的收货地址选择、政务服务的地区选择等。…...

Fastjson配置消息转换器(时间格式问题)
问题: 我们可以看见,日期的格式有点问题。 由于ArticleListVO类的createTime成员变量是Date类型,默认是由java的Jackson来处理,使用 ISO-8601 规范来处理日期时间格式。ISO-8601 是一种国际标准的日期时间表示法,例如&…...

安卓Android 架构模式及UI布局设计
文章目录 一、Android UI 简介1.1 在手机UI设计中,坚持的原则是什么1.2 安卓中的架构模式1.2.1 MVC (Model-View-Controller)设计模式优缺点 1.2.2 MVP(Model-View-Presenter)设计模式MVP与MVC关系: 1.2.3 MVVM(Model—View—ViewModel ) 设计模式1.2.4 …...
基于Spring Boot的在线学习系统的设计与实现
基于Spring Boot的在线学习系统的设计与实现 摘 要 在线学习系统是以大学传统线下教学方式不适应信息技术的迅速发展为背景,提高学习效率,解决传统教学问题,并且高效的实现教学信息化的一款软件系统。为了更好的实现对于教学和学生的管理&a…...

C++中重载和重写的区别
重载 是指同一可访问区内被声明的几个具有不同参数列(参数的类型,个数,顺序不同)的同名函数,根据参数列表确定调用哪个函数,重载不关心函数返回类型。 #include<bits/stdc.h>using namespace std;cl…...

二叉树 - 栈 - 计数 - leetcode 331. 验证二叉树的前序序列化 | 中等难度
题目 - 点击直达 leetcode 331. 验证二叉树的前序序列化 | 中等难度1. 题目详情1. 原题链接2. 基础框架 2. 解题思路1. 题目分析2. 算法原理方法1:栈方法2:计数 3. 时间复杂度 3. 代码实现方法1:栈方法2:计数 leetcode 331. 验证二…...

Training language models to follow instructions with human feedback
Abstract 使语言模型变得更大并不意味着它们本身就能更好地遵循用户的意图。模型的输出结果可能存在以下问题 不真实有毒对用户没有帮助即这些模型没有和用户 “对齐”(aligned) 在给定的 Prompt 分布上,1.3B 的 InstructGPT 的输出比 175B GPT-3 的输出更好(尽管参数量相…...
Netty核心原理剖析与RPC实践11-15
Netty核心原理剖析与RPC实践11-15 11 另起炉灶:Netty 数据传输载体 ByteBuf 详解 在学习编解码章节的过程中,我们看到 Netty 大量使用了自己实现的 ByteBuf 工具类,ByteBuf 是 Netty 的数据容器,所有网络通信中字节流的传输都是…...
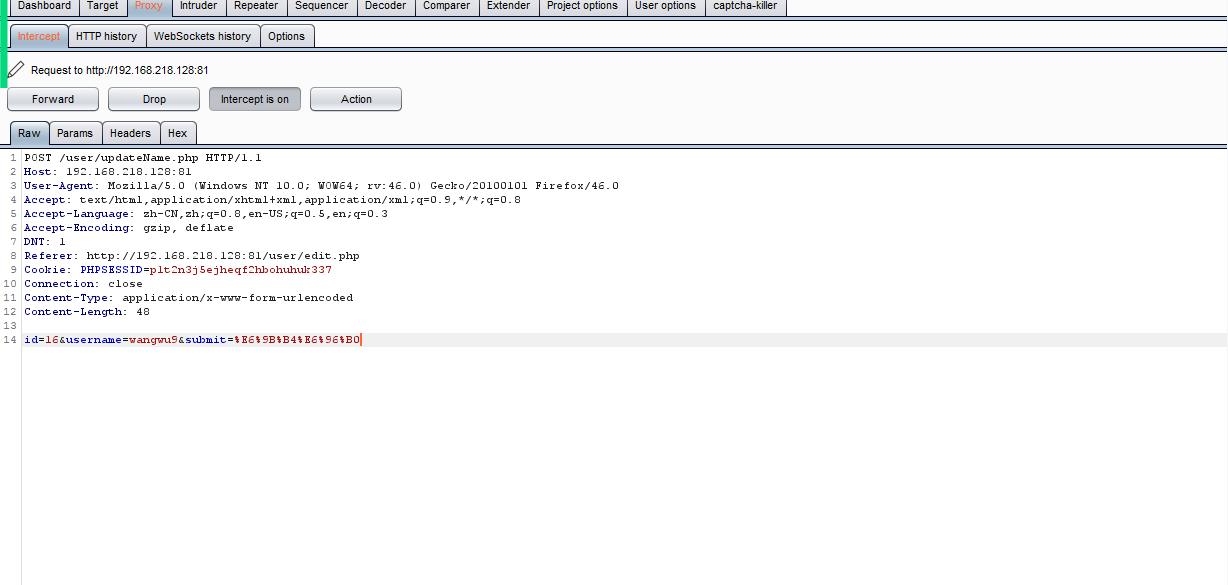
3.5网安学习第三阶段第五周回顾(个人学习记录使用)
本周重点 ①SSRF服务器端请求伪造 ②序列化和反序列化 ③Vaudit代码审计 本周主要内容 ①SSRF服务器端请求伪造 一、概述 SSRF: server site request forgery (服务器端请求伪造)。 SSR: 服务端请求,A服务器通过函数向B服务器发送请求。 SSRF发生的前提条件…...

kali常用命令功能简介记录
Kali Linux中常用的命令: 1. apt-get update:更新软件源列表。 2. apt-get upgrade:升级系统中已安装的软件包。 3. apt-get install [软件包]:安装指定的软件包。 4. apt-get remove [软件包]:卸载指定的软件包。 5.…...
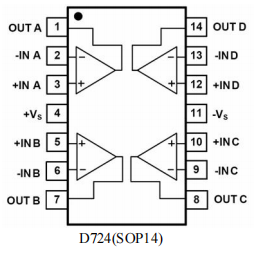
低噪声、轨至轨运算放大器芯片—— D721、D722、D724,适合用于音频领域
应用领域 D721、D722、D724是我们推荐的三款低噪声、轨至轨运算放大器芯片,其中D721为单运放,D722为双运放,D724为四运放。适合用于音频领域、传感器等的信号放大处理,比如K歌宝、音响、测距、滤波器、AD转换器前级信号处理等等。…...

【统计】什么事 R 方
将线性模型拟合到时间序列时,通常使用最小二乘法在模型 y ^ ( t ) a b t \hat{y}(t) a bt y^(t)abt中找到系数 a a a和 b b b,其中 y ^ ( t ) \hat{y}(t) y^(t)是时间 t t t的预测值,而的观测值是 y ( t ) y(t) y(t)。 残差平方和又…...

Maplesoft Maple 2024(数学科学计算)mac/win
Maplesoft Maple是一款强大的数学计算软件,提供了丰富的功能和工具,用于数学建模、符号计算、数据可视化等领域的数学分析和解决方案。 Mac版软件下载:Maplesoft Maple 2024 for mac激活版 WIn版软件下载:Maplesoft Maple 2024特别…...

实战 | YOLOv8自定义数据集训练实现手势识别 (标注+训练+预测 保姆级教程--含数据集)
导 读 本文将手把手教你用YoloV8训练自己的数据集并实现手势识别。 安装环境 【1】安装torch, torchvision对应版本,这里先下载好,直接安装 pip install torch-1.13.1+cu116-cp38-cp38-win_amd64.whlpip install torchvision-0.14.1+cu116-cp38-cp38-win_amd64.whl 安装好…...

从零学算法2810
2810.你的笔记本键盘存在故障,每当你在上面输入字符 ‘i’ 时,它会反转你所写的字符串。而输入其他字符则可以正常工作。 给你一个下标从 0 开始的字符串 s ,请你用故障键盘依次输入每个字符。 返回最终笔记本屏幕上输出的字符串。 示例 1&am…...

Vue——案例01(查询用户)
目录 一、案例实现页面 二、案例实现效果 1. 查询效果 2. 年龄升序 3. 年龄降序 4. 原顺序 三、案例实现思路 四、完整代码 一、案例实现页面 实现用户对年龄的升降的排序、根据名字搜索用户信息以及重新返回原序列 二、案例实现效果 1. 查询效果 2. 年龄升序 3. 年龄…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
