图论模板详解
目录
Floyd算法
例题:蓝桥公园
Dijkstra算法
例题:蓝桥王国
SPFA算法
例题:随机数据下的最短路问题
总结
最小生成树MST
Prim算法
Kruskal算法
例题:聪明的猴子
Floyd算法
最简单的最短路径算法,使用邻接矩阵存图,因为Floyd算法计算的结果是所有点对之间的最短路,本身就要的空间,用矩阵存储最合适。效率不高,计算复杂度为
,只能用于n<300的小规模的图,不能用于大图,在某些场景下有自己的优势,难以替代,能做传递闭包问题。
for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i][j],d[i][k]+dp[k][j]);}}
} Floyd算法是多源最短路算法,以此计算能得到图中每一对结点之间(多对多)的最短路径。
Floyd算法能判断负圈,若图中有权值为负的边,某个经过这个负边的环路,所有边长相加的总长度也是负数,这就是负圈。在这个负圈上每绕一圈,总长度就更小,从而陷入在兜圈子的死循环。Floyd算法很容易判断负圈,只要在算法运行过程中出现任意一个dp[i][j]<0就说明有负圈,因为dp[i][j]是从i出发,经过其它中转点绕一圈回到自己的最短路径,如果等于0,就存在负圈。
例题:蓝桥公园

#include<bits/stdc++.h>
using namespace std;
const long long INF=0x3f3f3f3f3f3f3f3fLL;
const int N=405;
long long dp[N][N];
int n,m,q;
void floyd(){for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]);}}}
}
int main(){cin>>n>>m>>q;memset(dp,0x3f,sizeof(dp));for(int i=1;i<=m;i++){int u,v;long long w;cin>>u>>v>>w;dp[u][v]=dp[v][u]=min(dp[u][v],w);}floyd();while(q--){int s,t;cin>>s>>t;if(dp[s][t]==INF){cout<<"-1"<<endl;}else if(s==t){cout<<"0"<<endl;}else{cout<<dp[s][t]<<endl;}}return 0;
}Dijkstra算法
Dijkstra算法用于求解单源最短路径问题,非常高效而且稳定,但是只能处理不含负权边的图。
Dijkstra算法是贪心思想实现的,首先把起点到所有点的距离存下来找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其它所有点的最短距离。
采用优先队列实现,每次往队列中放数据时,按从小到大的顺序放,采用小顶堆的方式,复杂度是,保证最小的数总在最前面。找最小值,直接取第一个数,复杂度是
。

例题:蓝桥王国

#include<bits/stdc++.h>
using namespace std;
const long long INF=0x3f3f3f3f3f3f3f3fLL;
const int N=3e5+2;
struct edge{int from,to;long long w;edge(int a,int b,long long c){from=a;to=b;w=c;}
};
vector<edge>e[N];
struct s_node{int id;long long n_dis;s_node(int b,long long c){id=b;n_dis=c;}bool operator < (const s_node &a) const{ return n_dis>a.n_dis;}
};
int n,m;
int pre[N];
void print_path(int s,int t){if(s==t){printf("%d ",s);return;}print_path(s,pre[t]);printf("%d ",t);
}
long long dis[N];
void dijkstra(){int s=1;bool done[N];for(int i=1;i<=n;i++){dis[i]=INF;done[i]=false;}dis[s]=0;priority_queue<s_node>Q;Q.push(s_node(s,dis[s]));while(!Q.empty()){s_node u=Q.top();Q.pop();if(done[u.id]){continue;}done[u.id]=true;for(int i=0;i<e[u.id].size();i++){edge y=e[u.id][i];if(done[y.to]){continue;}if(dis[y.to]>y.w+u.n_dis){dis[y.to]=y.w+u.n_dis;Q.push(s_node(y.to,dis[y.to]));pre[y.to]=u.id;}}}
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){e[i].clear();}while(m--){int u,v,w;cin>>u>>v>>w;e[u].push_back(edge(u,v,w));}dijkstra();for(int i=1;i<=n;i++){if(dis[i]>=INF){cout<<"-1";}else{cout<<dis[i];}}return 0;
}SPFA算法
SPFA算法=队列处理+Bellman-Ford
Bellman-Ford算法有很多低效或无效的操作,其核心内容,是在每一轮操作中,更新所有节点到起点s的最短距离。
计算和调整一个节点u到s的最短距离后,如果紧接着调整u的邻居节点,这些邻居肯定有新的计算结果,而如果漫无目的的计算不与u相邻的节点,这可能毫无变化,所以这些操作是低效的。
改进:计算结点u之后,下一步只计算和调整它的邻居,能加速收敛的过程。这些步骤用队列操作

例题:随机数据下的最短路问题

#include<bits/stdc++.h>
using namespace std;
const long long INF=0x3f3f3f3f3f3f3f3f;
const int N=5e3+10;
struct edge{int to;long long w;edge(int tt,long long ww){to=tt;w=ww;}
};
long long dist[N];
int inq[N];
vector<edge>e[N];
void spfa(int s){memset(dist,0x3f,sizeof(dist));dist[s]=0;queue<int>q;q.push(s);inq[s]=1;while(!q.empty()){int u=q.front();q.pop();inq[u]=0;if(dist[u]==INF){continue;}for(int i=0;i<e[u].size();i++){int v=e[u][i].to;long long w=e[u][i].w;if(dist[v]>dist[u]+w){dist[v]=dist[u]+w;if(!inq[v]){q.push(v);inq[v]=1;}}}}
}
int main(){int n,m,s;cin>>n>>m>>s;for(int i=1;i<=m;i++){int u,v;long long w;cin>>u>>v>>w;e[u].push_back(edge(v,w));}spfa(s);for(int i=1;i<=n;i++){if(dist[i]==INF){cout<<-1;}else{cout<<dist[i];}if(i!=n){cout<<" ";}else{cout<<endl;}}return 0;
}总结
单源最短路
(1)当权值非负时,用Dijkstra算法。
(2)当权值有负值,且没有负圈,则用SPFA。SPFA能检测负圈,但是不能输出负圈。
(3)当权值有负值而且有负圈需要输出,则用Bellman-Ford,能够检测并输出负圈。
多源最短路
使用Floyd算法。
最小生成树MST
一个含有n个结点的连通图的生成树是原图的极小连通子图,包含原图中的所有n个结点,并且边的权值之和最小。
Prim算法
对点进行贪心操作,从任意一个点u开始,把距离它最近的点加入到MST中,下一步,把距离{u,v}最近的点w加入到MST中;继续这个过程,直到所有的点都在MST中。适用于稠密图。
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f3f3f3f3f;
const int MAXN=1005;
vector<int>demo;
int closest[MAXN],lowcost[MAXN],n,m;//m为节点的个数,n为边的数量
int G[MAXN][MAXN];//邻接矩阵
int prim(){for(int i=0;i<n;i++){lowcost[i]=INF;}for(int i=0;i<m;i++){closest[i]=0;}closest[0]=-1;//加入第一个点,-1表示该点在集合U中,否则在集合V中int num=0,ans=0,e=0;while(num<m-1){//当点还没有全部放进去 int micost=INF;for(int i=0;i<m;i++){if(closest[i]!=-1){int temp=G[e][i];if(temp<lowcost[i]){lowcost[i]=temp;closest[i]=e;}if(lowcost[i]<micost){micost=lowcost[i];}}ans+=micost;demo.push_back(micost);closest[e]=-1;num++;}} return ans;
}
int main(){cin>>m>>n;memset(G,INF,sizeof(G));for(int i=0;i<n;i++){int a,b,c;cin>>a>>b>>c;G[b][a]=G[a][b]=c;}cout<<prim()<<endl;for(int i=0;i<m-1;i++){cout<<demo[i]<<" ";}return 0;
}Kruskal算法
对边进行贪心操作。从最短的边开始,把它加入到MST中,在剩下的边中找最短的边,加入到 MST中,继续这个过程,直到所有的点都在MST中。适用于稀疏图。
kruskal算法的两个关键技术:
(1)对边进行排序
(2)判断圈,即处理连通性问题。这个问题用并查集简单而高效,并查集是krustral算法的绝配。
例题:聪明的猴子


#include<bits/stdc++.h>
using namespace std;
int n,m,father[1100000];
struct node{int x,y,k;
}Q[1100000];
int find(int x){if(father[x]==x){return x;}return father[x]=find(father[x]);
}
bool cmp(node a,node b){return a.k<b.k;
}
int main(){cin>>n>>m;int sum=0,st=0;for(int i=0;i<m;i++){//把m条边扫描进来 cin>>Q[i].x>>Q[i].y>>Q[i].k;}sort(Q,Q+m,cmp);for(int i=1;i<=n;i++){father[i]=i;}for(int i=0;i<m;i++){int tx=find(Q[i].x);int ty=find(Q[i].y);if(tx!=ty){sum+=Q[i].k;st++;father[tx]=ty;if(st==n-1){break;}}}cout<<sum<<endl;return 0;
}相关文章:

图论模板详解
目录 Floyd算法 例题:蓝桥公园 Dijkstra算法 例题:蓝桥王国 SPFA算法 例题:随机数据下的最短路问题 总结 最小生成树MST Prim算法 Kruskal算法 例题:聪明的猴子 Floyd算法 最简单的最短路径算法,使用邻接…...
ArcGIS Pro打不开Excel?Microsoft驱动程序安装不上?
刚用ArcGIS pro的朋友们可能经常在打开xls或者xlsx文件的时候都会提示,未安装所需的Microsoft驱动程序。 怎么办呢?当然,按照提示装一下驱动就会好吗?有什么状况会出现?有什么临时替代方案呢? 全文目录&a…...

简单了解裸眼3D呈现技术
裸眼3D呈现是一种不需要佩戴任何特殊设备(如3D眼镜或头盔)即可观看到3D效果的技术。这种技术近年来得到了快速发展,为观众带来了更加沉浸式的视觉体验。 实现裸眼3D呈现的关键步骤包括: 创建立体图像源:首先需要有一…...

单元测试——Junit (断言、常用注解)
单元测试 Junit单元测试框架 使用 断言测试 使用Assert.assertEquals(message, 预期值, 实际值); 这段代码是用于在测试中验证某个方法的返回值是否符合预期。其中,"方法内部有bug"是用于在断言失败时显示的提示信息。4是预期的返回值,index…...

【蓝桥杯每日一题】4.2 全球变暖
原题链接:1233. 全球变暖 - AcWing题库 由题意可知: 需要找到淹没的岛屿的数量淹没的岛屿所具备的条件:咩有“高地”,也就是说岛屿(连通块)中的所有元素的 4 4 4-邻域中均含有’ . ’ 思路1:…...

ffmpeg点对点音视频udp协议传输
参考:https://zhuanlan.zhihu.com/p/636152437?utm_id0 ffmpeg查看可用设备: ffmpeg -list_devices true -f dshow -i dummy1、音频 局域网内两台设备间 设备1-音频: ffmpeg -f dshow -i audio"麦克风阵列 (适用于数字麦克风的英特…...
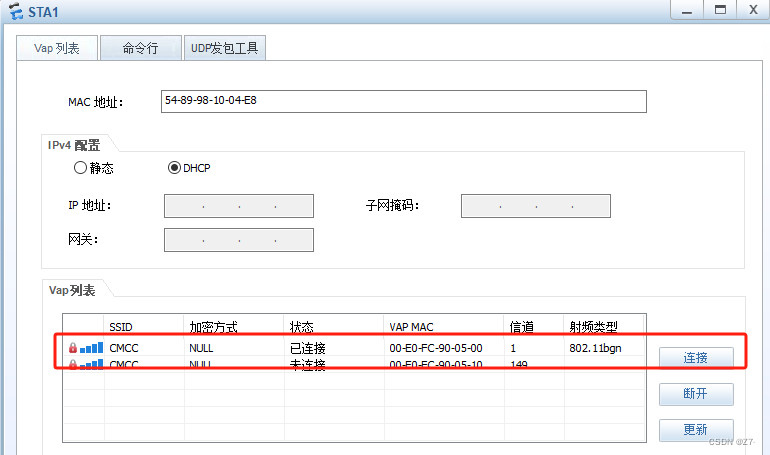
ensp华为AC+AP上线配置
AR1配置: <Huawei>system-view # 进入系统视图<Huawei>sysname R1 # 设备重命名[R1]dhcp enable # 开启DHCP功能[R1]interface GigabitEthernet0/0/0 # 进入接口 [R1-GigabitEthernet0/0/0]ip address 192.168.0.1 23 # 配置接口地址 [R1-GigabitE…...

JAVA基础02-Java语言基础以及编译准备工作
什么是JAVA语言 Java是一门面向对象的编程语言,不仅吸收了C语言的各种优点,还摒弃了C里难以理解的多继承、指针等概念,因此Java语言具有功能强大和简单易用的两个特征。 (可以编写桌面应用程序、Web应用程序、分布式系统和嵌入式…...

Photoshop 2024 Mac/win---图像处理的新纪元,解锁无限创意
Photoshop 2024是一款功能强大的图像处理软件,以其卓越的性能和广泛的应用领域,赢得了设计师、摄影师、图形艺术家等各类创意工作者的青睐。它提供了丰富的绘画和编辑工具,让用户能够轻松进行图片编辑、合成、校色、抠图等操作,实…...

【MySQL系列】使用 ALTER TABLE 语句修改表结构的方法
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

ElementUI 表格横向滚动条时滚动到指定位置
ElementUI 表格横向滚动条时滚动到指定位置 getColumnOffset(columnProp) {this.$nextTick(() > {const table this.$refs.tableRef.$refs.multipleTable;const columns table.columns;const column columns.find((col) > col.property columnProp);if (column) {// …...
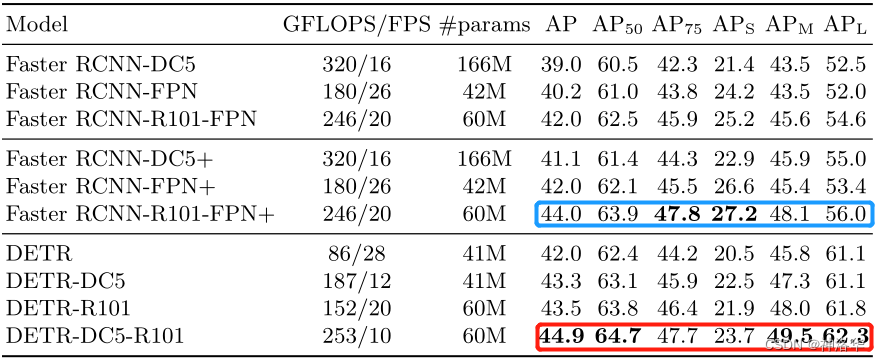
【论文阅读】DETR 论文逐段精读
【论文阅读】DETR 论文逐段精读 文章目录 【论文阅读】DETR 论文逐段精读📖DETR 论文精读【论文精读】🌐前言📋摘要📚引言🧬相关工作🔍方法💡目标函数📜模型结构⚙️代码 Ǵ…...

负载均衡:实现高效稳定的网络服务
随着互联网技术的快速发展,网络应用服务的规模和复杂性日益增加。为了满足日益增长的用户需求,确保服务的高可用性和稳定性,负载均衡技术应运而生。本文将详细介绍负载均衡的概念、原理、分类以及应用场景,帮助读者深入了解这一关…...

2024最新软件测试【测试理论+ 抓包与网络协议】面试题(内附答案)
一、测试理论 3.1 你们原来项目的测试流程是怎么样的? 我们的测试流程主要有三个阶段:需求了解分析、测试准备、测试执行。 1、需求了解分析阶段 我们的 SE 会把需求文档给我们自己先去了解一到两天这样,之后我们会有一个需求澄清会议, …...

极简7照训练法,奇趣相机引领儿童AI摄影潮流
近日,奇趣未来推出一款专注于儿童AI摄影市场的微信小程序——奇趣相机,搭载了专为中国儿童精心研发的AIGC大模型,精准捕捉并贴合亚洲儿童人脸特征,让每一个孩子的笑容都能被完美定格。它不仅涵盖了从3岁至12岁各个年龄段的儿童摄影…...

Flink应用
1.免密登录 2.flink StandAlone模式 3.Flink Yarn 模式 (on per 模式,on session 模式) Flink概述 按照Apache官方的介绍,Flink是一个对有界和无界数据流进行状态计算的分布式处理引擎和框架。通俗地讲,Flink就是一个流计算框架,主要用来处…...

C# 委托与事件 终章
C# 委托与事件 浅尝 C# 委托与事件 深入 委托 委托有什么用? 将函数作为函数的参数传递声明事件并用来注册 强类型委托 Action<T1> Func<T1, TResult>事件 希望一个类的某些成员在发生变化时能被外界观测到 CollctionChangedTextChanged 标准.Ne…...

MySQL-linux安装-万能RPM法
一、MySQL的Linux版安装 1、 CentOS7下检查MySQL依赖 1. 检查/tmp临时目录权限(必不可少) 由于mysql安装过程中,会通过mysql用户在/tmp目录下新建tmp_db文件,所以请给/tmp较大的权限。执行 : chmod -R 777 /tmp2. …...

elment UI el-date-picker 月份组件选定后提交后台页面显示正常,提交后台字段变成时区格式
需求:要实现一个日期的月份选择<el-date-picker :typeformData.dateType :value-formatdateFormat v-modelformData.leaveFactoryDateplaceholder选择月份></el-date-picker>错误示例:将日期显示类型(type)dateType或将日期绑定值的格式(val…...

基于 NGINX 的 ngx_http_geoip2 模块 来禁止国外 IP 访问网站
基于 NGINX 的 ngx_http_geoip2 模块 来禁止国外 IP 访问网站 一、安装 geoip2 扩展依赖 [rootfxkj ~]# yum install libmaxminddb-devel -y二、下载 ngx_http_geoip2_module 模块 [rootfxkj tmp]# git clone https://github.com/leev/ngx_http_geoip2_module.git三、解压模…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...
