当前位置： 首页 > news >正文

VSCode美化

news 2026/2/8 1:56:21

今天有空收拾了一下VSCode，页面如下，个人觉得还是挺好看的~~
在这里插入图片描述

1. 主题

Noctis
色彩较多，有种繁杂美。
在这里插入图片描述
我使用的是浅色主题的一款Noctis Hibernus
在这里插入图片描述

2. 字体

Maple Mono
官网：Maple-Font
我只安装了下图两个字体，使用的是
在这里插入图片描述

2.1 VSCode设置字体

在这里插入图片描述

3. 背景

background
在这里插入图片描述

3.1 VSCode设置背景图

在这里插入图片描述

4. 彩虹缩进

indent-rainbow
在这里插入图片描述

5. 文件图标

Material Icon Theme
在这里插入图片描述

相关文章：

VSCode美化

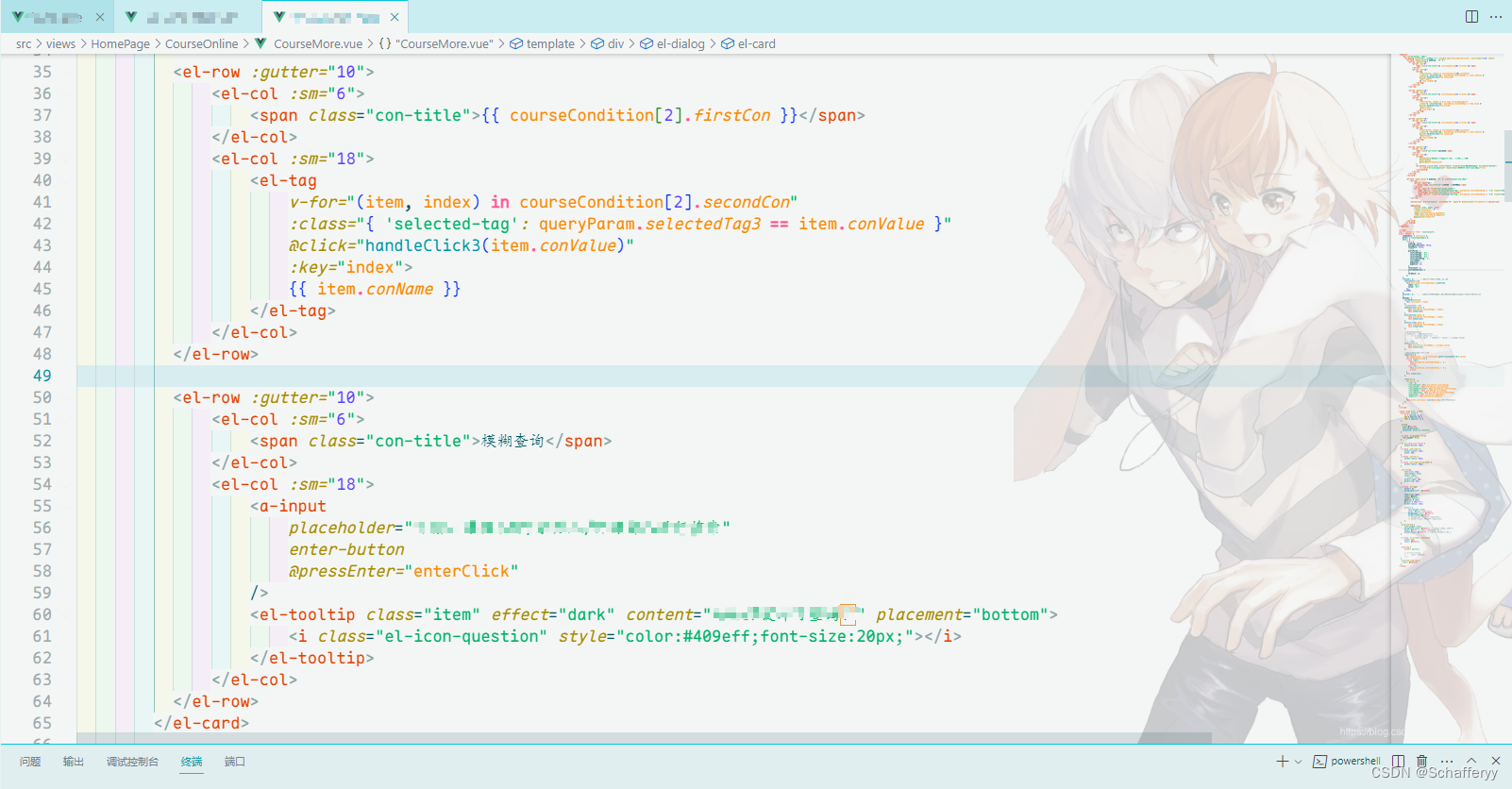
今天有空收拾了一下VSCode，页面如下，个人觉得还是挺好看的~~ 1. 主题 Noctis 色彩较多，有种繁杂美。 我使用的是浅色主题的一款Noctis Hibernus 2. 字体 Maple Mono 官网：Maple-Font 我只安装了下图两个字体，使…...

编程日记 2024/4/3 6:57:54

Runes 生态一周要览 ▣ 2024.3.25-3.31｜Runes 协议更新 BTC 减半在即

Runes 生态大事摘要 1、Casey 发布了 Runes 协议文档 RUNES HAVE DOCS，Github 代码库更新到 ord 0.17.0 版本，Casey 表示符文是一个“严肃”的代币协议。 2、Casey 公布了第一个硬编码的创世符文「UNCOMMONGOODS」 3、4月7日香港沙龙｜聚焦「…...

编程日记 2024/4/3 6:55:52

瘦身Spring Boot应用(thinJar)

瘦身Spring Boot应用(thinJar) 简介 我们使用Spring Boot提供的spring-boot-maven-plugin打包Spring Boot应用，可以直接获得一个完整的可运行的jar包，把它上传到服务器上再运行就极其方便。 但是这种方式也不是没有缺点。最大的缺点就是包太大了&…...

编程日记 2024/4/3 6:54:51

备战蓝桥杯---贪心刷题1

话不多说&#xff0c;直接看题&#xff1a; 本质是一个数学题&#xff1a; 我们令xi<0表示反方向传递&#xff0c;易得我们就是求每一个xi的绝对值之和min,我们令平均值为a爸。 易得约束条件&#xff1a; x1-x2a1-a,x2-x3a2-a..... 解得x1x1-0,x2x1-((n-1)*a-a2-...an)。…...

编程日记 2024/4/3 6:52:49

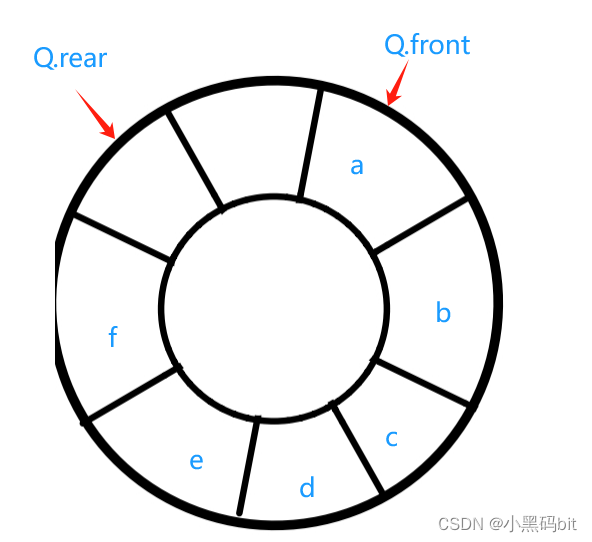
《数据结构学习笔记---第九篇》---循环队列的实现

文章目录 1.循环队列的定义 2.循环队列的判空判满 3.创建队列并初始化 4.入队和出队 5. 返回队尾队首元素 6.释放循环队列 1.循环队列的定义 定义&#xff1a;存储队列元素的表从逻辑上被视为一个环。 我们此次实现的循环队列&#xff0c;采用顺序表 typedef struct {int…...

编程日记 2024/4/3 6:49:46

前端调试工具之Chrome Elements、Network、Sources、TimeLine调试

常用的调试工具有Chrome浏览器的调试工具&#xff0c;火狐浏览器的Firebug插件调试工具&#xff0c;IE的开发人员工具等。它们的功能与使用方法大致相似。Chrome浏览器简洁快速&#xff0c;功能强大这里主要介绍Chrome浏览器的调试工具。 打开 Google Chrome 浏览器&#xff0c…...

编程日记 2024/4/3 6:43:41

vue 加 websocket 聊天

<template><div style="height: 100%; width: 100%; background-color: #fff"><div class="wrap"><!-- 头部 --><div class="titleBox"><imgsrc="@/assets/image/avatar.png"style="argin: 10p…...

编程日记 2024/4/3 6:42:40

uniapp通过蓝牙传输数据 （ios）

在uni-app中&#xff0c;可以通过uni-ble&#xff08;uni-app官方提供的蓝牙插件&#xff09;来实现iOS设备上的蓝牙数据传输。 首先&#xff0c;确保已在uni-app的manifest.json文件中添加uni-ble插件的配置&#xff1a; "permission": { "scope.userLocati…...

编程日记 2024/4/3 6:41:39

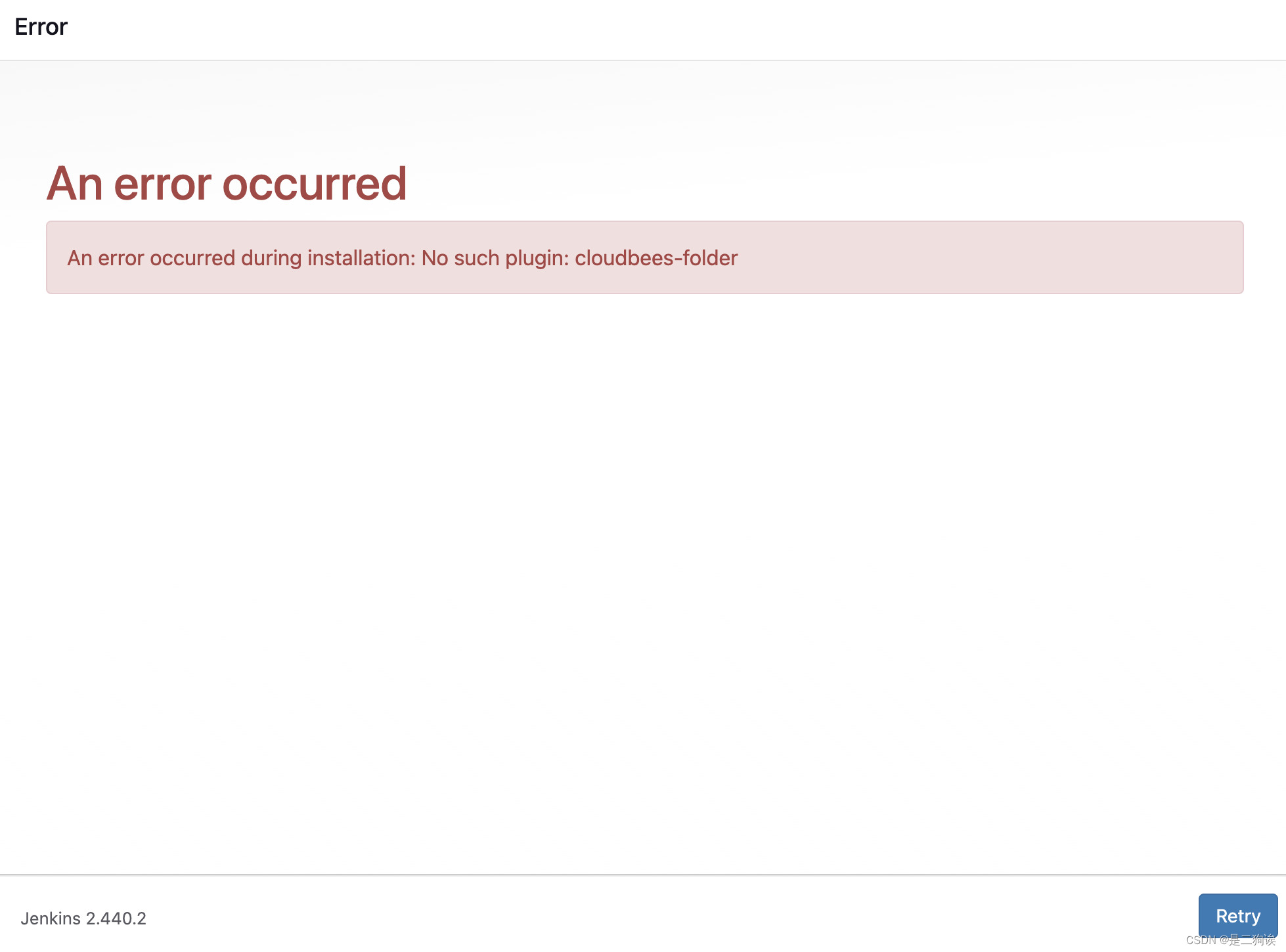
docker搭建CI/CD环境配置过程中的常见问题

一、Jenkins 1、pull镜像问题 docker pull jenkins/jenkins:lts Using default tag: latest Trying to pull repository docker.io/library/centos ... Get https://registry-1.docker.io/v2/library/centos/manifests/latest: Get https://auth.docker.io/token?scoperepo…...

编程日记 2024/4/3 6:40:38

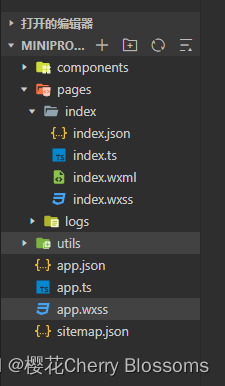
实验四 微信小程序智能手机互联网程序设计（微信程序方向）实验报告

请编写一个用户登录界面&#xff0c;提示输入用户名和密码进行登录&#xff1b; 代码 index.wxml <view class"user"> <form bindreset""> <view>用户名&#xff1a;</view><input type"text"name""/>…...

编程日记 2024/4/3 6:39:36

WPF —— 关键帧动画

wpf动画类型 1<类型>Animation这些动画称为from/to/by动画或者叫基本动画&#xff0c;他们会在起始值或者结束值进行动画处理&#xff0c;常用的例如 <DoubleAnimation> 2 <类型>AnimationUsingKeyFrames: 关键帧动画&#xff0c;功能要比from/to这些动画功…...

编程日记 2024/4/3 6:38:36

Taro + vue3 小程序封装标题组件

分为没有跳转页面的title组件和 有跳转页面的title组件 我们可以把这个封装成一个组件 直接上代码 <template><div class"fixed-title-container"><div class"box"><div class"icon" v-if"isShow" click"…...

编程日记 2024/4/3 6:37:29

babyAGI(6)-babyCoder源码阅读2任务描述部分

废话不多说&#xff0c;我们直接看task的prompt 这里需要注意的是&#xff0c;每个openai_call的temperature都不相同&#xff0c;这也是开发程序时需要调整和关注的一点 1. 初始化代码任务agent 作为babycoder的第一个angent&#xff0c;整个prompt编写的十分值得学习 整个p…...

编程日记 2024/4/3 6:35:27

生成式语言模型预训练阶段验证方式与微调阶段验证方式

生成式语言模型&#xff0c;如GPT-3、BERT等&#xff0c;在预训练和微调阶段都需要进行验证以确保模型性能。下面分别介绍这两个阶段的验证方式&#xff1a; 预训练阶段的验证&#xff1a; 预训练阶段通常使用大量未标注的文本数据来训练模型&#xff0c;以学习语言的一般特性。…...

编程日记 2024/4/3 6:33:25

flink on yarn

前言 Apache Flink&#xff0c;作为大数据处理领域的璀璨明星&#xff0c;以其独特的流处理和批处理一体化模型&#xff0c;成为众多企业和开发者的首选。它不仅能够在处理无界数据流时展现出卓越的实时性能&#xff0c;还能在有界数据批处理上达到高效稳定的效果。本文将简要…...

编程日记 2024/4/3 6:32:24

用TOMCAT部署web项目教程

文章目录 引言I 使用webapps文件夹II 利用server.xmlIII 自定义配置文件IV 预备知识4.1项目的一般结构4.2 contex标签4.3 IDE部署4.4 配置Tomcat服务引言 在开发阶段，一般使用IDE如MyEclipse来部署web项目，不要忘记手动部署的三种方式。 I 使用webapps文件夹 将项目文件夹…...

编程日记 2024/4/3 6:31:23

bash例子-source进程替换、alias不生效处理

#1. source 例子&#xff0c; 进程替换source <(echo alias zls"ls") #上一行 中 echo替换为cat&#xff0c;则得到如下行, 好处是 cat不用处理引号转义问题&#xff0c;而echo则必须处理引号转义问题#写一段复杂脚本&#xff0c;且 不处理引号转义问题 &#x…...

编程日记 2024/4/3 6:30:22

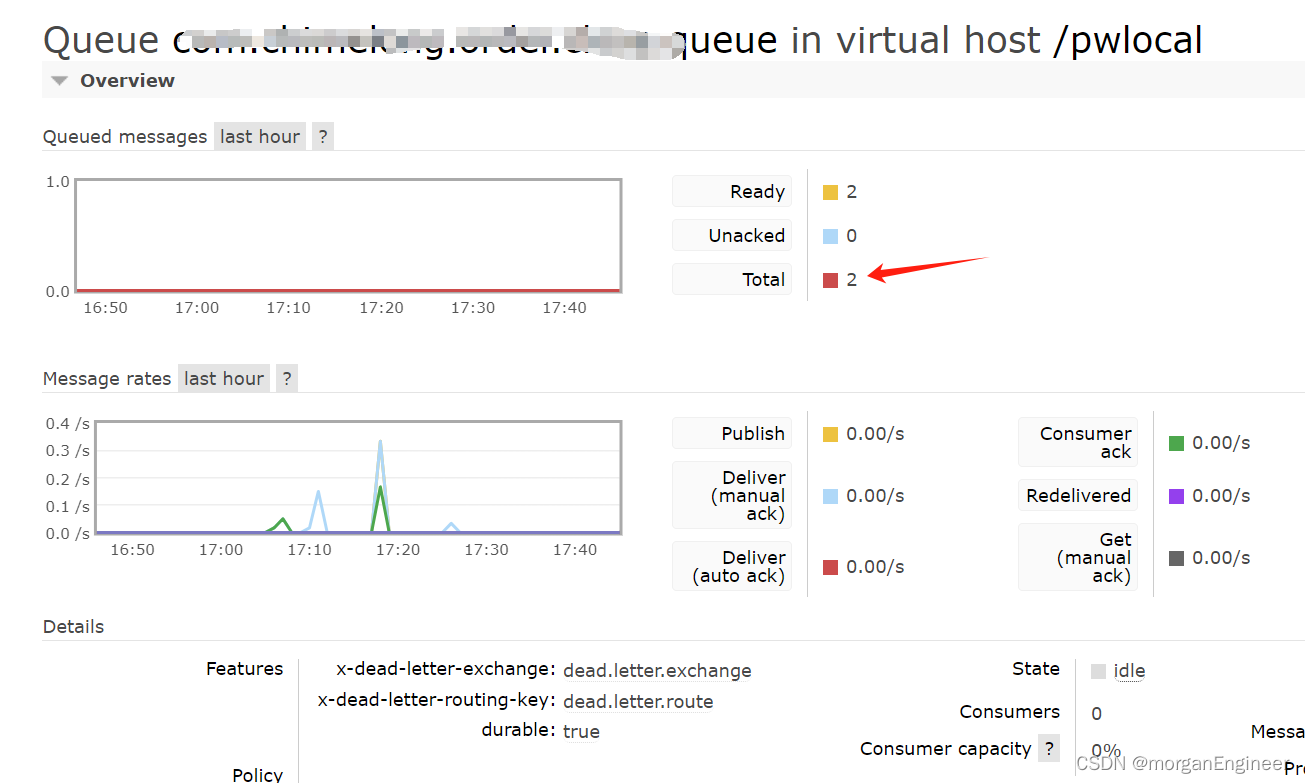
rabbitmq死信交换机，死信队列使用

背景 对于核心业务需要保证消息必须正常消费&#xff0c;就必须考虑消费失败的场景&#xff0c;rabbitmq提供了以下三种消费失败处理机制 直接reject&#xff0c;丢弃消息&#xff08;默认&#xff09;返回nack&#xff0c;消息重新入队列将失败消息投递到指定的交换机 对于核…...

编程日记 2024/4/3 6:29:21

gitlab备份与恢复

1.1.1 查看系统版本和软件版本 cat /etc/debian_version cat /opt/gitlab/embedded/service/gitlab-rails/VERSION 1.1.2 数据备份 打开/etc/gitlab/gitlab.rb配置文件&#xff0c;查看一个和备份相关的配置项 sudo vim /etc/gitlab/gitlab.rb gitlab_rails[backup_path] &q…...

编程日记 2024/4/3 6:26:18

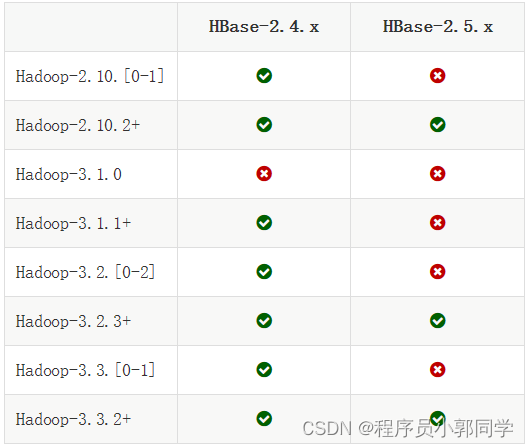
HBase详解（1）

HBase 简介 概述 HBase是Yahoo!公司开发的后来贡献给了Apache的一套开源的、分布式的、可扩展的、基于Hadoop的非关系型数据库(Non-Relational Database)&#xff0c;因此HBase并不支持SQL(几乎所有的非关系型数据库都不支持SQL)&#xff0c;而是提供了一套单独的命令和API操…...

编程日记 2024/4/3 6:25:17

手游刚开服就被攻击怎么办？如何防御DDoS？

开服初期是手游最脆弱的阶段&#xff0c;极易成为DDoS攻击的目标。一旦遭遇攻击&#xff0c;可能导致服务器瘫痪、玩家流失&#xff0c;甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案&#xff0c;帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

编程新知 2026/1/31 18:36:21

Java 语言特性(面试系列2)

一、SQL 基础 1. 复杂查询 &#xff08;1&#xff09;连接查询&#xff08;JOIN&#xff09; 内连接&#xff08;INNER JOIN&#xff09;&#xff1a;返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

编程新知 2025/10/24 14:20:29

多模态2025：技术路线“神仙打架”，视频生成冲上云霄

文&#xff5c;魏琳华 编&#xff5c;王一粟 一场大会&#xff0c;聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中&#xff0c;汇集了学界、创业公司和大厂等三方的热门选手&#xff0c;关于多模态的集中讨论达到了前所未有的热度。其中&#xff0c;…...

编程新知 2026/2/1 10:59:33

.Net框架，除了EF还有很多很多......

文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

编程新知 2026/2/1 19:26:16

基于服务器使用 apt 安装、配置 Nginx

&#x1f9fe; 一、查看可安装的 Nginx 版本 首先&#xff0c;你可以运行以下命令查看可用版本&#xff1a; apt-cache madison nginx-core输出示例&#xff1a; nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

编程新知 2026/1/9 12:53:59

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?

论文网址&#xff1a;pdf 英文是纯手打的&#xff01;论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误&#xff0c;若有发现欢迎评论指正&#xff01;文章偏向于笔记&#xff0c;谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

编程新知 2026/2/6 14:42:11

C++中string流知识详解和示例

一、概览与类体系 C 提供三种基于内存字符串的流&#xff0c;定义在 <sstream> 中&#xff1a; std::istringstream&#xff1a;输入流&#xff0c;从已有字符串中读取并解析。std::ostringstream&#xff1a;输出流&#xff0c;向内部缓冲区写入内容&#xff0c;最终取…...

编程新知 2025/11/30 11:30:47

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/12/31 6:28:08

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/2/6 1:00:25

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00