【面试经典150 | 动态规划】最小路径和
文章目录
- 写在前面
- Tag
- 题目来源
- 解题思路
- 方法一:动态规划
- 方法二:空间优化
- 写在最后
写在前面
本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更……
专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等内容进行回顾与总结,文章结构大致如下,部分内容会有增删:
- Tag:介绍本题牵涉到的知识点、数据结构;
- 题目来源:贴上题目的链接,方便大家查找题目并完成练习;
- 题目解读:复述题目(确保自己真的理解题目意思),并强调一些题目重点信息;
- 解题思路:介绍一些解题思路,每种解题思路包括思路讲解、实现代码以及复杂度分析;
- 知识回忆:针对今天介绍的题目中的重点内容、数据结构进行回顾总结。
Tag
【动态规划-空间优化】【数组】
题目来源
64. 最小路径和

解题思路
方法一:动态规划
定义状态
朴素的动态规划方法是定义状态 dp[i][j],表示从网格左上角 (0, 0) 位置到 (i, j) 位置的最小路径和。
状态转移
根据题目中 “每次只能向下或者向右移动一步”,可知到达位置 (i, j) 只能从 (i-1, j) 向下移动一步或者从 (i, j-1) 向右一步,因此有转移关系:
d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) , i ≥ 1 , j ≥ 1 dp[i][j] = min(dp[i-1][j], dp[i][j-1]), i \ge 1, j \ge 1 dp[i][j]=min(dp[i−1][j],dp[i][j−1]),i≥1,j≥1
base case
dp[0][0] = grid[0][0]。
对于网格 grid 中的第一行和第一列位置,只能从对应位置的左侧和上方的位置移动一步得到,于是需要进行如下方式的初始化:
// 第一列
for (int i = 1; i < m; ++i)dp[i][0] = dp[i - 1][0] + grid[i][0];// 第一行
for (int j = 1; j < n; ++j) {dp[0][j] = dp[0][j - 1] + grid[0][j];
}
最后返回
dp[m-1][n-1] 表示从网格左上角到网格右下角的最小路径和。
实现代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp = vector<vector<int>>(m, vector<int>(n));dp[0][0] = grid[0][0];// 对于在第一行或者第一列第一列for (int i = 1; i < m; ++i)dp[i][0] = dp[i - 1][0] + grid[i][0];第一行for (int j = 1; j < n; ++j) {dp[0][j] = dp[0][j - 1] + grid[0][j];}// 对于不在第一行和第一列的元素for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1];}
};
复杂度分析
时间复杂度: O ( m n ) O(mn) O(mn), m m m 为网格 grid 的行数, n n n 为网格的列数。
空间复杂度: O ( m n ) O(mn) O(mn)。
方法二:空间优化
方法一中朴素解法的空间复杂度可以进行优化,只需要使用 O ( m i n { m , n } ) O(min\{m, n\}) O(min{m,n}) 的复杂度即可解决。
我们以 示例 1 为例说明,如何使用线性空间解决本题。
网格的行数和列数一样,选择按行来更新最小路径和(选择列也可以),维护一个数组 dp 长度为 3。
初始化 dp = {1, 4, 5},dp[0] 表示从位置 (0, 0) 到位置 (0, 0) 的最小路径和;dp[1] 表示从位置 (0, 0) 到位置 (0, 1) 的最小路径和;dp[2] 表示从位置 (0, 0) 到位置 (0, 2) 的最小路径和。
在网格的第一行(从 0 开始数),dp[0] 表示从位置 (0, 0) 到位置 (1, 0) 的最小路径和,因为只能从 (0, 0) 位置到 (1, 0) 位置,所以更新 dp[0] = dp[0] + grid[1][0];dp[1] 表示从位置 (0, 0) 到位置 (1, 1) 的最小路径和,因为可以从 (1, 0) 位置向右或者 (0, 1) 位置向下移动到位置 (1, 1),所以有 dp[1] = min(dp[0], dp[1]) + grid[i][j]…
具体实现见如下代码。
实现代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int m = grid.size();int n = grid[0].size();int more = max(m, n);int less = min(m, n);bool rowMore = more == m; // 判断是否是行数大于等于列数vector<int> arr(less); // 以较短维度的长度作为临时空间,比如列数较小int i, j;for (i = 0; i < less; ++i) {// 更新第 0 行的所有列,即初始化if (i == 0) {arr[i] = grid[0][0];}else {arr[i] = arr[i - 1] + (rowMore ? grid[0][i] : grid[i][0]);}}for (i = 1; i < more; ++i) {// 按照行进行更新arr[0] = arr[0] + (rowMore ? grid[i][0] : grid[0][i]); // 更新 i 行 0 列的答案for (j = 1; j < less; ++j) { // 更新 i 行其他列的答案arr[j] = min(arr[j - 1], arr[j]) + (rowMore ? grid[i][j] : grid[j][i]);}}return arr[less-1];}
};
复杂度分析
时间复杂度: O ( m n ) O(mn) O(mn), m m m 为网格 grid 的行数, n n n 为网格的列数。
空间复杂度: O ( m i n { m , n } ) O(min\{m, n\}) O(min{m,n})。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【面试经典150 | 动态规划】最小路径和
文章目录 写在前面Tag题目来源解题思路方法一:动态规划方法二:空间优化 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题…...

生成式AI的情感实验——AI能否产生思想和情感?
机器人能感受到爱吗?这是一个很好的问题,也是困扰了科学家们很多年的科学未解之谜。虽然我们尚未准备好向智能机器赋予情感,但智能机器却已经可以借助生成式人工智能(AI)来帮助我们表达自己的情感。 自然情感表达 AI正…...

力扣贪心算法--第一天
前言 今天是贪心算法的第一天,算法之路重新开始! 内容 之前没了解过贪心算法。 什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。难点就是如何通过局部最优,推出整体最优。 一、455.分发饼干 假设你是一…...
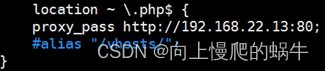
Nginx反向代理和缓存
一、Nginx反向代理 1.调度和代理的区别: 1.调度基于内核层面,代理基于应用层面 2.代理必须实现一手托两家 3.调度不需要监听任何端口,不需要工作任何应用程序,代理需要工作和上游服务器一模一样的进程 4.调度没有并发上限&am…...

支持多元AI场景应用,宁畅“NEX AI Lab”开放试用预约中
3月29日,宁畅在京举行发布会,正式发布“全局智算”战略,并在会上推出战略性新品“AI算力栈”,旨在有效解决大模型产业落地的全周期问题。 据宁畅CTO赵雷介绍,“AI算力栈”集成了宁畅在AI计算领域的软硬件能力ÿ…...

Git 如何合并多个连续的提交
我平常的编程喜欢是写一段代码就提交一次,本地一般不攒代码,生怕本地有什么闪失导致白干。但这样就又导致一个问题:查看历史日志时十分不方便,随便找一段提交可以看到: > git log --oneline 8f06be5 add 12/qemu-h…...

k8s 基础入门
1.namespace k8s中的namespace和docker中namespace是两码事,可以理解为k8s中的namespace是为了多租户,dockers中的namespace是为了网络、资源等隔离 2.deployment kubectl create #新建 kubectl aply #新建 更新 升级: 滚动升级&#x…...
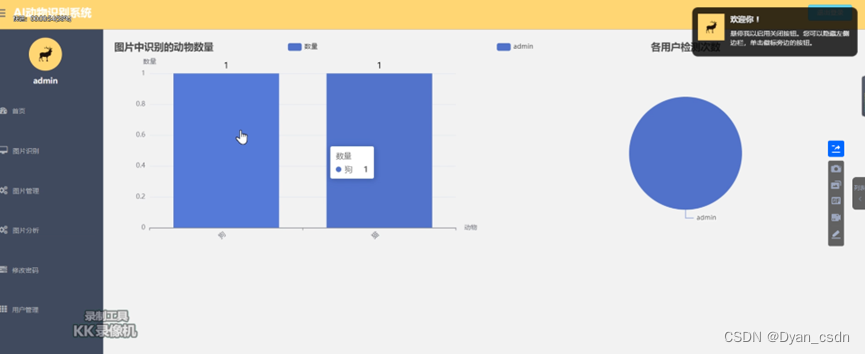
【Python项目】AI动物识别工具
目录 背景 技术简介 系统简介 界面预览 背景 成像技术在全球科技发展中扮演了关键角色。在科学研究领域,拍摄所得的图像成为了一种不可或缺的研究工具。特别是在生态学与动物学研究中,鉴于地球的广阔地域和多样的气候条件,利用图像技术捕…...
详解)
逻辑回归(Logistic Regression)详解
逻辑回归是一种用于解决二分类问题的统计方法,它通过构建一个模型来预测某个事件的概率。 以下是逻辑回归的一些关键要点: 适用场景:逻辑回归特别适合于处理二分类问题,即两个类别的分类问题,例如判断一封邮件是否为…...

.vimrc文件的语句语法
本文结构: a、简介 b、详细解释其中的一些常见语句和语法。 a、.vimrc 文件是 Vim 编辑器用于配置用户设置和自定义行为的文件。当 Vim 启动时,它会读取 .vimrc 文件中的命令和设置,并根据这些指令来配置编辑器的行为。 b、.vimrc 文件中…...

c语言之函数指针作形参
在一些c语言的大工程中,会在定义的函数中,把一些其他函数指针作为本函数形参。 函数指针作形参的例子 代码如下: #include<stdio.h> int max(int a,int b) { return(a>b?a:b); } int min(int a,int b) { return(a<b?a:b); } i…...

python文件的读取操作
打开文件 fopen("F:/python/helloworld/测试.txt","r",encoding"UTF-8")读取文件 print(f"读取10个字节的结果{f.read(10)}") print(f"读取全部字节的结果{f.read()}") linesf.readlines() print(f"{lines}")读…...

查看并设定【网络适配器】的优先级(跃点数)
目录 前言: 1.查看所有的适配器 2.修改优先级(需要以管理员身份运行) 跃点数(InterfaceMetric ) DHCP 3.修改后的效果 pwoerShell 再次运行之前的程序 4.其他 参考 网络适配器1,8相关知识介绍1 …...
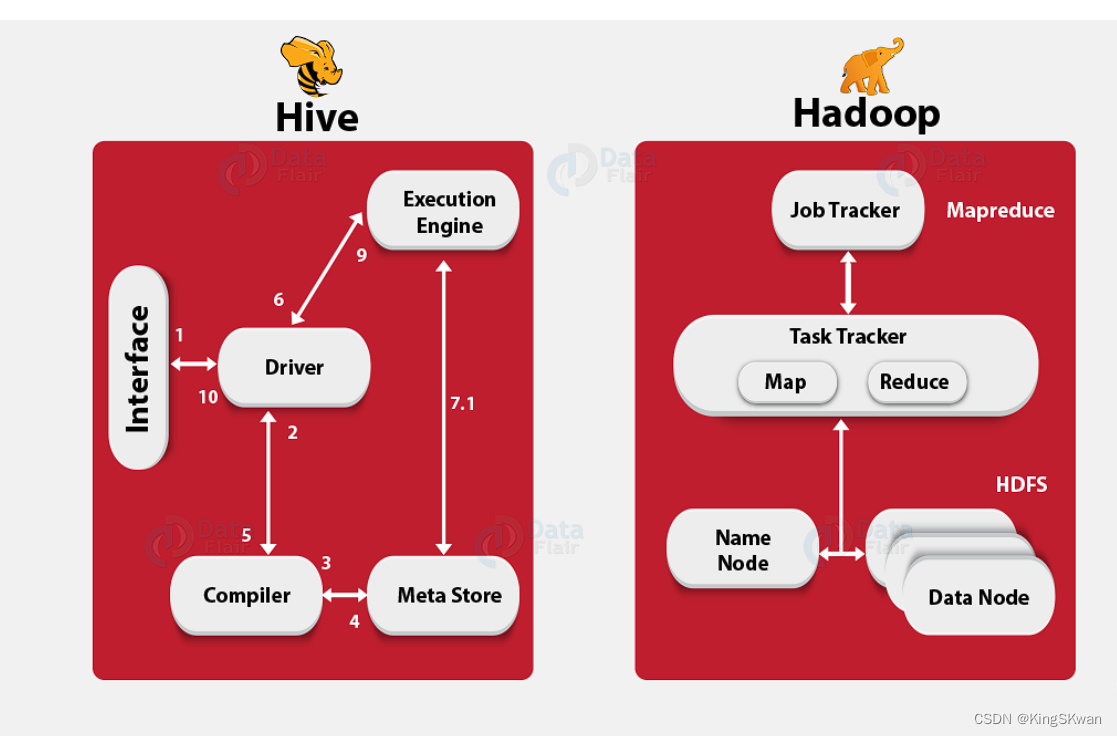
深入理解 Hadoop 上的 Hive 查询执行流程
在 Hadoop 生态系统中,Hive 是一个重要的分支,它构建在 Hadoop 之上,提供了一个开源的数据仓库系统。它的主要功能是查询和分析存储在 Hadoop 文件中的大型数据集,包括结构化和半结构化数据。Hive 在数据查询、分析和汇总方面发挥…...

JS封装网页进入/退出全屏功能,兼容各大主流浏览器
1、演示 2、封装进入全屏函数 mozRequestFullScreen:兼容Firefox webkitRequestFullscreen:兼容 Chrome、Safari、Opera msRequestFullscreen:兼容:IE/Edge const enter () > {const element document.documentElementif (el…...

el-table的复选框勾选整行变色
要实现el-table的复选框勾选整行变色,你可以使用element-ui提供的row-class-name属性结合scoped slot来完成。 首先,你需要为el-table组件添加 row-class-name 属性,并给它绑定一个方法。在这个方法中,你可以根据你的业务逻辑来判…...

一步一步写线程之八线程池的完善之二数据结构封装
一、数据容器 在前面分析过,不管是线程任务的封装还是同步数据队列的封装,都是需要一个数据结构的。一用来说,如果没有什么特殊的原因,开发者都是使用STL中数据结构。比如前面经常见到的std::queue,std::deque,std::vector,std::…...

go连接数据库(原生)
根据官网文档 Go Wiki: SQL Database Drivers - The Go Programming Language 可以看到go可以连接的关系型数据库 常用的关系型数据库基本上都支持,下面以mysql为例 下载mysql驱动 打开上面的mysql链接 GitHub - go-sql-driver/mysql: Go MySQL Driver i…...
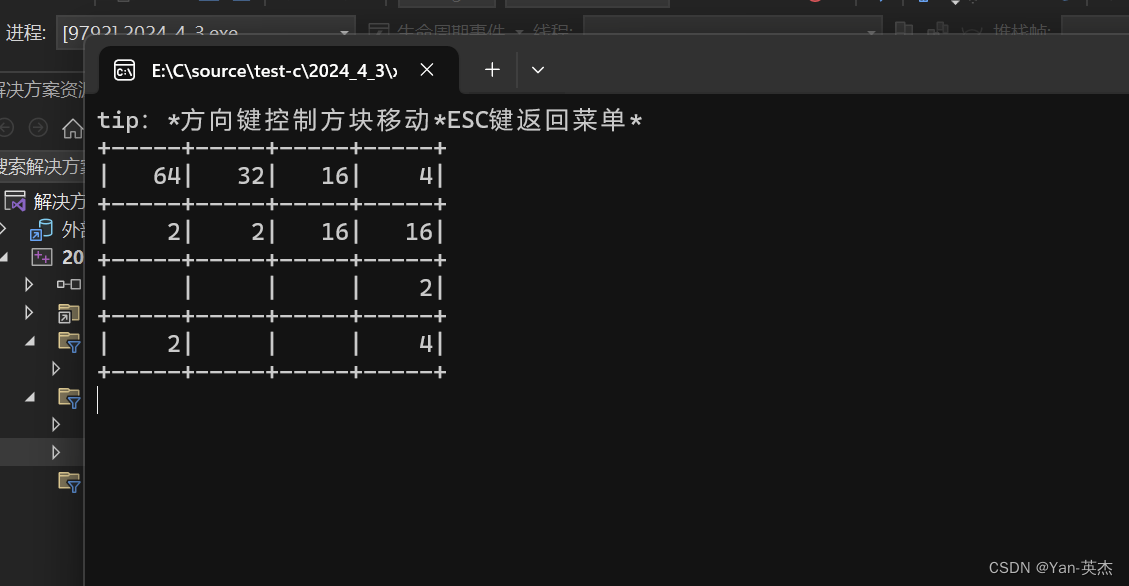
【C语言】2048小游戏【附源码】
欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 一、游戏描述: 2048是一款数字益智类游戏,玩家需要使用键盘控制数字方块的移动,合并相同数字的方块,最终达到数字方块上出现“2048”的目标。 每次移动操作,所…...
部署项目遇到的各种问题总结
文章目录 前言一、后端问题 jar包运行出现错误宝塔面板使用jdk17二、数据库问题 版本问题三、前端问题 连不上后端总结 前言 在做完项目之后,为了让别人访问到自己的网站,就需要部署前端后端以及数据库,但是在部署的过程中出现了各种问题和困…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
