Qt 总结
由于工作需要用到Qt。把过程中学习到的东西记录下来,希望能帮到他人和将来的自己。
由于需要快速实现需求,所以对Qt只是使用,并没有对原理的深入理解。
故此文只适合入门,不适合深入学习Qt。
文章目录
- 安装&维护
- 示例&教程
- 构建系统
- 编译套件
- Qt命令行环境
- 半自动的内存管理
- 信号槽机制
- GUI图形界面开发
- 打包
- 帮助文档
安装&维护
-
在线安装器
-
在qt官网下载
-
选择组件,注意选择qt的版本和编译器的版本,以及ide(qt creator)。
-
lts版本较稳定。社区版的lts版本有6.2.4,5.15.2
-
-
维护工具
-
位置在qt的安装目录
-
日后可随意增删改组件
-
-
附注: 使用国内镜像源加速
- 用命令行启动在线安装器或维护工具,并加上命令行参数–mirror https://mirror.nju.edu.cn/qt
示例&教程
- 在qt creator的欢迎界面
构建系统
- qmake/cmake
- 要使用某个模块,要先在cmake/qmake中添加
- 把 头文件/源文件/资源文件/界面文件 添加到项目中
编译套件
- windows上有mingw/msvc等
Qt命令行环境
-
功能:打包、测试、预览图形界面等
-
位置:开始菜单->所有应用->Qt-> Qt x.x.xx(xx.xx.xx)
半自动的内存管理
-
继承自QObject/QWidget的对象。可以设置父对象。所有对象可以组成一个或若干个对象树。根对象被回收时它的子孙对象会自动被回收。
-
附:c++的其他内存管理方式:raii等。
信号槽机制
- 观察者模式
- 是QObject的子孙且包含Q_OBJECT宏的类,可以声明信号或槽
- 信号:用singls宏声明,只有声明没有实现
- 槽:用slots宏声明,有实现
- 例子:
//对象1发出信号1时,对象2的信号2/槽2会被触发QObject::connect( 对象1, 信号1, 对象2, 信号2/槽2 )
//对象1发出信号1时,lambda表达式会被触发
QObject::connect( 对象1, 信号1, lambda表达式 )//手动发射信号emit 对象.信号名()
GUI图形界面开发
-
界面开发方式
- widgets-based
- 直接new控件
- ui文件
- qt quick
-
程序执行时用js引擎解析qml文件,边执行边解析渲染
-
note: 如果使用cmake,图片要添加到 cmake
-
事件处理
- connect、on信号名首字母大写
-
组件,参考:
- qt quick 核心编程 第7章
- qml 组件 https://blog.csdn.net/kenfan1647/article/details/120546294
- qml 自定义控件 https://blog.csdn.net/u013718730/article/details/104160498
- qml 自定义类型 https://blog.csdn.net/beibeix2015/article/details/111991060
-
qml与c++交互
- 此文写的很细致适合入门:https://blog.csdn.net/xiezhongyuan07/article/details/109245920
- 此文总结的很全面:https://blog.csdn.net/xiezhongyuan07/article/details/109318209
- 这是demo:https://gitee.com/xx2211/projects
- 这是进阶demo
- cpp中使用qml https://blog.csdn.net/bureau123/article/details/124454536
- qml中使用cpp https://blog.csdn.net/bureau123/article/details/124378214
-
- widgets-based
-
窗口坐标系
- 左上为原点,向右为x正方向,向下为y正方向
-
view & model
- view显示数据的容器 model存储数据 delegate定义显示方式
-
自定义控件(widget)
- 继承Qt控件,修改外观、布局、添加子控件等。
- ui设计器中使用自定义控件,先使用基本控件,再“提升为”自定义控件
-
dpi, pointSize, pixeSize
- pointSize自适应,pixelSize像素单位
打包
- windeployqt命令,有时需要手动替换依赖
- 打包成一个文件:可以使用enigma virtual box工具,但可能有许可争议
- 验证打包是否成功:可以在sandbox中尝试运行
帮助文档
- 工具栏->帮助->索引
- 在线文档 https://doc.qt.io/ https://doc.qt.io/all-topics.html
- 第三方qml教程 https://blog.csdn.net/bureau123/category_11712436.html
- 第三方qt教程 https://blog.csdn.net/bureau123/category_10691949.html
相关文章:

Qt 总结
由于工作需要用到Qt。把过程中学习到的东西记录下来,希望能帮到他人和将来的自己。 由于需要快速实现需求,所以对Qt只是使用,并没有对原理的深入理解。 故此文只适合入门,不适合深入学习Qt。 文章目录 安装&维护示例&教…...
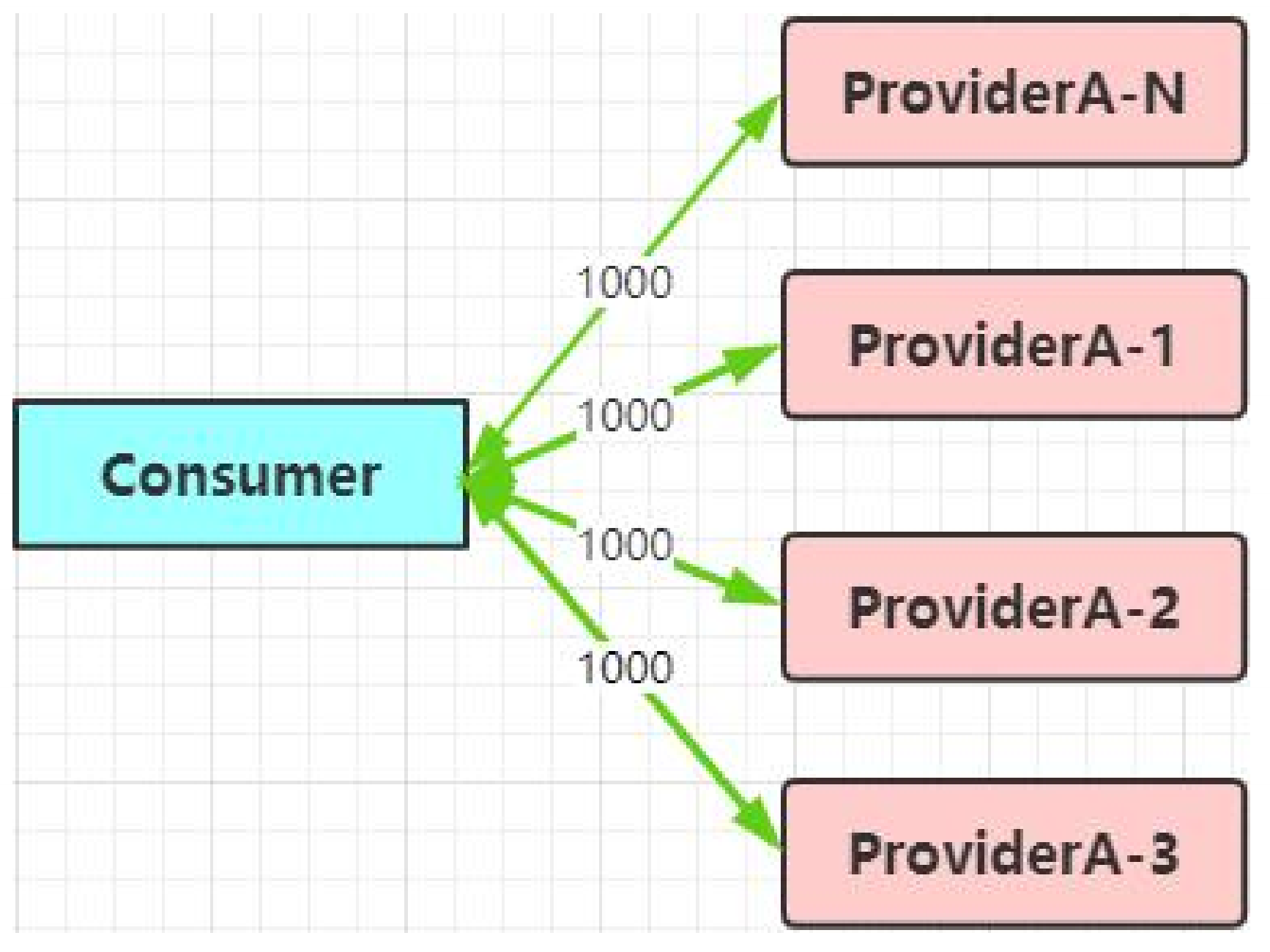
中间件复习之-RPC框架
什么是RPC框架? RPC(Remote Procedure Call):远程过程调用。当多个应用部署在多个服务器上时,由于他们不在一个内存空间上,因此需要网络来进行通信,而RPC允许它像调用本地方法一样调用远程服务。 RPC原理 服务消费方通过RPC客户…...

AcWing 787. 归并排序——算法基础课题解
AcWing 787. 归并排序 文章目录 题目描述CGo模板 题目描述 给定你一个长度为 n 的整数数列。 请你使用归并排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。 输入格式 输入共两行,第一行包含整数 n。 第二行包含 n 个整数(所有…...
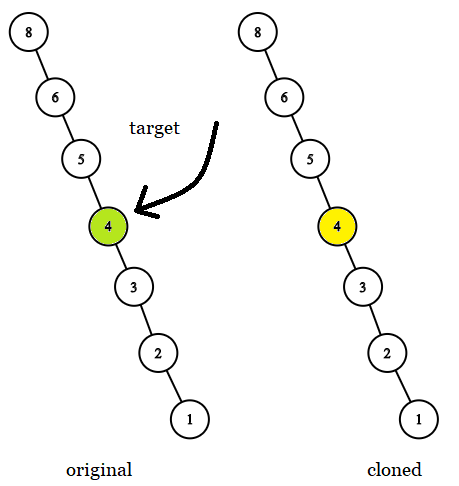
力扣1379---找出克隆二叉树的相同节点(Java、DFS、简单题)
目录 题目描述: 思路描述: 代码: (1): (2): 题目描述: 给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 ori…...
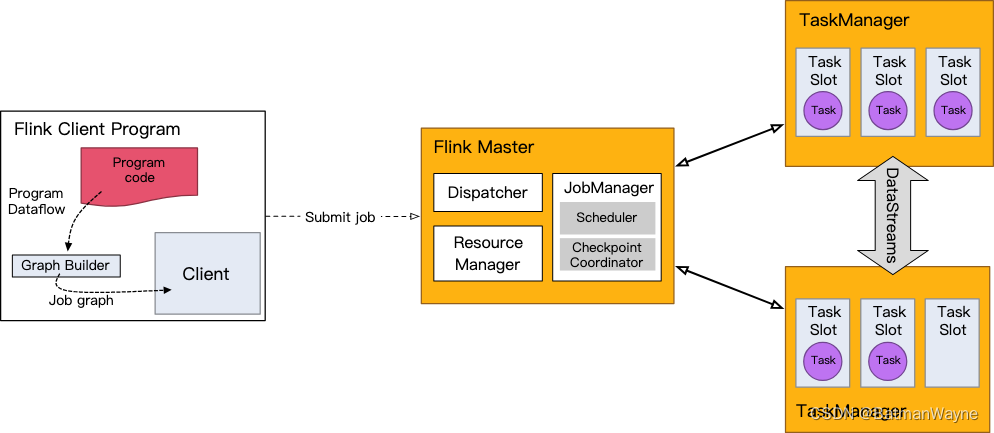
FLink学习(三)-DataStream
一、DataStream 1,支持序列化的类型有 基本类型,即 String、Long、Integer、Boolean、Array复合类型:Tuples、POJOs 和 Scala case classes Tuples Flink 自带有 Tuple0 到 Tuple25 类型 Tuple2<String, Integer> person Tuple2.…...
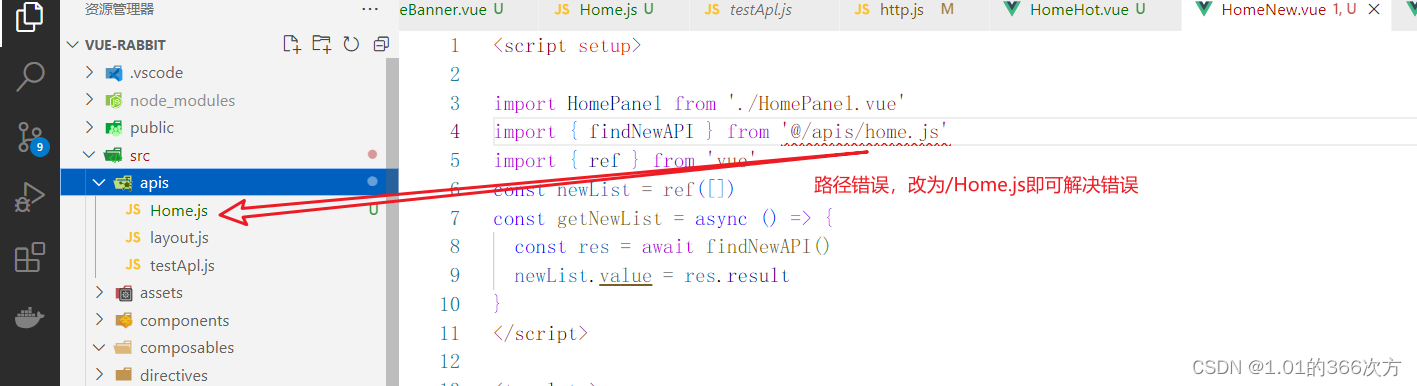
Failed to resolve import “Home/components/HomeNew.vue“. Does the file exist?
错误信息 [plugin:vite:import-analysis] Failed to resolve import "/apis/home.js" from "src/views/Home/components/HomeNew.vue". Does the file exist? 错误原因 路径错误 解决方法...

《价值》-张磊-高瓴资本-3-建立人脉和信任;顺应趋势,把握机遇;
第三章 价值投资初试炼 2005.6.1 创办高瓴资本 许多人问我为什么一直在创业,其实我倒没想到自己非要创业成功不可,只是觉得一定要做点事,做点有意义的事。归根到底,可能是“爱折腾,不满足现状,爱挑战自己”…...

游戏引擎中的物理应用
一、 角色控制器 Character Controller和普通的动态对象(Dynamic Actor )是不同的,主要的三个特点是: 它拥有可控制的刚体间的交互假设它是有无穷的摩擦力(可以站停在位置上),没有弹性加速和刹车几乎立即…...

复现k8s黄金票据学习
1.什么是黄金票据 在 Kubernetes 中,"黄金票据"并不是一个常见的术语。可能你想了解的是服务账户(Service Account)。服务账户是 Kubernetes 中用于身份验证和授权的一种机制。它们允许 Pods 或其他工作负载在 Kubernetes 集群中与…...

08-JavaScript BOM定时器及JS动画
1. 设置定时器 1.1设置超时定时器 超时调用需要使用window对象的setTimeout()方法,该方法接受两个参数:调用函数或计算表达式和以毫秒为单位的时间(即在执行代码前需要等待多少毫秒)。 //setTimeout(callback, after) //callba…...
边缘计算盒子与云计算:谁更适合您的业务需求?
边缘计算盒子和云计算,这两个概念听起来可能有点复杂,但其实它们就是两种不同的数据处理方式。那谁更适合您的业务需求呢?咱们来详细说说。 边缘计算盒子,就像是个小型的数据处理中心,放在离你业务现场比较近的地方。它…...
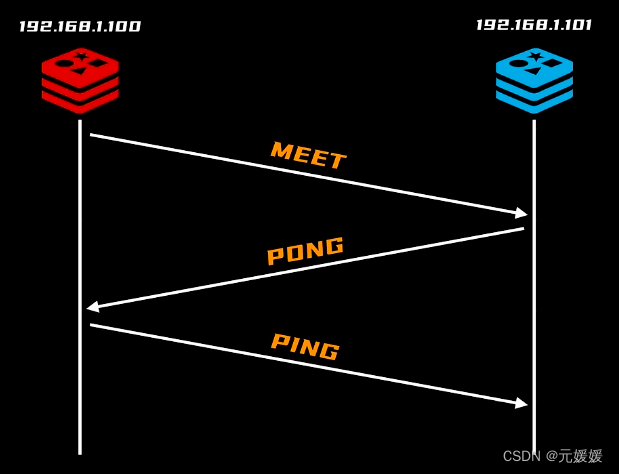
浅聊什么是Redis?
需求:MySQL面临大量的查询,即读写操作,因此类比CPU,给数据加缓存,Redis诞生。应用程序从MySQL查询的数据,在Redis设置缓存(记录在内存中,无需IO操作),后再需要…...

java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

练气第六天
问:ANR怎么分析? ANR问题,这其实是一个非常综合性的问题,因为anr会涉及CPU负载,内存空间大小,线程锁,GC回收,这里面每个点,都是非常考验我们基本功的。 分析ANR问题,需…...

认识 Redis 与 分布式
Redis 官网页面 Redis官网链接 Redis 的简介 Redis 是一个在内存中存储数据的中间件 一方面用于作为数据库,另一方面用于作为数据缓存,适用于分布式系统中 Redis 基于网络,进行进程间通信,把自己内存中的变量给别的进程…...
AWK进阶)
Linux初学(十二)AWK进阶
一、AWK 1.1 简介 AWK是Linux中重要的文本处理工具Linux三剑客只一处理的对象可以是一个具体的文件,也可以是一个命令的执行结果AWK按行读取文件,将每一行视为一条记录 案例一:获取系统中每个用户的uid 方法一:cat /etc/passwd |…...

文字识别 Optical Character Recognition,OCR CTC STN
文字识别 Optical Character Recognition,OCR 自然场景文本检测识别技术综述 将图片上的文字内容,智能识别成为可编辑的文本。 场景文字识别(Scene Text Recognition,STR) OCR(Optical Character Recognition, 光学字符识别)传统上指对输入扫描文档图像进行分析处理,识…...
四、MySQL读写分离之MyCAT
一、读写分离概述 1、什么是读写分离: 读写分离:就是将读写操作分发到不同的服务器,读操作分发到对应的服务器 (slave),写操作分发到对应的服务器(master) ① M-S (主从) 架构下&…...
通讯录项目实现
引言:通过顺序表的逻辑实现通讯录。这里就不讲关于顺序表的函数了。如果有不明白的可以看我写的顺序表的博客。 目录 顺序表与通讯录的比较 各源文件文件大榄 Contact.c中通讯录相关函数的定义 初始化和销毁通讯录 添加联系人: 删除联系人…...

xss相关知识点与绕过思路总结
前言 对xss的绕过进行了系统的学习与实践后,重新审视一下xss,对他的绕过进行一个总结。 (当然我也是个小白,这些也是我当时瞎鸡儿乱搞绕过了几个xss自己做的小总结) 可能有点丑陋,献丑了。 好博客推荐 …...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
