java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II


核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。
class Solution {public int lastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.length;i++){sum+=stones[i];}int target=sum/2;int dp[]=new int[target+1];//1、定义dp数组 3、第一列初始化为0for(int i=0;i<stones.length;i++){for(int j=target;j>=stones[i];j--){//4、遍历顺序dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);//2.递推公式}}return sum-dp[target]-dp[target];//最终的返回结果}
}
时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
空间复杂度:O(m)
494. 目标和


思路: 这道题的dp数组的含义变了。具体看代码随想录的讲解
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum=0;for(int i=0;i<nums.length;i++){sum+=nums[i];}//如果不能满足(target+sum)/2为整数的条件或target的绝对值大于sum的绝对值,直接返回0if((target+sum)%2!=0 || Math.abs(target)>Math.abs(sum)) return 0;int size=(target+sum)/2;int[] dp=new int[size+1];//1、定义dp数组,表示j容量时的表达式数目dp[0]=1;//3、初始化for(int i=0;i<nums.length;i++){for(int j=size;j>=nums[i];j--){//4、因为是01背包,所以反向遍历dp[j]=dp[j]+dp[j-nums[i]];//2、递推公式}}return dp[size];}
}
时间复杂度:O(n × m),n为正数个数,m为背包容量
空间复杂度:O(m),m为背包容量
474.一和零

思路: 这道题是一个二维的背包问题,和普通的背包相比只需要多一层对容量的循环。

class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp=new int[m+1][n+1];//1、定义dp数组,表示当0的容量为x,1的容量为n时,最大子集的长度for(int i=0;i<strs.length;i++){//4、遍历顺序,物品正序遍历int weightm=0;int weightn=0;for(int j=0;j<strs[i].length();j++){if(strs[i].charAt(j)=='0') weightm++; else weightn++;}for(int x=m;x>=weightm;x--){//4、物品的空间占用逆序遍历for(int y=n;y>=weightn;y--){dp[x][y]=Math.max(dp[x][y],dp[x-weightm][y-weightn]+1);//2、递推公式,注意value是1}}}return dp[m][n];}
}
时间复杂度: O(kmn),k 为strs的长度
空间复杂度: O(mn)
相关文章:

java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

练气第六天
问:ANR怎么分析? ANR问题,这其实是一个非常综合性的问题,因为anr会涉及CPU负载,内存空间大小,线程锁,GC回收,这里面每个点,都是非常考验我们基本功的。 分析ANR问题,需…...

认识 Redis 与 分布式
Redis 官网页面 Redis官网链接 Redis 的简介 Redis 是一个在内存中存储数据的中间件 一方面用于作为数据库,另一方面用于作为数据缓存,适用于分布式系统中 Redis 基于网络,进行进程间通信,把自己内存中的变量给别的进程…...
AWK进阶)
Linux初学(十二)AWK进阶
一、AWK 1.1 简介 AWK是Linux中重要的文本处理工具Linux三剑客只一处理的对象可以是一个具体的文件,也可以是一个命令的执行结果AWK按行读取文件,将每一行视为一条记录 案例一:获取系统中每个用户的uid 方法一:cat /etc/passwd |…...

文字识别 Optical Character Recognition,OCR CTC STN
文字识别 Optical Character Recognition,OCR 自然场景文本检测识别技术综述 将图片上的文字内容,智能识别成为可编辑的文本。 场景文字识别(Scene Text Recognition,STR) OCR(Optical Character Recognition, 光学字符识别)传统上指对输入扫描文档图像进行分析处理,识…...
四、MySQL读写分离之MyCAT
一、读写分离概述 1、什么是读写分离: 读写分离:就是将读写操作分发到不同的服务器,读操作分发到对应的服务器 (slave),写操作分发到对应的服务器(master) ① M-S (主从) 架构下&…...
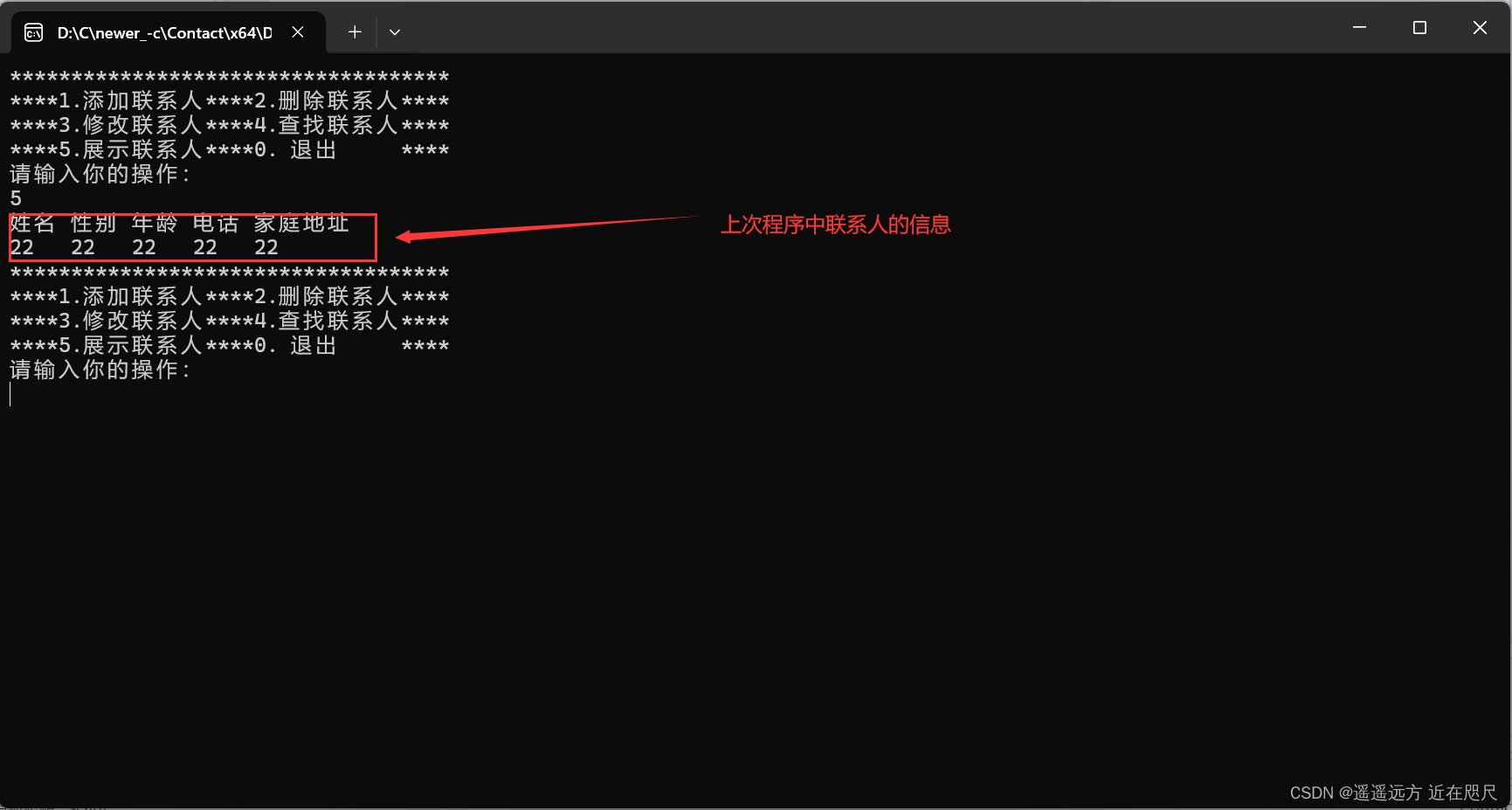
通讯录项目实现
引言:通过顺序表的逻辑实现通讯录。这里就不讲关于顺序表的函数了。如果有不明白的可以看我写的顺序表的博客。 目录 顺序表与通讯录的比较 各源文件文件大榄 Contact.c中通讯录相关函数的定义 初始化和销毁通讯录 添加联系人: 删除联系人…...

xss相关知识点与绕过思路总结
前言 对xss的绕过进行了系统的学习与实践后,重新审视一下xss,对他的绕过进行一个总结。 (当然我也是个小白,这些也是我当时瞎鸡儿乱搞绕过了几个xss自己做的小总结) 可能有点丑陋,献丑了。 好博客推荐 …...

深入解析语言模型:原理、实战与评估
引言 随着人工智能的飞速发展,语言模型作为自然语言处理(NLP)的核心技术之一,日益受到业界的广泛关注。本文旨在深入探讨语言模型的原理、实战应用以及评估方法,帮助读者更好地理解和应用这一技术。 一、语言模型原理…...

Elasticsearch 的索引优化常规项
优化常规项 https://blog.csdn.net/bairo007/article/details/132019575 1、按实际情况适当调整主分片的数量 如果主分片数量太少,会导致每个分片中的数据量过大,而且无法利用集群中所有节点的计算资源。如果主分片数量太多,会导致索引过度…...
)
【JavaParser笔记01】JavaParser解析Java源代码中的类信息(javadoc注释、类名称)
这篇文章,主要介绍如何使用JavaParser解析Java源代码中的类信息(javadoc注释、类名称)。 目录 一、JavaParser依赖库 1.1、引入依赖 1.2、获取类注释信息...
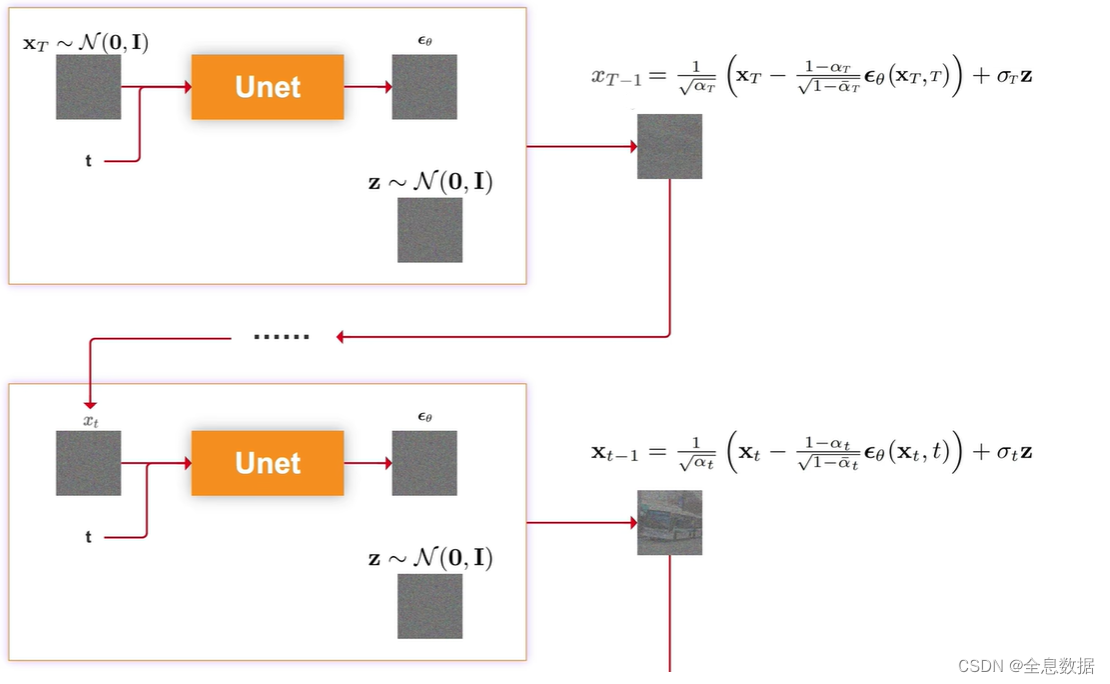
Stable Diffusion扩散模型【详解】小白也能看懂!!
文章目录 1、Diffusion的整体过程2、加噪过程2.1 加噪的具体细节2.2 加噪过程的公式推导 3、去噪过程3.1 图像概率分布 4、损失函数5、 伪代码过程 此文涉及公式推导,需要参考这篇文章: Stable Diffusion扩散模型推导公式的基础知识 1、Diffusion的整体…...

关于rabbitmq的prefetch机制
消息预取机制(Prefetch Mechanism)是RabbitMQ中用于控制消息传递给消费者的一种机制。它定义了在一个信道上,消费者允许的最大未确认的消息数量。一旦未确认的消息数量达到了设置的预取值,RabbitMQ就会停止向该消费者发送更多消息…...

机器学习介绍
机器学习是人工智能(AI)的一个分支,它使计算机系统能够从数据中学习并改进它们的性能。机器学习的核心在于开发算法,这些算法可以从大量数据中识别模式和特征,并用这些信息来做出预测或决策,而无需进行明确…...
OpenCV4.9开发之Window开发环境搭建
1.打开OpenCV所在github地址 2.点击opencv仓库,进入仓库详情,点击右下方的OpenCV 4.9.0进入下载页面 3.点击opencv-4.9.0-windows.exe下载 开始下载中... 下载完成 下载完成后,双击运行解压,默认解压路径,修改为c:/...

DDD 中的实体和值对象有什么区别?
在DDD中,实体 Entity 和值对象 Value Object 是两个基本的概念,它们之间有一些重要的区别。 唯一性:实体是唯一的,每个实体都有一个唯一的标识符,即使它的属性在一段时间内发生了变化,它仍然是这个实体。与…...

算法-最值问题
#include<iostream> using namespace std; int main() {int a[7];//上午上课时间int b[7];//下午上课时间int c[7];//一天总上课时间for (int i 0; i < 7; i) {cin >> a[i] >> b[i];c[i] a[i] b[i];}int max c[0];//max记录最长时间int index -1;//索…...

Go 性能压测工具之wrk介绍与使用
在项目正式上线之前,我们通常需要通过压测来评估当前系统能够支撑的请求量、排查可能存在的隐藏bug;压力测试(压测)是确保系统在高负载情况下仍能稳定运行的重要步骤。通过模拟高并发场景,可以评估系统的性能瓶颈、可靠…...
)
数学思想论(有目录)
数学思想是数学发展过程中的重要指导原则,它涉及对数学概念、方法和理论的理解和认识,以及如何利用这些工具来解决实际问题。数学思想的形成和演进是随着数学的发展而逐渐深化的,它体现了人类对数学本质和应用的不断探索和思考。 一些主要的数学思想包括: 函数与方程思想…...
C++的并发世界(五)——线程状态切换
0.线程状态 初始化:该线程正在被创建; 就绪:该线程在列表中就绪,等待CPU调度; 运行:该线程正在运行; 阻塞:该线程被阻塞挂机,Blocked状态包括:pendÿ…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
qt+vs Generated File下的moc_和ui_文件丢失导致 error LNK2001
qt 5.9.7 vs2013 qt add-in 2.3.2 起因是添加一个新的控件类,直接把源文件拖进VS的项目里,然后VS卡住十秒,然后编译就报一堆 error LNK2001 一看项目的Generated Files下的moc_和ui_文件丢失了一部分,导致编译的时候找不到了。因…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
