算法——最小生成树
Prim算法:
算法步骤:
1.选择一个起始节点作为最小生成树的起点。
2.将该起始节点加入最小生成树集合,并将其标记为已访问。
3.在所有与最小生成树集合相邻的边中,选择权重最小的边和它连接的未访问节点。
4.将该边和节点加入最小生成树集合,并将该节点标记为已访问。
重复步骤3和步骤4,直到最小生成树集合包含了图中的所有节点。
#include<string>
#include<algorithm>
#include<iostream>
#include<vector>
#include<queue>
using namespace std;int n;
int wei[101][101];
bool visit[101];int prim()
{int res = 0;//总共加n-1条边for (int k = 0; k < n - 1; k++){int mi = 999999;int idex;//先把节点1加入,所以是从2开始遍历for (int i = 2; i <= n; i++){if (visit[i] == 1){continue;}//找到当前已经加入的集合到其余节点的最小边的距离if (mi > wei[1][i]){mi = wei[1][i];idex = i;}}visit[idex] = 1;res += wei[1][idex];for (int i = 2; i <= n; i++){//更新当前已经加入的集合到其余节点的最小边的距离,统一以1为标记点。//新加入的为index,所以对index往外的每条边都要判断是否需要更新if (wei[idex][i] < wei[1][i]){wei[1][i] = wei[idex][i];}}}return res;
}int main()
{cin >> n;for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){cin >> wei[i][j];}}cout << prim();
}堆优化Prim算法:
算法步骤
初始化dist 数组为INF,表示所有节点到集合的距离为无穷大。
创建一个小根堆,堆中的元素为(dist 值, 节点编号)。
堆中先插入 ( 0 , 1 ) 表示节点1进入集合, dist 值为 0。
每次从堆中取出 dist 值最小的元素 (d,u),将u加入集合。
对 u 相邻的所有节点 v,更新 dist[v]=min(dist[v],g[u][v]),并更新堆中的相应元素。
重复步骤 4、5,直到所有节点都加入集合。
最后根据取出的 dist 值之和求得最小生成树权重。
#define _CRT_SECURE_NO_WARNINGS#include<iostream>
#include<cstring>
#include<vector>
#include<queue>using namespace std;const int N = 510, M = 1e5 + 10;
typedef pair<int, int> PII;
bool st[N]; // 标记节点是否已经加入最小生成树
int n, m, dist[N]; // dist数组用于记录每个节点到最小生成树的距离
int h[N], e[M], ne[M], idx, w[M]; // 邻接表存储图的边信息void add(int a, int b, int c)
{e[idx] = b; // 存储边的另一个节点w[idx] = c; // 存储边的权值ne[idx] = h[a]; // 将边插入到节点a的邻接表头部h[a] = idx++; // 更新节点a的邻接表头指针
}int Prim()
{int res = 0, cnt = 0; // res用于记录最小生成树的权值和,cnt用于记录已经选择的边数priority_queue<PII, vector<PII>, greater<PII>> heap; // 最小堆,用于选择最短边memset(dist, 0x3f, sizeof dist); // 初始化dist数组为无穷大heap.push({ 0, 1 }); // 将节点1加入最小堆,距离为0dist[1] = 0; // 节点1到最小生成树的距离为0while (heap.size()){auto t = heap.top(); // 取出最小堆中距离最小的节点heap.pop();int ver = t.second, destination = t.first; // ver为节点,destination为距离if (st[ver]) continue; // 如果节点已经在最小生成树中,跳过st[ver] = true; // 将节点标记为已经加入最小生成树res += destination; // 更新最小生成树的权值和cnt++; // 增加已选择的边数// 遍历节点ver的所有邻接边for (int i = h[ver]; i != -1; i = ne[i]){auto u = e[i]; // 邻接边的另一个节点if (dist[u] > w[i]){dist[u] = w[i]; // 更新节点u到最小生成树的距离heap.push({ dist[u], u }); // 将节点u加入最小堆}}}// 如果最小生成树的边数小于n-1,则图不连通,返回0x3f3f3f3f表示不可达if (cnt < n) return 0x3f3f3f3f;return res; // 返回最小生成树的权值和
}int main()
{cin.tie(0);ios::sync_with_stdio(false);memset(h, -1, sizeof h); // 初始化邻接表头指针为-1cin >> n >> m; // 输入节点数和边数for (int i = 0; i < m; ++i){int a, b, c;cin >> a >> b >> c;add(a, b, c), add(b, a, c); // 添加无向图的边到邻接表中}int t = Prim(); // 计算最小生成树的权值和if (t == 0x3f3f3f3f)cout << "impossible" << endl; // 输出不可达elsecout << t << endl; // 输出最小生成树的权值和return 0;
}Kruskal算法:
使用结构体存图,结构体中存放点,点,以及这两个点之间边的长度。
首先将结构体排序,按照边的大小从小到大排序。
然后按照边从小到大的顺序依次加入集合。若发现当前边已经在集合中了则跳过。
// Kruskal 算法求最小生成树 #include <cstdio>#include <string>#include <cstring>#include <iostream>#include <algorithm>using namespace std;const int maxn = 2e5 + 10; struct node {int x,y,z;}edge[maxn];bool cmp(node a,node b) {return a.z < b.z;}int fa[maxn];int n,m;int u,v,w; long long sum;int get(int x) {return x == fa[x] ? x : fa[x] = get(fa[x]);}int main(void) {scanf("%d%d",&n,&m);for(int i = 1; i <= m; i ++) {scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].z);}for(int i = 0; i <= n; i ++) {fa[i] = i;}sort(edge + 1,edge + 1 + m,cmp);// 每次加入一条最短的边for(int i = 1; i <= m; i ++) {int x = get(edge[i].x);int y = get(edge[i].y);if(x == y) continue;fa[y] = x;sum += edge[i].z;}int ans = 0;for(int i = 1; i <= n; i ++) {if(i == fa[i]) ans ++;}if(ans > 1) puts("impossible");else printf("%lld\n",sum);return 0;}
相关文章:

算法——最小生成树
Prim算法: 算法步骤: 1.选择一个起始节点作为最小生成树的起点。 2.将该起始节点加入最小生成树集合,并将其标记为已访问。 3.在所有与最小生成树集合相邻的边中,选择权重最小的边和它连接的未访问节点。 4.将该边和节点加入最小…...

OpenHarmony相机和媒体库-如何在ArkTS中调用相机拍照和录像。
介绍 此Demo展示如何在ArkTS中调用相机拍照和录像,以及如何使用媒体库接口进行媒体文件的增、删、改、查操作。 本示例用到了权限管理能力ohos.abilityAccessCtrl 相机模块能力接口ohos.multimedia.camera 图片处理接口ohos.multimedia.image 音视频相关媒体业…...
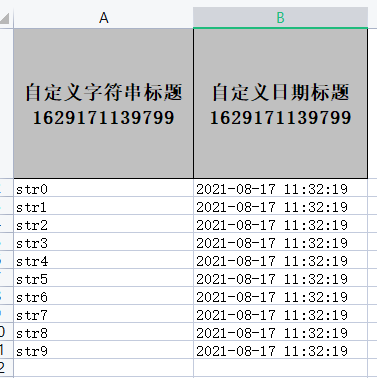
【EasyExcel】多sheet、追加列
业务-EasyExcel多sheet、追加列 背景 最近接到一个导出Excel的业务,需求就是多sheet,每个sheet导出不同结构,第一个sheet里面能够根据最后一列动态的追加列,追加多少得看运营人员传了多少需求列。原本使用的 pig4cloud 架子&…...
韩顺平 | 零基础快速学Python
环境准备 开发工具:IDLE、Pycharm、Sublime Text、Eric 、文本编辑器(记事本/editplus/notepad) Python特点:既支持面向过程OOP、也支持面向对象编程;具有解释性,不需要编程二进制代码,可以直…...
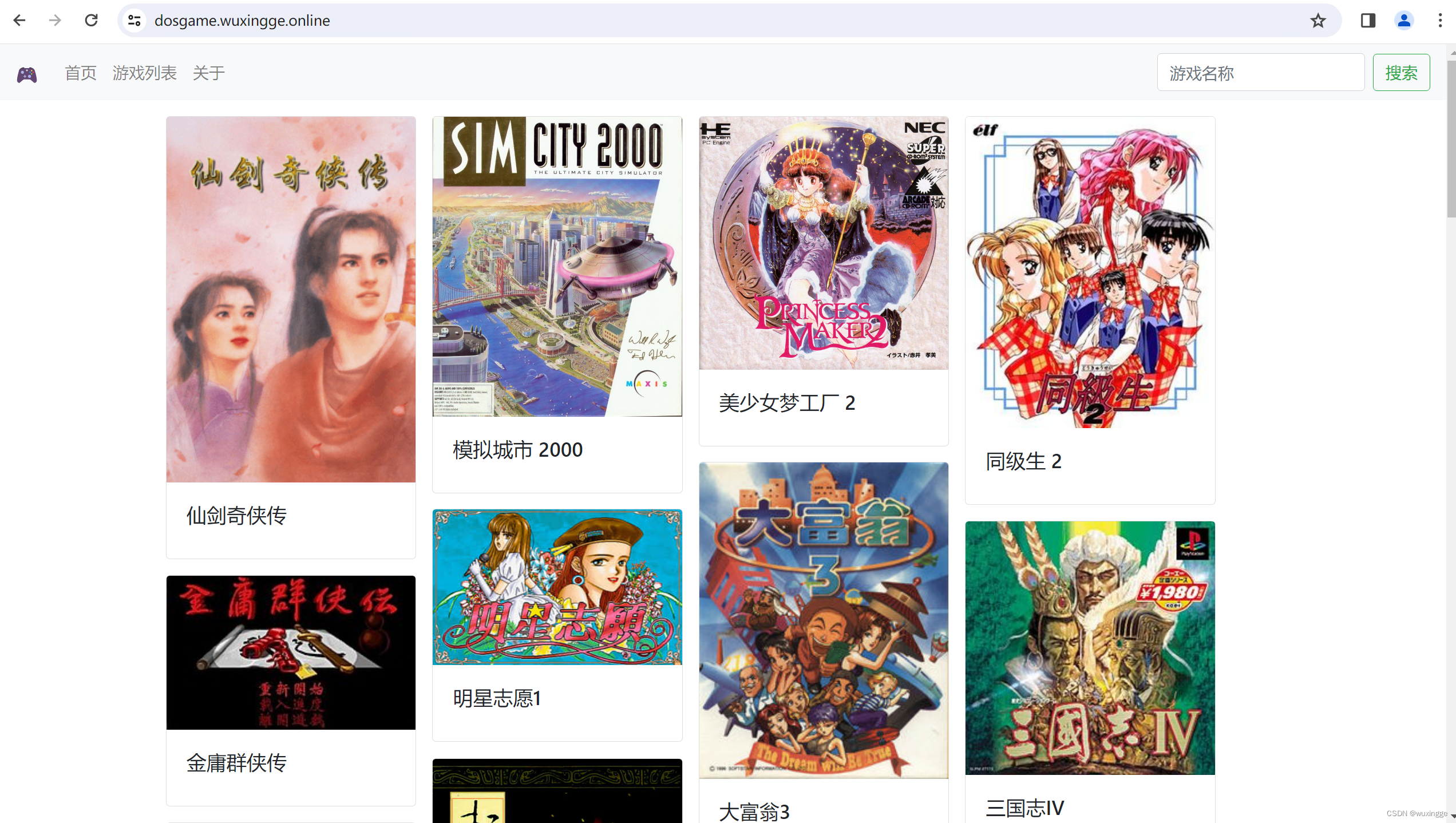
docker部署DOS游戏
下载镜像 docker pull registry.cn-beijing.aliyuncs.com/wuxingge123/dosgame-web-docker:latestdocker-compose部署 vim docker-compose.yml version: 3 services:dosgame:container_name: dosgameimage: registry.cn-beijing.aliyuncs.com/wuxingge123/dosgame-web-docke…...

基于单片机的无线红外报警系统
**单片机设计介绍,基于单片机的无线红外报警系统 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的无线红外报警系统是一种结合了单片机控制技术和无线红外传感技术的安防系统。该系统通过无线红外传感器实…...

【JAVAEE学习】探究Java中多线程的使用和重点及考点
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...
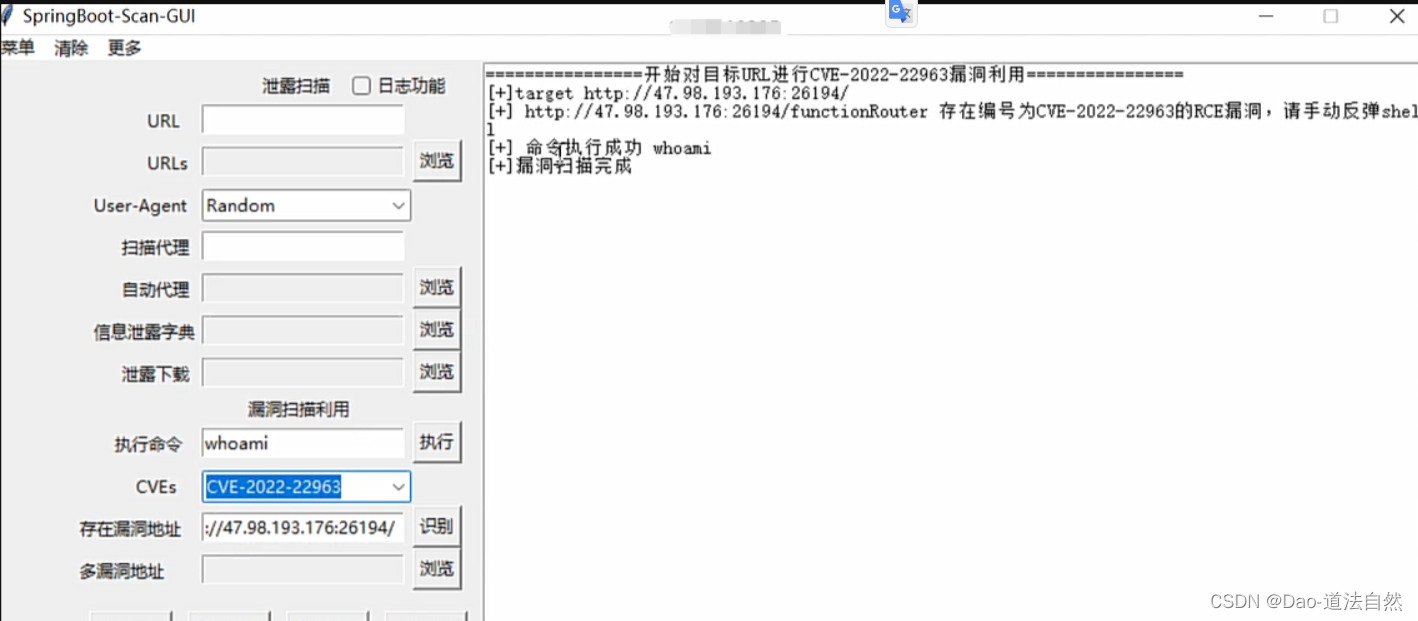
Day81:服务攻防-开发框架安全SpringBootStruts2LaravelThinkPHPCVE复现
目录 PHP-框架安全-Thinkphp&Laravel Laravel CVE-2021-3129 RCE Thinkphp 版本3.X RCE-6.X RCE 版本6.X lang RCE J2EE-框架安全-SpringBoot&Struts2 Struct2 旧漏洞(CVE-2016-0785等) struts2 代码执行 (CVE-2020-17530)s2-061 Str…...
.kat6.l6st6r勒索病毒肆虐,这些应对策略或许能帮到你
引言: 近年来,网络安全问题日益凸显,其中勒索病毒更是成为了公众关注的焦点。其中,.kat6.l6st6r勒索病毒以其独特的传播方式和破坏力,给全球用户带来了极大的困扰。本文将深入探讨.kat6.l6st6r勒索病毒的特点…...

maya移除节点 修改节点
目录 maya移除节点 使用 Maya 用户界面: 使用脚本: maya 修改节点名字 使用 Maya 用户界面: 使用 MEL 脚本: 使用 Python 脚本: 注意事项: maya移除节点 使用 Maya 用户界面: 在“层次…...

嵌入式算法开发系列之卡尔曼滤波算法
卡尔曼滤波算法 文章目录 卡尔曼滤波算法前言一、卡尔曼滤波算法原理二、算法应用三、C语言实现总结 前言 在嵌入式系统中,传感器数据通常受到噪声、误差和不确定性的影响,因此需要一种有效的方法来估计系统的状态。卡尔曼滤波算法是一种基于概率理论的…...

简述对css工程化的理解
一、css工程化解决了哪些问题 1、宏观设计:css如何组织、拆分、设计模块结构 2、编码优化:如何更好地编写css 3、构建:如何处理css,使打包结果最优 4、可维护性:最小化后续的变更成本 二、针对问题,如何解…...

.NET 5种线程安全集合
在.NET中,有许多种线程安全的集合类,下面介绍五种我们常用的线程安全集合以及他们的基本用法。 ConcurrentBag ConcurrentBag 是一个线程安全的无序包。它适用于在多线程环境中频繁添加和移除元素的情况。 ConcurrentBag<int> concurrentBag n…...
计算机信息自查
文章目录 操作系统安装时间硬盘序列号查询上网IPMAC地址 操作系统安装时间 可以使用命令行形式,查询windows系统安装时间: wmic OS get InstallDate首先显示年份,然后是月份,然后是日期,然后是安装的确切时间 或者w…...

配置vite配置文件更改项目端口、使用@别名
一、配置vite配置文件更改项目端口 vite官方文档地址:开发服务器选项 | Vite 官方中文文档 (vitejs.dev) 使用: 二、使用别名 1. 安装 types/node types/node 包允许您在TypeScript项目中使用Node.js的核心模块和API,并提供了对它们的类型…...

【LeetCode热题100】【链表】环形链表
题目链接:141. 环形链表 - 力扣(LeetCode) 判断一个链表有没有环可以用快慢指针的方法,如果没有环,那么最终可以让两个指针中一个为空,如果有环,那么快指针终会与慢指针相遇 class Solution {…...
SpringBoot整合ELK8.1.x实现日志中心教程
目录 背景 环境准备 环境安装 1.JDK安装 2.安装Elasticsearch 3.安装zookeeper 4.安装Kafka 5.安装logstash 6.安装file beat 解决方案场景 1.日志采集 1.1 应用日志配置 1.1.1 创建logback-spring.xml文件 1.1.2 创建LoggerFactory 1.1.3 trace日志的记录用法 …...

计算机网络:数据链路层 - 封装成帧 透明传输 差错检测
计算机网络:数据链路层 - 封装成帧 & 透明传输 & 差错检测 数据链路层概述封装成帧透明传输差错检测 数据链路层概述 从数据链路层来看,主机 H1 到 H2 的通信可以看成是在四段不同的链路上的通信组成的,所谓链路就是从一个节点到相邻…...

Open3D (C++) 计算点云的特征值特征向量
目录 一、算法原理二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、算法原理 针对整个点云 P = { p i } i...

Java | Leetcode Java题解之第8题字符串转换整数atoi
题目: 题解: class Solution {public int myAtoi(String str) {Automaton automaton new Automaton();int length str.length();for (int i 0; i < length; i) {automaton.get(str.charAt(i));}return (int) (automaton.sign * automaton.ans);} …...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
