线性代数笔记23--马尔可夫矩阵、傅里叶级数
1. 马尔可夫矩阵
例子
A = [ . 1 . 001 . 3 . 2 . 099 . 3 . 7 0 . 4 ] A= \begin{bmatrix} .1 & .001 & .3\\ .2 & .099 & .3\\ .7 & 0 & .4 \end{bmatrix} A= .1.2.7.001.0990.3.3.4
马尔可夫矩阵满足条件
- λ = 1 为特征值 \lambda=1为特征值 λ=1为特征值
- 其他特征值 ∀ ∣ λ i ∣ < 1 \forall |\lambda_i| \lt1 ∀∣λi∣<1
- ∀ a i j ≥ 0 , ∀ ∑ i = 0 n a i k = 1 \forall a_{ij} \ge 0, \forall \sum_{i=0}^{n}a_{ik}=1 ∀aij≥0,∀∑i=0naik=1
为什么 λ = 1 \lambda=1 λ=1一定为其特征值
A − I = [ − . 9 . 001 . 3 . 2 − . 001 . 3 . 7 0 − . 6 ] A-I= \begin{bmatrix} -.9 & .001 & .3\\ .2 & -.001 & .3\\ .7 & 0 & -.6 \end{bmatrix} A−I= −.9.2.7.001−.0010.3.3−.6
把所有非第一行加到第一行,可以把第一行变为全 0 0 0。
所以矩阵 A − I A-I A−I为奇异矩阵。
也就是向量 ( 1 , 1 , 1 ) ∈ N ( ( A − I ) ⊤ ) (1,1,1) \in N((A-I)^{\top}) (1,1,1)∈N((A−I)⊤),即 λ = 1 \lambda=1 λ=1是 A ⊤ A^{\top} A⊤的一个特征值。
引入
A ⊤ 与 A A^{\top}与A A⊤与A有相同的特征值,当 A A A为方阵时。
知乎证明
d e t A = d e t A ⊤ d e t A − λ I = d e t ( A − λ I ) ⊤ = d e t A ⊤ − λ I d e t A − λ I = d e t A ⊤ − λ I det\ A=det\ A^{\top}\\ det\ A-\lambda I=det (A-\lambda I)^\top=det\ A^{\top}-\lambda I\\ det\ A-\lambda I=det \ A^{\top}-\lambda I det A=det A⊤det A−λI=det(A−λI)⊤=det A⊤−λIdet A−λI=det A⊤−λI
对于 d e t A − λ I = 0 与 d e t A ⊤ − λ I = 0 det\ A- \lambda I=0与det A^{\top}-\lambda I=0 det A−λI=0与detA⊤−λI=0
可以将他们化为相同的主对角线的形式,即关于 λ \lambda λ的 n n n阶多项式。
所以他们的特征值相同。
对 A A A化为 R R R形式的行变化,可以同样对 A ⊤ A^{\top} A⊤施行列变换为 L L L。
且 L = R ⊤ L=R^{\top} L=R⊤。
所以 λ = 1 \lambda=1 λ=1是马尔可夫矩阵的一个特征向量。
1.1 应用
预测
u k + 1 = A u k u_{k+1}=Au_k uk+1=Auk
人口迁移
假设某一时间内, c c c州到 d d d州人口迁移组成。
A = [ 0.9 0.2 0.1 0.8 ] A=\begin{bmatrix} 0.9 & 0.2\\ 0.1 & 0.8 \end{bmatrix} A=[0.90.10.20.8]
给定初值 c d c \ d c d州人口初值,我们则可以预测未来变化。
[ u c u d ] = [ 0 1000 ] \begin{bmatrix} u_{c}\\u_{d} \end{bmatrix}= \begin{bmatrix} 0\\1000 \end{bmatrix} [ucud]=[01000]
λ 1 = 1 , λ 2 = 0.7 \lambda_1=1,\lambda_2=0.7 λ1=1,λ2=0.7
特征向量
X 1 = [ 2 1 ] X 2 = [ 1 − 1 ] X_1=\begin{bmatrix} 2\\1 \end{bmatrix} X_2=\begin{bmatrix} 1\\-1 \end{bmatrix} X1=[21]X2=[1−1]
稳态方程
u k = c 1 × 1 k [ 2 1 ] + c 2 × ( 0.7 ) k [ − 1 1 ] u_k=c_1\times 1^k\begin{bmatrix}2\\1\end{bmatrix}+c_2\times (0.7)^k\begin{bmatrix}-1\\1\end{bmatrix} uk=c1×1k[21]+c2×(0.7)k[−11]
由于
u 0 = [ 0 1000 ] u_0=\begin{bmatrix}0\\1000\end{bmatrix} u0=[01000]
可以求得
c 1 = 1000 / 3 , c 2 = 2000 / 3 c_1=1000/3,c_2=2000/3 c1=1000/3,c2=2000/3
再根据公式即可预测 k k k年后人口状况了。
2. 傅里叶级数
2.1 标准正交基的投影
给定空间 R n R^n Rn上的一组标准正交基
q 1 , q 2 ⋯ q n q_1,q_2 \cdots q_n q1,q2⋯qn
∀ 向量 V 可被表示为 v = ∑ i = 1 n x i q i \forall 向量 V可被表示为\\ v=\sum_{i=1}^{n}x_iq_i ∀向量V可被表示为v=i=1∑nxiqi
如何快速求得 x i x_i xi
q i ⊤ v = [ 0 0 ⋯ x i ⋯ 0 ] q_i^{\top}v=[0\ 0\cdots x_i\ \cdots0] qi⊤v=[0 0⋯xi ⋯0]
矩阵形式
Q X = V X = Q − 1 V = Q ⊤ V x i = q i ⊤ V QX=V\\ X=Q^{-1}V=Q^{\top}V\\ x_i=q_i^{\top}V QX=VX=Q−1V=Q⊤Vxi=qi⊤V
傅里叶级数
f ( x ) = a 0 + a 1 cos x + a 2 sin x + a 3 cos 2 x + ⋯ f ( x ) = f ( x + 2 π ) f(x)=a_0+a_1\cos x+a_2\sin x+a_3\cos2x+\cdots \\ f(x)=f(x+2\pi) f(x)=a0+a1cosx+a2sinx+a3cos2x+⋯f(x)=f(x+2π)
向量点积
v ⊤ w = v 1 w 1 + v 2 w 2 + ⋯ + v n w n v^{\top}w=v_1w_1+v_2w_2+\cdots+v_nw_n v⊤w=v1w1+v2w2+⋯+vnwn
函数内积( i n n e r p r o d u c t inner\ product inner product)
f ⊤ g = ∫ 0 2 π f ( x ) g ( x ) d x f^{\top}g=\int_{0}^{2\pi}f(x)g(x)dx f⊤g=∫02πf(x)g(x)dx
相关文章:

线性代数笔记23--马尔可夫矩阵、傅里叶级数
1. 马尔可夫矩阵 例子 A [ . 1 . 001 . 3 . 2 . 099 . 3 . 7 0 . 4 ] A \begin{bmatrix} .1 & .001 & .3\\ .2 & .099 & .3\\ .7 & 0 & .4 \end{bmatrix} A .1.2.7.001.0990.3.3.4 马尔可夫矩阵满足条件 λ 1 为特征值 \lambda1为特征…...
Elasticsearch 压测实践总结
背景 搜索、ES运维场景离不开压力测试。 1.宿主机层面变更:参数调优 & 配置调整 & 硬件升级2.集群层面变更:参数调优3.索引层面变更:mapping调整 当然还有使用层面变更,使用API调优(不属于该文章的讨论范围…...

Spirngboot JWT快速配置和使用
2、JWT 2.1、JWT介绍 JWT是JSON Web Token的缩写,即JSON Web令牌,是一种自包含令牌。 是为了在网络应用环境间传递声明而执行的一种基于JSON的开放标准。 JWT的声明一般被用来在身份提供者和服务提供者间传递被认证的用户身份信息,以便于从…...
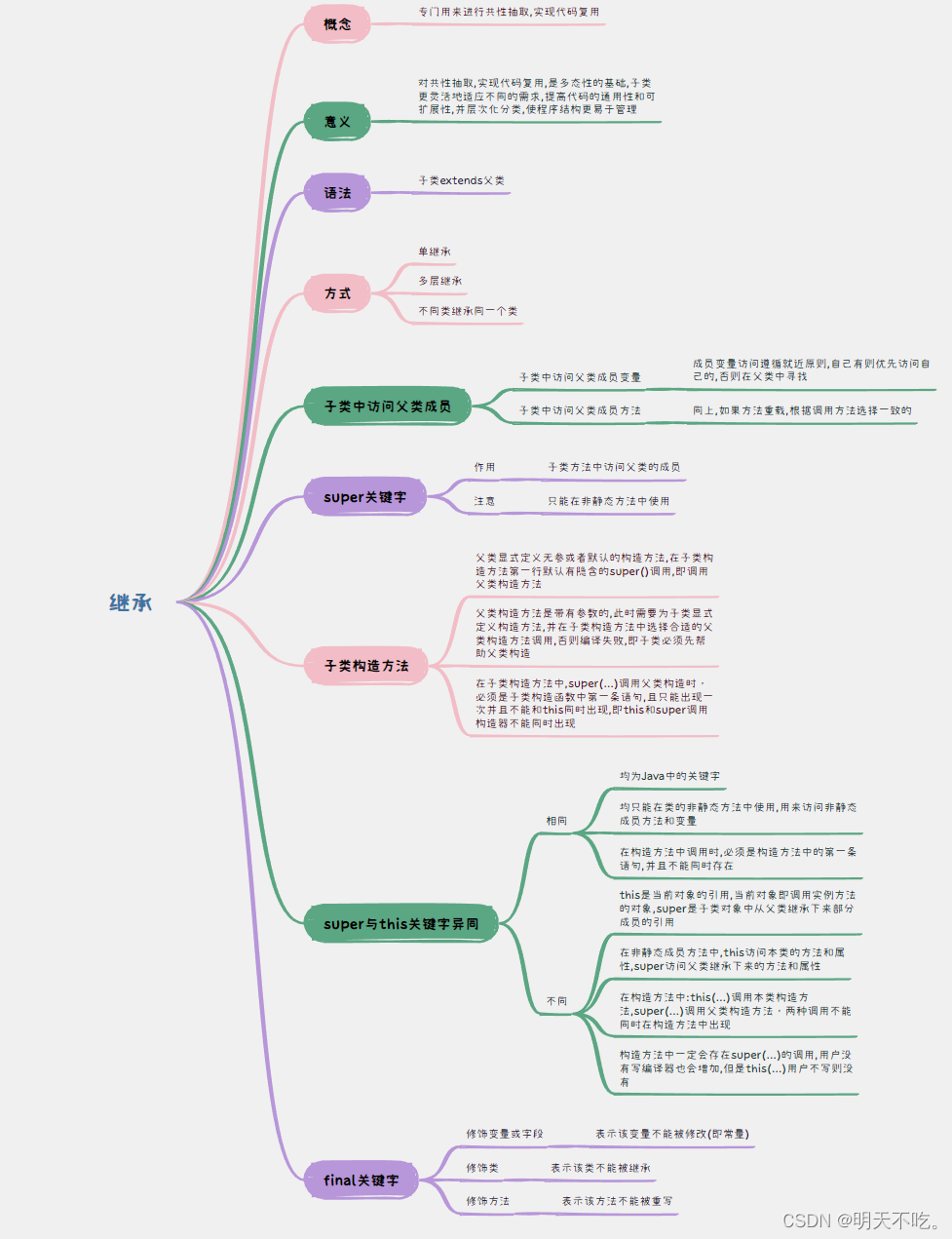
【Java SE】继承
🥰🥰🥰来都来了,不妨点个关注叭! 👉博客主页:欢迎各位大佬!👈 文章目录 1. 继承1.1 继承是什么1.2 继承的意义1.3 继承的语法1.4 继承的方式1.5 子类中访问父类成员1.5.1 子类中访问…...
:策略模式)
设计模式(19):策略模式
策略模式 策略模式对应与解决某一个问题的一个算法族,允许用户从该算法族中任选一个算法解决某一问题,同时可以方便的更换算法或者增加新的算法。并且由客户端决定调用哪个算法。 本质 分离算法,选择实现; 策略模式角色 上下…...
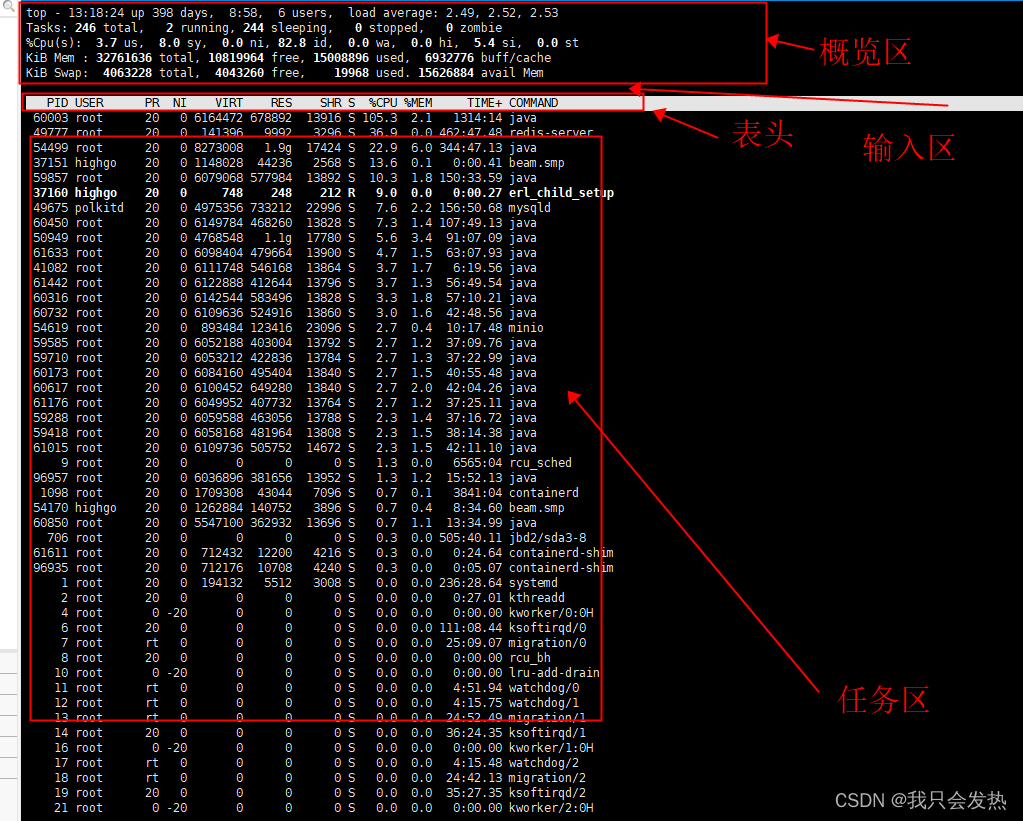
Linux 命令 top 详解
1 top命令介绍 Linux系统中,Top命令主要用于实时运行系统的监控,包括Linux内核管理的进程或者线程的资源占用情况。这个命令对所有正在运行的进程和系统负荷提供不断更新的概览信息,包括系统负载、CPU利用分布情况、内存使用、每个进程的内容…...

Android安卓开发 - 简单介绍(一)
最近呢需要重构还有维护安卓项目,所以最近会从零开始梳理开发的一些知识点以及开发的内容 前面已经写了安装的教程,idea怎么安装,还有官方的开发工具Android Studio怎么安装 2024最新版Android studio安装入门教程(非常详细&…...
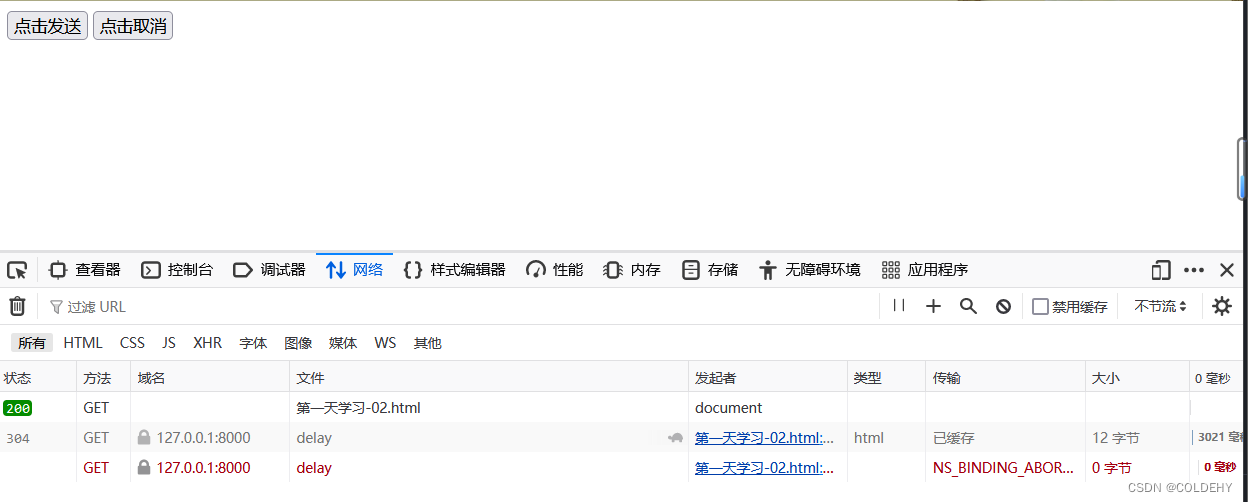
AJAX —— 学习(二)
目录 一、利用 JSON 字符串 返回数据 (一)基础代码 (二)原理及实现 二、nodmon 工具 自动重启服务 (一)用途 (二)下载 (三)使用 三、IE 缓存问题 &a…...

CSC博士联培申请时间线
暂时只记得这么多了,有问题会及时修改。 #mermaid-svg-ZMjY9etaS7StCVuw {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-ZMjY9etaS7StCVuw .error-icon{fill:#552222;}#mermaid-svg-ZMjY9etaS7StCVuw .e…...
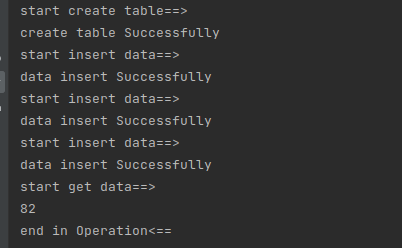
大数据实验三-HBase编程实践
目录 一.实验内容 二.实验目的 三.实验过程截图及说明 1、安装HBase 2、配置伪分布式模式: 3、使用hbase的shell命令来操作表: 4、使用hbase提供的javaAPI来编程实现类似操作: 5、实验总结及心得体会…...

【Python】Pillow支持的图像文件格式
完全支持格式只读格式只写格式仅标识格式BLPCURPALMBUFRBMPDCXPDFGRIBDDSFITSXV ThumbnailsHDF5DIBFLCMPEGEPSFPXGIFFTEXICNSGBRICOGDIMIMTJPEGIPTC/NAAJPEG 2000MCIDASMSPMICPCXMPOPNGPCDPPMPIXARSGIPSDSPIDERQOITGASUNTIFFWALwebpWMF、EMFXBMXPM 参考文献 图像文件格式 - P…...

算法——最小生成树
Prim算法: 算法步骤: 1.选择一个起始节点作为最小生成树的起点。 2.将该起始节点加入最小生成树集合,并将其标记为已访问。 3.在所有与最小生成树集合相邻的边中,选择权重最小的边和它连接的未访问节点。 4.将该边和节点加入最小…...

OpenHarmony相机和媒体库-如何在ArkTS中调用相机拍照和录像。
介绍 此Demo展示如何在ArkTS中调用相机拍照和录像,以及如何使用媒体库接口进行媒体文件的增、删、改、查操作。 本示例用到了权限管理能力ohos.abilityAccessCtrl 相机模块能力接口ohos.multimedia.camera 图片处理接口ohos.multimedia.image 音视频相关媒体业…...
【EasyExcel】多sheet、追加列
业务-EasyExcel多sheet、追加列 背景 最近接到一个导出Excel的业务,需求就是多sheet,每个sheet导出不同结构,第一个sheet里面能够根据最后一列动态的追加列,追加多少得看运营人员传了多少需求列。原本使用的 pig4cloud 架子&…...
韩顺平 | 零基础快速学Python
环境准备 开发工具:IDLE、Pycharm、Sublime Text、Eric 、文本编辑器(记事本/editplus/notepad) Python特点:既支持面向过程OOP、也支持面向对象编程;具有解释性,不需要编程二进制代码,可以直…...
docker部署DOS游戏
下载镜像 docker pull registry.cn-beijing.aliyuncs.com/wuxingge123/dosgame-web-docker:latestdocker-compose部署 vim docker-compose.yml version: 3 services:dosgame:container_name: dosgameimage: registry.cn-beijing.aliyuncs.com/wuxingge123/dosgame-web-docke…...

基于单片机的无线红外报警系统
**单片机设计介绍,基于单片机的无线红外报警系统 文章目录 一 概要二、功能设计设计思路 三、 软件设计原理图 五、 程序六、 文章目录 一 概要 基于单片机的无线红外报警系统是一种结合了单片机控制技术和无线红外传感技术的安防系统。该系统通过无线红外传感器实…...

【JAVAEE学习】探究Java中多线程的使用和重点及考点
˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如…...
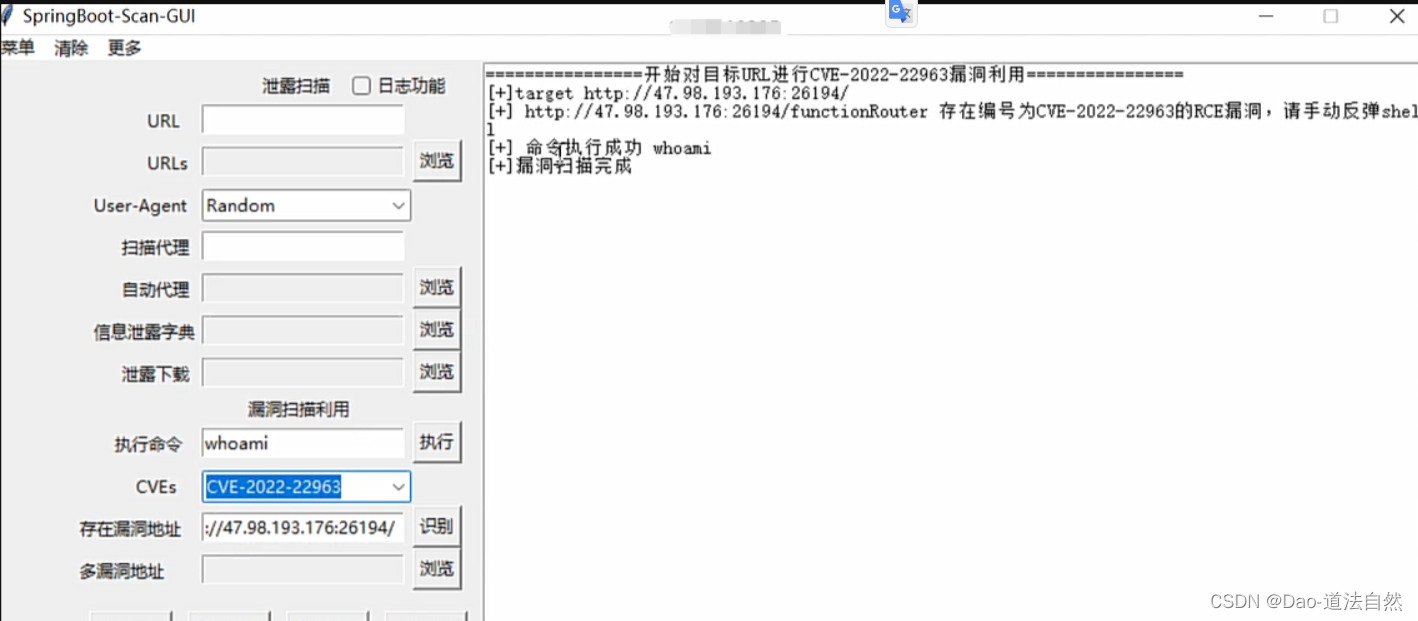
Day81:服务攻防-开发框架安全SpringBootStruts2LaravelThinkPHPCVE复现
目录 PHP-框架安全-Thinkphp&Laravel Laravel CVE-2021-3129 RCE Thinkphp 版本3.X RCE-6.X RCE 版本6.X lang RCE J2EE-框架安全-SpringBoot&Struts2 Struct2 旧漏洞(CVE-2016-0785等) struts2 代码执行 (CVE-2020-17530)s2-061 Str…...
.kat6.l6st6r勒索病毒肆虐,这些应对策略或许能帮到你
引言: 近年来,网络安全问题日益凸显,其中勒索病毒更是成为了公众关注的焦点。其中,.kat6.l6st6r勒索病毒以其独特的传播方式和破坏力,给全球用户带来了极大的困扰。本文将深入探讨.kat6.l6st6r勒索病毒的特点…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

python读取SQLite表个并生成pdf文件
代码用于创建含50列的SQLite数据库并插入500行随机浮点数据,随后读取数据,通过ReportLab生成横向PDF表格,包含格式化(两位小数)及表头、网格线等美观样式。 # 导入所需库 import sqlite3 # 用于操作…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...

day51 python CBAM注意力
目录 一、CBAM 模块简介 二、CBAM 模块的实现 (一)通道注意力模块 (二)空间注意力模块 (三)CBAM 模块的组合 三、CBAM 模块的特性 四、CBAM 模块在 CNN 中的应用 一、CBAM 模块简介 在之前的探索中…...

Java高级 |【实验八】springboot 使用Websocket
隶属文章:Java高级 | (二十二)Java常用类库-CSDN博客 系列文章:Java高级 | 【实验一】Springboot安装及测试 |最新-CSDN博客 Java高级 | 【实验二】Springboot 控制器类相关注解知识-CSDN博客 Java高级 | 【实验三】Springboot 静…...
