运筹学经典问题(八):CVRP和VRP-TW
文章目录
- 问题描述
- 问题建模
- 决策变量
- 数学建模
- 基于容量的消除子环的约束 (load-based SECs)
- CVRP完整的数学模型
- 加上时间窗限制的CVRP
问题描述
给定一个图,图上的点代表客户,边代表客户之间的路线,边的权重代表客户之间的距离,点上的数字代表每个用户的需求量。
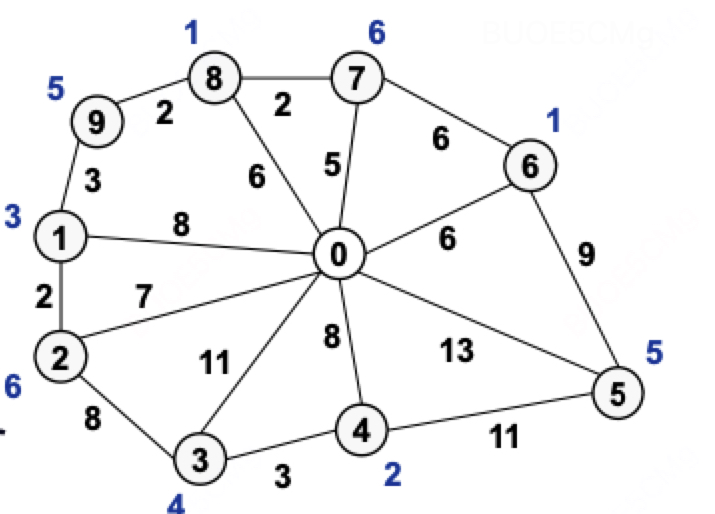
数学符号表示如下:

本文讨论的问题背景:
- 用户需求已知,且被一辆车满足(不要拆开);
- 有 m m m辆车,且有相同的最大载量 L L L;
- 路网络是对称的(往返距离一样,不考虑上下坡之类的问题);
- 要么取货要么送货;
- 1个仓库,而且车的路线 T T T要是闭环的(最后要回到仓库);
- 只考虑1个规划周期;
- 目标是最小化车辆的行驶距离;
- 点0代表仓库。
问题建模
决策变量

数学建模
疑问:这种建模方式怎么知道每辆车的路线?
会有图上的哪些边被选中,形成 m m m个环,就知道啦!
目标函数:最小化行驶距离
m a x ∑ i , j ∈ V , i ≠ j x i j ∗ c i j max \sum_{i,j \in V, i \neq j}x_{ij}*c_{ij} max∑i,j∈V,i=jxij∗cij
约束1:车辆从每个客户出发一次
∑ j ∈ V , i ≠ j x i j = 1 , ∀ i ∈ V − { 0 } \sum_{j \in V, i \neq j}x_{ij} = 1, \forall i \in V-\{0\} ∑j∈V,i=jxij=1,∀i∈V−{0}
约束2:车辆进入每个客户一次
∑ j ∈ V , i ≠ j x j i = 1 , ∀ i ∈ V − { 0 } \sum_{j \in V, i \neq j}x_{ji} = 1, \forall i \in V-\{0\} ∑j∈V,i=jxji=1,∀i∈V−{0}
约束3:最多用 m m m辆车
∑ j ∈ V − { 0 } x 0 j ≤ m \sum_{j \in V-\{0\}}x_{0j} \leq m ∑j∈V−{0}x0j≤m
如果只是上面的模型,可能会出现下图这种解,右下角这个环没有包含仓库!因此,我们需要一个约束去消除这种不包含仓库的子环。此外,上面的约束也没有约束车辆的容量限制!这也是VRP建模的一个略难的约束。
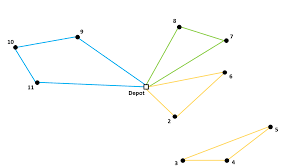
基于容量的消除子环的约束 (load-based SECs)
学术上称为Sub-tour-elimination constraints (SECs),该约束需要保证:
1. 每个环路不超过车辆最大容量;
2. 每个环路都包含仓库。
新引入一个变量:
u i u_i ui: 假设我们的问题是车辆去客户那里取货, u i u_i ui表示车辆到达客户点 i i i时的载量, ∀ i ∈ V \forall i \in V ∀i∈V;
因此有如下约束:
如果我们选择了 ( i , j ) (i, j) (i,j)这条连边,那么车辆到达客户 i i i时的容量,加上用户 i i i寄货的重量,要为车辆到达客户 j j j时的容量。逻辑上是相等的,但是我理解是为了刻画这个等式的成立是基于 ( i , j ) (i, j) (i,j)这条连边被选择,所以描述成了下面的 ≤ \leq ≤的形式。
u i + b i ≤ u j + ( 1 − x i j ) L , ∀ i , j ∈ V − 0 , i ≠ j u_i + b_i \leq u_j + (1-x_{ij})L, \forall i,j \in V -{0},i \neq j ui+bi≤uj+(1−xij)L,∀i,j∈V−0,i=j
但是这个约束并没有刻画车辆的容量限制?
应该还要加一个:
u i ≤ L , ∀ i ∈ V u_i \leq L, \forall i \in V ui≤L,∀i∈V
CVRP完整的数学模型

加上时间窗限制的CVRP
假设某些客户只想在特定时间段被服务,那么在上述问题的基础上,我们需要引入如下新的常量定义:

同时,我们需要引入一个新的决策变量:
a i a_i ai:到达客户 i i i时的时间, ∀ i ∈ V \forall i \in V ∀i∈V
新增的约束包括:
1. 定义到达第一个客户的时间:
t 0 j x i j ≤ a j , ∀ j ∈ V t_{0j}x_{ij} \leq a_j, \forall j \in V t0jxij≤aj,∀j∈V
2. 约束两个连续访问的用户的时间:访问用户 i i i的时间+用户 i i i被服务的时间+从 i i i到 j j j的形式时间 = 访问用户 j j j的时间
a i + s i + t i j ≤ a j + ( 1 − x i j ) T , ∀ i , j ∈ V − 0 , i ≠ j a_i + s_i + t_{ij} \leq a_j + (1-x_{ij})T, \forall i,j \in V-0, i \neq j ai+si+tij≤aj+(1−xij)T,∀i,j∈V−0,i=j
3. 约束每个用户被访问的时间在指定时间窗内:
w i s ≤ a i , ∀ i ∈ V − 0 w_i^s \leq a_i, \forall i \in V-0 wis≤ai,∀i∈V−0
a i + s i ≤ w i e , ∀ j ∈ V − 0 a_i + s_i \leq w_i^e, \forall j \in V-0 ai+si≤wie,∀j∈V−0
相关文章:

运筹学经典问题(八):CVRP和VRP-TW
文章目录 问题描述问题建模决策变量数学建模基于容量的消除子环的约束 (load-based SECs) CVRP完整的数学模型加上时间窗限制的CVRP 问题描述 给定一个图,图上的点代表客户,边代表客户之间的路线,边的权重代表客户之间…...
)
AI与技术美术(TechArt)
AI技术与TA 人工智能(AI)技术在技术美术(TechArt)领域的应用,为创业者开辟了一片新的天地。技术美术作为一个跨学科领域,融合了传统美术和现代技术,特别是AI技术,以创造新型的艺术表…...
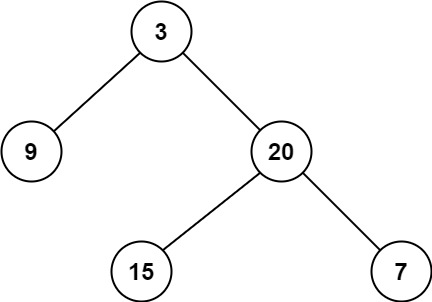
二叉树层序遍历 及相关题目
1,力扣102 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例…...

【前端面试3+1】11 http和https有何不同及https的加密过程、数组有哪些方法及作用、tcp三次握手四次挥手、【分发饼干】
一、http和https有何不同?https的加密过程 1、不同: HTTP和HTTPS的主要区别在于安全性。HTTP是超文本传输协议,是一种用于传输数据的协议,但是传输的数据是明文的,容易被窃听和篡改。而HTTPS是在HTTP基础上加入了SSL/T…...
替代 Redis 和 Memcached:25 倍吞吐量! | 开源日报 No.213
dragonflydb/dragonfly Stars: 22.4k License: NOASSERTION Dragonfly 是一个内存数据存储,适用于现代应用工作负载,可替代 Redis 和 Memcached。与传统的内存数据存储相比,Dragonfly 提供了 25 倍的吞吐量、更高的缓存命中率和更低尾部延…...

Qt与OpenCV实现图像模板匹配
在 Qt 中使用 OpenCV 实现模板匹配可以通过集成 OpenCV 库和使用其相关函数来完成。以下是一般的步骤: 安装 OpenCV:首先,确保你已经安装了 OpenCV 库,并将其配置到你的开发环境中。 创建 Qt 项目:使用 Qt creator 或…...

OpenHarmony实战:CMake方式组织编译的库移植
以double-conversion库为例,其移植过程如下文所示。 源码获取 从仓库获取double-conversion源码,其目录结构如下表: 表1 源码目录结构 名称描述double-conversion/cmake/CMake组织编译使用到的模板double-conversion/double-conversion/源…...

Linux云计算之Linux基础3——Linux基本认识操作
1、终端 终端(terminal):人和系统交互的必要设备,人机交互最后一个界面(包含独立的输入输出设备) 物理终端(console):直接接入本机器的键盘设备和显示器虚拟终端(tty):通过软件方式虚拟实现的终端。它可以…...
canvas画图,画矩形、圆形、直线可拖拽移动,可拖拽更改尺寸大小
提示:canvas画图,画矩形,圆形,直线,曲线可拖拽移动 文章目录 前言一、画矩形,圆形,直线,曲线可拖拽移动总结 前言 一、画矩形,圆形,直线,曲线可拖…...

Github 2024-04-04 Go开源项目日报 Top10
根据Github Trendings的统计,今日(2024-04-04统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Go项目10Python项目1Prometheus监控系统和时间序列数据库 创建周期:4149 天开发语言:Go协议类型:Apache License 2.0Star数量:52463 个Fork…...

并发与限流实战:如何利用 RabbitMQ 在 SpringBoot 应用中实现并发控制与流量限制
在高并发场景下,如大促销、秒杀等,我们可以采用 RabbitMQ 配合 SpringBoot 来实现并发控制与流量限制。你可以将 RabbitMQ 作为一个缓冲区,暂存大量并发请求,然后消费者可以根据自身处理能力去处理这些请求。下面就以一个高并发订…...

VUE实现下一页的功能
实现步骤:1、确定分页参数:确定当前页码和每页显示的数量;2、获取数据:使用vue的axios或其他http库向后端发送请求,传递当前页码和每页显示的数量作为参数;3、更新数据:在vue组件中,…...

GraalVM运行模式和企业级应用
文章目录 GraalVM运行模式JIT模式AOT模式 GraalVM的问题和解决方案GraalVM企业级应用传统架构的问题Serverless架构函数计算Serverless应用场景Serverless应用 GraalVM内存参数 GraalVM运行模式 JIT模式 JIT( Just-In-Time )模式 ,即时编译模…...
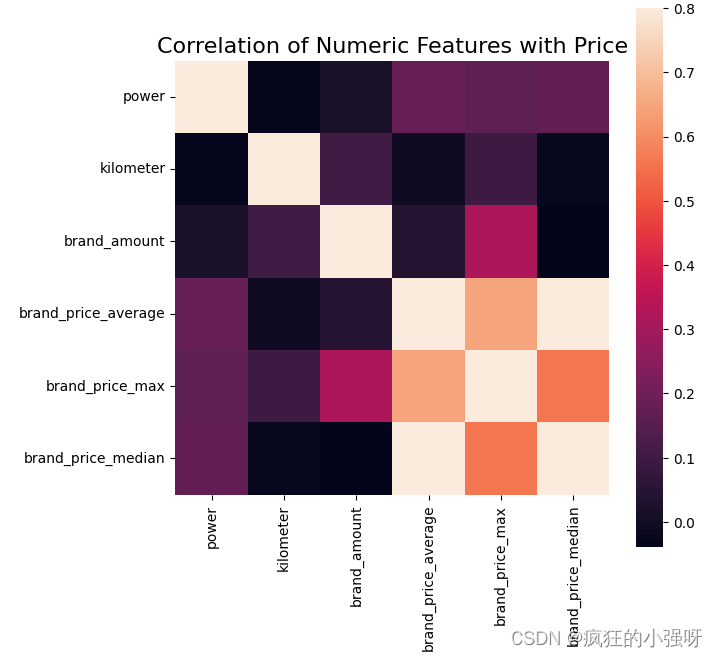
数据挖掘入门项目二手交易车价格预测之特征工程
文章目录 目标常见的特征工程具体步骤1. 导入数据2. 删除异常值3. 特征构造3.1 为树模型构造特征3.2 为LR NN 之类的模型构造特征 4. 特征筛选过滤式包裹式嵌入式 5. 总结 本文数据集来自阿里天池:https://tianchi.aliyun.com/competition/entrance/231784/informat…...
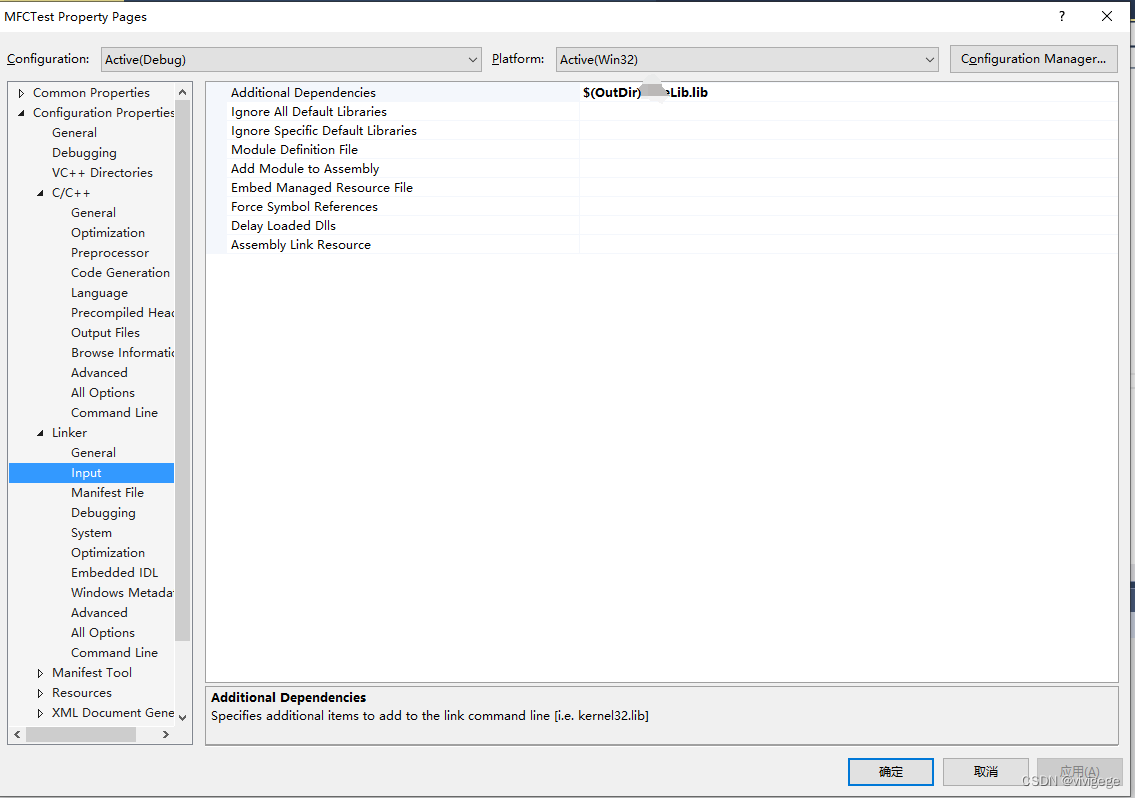
MFC通用静态库制作与使用
开发环境VS2013 1、新建工程,选择Win32 Project,命名,选择路径等 2、选择Static library ,勾选MFC 3、点击完成。在工程中添加相应的头文件、源文件等通用功能函数或者类。 4、在其他工程引入使用。在使用的工程项目设置中Linker…...

点亮创意:ChatGPT如何搭桥DALL-E图像编辑新纪元
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
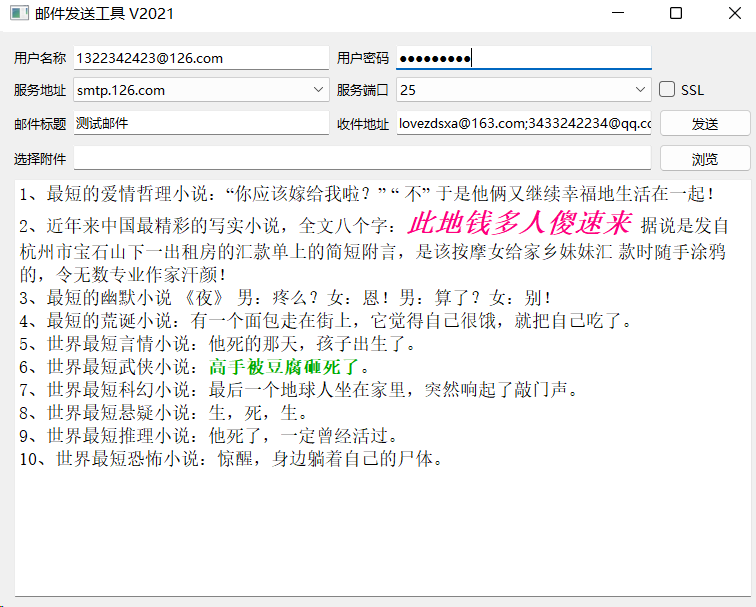
《QT实用小工具·十二》邮件批量发送工具
1、概述 源码放在文章末尾 该项目实现了邮件的批量发送,如下图所示: 项目部分代码如下所示: #ifndef SMTPCLIENT_H #define SMTPCLIENT_H#include <QtGui> #include <QtNetwork> #if (QT_VERSION > QT_VERSION_CHECK(5,0,…...

4.2总结
了解了部分Api的使用并学习了接口的API API API包含了较多种类(System,Runtime等) System其实就是一个工具类,提供了一些与系统相关的方法 下面有一些常间的System方法 方法名说明public static void exit (int status)终止当前运行的ja…...
ArcGIS 10.8中文版详细安装教程(附安装包)
ArcGIS 10.8中文版详细安装教程(附安装包) 关键词:ArcGIS 10.8中文版安装 1.概述 ArcGIS Desktop 10.8中文版是由ESRI公司开发的一款专业的地理信息系统,一套完整的桌面GIS软件套件,它包含ArcMap、ArcCatalog、ArcG…...

什么是EL表达式?怎么使用?
文章目录 一、什么是EL表达式1、命令格式:${作用域对象别名.共享数据} 二、EL表达式与作用域对象别名1、JSP文件可以使用的作用域对象2、EL表达式提供作用域对象别名3、EL表达式将引用对象属性写入到响应体4、EL表达式简化版 三、EL表达式与运算表达式四、EL表达式提…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
