openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint
文章目录
- openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint
- 256.1 功能描述
- 256.2 语法格式
- 256.3 参数说明
openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint
256.1 功能描述
设置本次查询执行内生效的查询优化相关GUC参数。hint的推荐使用场景可以参考各guc参数的说明,此处不作赘述。
256.2 语法格式
set(param value)
256.3 参数说明
-
param表示参数名。
-
value表示参数的取值。
-
目前支持使用Hint设置生效的参数有
-
布尔类:
enable_bitmapscan, enable_hashagg,enable_hashjoin, enable_indexscan,enable_indexonlyscan, enable_material,enable_mergejoin, enable_nestloop,enable_index_nestloop, enable_seqscan,enable_sort, enable_tidscan,partition_iterator_elimination,partition_page_estimation,enable_functional_dependency,var_eq_const_selectivity,enable_inner_unique_opt
-
整形类:
query_dop
-
浮点类:
cost_weight_index、default_limit_rows、seq_page_cost、random_page_cost、cpu_tuple_cost、cpu_index_tuple_cost、cpu_operator_cost、effective_cache_size
-
枚举类型:
try_vector_engine_strategy
-
说明:
- 设置不在白名单中的参数,参数取值不合法,或hint语法错误时,不会影响查询执行的正确性。使用explain(verbose on)执行可以看到hint解析错误的报错提示。
- GUC参数的hint只在最外层查询生效——子查询内的GUC参数hint不生效。
- 视图定义内的GUC参数hint不生效。
- CREATE TABLE … AS … 查询最外层的GUC参数hint可以生效。
👍 点赞,你的认可是我创作的动力!
⭐️ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!

相关文章:

openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint
文章目录 openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint256.1 功能描述256.2 语法格式256.3 参数说明 openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint 256.1 功能描述 设置本次查询执行内生效的…...

flex:1的作用是什么?
占满剩余的高度 <div classfather><div classson1></div><div classson2></div> </div>当给father添加display:flex之后,假设给son2添加flex:1,那么son2将会占满除son1之外的高度...

Mysql安装(命令方式安装)
下载mysql压缩包 Mysql可以使用界面安装,也可以使用命令的方式安装,今天我们使用命令的方式安装mysql。首先下载mysql压缩包(下载地址:https://dev.mysql.com/downloads/mysql/),解压到你想要安装的目录。 …...
)
Vben Admin实战-系统管理之用户管理-(第12节)
系列文章目录 第一节:Vben Admin介绍和初次运行 第二节:Vben Admin 登录逻辑梳理和对接后端准备 第三节:Vben Admin登录对接后端login接口 第四节:Vben Admin登录对接后端getUserInfo接口 第五节:Vben Admin权限-前端控制方式 第六节:Vben Admin权限-后端控制方式 第七节…...

Oracle常规操作
1、查看用户和密码 select username,password from dba_users; --修改用户和密码 alter user system identified by manager; alter user system identified by values 2D594E86F93B17A1; --解锁用户 alter user system account unlock; -- 用SYSDBA身份进入数据库,然…...

「33」如何让你的直播场景增加透视感?
「33」模糊滤镜增强背景画面透视感 在直播中,背景一直是作为一种陪衬而存在的,位于主场景的后面,其实,说得更直白一些,背景的存在就犹如“绿叶”,是为了衬托红花更加艳丽。所以…… 你通过画面背景的调整,可以从整体上对视频或图片的画面进行装饰,有助于增加画面的空间…...
Macbook文件清理软件 Mac电脑清理垃圾文件怎么清理
为了维护Macbook电脑的系统健康,我们需要定期给电脑进行全面清理,清除系统垃圾文件、软件缓存和系统内存。那么好用的Macbook文件清理软件有哪些呢?今天就给大家介绍几款好用的电脑清理软件并介绍Mac电脑清理垃圾文件怎么清理。 一、Macbook…...

【Java基础】Java基础知识整合
文章目录 1. 转义字符2. 变量2.1 字符串与整型相加2.2 byte和short的区别2.3 float和double的区别2.4 char类型2.5 boolean类型2.6 自动类型转换及运算2.7 强制类型转换2.8 String的转换2.9 除法运算2.10 取模规则 3. 自增4. 逻辑运算符5. 赋值运算 6. 三元运算符:7…...
)
构建集创建、售卖、转让于一体,且基于ERC721 token的NFT平台,从编写智能合约开始(Web3项目四实战之一)
NFT 全称是 non-fungible token(非同质化代币或不可篡改代币)是记录在区块链上的唯一数字标识符,用于证明所有权和真实性。NFT 的所有权记录在区块链中,所有者可以转让,从而允许 NFT 出售和交易。任何人都可以创建 NFT,创建 NFT 几乎不需要任何编码技能。NFT 通常包含对艺…...

跨境金融区块链服务平台
跨境金融服务是因企业及个人跨境经营、交易、投资、往来等活动而产生的资金使用、调拨、配置等需求,而提供的金融服务。近年来,随着我国经济的快速稳步增长和全球化经济一体化的不断深入发展,跨境金融业务增长迅速,监管也开始转化…...

运筹学经典问题(八):CVRP和VRP-TW
文章目录 问题描述问题建模决策变量数学建模基于容量的消除子环的约束 (load-based SECs) CVRP完整的数学模型加上时间窗限制的CVRP 问题描述 给定一个图,图上的点代表客户,边代表客户之间的路线,边的权重代表客户之间…...
)
AI与技术美术(TechArt)
AI技术与TA 人工智能(AI)技术在技术美术(TechArt)领域的应用,为创业者开辟了一片新的天地。技术美术作为一个跨学科领域,融合了传统美术和现代技术,特别是AI技术,以创造新型的艺术表…...
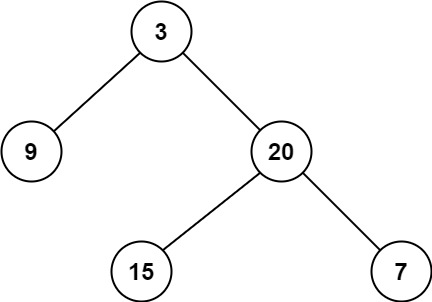
二叉树层序遍历 及相关题目
1,力扣102 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例…...

【前端面试3+1】11 http和https有何不同及https的加密过程、数组有哪些方法及作用、tcp三次握手四次挥手、【分发饼干】
一、http和https有何不同?https的加密过程 1、不同: HTTP和HTTPS的主要区别在于安全性。HTTP是超文本传输协议,是一种用于传输数据的协议,但是传输的数据是明文的,容易被窃听和篡改。而HTTPS是在HTTP基础上加入了SSL/T…...
替代 Redis 和 Memcached:25 倍吞吐量! | 开源日报 No.213
dragonflydb/dragonfly Stars: 22.4k License: NOASSERTION Dragonfly 是一个内存数据存储,适用于现代应用工作负载,可替代 Redis 和 Memcached。与传统的内存数据存储相比,Dragonfly 提供了 25 倍的吞吐量、更高的缓存命中率和更低尾部延…...

Qt与OpenCV实现图像模板匹配
在 Qt 中使用 OpenCV 实现模板匹配可以通过集成 OpenCV 库和使用其相关函数来完成。以下是一般的步骤: 安装 OpenCV:首先,确保你已经安装了 OpenCV 库,并将其配置到你的开发环境中。 创建 Qt 项目:使用 Qt creator 或…...

OpenHarmony实战:CMake方式组织编译的库移植
以double-conversion库为例,其移植过程如下文所示。 源码获取 从仓库获取double-conversion源码,其目录结构如下表: 表1 源码目录结构 名称描述double-conversion/cmake/CMake组织编译使用到的模板double-conversion/double-conversion/源…...

Linux云计算之Linux基础3——Linux基本认识操作
1、终端 终端(terminal):人和系统交互的必要设备,人机交互最后一个界面(包含独立的输入输出设备) 物理终端(console):直接接入本机器的键盘设备和显示器虚拟终端(tty):通过软件方式虚拟实现的终端。它可以…...
canvas画图,画矩形、圆形、直线可拖拽移动,可拖拽更改尺寸大小
提示:canvas画图,画矩形,圆形,直线,曲线可拖拽移动 文章目录 前言一、画矩形,圆形,直线,曲线可拖拽移动总结 前言 一、画矩形,圆形,直线,曲线可拖…...

Github 2024-04-04 Go开源项目日报 Top10
根据Github Trendings的统计,今日(2024-04-04统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Go项目10Python项目1Prometheus监控系统和时间序列数据库 创建周期:4149 天开发语言:Go协议类型:Apache License 2.0Star数量:52463 个Fork…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
MeanFlow:何凯明新作,单步去噪图像生成新SOTA
1.简介 这篇文章介绍了一种名为MeanFlow的新型生成模型框架,旨在通过单步生成过程高效地将先验分布转换为数据分布。文章的核心创新在于引入了平均速度的概念,这一概念的引入使得模型能够通过单次函数评估完成从先验分布到数据分布的转换,显…...

Razor编程中@Helper的用法大全
文章目录 第一章:Helper基础概念1.1 Helper的定义与作用1.2 Helper的基本语法结构1.3 Helper与HtmlHelper的区别 第二章:基础Helper用法2.1 无参数Helper2.2 带简单参数的Helper2.3 带默认值的参数2.4 使用模型作为参数 第三章:高级Helper用法…...
