4. python练习题4-水仙花数
4. python练习题4-水仙花数
【目录】
文章目录
- 4. python练习题4-水仙花数
- 1. 目标任务
- 2. 水仙花数的特点
- 3. 如何判断一个数是否是水仙花数?
- 4. 打印3位水仙花数
- 5. 判断一个数是不是水仙花数
- 6. 列表推导式
- 6. 列表推导式判断一个数是不是水仙花数
【正文】
1. 目标任务
水仙花数是三位数,其各位数字立方和等于该数本身,请打印所有水仙花数。
2. 水仙花数的特点
水仙花数是指一个n位数(n≥3),它的每个位上的数字的n次幂之和等于它本身。
【三位水仙花数的特点】
- 一个三位数,范围从100到999。
- 各个位上的数字的立方和等于该数本身。
【示例】
153是一个水仙花数。
因为1^3 + 5^3 + 3^3 = 153。
3. 如何判断一个数是否是水仙花数?
- 将给定的数拆分为各个位上的数字。
- 计算每个位上数字的n次幂。
- 将每个位上数字的n次幂相加。
- 判断相加的结果是否等于原始数。
4. 打印3位水仙花数
【代码示例】
# 使用range函数生成一个从100到999的整数序列
# 并将每个数字赋值给变量num
# range函数含前不含后,因此不包含1000
for num in range(100, 1000):# 通过整除运算符//将num除以100得到的商即为百位数字。hundreds = num // 100# 先将num除以10得到商,再对10取余得到十位数字tens = (num // 10) % 10# 通过对10取余运算得到个位数字ones = num % 10# 将百位、十位和个位数字的立方和与num进行比较# 如果相等,则说明该数是水仙花数if num == hundreds**3 + tens**3 + ones**3:print('%d是水仙花数。'% num)
【终端输出】
153是水仙花数。
370是水仙花数。
371是水仙花数。
407是水仙花数。
5. 判断一个数是不是水仙花数
# def 语句定义一个名为sxh的函数
# 该函数接收一个参数num
# 自定义函数以英文冒号结尾
def sxh(num):# str函数将数字(num)转换为字符串类型,以便逐位处理 num_str = str(num)# 使用len()函数获取字符串num_str的长度,并赋值给变量nn = len(num_str)# 初始化变量sum为0,用于存储各个位上数字的n次方之和 sum = 0# 遍历字符串num_str中的每个字符,将每个字符赋值给变量ifor i in num_str:# 将变量i转换为整数类型,并计算其n次方,然后加到变量sum上# 备注:sum = sum +int(digit) ** nsum += int(i) ** n# 判断变量sum是否等于参数numif sum == num:# 如果条件成立,返回Truereturn Trueelse:# 如果条件不成立,返回Falsereturn False# 测试示例
num = 153
# 调用函数sxh()判断给定的数字是否为水仙花数
if sxh(num):# 如果是水仙花数,则打印出该数字是水仙花数print('%d是水仙花数。'% num)
else:# 如果不是水仙花数,则打印出该数字不是水仙花数print('%d不是水仙花数。'% num)
【终端输出】
153是水仙花数。
6. 列表推导式
【语法】
[表达式 for 迭代变量 in 可迭代对象 if条件表达式]
【代码示例】
list4 = [ i for i in range(1,6)]
print(list4)
【终端输出】
[1, 2, 3, 4, 5]
list4 = [i for i in range(1, 6)] 是一个列表推导式。
作用是创建一个包含从1到5的整数的列表。
具体来说,它使用了一个for循环来遍历1到5 。
并将每个遍历到的元素添加到列表中。
最终,list4 的值为 [1, 2, 3, 4, 5]。
【代码示例】
list5 = [ i**2 for i in range(1,6)]
print(list5)
【终端输出】
[1, 4, 9, 16, 25]
计算输出0~5序列的所有数的平方。
【代码示例】
# 定义字符串变量num_str,其值为'123'
num_str = '123'
# len函数计算字符串num_str的长度
# 此时n的值为3,因为字符串num_str包含3个字符
n = len(num_str)
# 使用列表推导式来计算每个字符的立方和
# 表达式为:int(i) ** n
# int(i)将每个字符转换为整数类型,然后求它的n次方
# for 循环遍历num_str,num_str是字符串类型
# 因此i也是字符串类型,用int 转换为整数才能参与计算
# n=3,1的立方是1,2的立方是8,3的立方是27
# sum()函数将所有立方值相加,并将结果赋值给变量s。
s = sum(int(i) ** n for i in num_str)
print(s)
【终端输出】
36
列表推导式可参考如下链接:
90. Python列表推导式
6. 列表推导式判断一个数是不是水仙花数
# def 语句定义一个名为sxh的函数
# 该函数接受一个参数num
# 自定义函数以英文冒号结尾
def sxh(num):# str函数将数字(num)转换为字符串类型,以便逐位处理num_str = str(num)# len函数获取数字的位数n = len(num_str)# 列表推导式计算每个位上数字的n次幂之和sum_of_powers = sum(int(digit) ** n for digit in num_str)# 判断结果是否等于原始数if sum_of_powers == num:return Trueelse:return False# 测试示例
num = 153
# 调用函数sxh()判断给定的数字是否为水仙花数
if sxh(num):# 如果是水仙花数,则打印出该数字是水仙花数print('%d是水仙花数。'% num)
else:# 如果不是水仙花数,则打印出该数字不是水仙花数print('%d不是水仙花数。'% num)
【终端输出】
153是水仙花数。
相关文章:

4. python练习题4-水仙花数
4. python练习题4-水仙花数 【目录】 文章目录 4. python练习题4-水仙花数1. 目标任务2. 水仙花数的特点3. 如何判断一个数是否是水仙花数?4. 打印3位水仙花数5. 判断一个数是不是水仙花数6. 列表推导式6. 列表推导式判断一个数是不是水仙花数 【正文】 1. 目标任务…...

【Qt 学习笔记】Qt 开发环境的搭建 | Qt 安装教程
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Qt 开发环境的搭建 | Qt 安装教程 文章编号:Qt 学习笔记 /…...
ids工业相机与电控位移台同步控制及数据采集
通过VS2017和OpenCV,实现ids工业相机与电控位移台同步控制及数据采集 目录项目环境配置代码流程及思路项目架构项目开发运行效果开发关键ids相机配置位移台环境配置相机头文件相机参数设置保存图像函数设置电控位移台头文件电控位移台设置参数最后就是通过main函数进行调用和控…...

景联文科技提供高质量医疗健康AI大模型数据
医疗行业是典型的知识和技术密集型行业,其发展水平直接关系到国民健康和生命质量。 医疗健康AI大模型,作为人工智能的一个分支,能够通过学习大量的数据来生成新的数据实例,在医药研发、医学影像、医疗文本分析等都有广泛的应用前景…...

【Python第三方库】lxml 解析器和xpath路径语言
1.lxml是做什么的 是xml/html的解析器,主要是用来解析和提取html/xml数据 2.lxml语法 使用etree.HTML(html字符串),将字符串转换为Element对象通过使用Element对象.xpath(语法)提取信息,返回的是一个列表的内存地址,需要通过使用索引获取信…...
Java(Lambda、集合)、题解
一、Lambda表达式 标准格式 ()对应方法的形参 ;->固定格式 注意点: Lambda表达式可以用来简化匿名内部类的书写 Lambda表达式只能简化函数式接口的匿名内部类的写法 函数式接口: 有且仅有一个抽象方法的接口叫做函数式接口&…...
Transformer学习: Transformer小模块学习--位置编码,多头自注意力,掩码矩阵
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 Transformer学习 1 位置编码模块1.1 PE代码1.2 测试PE1.3 原文代码 2 多头自注意力模块2.1 多头自注意力代码2.2 测试多头注意力 3 未来序列掩码矩阵3.1 代码3.2 测试掩码 1 …...

easyexcel 动态列导出
1. 引入easyexcel <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.2.1</version></dependency> 2.导出write public void export(HttpServletResponse response) {try {String f…...
flink源码编译-job提交
1、启动standalone集群的taskmanager standalone集群中的taskmanager启动类为 TaskManagerRunner 2 打开master启动类 通过 ctrln快捷键,找到、并打开类: org.apache.flink.runtime.taskexecutor.TaskManagerRunner 3 修改运⾏配置 基本完全按照mas…...
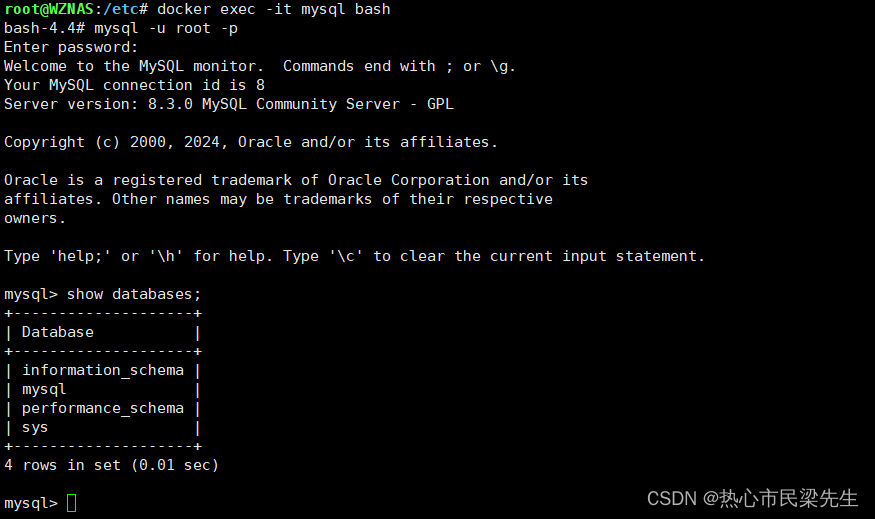
Mysql密码修改问题
docker安装mysql,直接拉取镜像,挂载关键目录即可启动,默认3306端口。此时无法直接连接,需要配置密码。docker进入mysql容器中 docker exec -it mysql bash #mysq是容器名称,也可以用容器id通过修改mysql的配置进行免密…...

建独立站,对FP商家有什么好处?
2024年都过去四分之一了,还有许多人对是否投身于跨境独立站领域仍犹豫不决。然而,观望不如实践,如果渴望在跨境电商领域开创一片新天地,那么现在就是行动的最佳时机。 特别是对于FP商家来说,由于电商平台对于黑五类产品…...
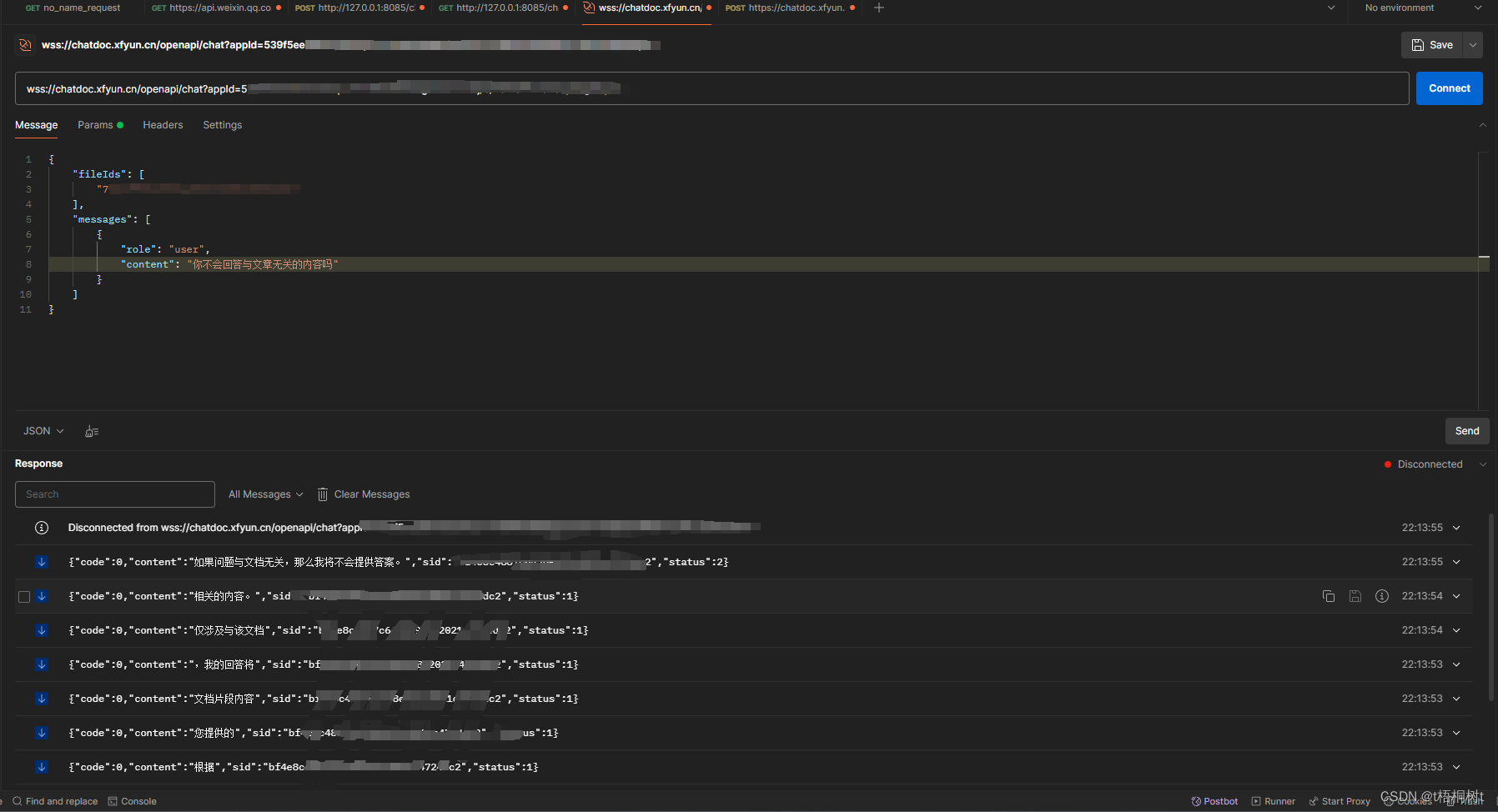
使用Postman进行websocket接口测试
因为最近要搞关于基于AI的文本接口测试.需要用到websocket协议,于是看了一下发现postman也可以测而且很方便 位置 File->New->WebSocket 可以看到不止WebSocket还支持其他的各种协议 使用 首先先点击connect进行连接 连接成功之后可以选择多种文本格式添加请求参数 每…...

Android音视频开发 - MediaMetadataRetriever 相关
Android音视频开发 - MediaMetadataRetriever 相关 MediaMetadataRetriever 是android中用于从媒体文件中提取元数据新的类. 可以获取音频,视频和图像文件的各种信息,如时长,标题,封面等. 1:初始化对象 private MediaMetadataRetriever mediaMetadataRetriever new MediaMe…...
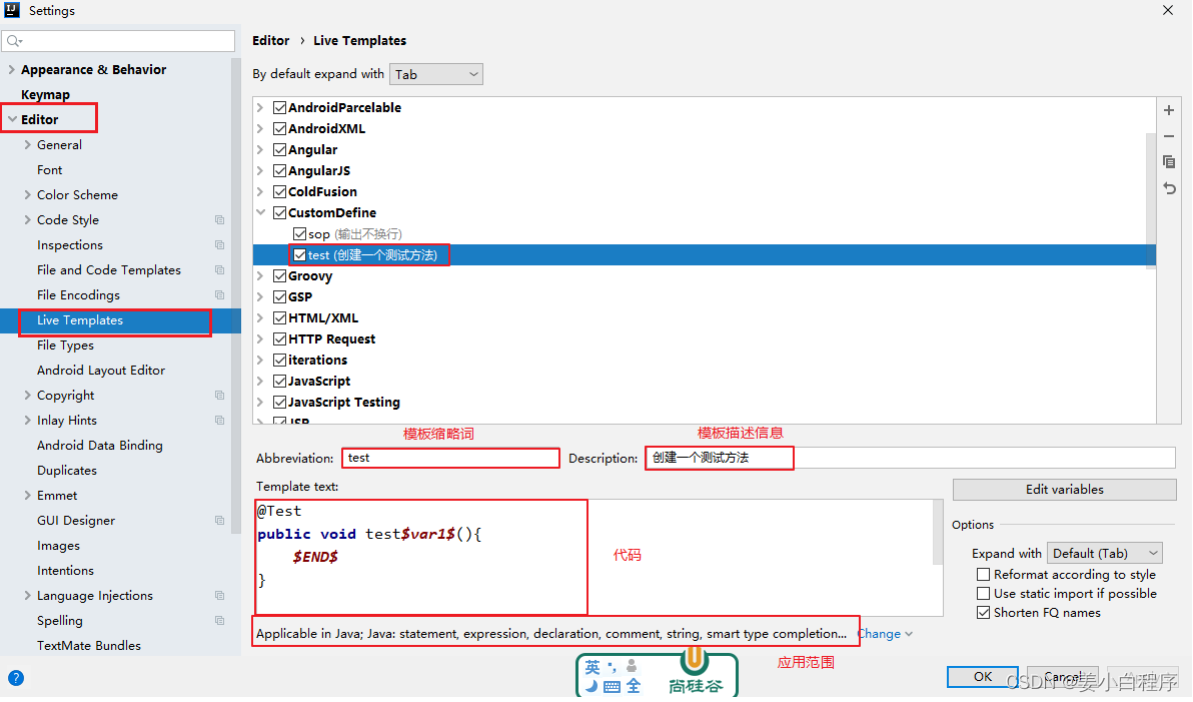
注解(Annotation)
10.1 注解概述 10.1.1 什么是注解 注解(Annotation)是从JDK5.0开始引入,以“注解名”在代码中存在。例如: Override Deprecated SuppressWarnings(value”unchecked”) Annotation 可以像修饰符一样被使用,可用于修饰…...

蓝桥杯:七步诗 ← bfs
【题目来源】https://www.lanqiao.cn/problems/3447/learning/【题目描述】 煮豆燃豆苴,豆在釜中泣。本是同根生,相煎何太急?---曹植 所以,这道题目关乎豆子! 话说赤壁之战结束后,曹操的船舰被刘备烧了,引领军队从华容…...

Vue 如何快速上手
目录 1. Vue 是什么 (概念) 1.1. Vue 的两种使用方式 1.2. 优点 1.3. 缺点 2. 创建 Vue 实例,初始化渲染 2.1. 步骤(核心步骤 4步) 2.2. 练习——创建一个Vue实例 3. 插值表达式 {{ }} 3.1. 介绍 3.2. 作用…...

Vue3:组件间通信-provide和inject实现祖先组件与后代组件间直接通信
一、情景说明 我们学习了很多的组件间通信 这里在学习一种,祖先组件与后代组件间通信的技术 这里的后代,可以是多层继承关系,子组件,子子组件,子子子组件等等。 在祖先组件中通过provide配置向后代组件提供数据在后代…...

微信小程序——小程序和页面生命周期详解
小程序的生命周期 小程序的生命周期主要分为以下几个阶段: 创建(onLoad): 当小程序启动时,或者从其他页面跳转到当前页面时,会触发 onLoad 生命周期函数。 这个阶段通常用于初始化页面数据,从服…...

android studio中添加module依赖
android常用的三种依赖 库依赖(Library dependency):以访问网址的形式将依赖库相应版本下载到本地; 文件依赖(File dependency): 将下载下来的依赖库以.jar文件的形式添加依赖. module依赖(Modu…...

【.NET全栈】.NET全栈学习路线
一、微软官方C#学习 https://learn.microsoft.com/zh-cn/dotnet/csharp/tour-of-csharp/ C#中的数据类型 二、2021 ASP.NET Core 开发者路线图 GitHub地址:https://github.com/MoienTajik/AspNetCore-Developer-Roadmap/blob/master/ReadMe.zh-Hans.md 三、路线…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
