【Python基础教程】5. 数

🎈个人主页:豌豆射手^
🎉欢迎 👍点赞✍评论⭐收藏
🤗收录专栏:python基础教程
🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进步!
专栏往期文章:
【Python基础教程】5. 数与表达式
- 一 数的概念
- 1.1 概念
- 1.2 类比
- 二、数的类型
- 2.1 整型(int)
- 2.2 浮点型(float)
- 2.3 复数(complex)
- 三、数值运算
- 3.1算术运算符
- 加(+)
- 减(-)
- 乘(*)
- 除(/)
- 取模(%)
- 幂运算(**)
- 整除(//)
- 3.2 运算符优先级与结合性
- 优先级顺序
- 结合性
- 四、类型转换
- 4.1 隐式类型转换
- 4.2 显式类型转换
- 总结

引言:
在Python编程的世界里,数是最基础、也是最重要的概念之一。
无论是进行简单的数学计算,还是构建复杂的算法,都离不开对数的操作和处理。
在本篇博客中,我们将深入探讨Python中数的概念、类型、运算以及类型转换,帮助大家更好地理解和运用Python中的数值处理。
首先,我们会介绍数的概念,并通过一些生动的类比来帮助大家理解。接着,我们将详细解析Python中的三种主要数的类型:整型、浮点型和复数,以及它们各自的特点和用法。
掌握了数的类型之后,我们将进入数值运算的讲解。我们将介绍Python中的基本算术运算符,包括加、减、乘、除、取模、幂运算和整除等,并解释它们的用法和运算规则。同时,我们还将讨论运算符的优先级和结合性,帮助大家避免常见的运算错误。
最后,我们将探讨类型转换的概念。在Python中,有时我们需要将一种类型的数转换为另一种类型,以便进行特定的运算或操作。我们将介绍隐式类型转换和显式类型转换的概念和用法,并举例说明它们在实际编程中的应用。
通过本篇博客的学习,相信大家对Python中的数值处理会有更深入的理解,为后续的编程学习打下坚实的基础。
一 数的概念
1.1 概念
在Python中,数(Numbers)是基本的数据类型,用于表示数值。Python支持多种数值类型,每种类型都有其特定的用途和特性。
数据类型(DataType)
它是计算机科学中的一个基本概念,它指的是在程序设计中用于定义变量或函数参数等所能存储数据的种类。在编程语言中,每种数据类型都有其特定的存储方式、取值范围以及可进行的操作。
数据类型的作用在于帮助程序员明确数据的性质,以便正确地使用这些数据,并优化数据的存储和运算效率。
在Python中,变量的数据类型是动态的,可以在程序运行过程中改变。这意味着程序员无需在声明变量时指定其数据类型,Python解释器会根据赋给变量的值自动推断其数据类型。这种动态类型系统使得Python编程更加灵活和便捷。
在现实生活中,我们可以将数据类型比作不同类型的容器,用于存储和表示不同类型的物品。这些容器具有不同的特性,决定了它们能装什么、不能装什么,以及如何使用和处理其中的物品。
Python中的数可以参与各种数学运算,如加法、减法、乘法、除法、取模等,并遵循一定的运算优先级和结合性。
Python还提供了丰富的数学函数和操作符来处理这些数,使得数值计算变得简单而高效。
在Python中,数值不仅可以用于基本的数学运算,还可以作为条件判断、循环控制、列表和元组等复合数据类型的元素,以及作为函数和方法的参数或返回值。因此,理解Python中数的概念对于掌握Python编程基础是非常重要的。
1.2 类比
在现实生活中,我们可以将Python中的数类比为日常生活中的各种“量”或“数值”。这些数值可以是整数、小数或表示某种特殊关系的数值(如复数),它们都有各自的实际意义和用途。
以一家超市为例:
-
整型:在超市中,我们经常会遇到整数,比如购买的商品数量、库存数量、货架编号等。这些整数都是精确且没有小数部分的,就像Python中的整型一样,用于表示完整、确切的数值。
-
浮点型:当涉及到商品的价格、重量或顾客的消费总额时,我们通常会使用带有小数点的数值。这些浮点数值能够更精确地表示实际情况,就像Python中的浮点型一样,用于处理需要小数精度的计算。
-
复数:虽然在日常超市购物中不太可能直接遇到复数,但我们可以将其类比为某种特殊情境下的数值表示。比如,在某些科学计算或工程应用中,可能需要用到复数以表示某种周期性变化或波动。这就像超市中某些特殊商品的促销策略,可能涉及复杂的计算模式,需要用到类似复数的概念来理解和处理。
通过这个类比,我们可以理解Python中的数是如何与现实世界中的数值相对应的。在Python编程中,我们可以使用这些数值类型来进行各种计算和操作,就像在现实生活中我们使用不同的数值来表示和处理各种情况一样。掌握这些数值类型的概念和用法,对于编写准确、高效的Python程序至关重要。
二、数的类型
具体介绍Python中数的类型如下:
2.1 整型(int)
定义与示例:
整型用于表示整数,即没有小数部分的数字。
在Python中,整型的范围取决于计算机的内存大小和使用的Python解释器。
示例:
# 创建一个整型变量
num_int = 10
print(num_int) # 输出: 10
print(type(num_int)) # 输出: <class 'int'>
进制转换(二进制、八进制、十六进制):
Python中整型支持多种进制数的表示。除了默认的十进制外,还可以使用前缀来表示其他进制:
- 二进制:以
0b或0B开头 - 八进制:以
0o或0O开头 - 十六进制:以
0x或0X开头
示例:
# 二进制数
binary_num = 0b1010 # 等价于十进制的10
print(binary_num) # 输出: 10# 八进制数
octal_num = 0o12 # 等价于十进制的10
print(octal_num) # 输出: 10# 十六进制数
hex_num = 0xA # 等价于十进制的10
print(hex_num) # 输出: 10
此外,还可以使用内置函数bin(), oct(), 和 hex() 将十进制数转换为相应的二进制、八进制和十六进制字符串表示形式。
函数
在Python中,函数是一段可重用的代码块,它执行特定的任务并可能返回结果。函数通过定义名称、参数和代码体来创建,可以多次调用以执行相同的操作,从而提高代码的可读性、可维护性和效率。
可以将Python中的函数想象成一家餐厅中的菜单项。每个菜单项(即函数)都对应着一道特定的菜品(即任务),有自己的名称(函数名)、所需的原料(参数)以及制作步骤(代码体)。
当顾客(即程序)想要品尝这道菜品时,只需向服务员(即代码调用者)点单,服务员便会按照菜单上的制作步骤为顾客准备这道菜。同样地,在程序中,我们可以通过调用函数来执行特定的任务,而无需每次都重新编写相同的代码。这样,不仅提高了代码的可读性和可维护性,还使得代码更加高效和简洁。
print函数
它是Python中的一个内置函数,它的主要功能是输出指定的信息到控制台,使得程序员能够直观地看到程序运行过程中的数据和结果。
2.2 浮点型(float)
定义与示例:
浮点型用于表示带有小数点的实数。在Python中,浮点数是双精度浮点数,使用64位来存储。
示例:
# 创建一个浮点型变量
num_float = 3.14
print(num_float) # 输出: 3.14
print(type(num_float)) # 输出: <class 'float'>
精度问题:
由于计算机内部表示浮点数的限制,有些浮点数可能不能精确表示,这会导致一些看似简单的数学运算产生不精确的结果。例如:
print(0.1 + 0.2) # 输出: 0.30000000000000004,而不是期望的0.3
这种精度问题在财务计算或需要高精度计算的场合尤为重要,通常需要使用专门的库(如decimal模块)来处理。
2.3 复数(complex)
定义与示例:
复数由实部和虚部组成,可以表示为a + bj,其中a是实部,b是虚部,j(或J)是虚数单位,满足j^2 = -1。
示例:
# 创建一个复数变量
num_complex = 3 + 4j
print(num_complex) # 输出: (3+4j)
print(type(num_complex)) # 输出: <class 'complex'>
type()函数
type函数在Python中扮演着重要角色,它的主要功能是用于获取对象的数据类型,帮助程序员了解对象的具体类型,以便在编程过程中进行更准确的类型判断和操作。在这里,num_complex就是一个对象。
实部与虚部:
可以通过real和imag属性分别访问复数的实部和虚部。
属性
在Python中,属性是对象的特性或数据,它描述了对象的某种状态或特征。属性可以通过点(.)操作符来访问和修改,是面向对象编程中不可或缺的一部分,使得对象能够具有更加丰富的描述和行为。
示例:
# 访问复数的实部和虚部
real_part = num_complex.real # 实部为3
imag_part = num_complex.imag # 虚部为4
print(real_part) # 输出: 3.0
print(imag_part) # 输出: 4.0
复数在Python中主要用于科学计算、信号处理、工程应用等领域,其中涉及到需要表示和处理波动、旋转等复杂数学概念的场合。通过内置的复数类型,Python可以方便地执行复数的算术运算。
三、数值运算
在Python中,数值运算主要通过算术运算符进行。这些运算符允许我们对数值类型的变量进行加法、减法、乘法、除法、取模、幂运算和整除等操作。下面是对这些运算符的具体介绍:
3.1算术运算符
加(+)
用于将两个数值相加。
a = 5
b = 3
result = a + b # 结果为 8
减(-)
用于从一个数值中减去另一个数值。
a = 5
b = 3
result = a - b # 结果为 2
乘(*)
用于将两个数值相乘。
a = 5
b = 3
result = a * b # 结果为 15
除(/)
用于将第一个数值除以第二个数值,返回浮点数结果。
a = 5
b = 2
result = a / b # 结果为 2.5
取模(%)
返回两数相除的余数。
a = 5
b = 2
result = a % b # 结果为 1
幂运算(**)
用于计算第一个数值的第二个数值次方。
a = 2
b = 3
result = a ** b # 结果为 8
整除(//)
返回商的整数部分,忽略小数部分。
a = 5
b = 2
result = a // b # 结果为 2
3.2 运算符优先级与结合性
优先级顺序
Python中的算术运算符具有不同的优先级,优先级从高到低如下:
- 括号
- 幂运算(**)
- 乘(*)、除(/)、整除(//)、取模(%)
- 加(+)、减(-)
优先级决定了在没有括号的情况下,算术表达式中各个部分如何计算。
例如,乘法和除法会先于加法和减法执行。
结合性
结合性是指当多个相同优先级的运算符出现在表达式中时,它们如何结合。在Python中,除了幂运算外,大多数算术运算符都是左结合的,这意味着它们从左到右进行计算。例如:
a = 2
b = 3
c = 4
result = a - b - c # 等价于 (a - b) - c,结果为 -5
然而,幂运算具有右结合性,意味着它会从右向左计算:
a = 2
b = 3
c = 2
result = a ** b ** c # 等价于 a ** (b ** c),结果为 512
理解运算符的优先级和结合性对于编写清晰且高效的代码至关重要,可以避免由于计算顺序错误而导致的逻辑问题。在复杂的表达式中,使用括号来明确指定计算顺序通常是一个好的编程习惯。
四、类型转换
在Python中,类型转换是一个重要的概念,它允许我们在不同的数据类型之间进行转换。下面将详细解释隐式类型转换和显式类型转换,并给出相应的示例。
4.1 隐式类型转换
隐式类型转换是Python在运行时自动进行的数据类型转换,程序员通常不需要显式地指定。Python会根据上下文的需要自动进行这种转换。
示例说明:
当我们进行数学运算时,Python会尝试自动转换数据类型以确保运算可以正确进行。
# 整数与浮点数相加,整数自动转换为浮点数
a = 5
b = 3.0
result = a + b # result的值为8.0,整数a自动转换为浮点数# 字符串与整数相加,引发TypeError,因为字符串和整数之间不能自动转换
c = "5"
d = 3
# e = c + d # 这行会报错,TypeError: can only concatenate str (not "int") to str# 正确的方式是将整数转换为字符串
e = c + str(d) # e的值为"53"
在这个例子中,当整数a与浮点数b相加时,Python自动将整数a转换为浮点数以完成运算。然而,字符串与整数相加时,由于它们之间不存在自然的隐式转换规则,所以Python会抛出一个TypeError异常。
4.2 显式类型转换
显式类型转换是指程序员通过调用内置函数(如int()、float()、complex()等)来明确地将一个数据类型转换为另一个数据类型。
函数的使用:
int(): 将一个数值或字符串转换为整数。float(): 将一个数值或字符串转换为浮点数。complex(): 创建一个复数。
示例:
# 将浮点数转换为整数
x = 3.14
int_x = int(x) # int_x的值为3,小数部分被丢弃# 将字符串转换为整数
str_y = "42"
int_y = int(str_y) # int_y的值为整数42# 将整数转换为浮点数
z = 7
float_z = float(z) # float_z的值为7.0# 将字符串转换为浮点数
str_w = "3.14"
float_w = float(str_w) # float_w的值为浮点数3.14# 创建复数
complex_num = complex(3, 4) # complex_num的值为3+4j
注意事项:
- 当使用
int()函数转换浮点数时,小数部分会被丢弃,不进行四舍五入。 - 使用
int()或float()转换字符串时,字符串必须表示一个有效的数字,否则会抛出ValueError。 complex()函数接收两个参数,第一个参数为实部,第二个参数为虚部。
错误处理的示例:
try:# 尝试将一个非数字字符串转换为整数invalid_str = "abc"int_invalid = int(invalid_str) # 这会抛出ValueError
except ValueError as e:print(f"转换错误: {e}") # 输出错误信息
在这个错误处理的示例中,我们尝试将一个非数字字符串"abc"转换为整数,这会引发ValueError异常。我们使用try-except块来捕获这个异常,并打印出错误信息。
总结
通过本篇博客的学习,我们全面了解了Python中数的概念、类型、运算以及类型转换。我们深入探讨了整型、浮点型和复数这三种主要的数的类型,并学习了如何使用它们进行各种数值运算。同时,我们也掌握了运算符的优先级和结合性,以避免在复杂的运算中出现错误。
此外,我们还介绍了类型转换的概念和用法,包括隐式类型转换和显式类型转换。了解这些转换方法可以帮助我们在编程中更加灵活地处理各种数值类型,实现更复杂的逻辑和功能。
总的来说,本篇博客为大家提供了一个全面而深入的Python数值处理教程,希望能够帮助大家更好地掌握Python编程中的数值处理技巧,为后续的编程学习和实践打下坚实的基础。
相关文章:

【Python基础教程】5. 数
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:python基础教程 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、…...
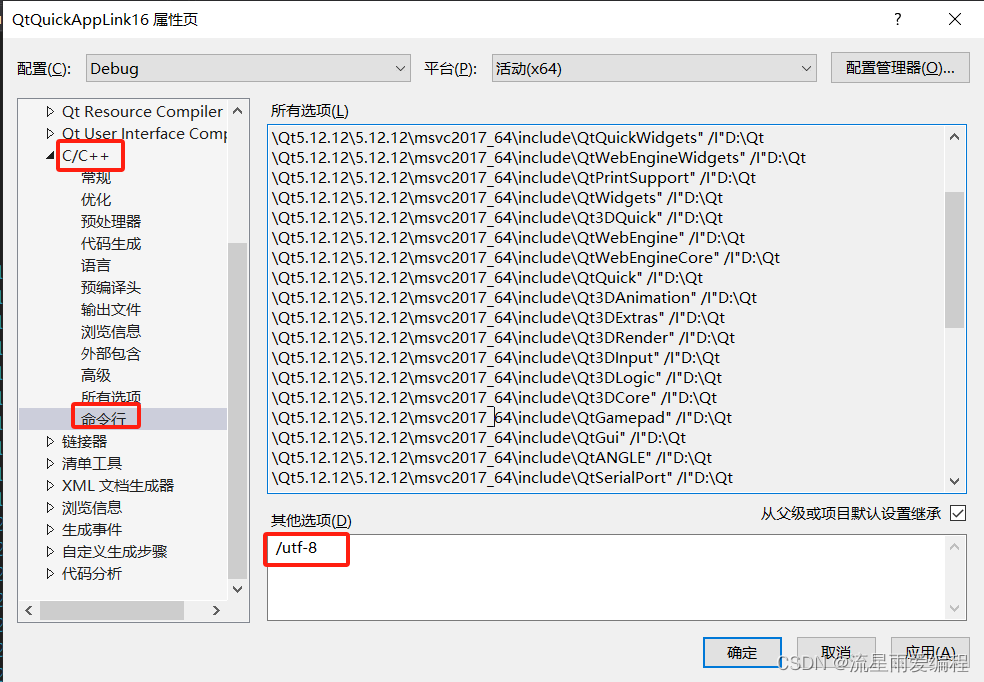
Qt中出现中文乱码的原因以及解决方法
Qt专栏:http://t.csdnimg.cn/C2SDN 目录 1.引言 2.原因分析 3.源文件的编码格式修改方法 4.程序内部使用的默认编码格式修改方法 5.QString转std::string的方法 6.总结 1.引言 在编写Qt程序的时候,或多或少都可能遇到用QString时候,明明…...

Linux 文件相关命令
一、查看文件命令 1)浏览文件less 默认查看文件的前 10 行。 less /etc/services ##功能说明: #1.默认打开首屏内容 #2.按【回车】按行访问 #3.按【空格】按屏访问 #4.【从上向下】搜索用/111,搜索包含111的内容,此时按n继续向下搜&#x…...

K8S Deployment 简介, 1个简单的Kubernetes Deployment YAML 文件
当谈到 Kubernetes 集群中的应用程序部署和管理时,Deployment、ReplicaSet 和 Pod 是三个重要的概念。它们之间存在一定的关系和层次结构。下面是对 Deployment、ReplicaSet 和 Pod 的详细解释以及它们之间的关系。 Deployment(部署) Deploy…...
win11安装WSL UbuntuTLS
win11安装WSL WSL 简介WSL 1 VS WSL 2先决要求安装方法一键安装通过「控制面板」安装 WSL 基本命令Linux发行版安装Ubuntu初始化相关设置root用户密码网络工具安装安装1panel面板指导 WSl可视化工具问题总结WSL更新命令错误Ubuntu 启动初始化错误未解决问题 WSL 简介 Windows …...

第十题:金币
题目描述 国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到…...

Windows 11 中Docker的安装教程
选择正确的Docker版本 在Windows上,你可以安装两种类型的Docker:Docker Desktop和Docker Toolbox。Docker Desktop是针对Windows 10 Pro、Enterprise和Education版本的,这些版本内置了Hyper-V虚拟化支持。对于旧版本的Windows,比…...
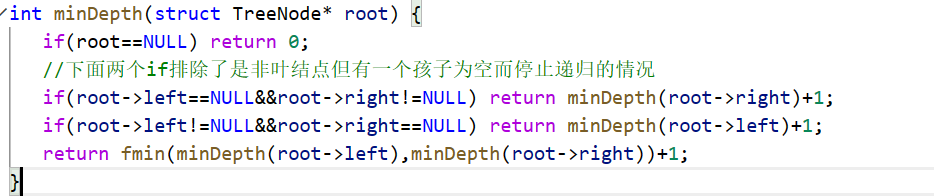
纯C代码模板
一、快排 void QuickSort(int *a,int left,int right){if(left>right) return;else{int low left,high right;int pivot a[low];while(low<high){while(a[high] > pivot && low < high){high--;}a[low] a[high]; //必须先动a[low]while(a[low] < …...
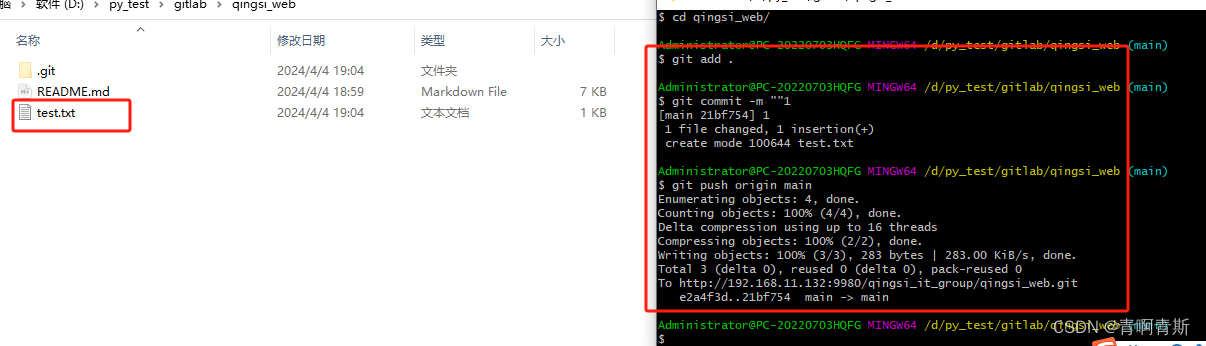
二、GitLab相关操作
GitLab相关操作 一、组、用户、项目管理1.创建组2.创建项目3.创建用户并分配组3.1 创建用户3.2 设置密码3.3 给用户分配组 二、拉取/推送代码1.配置ssh(第一次需要)1.1 创建一个空文件夹1.2 配置本地仓账号和邮箱1.3 生成ssh公钥密钥1.4 gitlab配置公钥 2.拉取代码3.推送代码3.…...

【详细注释+流程讲解】基于深度学习的文本分类 TextCNN
前言 这篇文章用于记录阿里天池 NLP 入门赛,详细讲解了整个数据处理流程,以及如何从零构建一个模型,适合新手入门。 赛题以新闻数据为赛题数据,数据集报名后可见并可下载。赛题数据为新闻文本,并按照字符级别进行匿名…...

Day.21
interface MyInterface{public final static int PI 3;void show();public default void printX(){System.out.println("接口默认方法");}public static void printY(){System.out.println("接口静态方法");}}class MyClass implements MyInterface{publi…...

Spring-IoC 基于注解
基于xml方法见:http://t.csdnimg.cn/dir8j 注解是代码中的一种特殊标记,可以在编译、类加载和运行时被读取,执行相应的处理,简化 Spring的 XML配置。 格式:注解(属性1"属性值1",...) 可以加在类上…...
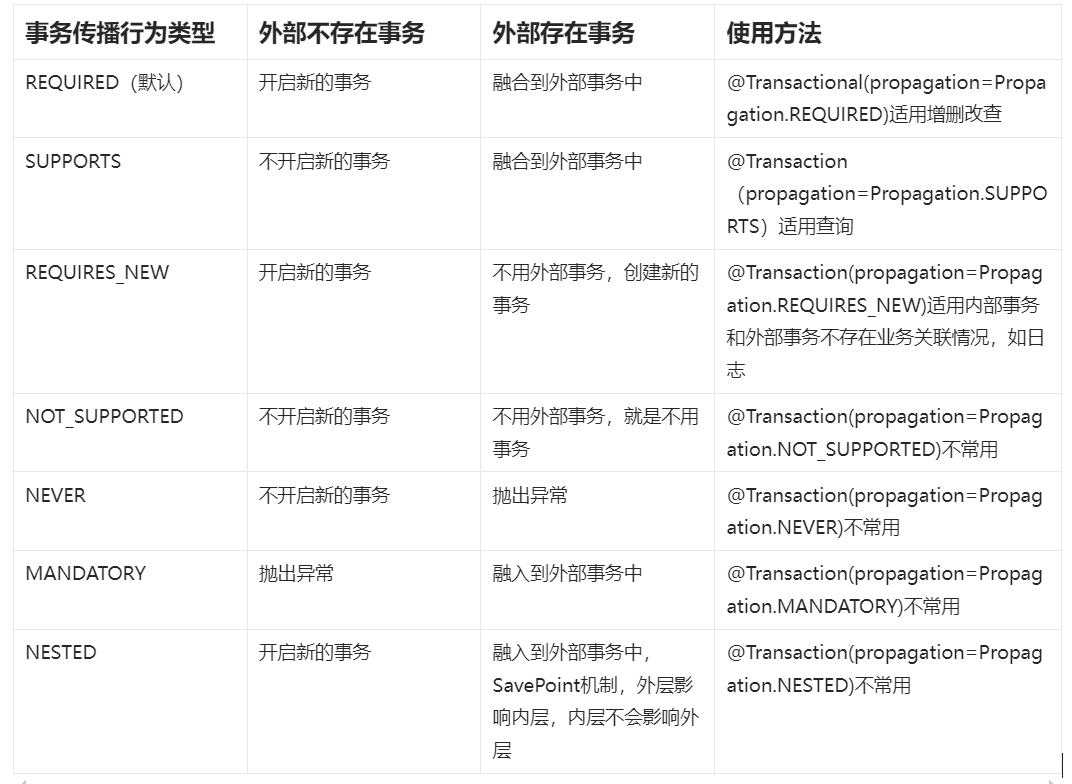
Spring声明式事务以及事务传播行为
Spring声明式事务以及事务传播行为 Spring声明式事务1.编程式事务2.使用AOP改造编程式事务3.Spring声明式事务 事务传播行为 如果对数据库事务不太熟悉,可以阅读上一篇博客简单回顾一下:MySQL事务以及并发访问隔离级别 Spring声明式事务 事务一般添加到…...

【C语言数据库】Sqlite3基础介绍
1. SQLite简介 SQLite is a C-language library that implements a small, fast, self-contained, high-reliability, full-featured, SQL database engine. SQLite is the most used database engine in the world. SQLite is built into all mobile phones and most computer…...
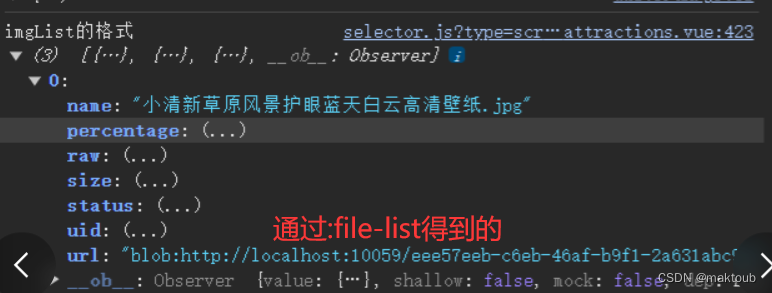
el-upload上传图片图片、el-load默认图片重新上传、el-upload初始化图片、el-upload编辑时回显图片
问题 我用el-upload上传图片,再上一篇文章已经解决了,el-upload上传图片给SpringBoot后端,但是又发现了新的问题,果然bug是一个个的冒出来的。新的问题是el-upload编辑时回显图片的保存。 问题描述:回显图片需要将默认的 file-lis…...
【拓扑空间】示例及详解1
例1 度量空间的任意两球形邻域的交集是若干球形邻域的并集 Proof: 任取空间的两个球形邻域、,令 任取,令 球形领域 例2 规定X的子集族,证明是X上的一个拓扑 Proof: 1. 2., (若干个球形邻域的并集都是的元素,元素…...

linux安装jdk8
上传到某个目录,例如:/usr/local/ tar -xvf jdk-8u144-linux-x64.tar.gz配置环境变量: export JAVA_HOME/usr/local/java export PATH$PATH:$JAVA_HOME/bin设置环境变量: source /etc/profile...
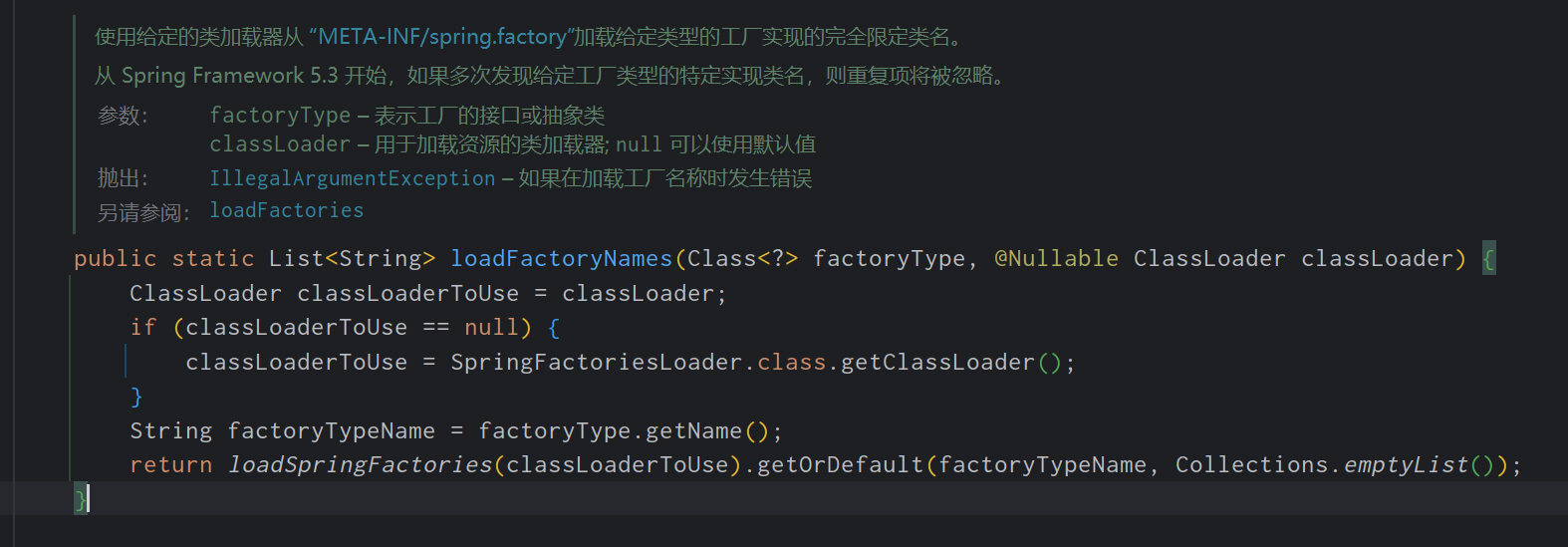
Spring重点知识(个人整理笔记)
目录 1. 为什么要使用 spring? 2. 解释一下什么是 Aop? 3. AOP有哪些实现方式? 4. Spring AOP的实现原理 5. JDK动态代理和CGLIB动态代理的区别? 6. 解释一下什么是 ioc? 7. spring 有哪些主要模块?…...

HTML基础知识详解(上)(如何想知道html的全部基础知识点,那么只看这一篇就足够了!)
前言:在学习前端基础时,必不可少的就是三大件(html、css、javascript ),而HTML(超文本标记语言——HyperText Markup Language)是构成 Web 世界的一砖一瓦,它定义了网页内容的含义和…...

如何借助Idea创建多模块的SpringBoot项目
目录 1.1、前言1.2、开发环境1.3、项目多模块结构1.4、新建父工程1.5、创建子模块1.6、编辑父工程的pom.xml文件 1.1、前言 springmvc项目,一般会把项目分成多个包:controler、service、dao、utl等,但是随着项目的复杂性提高,想复用其他一个模…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
