当前位置： 首页 > news >正文

11. 瀑布流布局

news 2026/2/8 13:57:52 
<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><meta name="viewport" content="width=device-width, initial-scale=1.0" /><title>11.瀑布流布局</title><style>#container {position: relative;}img {position: absolute;}</style></head><body><div id="container"></div></body><script>var divContainer = document.getElementById('container')var imgWidth = 220 //每张图片的固定宽度//1. 加入图片元素function createImgs() {for (var i = 0; i <= 40; i++) {var height = Math.ceil(Math.random() * 100 + 200)var src = 'https://picsum.photos/220/' + height //生成图片的src路径var img = document.createElement('img')img.onload = setPoisionsimg.src = src //设置src路径divContainer.appendChild(img) //添加到容器中}}createImgs()// 2. 设置每张图片的位置function setPoisions() {/*** 计算一共有多少列，以及每一列之间的间隙*/function cal() {var containerWidth = divContainer.clientWidth //容器的宽度//计算列的数量var columns = Math.floor(containerWidth / imgWidth)//计算间隙var spaceNumber = columns + 1 //间隙数量var leftSpace = containerWidth - columns * imgWidth //计算剩余的空间var space = leftSpace / spaceNumber //每个间隙的空间return {space: space,columns: columns,}}var info = cal() //得到列数，和 间隙的空间var nextTops = new Array(info.columns) //该数组的长度为列数，每一项表示该列的下一个图片的纵坐标nextTops.fill(0) //将数组的每一项填充为0for (var i = 0; i < divContainer.children.length; i++) {var img = divContainer.children[i]//找到nextTops中的最小值作为当前图片的纵坐标var minTop = Math.min.apply(null, nextTops)img.style.top = minTop + 'px'//重新设置数组这一项的下一个top值var index = nextTops.indexOf(minTop) //得到使用的是第几列的top值nextTops[index] += img.height + info.space//横坐标var left = (index + 1) * info.space + index * imgWidthimg.style.left = left + 'px'}var max = Math.max.apply(null, nextTops) //求最大值divContainer.style.height = max + 'px' //3. 设置容器的高度}var timerId = null //一个计时器的idwindow.onresize = function () {//窗口尺寸变动后，重新排列if (timerId) {clearTimeout(timerId)}timerId = setTimeout(setPoisions, 300)}</script>
</html>

相关文章：

11. 瀑布流布局

<!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8" /><meta name"viewport" content"widthdevice-width, initial-scale1.0" /><title>11.瀑布流布局</title><style>#cont…...

编程日记 2024/4/5 21:35:39

Flutter-发布插件到pub上传不上问题

问题1&#xff1a; 尝试指令&#xff1a; flutter packages pub publish --serverhttps://pub.dartlang.org问题2&#xff1a; 问题1解决后&#xff0c;进入验证身份&#xff0c;点击终端显示的链接&#xff0c;跳转到google验证&#xff0c;记得这里要科*学上网&#xff0c;点…...

编程日记 2024/4/5 21:34:38

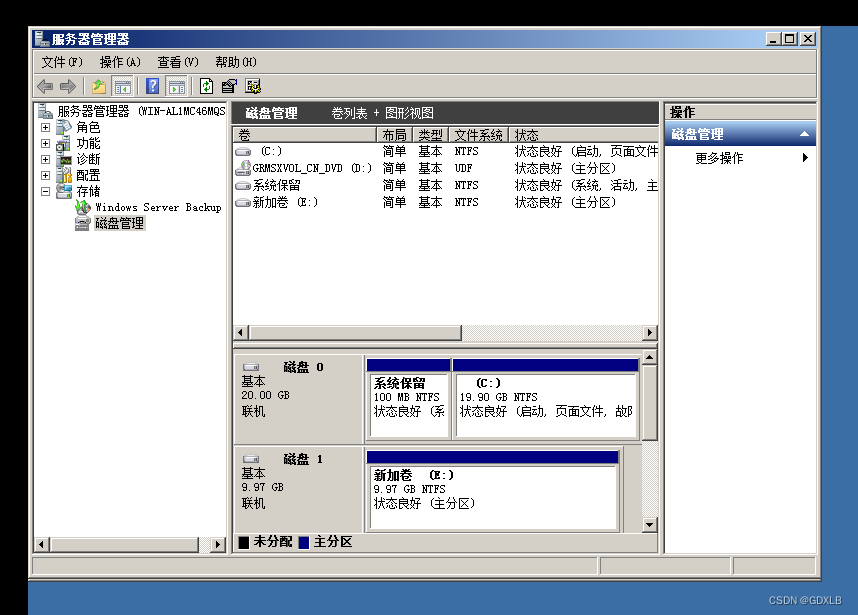
Windows 2008虚拟机安装、安装VM Tools、快照和链接克隆、添加硬盘修改格式为GPT

一、安装vmware workstation软件 VMware workstation的安装介质&#xff0c;获取路径&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1AUAw_--yjZAUPbsR7StOJQ 提取码&#xff1a;umz1 所在目录&#xff1a;\vmware\VMware workstation 15.1.0 1.找到百度网盘中vmwa…...

编程日记 2024/4/5 21:30:34

c++的学习之路：12、vector（1）

这章主要是根据cplusplus中的文档进行使用Vector&#xff0c;文章末附上测试代码。 目录 一、什么是vector 二、vector的简单使用 三、代码 一、什么是vector 下图是cplusplus的简介&#xff0c;上面一共有六点&#xff0c;如下&#xff1a; 1、vector是表示可变大小数组…...

编程日记 2024/4/5 21:29:33

2024.2.17力扣每日一题——N叉树的层序遍历

2024.2.17 题目来源我的题解方法一 广度优先搜索&#xff08;队列实现&#xff09; 题目来源 力扣每日一题&#xff1b;题序&#xff1a;429 我的题解 方法一 广度优先搜索&#xff08;队列实现&#xff09; 和二叉树的层序遍历相同&#xff0c;只是在添加子节点的细节有所不…...

编程日记 2024/4/5 21:28:32

滑动窗口（尺取法/Python）

滑动窗口&#xff08;尺取法&#xff09; 算法含义&#xff1a; 在解决关于区间特性的题目时保存搜索区间左右端点&#xff0c;然后根据实际要求不断更新左右端点位置的算法 时间复杂度&#xff1a; O ( n ) O(n) O(n) 空间复杂度&#xff1a; O ( 1 ) O(1) O(1) 在历年真题…...

编程日记 2024/4/5 21:23:26

【打印SQL执行日志】⭐️Mybatis-Plus通过配置在控制台打印执行日志

目录 前言 一、Mybatis-Plus 开启日志的方式 二、测试 三、日志分析 章末 前言 小伙伴们大家好&#xff0c;相信大家平时在处理问题时都有各自的方式&#xff0c;最常用以及最好用的感觉还是断点调试&#xff0c;但是涉及到操作数据库的执行时&#xff0c;默认的话在控制台…...

编程日记 2024/4/5 21:13:19

Vue后台管理系统常用组件的优缺点分析

以下是Vue后台管理系统常用组件的优缺点分析&#xff1a; Element UI 优点&#xff1a; 丰富的组件库&#xff1a;Element UI 提供了大量的组件&#xff0c;包括表单、表格、弹窗、导航等&#xff0c;可以满足各种后台管理系统的需求。易于使用&#xff1a;Element UI 的组件…...

编程日记 2024/4/5 21:10:16

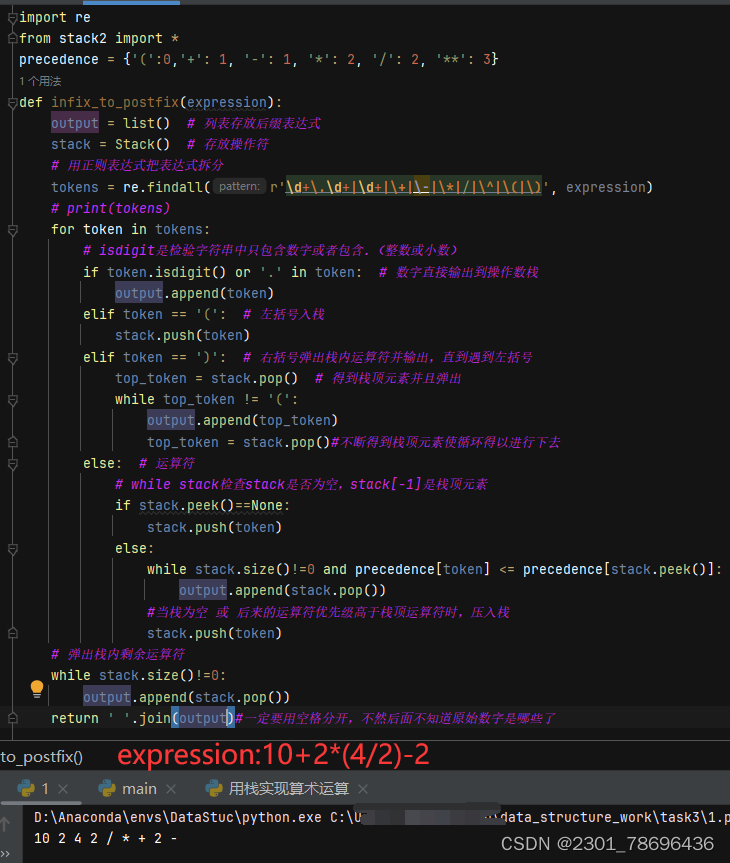
栈的应用——用栈实现算数混合运算表达式的计算

1、单目运算符双目运算符 算数运算符分为单目运算符和双目运算符等 单目运算符只需要一个操作数，双目运算符需要两个操作数 双目运算符最常见：常见的算术运算符：*/，比较运算符：<>=等等以下是一些单目运算符:正号 (+): 用于表示正数或给数值一个正号。例如：+5 仍然…...

编程日记 2024/4/5 21:02:09

动态规划—机器人移动问题（Java）

&#x1f600;前言 机器人移动问题是一个经典的动态规划应用场景&#xff0c;它涉及到在给定范围内的位置上进行移动&#xff0c;并计算到达目标位置的方法数。本文将介绍三种解决这一问题的方法&#xff1a;暴力递归、缓存法和动态规划。通过比较不同方法的优缺点&#xff0c;…...

编程日记 2024/4/5 20:59:06

第十一届蓝桥杯物联网试题（省赛）

对于通信方面&#xff0c;还是终端A、B都保持接收状态&#xff0c;当要发送的数组不为空再发送数据&#xff0c;发送完后立即清除&#xff0c;接收数据的数组不为空则处理&#xff0c;处理完后立即清除&#xff0c;分工明确 继电器不亮一般可能是电压不够 将数据加空格再加\r…...

编程日记 2024/4/5 20:58:04

【Python基础教程】5. 数

&#x1f388;个人主页&#xff1a;豌豆射手^ &#x1f389;欢迎 &#x1f44d;点赞✍评论⭐收藏 &#x1f917;收录专栏&#xff1a;python基础教程 &#x1f91d;希望本文对您有所裨益&#xff0c;如有不足之处&#xff0c;欢迎在评论区提出指正&#xff0c;让我们共同学习、…...

编程日记 2024/4/5 20:55:02

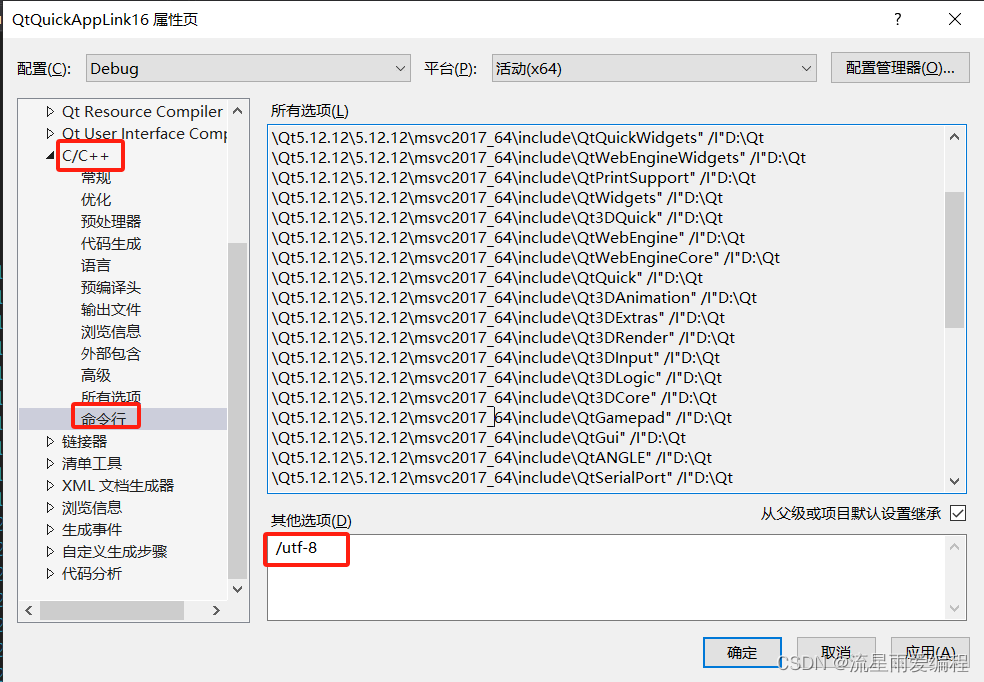
Qt中出现中文乱码的原因以及解决方法

Qt专栏&#xff1a;http://t.csdnimg.cn/C2SDN 目录 1.引言 2.原因分析 3.源文件的编码格式修改方法 4.程序内部使用的默认编码格式修改方法 5.QString转std::string的方法 6.总结 1.引言 在编写Qt程序的时候&#xff0c;或多或少都可能遇到用QString时候&#xff0c;明明…...

编程日记 2024/4/5 20:54:01

Linux 文件相关命令

一、查看文件命令 1&#xff09;浏览文件less 默认查看文件的前 10 行。 less /etc/services ##功能说明&#xff1a; #1.默认打开首屏内容 #2.按【回车】按行访问 #3.按【空格】按屏访问 #4.【从上向下】搜索用/111,搜索包含111的内容&#xff0c;此时按n继续向下搜&#x…...

编程日记 2024/4/5 20:52:59

K8S Deployment 简介， 1个简单的Kubernetes Deployment YAML 文件

当谈到 Kubernetes 集群中的应用程序部署和管理时&#xff0c;Deployment、ReplicaSet 和 Pod 是三个重要的概念。它们之间存在一定的关系和层次结构。下面是对 Deployment、ReplicaSet 和 Pod 的详细解释以及它们之间的关系。 Deployment&#xff08;部署&#xff09; Deploy…...

编程日记 2024/4/5 20:51:58

win11安装WSL UbuntuTLS

win11安装WSL WSL 简介WSL 1 VS WSL 2先决要求安装方法一键安装通过「控制面板」安装 WSL 基本命令Linux发行版安装Ubuntu初始化相关设置root用户密码网络工具安装安装1panel面板指导 WSl可视化工具问题总结WSL更新命令错误Ubuntu 启动初始化错误未解决问题 WSL 简介 Windows …...

编程日记 2024/4/5 20:49:56

第十题：金币

题目描述 国王将金币作为工资&#xff0c;发放给忠诚的骑士。第一天&#xff0c;骑士收到一枚金币&#xff1b;之后两天&#xff08;第二天和第三天&#xff09;&#xff0c;每天收到两枚金币&#xff1b;之后三天&#xff08;第四、五、六天&#xff09;&#xff0c;每天收到…...

编程日记 2024/4/5 20:46:53

Windows 11 中Docker的安装教程

选择正确的Docker版本 在Windows上&#xff0c;你可以安装两种类型的Docker&#xff1a;Docker Desktop和Docker Toolbox。Docker Desktop是针对Windows 10 Pro、Enterprise和Education版本的&#xff0c;这些版本内置了Hyper-V虚拟化支持。对于旧版本的Windows&#xff0c;比…...

编程日记 2024/4/5 20:45:51

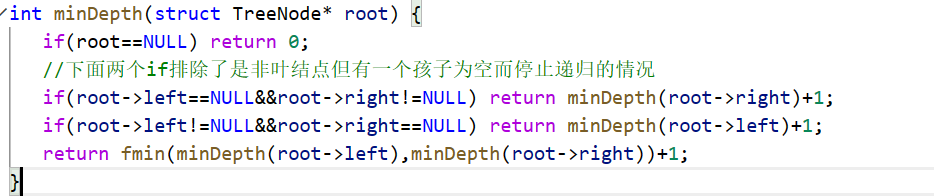
纯C代码模板

一、快排 void QuickSort(int *a,int left,int right){if(left>right) return;else{int low left,high right;int pivot a[low];while(low<high){while(a[high] > pivot && low < high){high--;}a[low] a[high]; //必须先动a[low]while(a[low] < …...

编程日记 2024/4/5 20:44:50

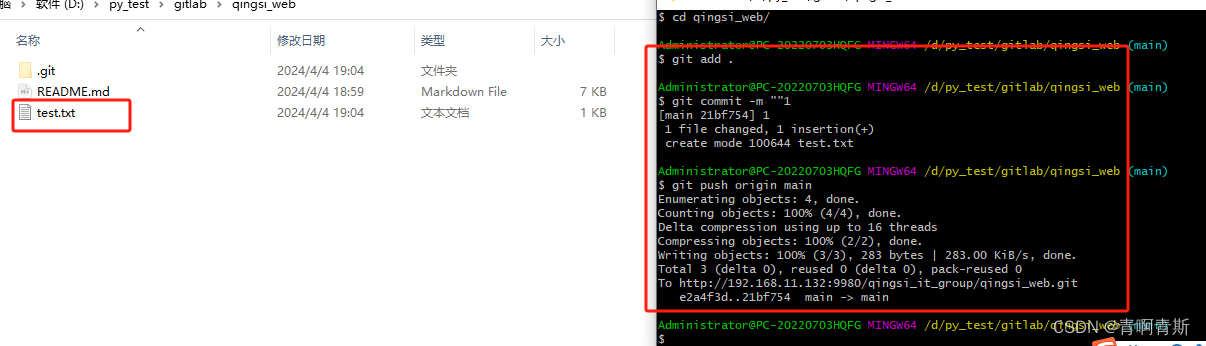
二、GitLab相关操作

GitLab相关操作 一、组、用户、项目管理1.创建组2.创建项目3.创建用户并分配组3.1 创建用户3.2 设置密码3.3 给用户分配组 二、拉取/推送代码1.配置ssh(第一次需要)1.1 创建一个空文件夹1.2 配置本地仓账号和邮箱1.3 生成ssh公钥密钥1.4 gitlab配置公钥 2.拉取代码3.推送代码3.…...

编程日记 2024/4/5 20:43:49

基于FPGA的PID算法学习———实现PID比例控制算法

基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容&#xff1a;参考网站&#xff1a; PID算法控制 PID即&#xff1a;Proportional&#xff08;比例&#xff09;、Integral&#xff08;积分&…...

编程新知 2026/2/6 17:50:11

【OSG学习笔记】Day 18: 碰撞检测与物理交互

物理引擎&#xff08;Physics Engine&#xff09; 物理引擎 是一种通过计算机模拟物理规律&#xff08;如力学、碰撞、重力、流体动力学等&#xff09;的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互&#xff0c;广泛应用于 游戏开发、动画制作、虚…...

编程新知 2026/2/4 2:08:30

Appium+python自动化（十六）- ADB命令

简介 Android 调试桥(adb)是多种用途的工具&#xff0c;该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具&#xff0c;其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利&#xff0c;如安装和调试…...

编程新知 2026/1/21 18:20:51

23-Oracle 23 ai 区块链表（Blockchain Table）

小伙伴有没有在金融强合规的领域中遇见&#xff0c;必须要保持数据不可变&#xff0c;管理员都无法修改和留痕的要求。比如医疗的电子病历中&#xff0c;影像检查检验结果不可篡改行的&#xff0c;药品追溯过程中数据只可插入无法删除的特性需求&#xff1b;登录日志、修改日志…...

编程新知 2026/1/27 3:40:30

ServerTrust 并非唯一

NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

编程新知 2026/1/29 5:29:57

如何在最短时间内提升打ctf（web)的水平？

刚刚刷完2遍 bugku 的 web 题&#xff0c;前来答题。 每个人对刷题理解是不同&#xff0c;有的人是看了writeup就等于刷了&#xff0c;有的人是收藏了writeup就等于刷了&#xff0c;有的人是跟着writeup做了一遍就等于刷了&#xff0c;还有的人是独立思考做了一遍就等于刷了。…...

编程新知 2026/1/28 5:55:15

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇&#xff0c;相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程&#xff0c;其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线&#xff0c; n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2026/1/30 4:47:24

Angular微前端架构：Module Federation + ngx-build-plus (Webpack)

以下是一个完整的 Angular 微前端示例&#xff0c;其中使用的是 Module Federation 和 npx-build-plus 实现了主应用&#xff08;Shell&#xff09;与子应用&#xff08;Remote&#xff09;的集成。 &#x1f6e0;️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

编程新知 2025/12/3 10:52:37

使用LangGraph和LangSmith构建多智能体人工智能系统

现在&#xff0c;通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战&#xff0c;比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

编程新知 2026/1/26 13:48:59

Selenium常用函数介绍

目录 一&#xff0c;元素定位 1.1 cssSeector 1.2 xpath 二&#xff0c;操作测试对象 三&#xff0c;窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四&#xff0c;弹窗 五&#xff0c;等待 六&#xff0c;导航 七&#xff0c;文件上传 …...

编程新知 2026/1/29 3:55:23