矩阵空间秩1矩阵小世界图
文章目录
- 1. 矩阵空间
- 2. 微分方程
- 3. 秩为1的矩阵
- 4. 图
1. 矩阵空间
我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。
- 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间
- 上三角矩阵-子空间-有6个3X3的上三角矩阵,所以为6维矩阵空间
矩阵M的基础基有9个,表示如下
[ 1 0 0 0 0 0 0 0 0 ] ; [ 0 1 0 0 0 0 0 0 0 ] ; [ 0 0 1 0 0 0 0 0 0 ] ; [ 0 0 0 1 0 0 0 0 0 ] ; (1) \begin{bmatrix}1&0&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&1&0\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&1\\\\0&0&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\1&0&0\\\\0&0&0\\\\\end{bmatrix};\tag{1} 100000000 ; 000100000 ; 000000100 ; 010000000 ;(1)
[ 0 0 0 0 1 0 0 0 0 ] ; [ 0 0 0 0 0 1 0 0 0 ] ; [ 0 0 0 0 0 0 1 0 0 ] ; [ 0 0 0 0 0 0 0 1 0 ] ; [ 0 0 0 0 0 0 0 0 1 ] ; (2) \begin{bmatrix}0&0&0\\\\0&1&0\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&1\\\\0&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\1&0&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&1&0\\\\\end{bmatrix};\begin{bmatrix}0&0&0\\\\0&0&0\\\\0&0&1\\\\\end{bmatrix};\tag{2} 000010000 ; 000000010 ; 001000000 ; 000001000 ; 000000001 ;(2)
2. 微分方程
- 假设我们有如下微分方程:
d 2 y d x 2 + y = 0 (3) \frac{\mathrm{d}^2y}{\mathrm{d}x^2}+y=0\tag{3} dx2d2y+y=0(3) - 零空间解表示如下:
y 1 = sin ( x ) ; y 2 = cos ( x ) (4) y_1=\sin(x);y_2=\cos(x)\tag{4} y1=sin(x);y2=cos(x)(4) - 通解表示如下:
y = c 1 sin ( x ) + c 2 cos ( x ) (5) y=c_1\sin(x)+c_2\cos(x)\tag{5} y=c1sin(x)+c2cos(x)(5)
以上可以用 sin ( x ) \sin(x) sin(x)和 cos ( x ) \cos(x) cos(x)当做解来表示解空间,所以微分方程的解空间为2.
3. 秩为1的矩阵
假设我们有一个秩为1的矩阵A ,表示如下:
A = [ 1 4 5 2 8 10 ] = [ 1 2 ] 2 × 1 [ 1 4 5 ] 1 × 3 (6) A=\begin{bmatrix}1&4&5\\\\2&8&10\end{bmatrix}=\begin{bmatrix}1\\\\2\end{bmatrix}_{2\times1}\begin{bmatrix}1&4&5\end{bmatrix}_{1\times3}\tag{6} A= 1248510 = 12 2×1[145]1×3(6)
- 所有的秩为1的矩阵均可以分解为列向量乘以行向量。
- 小结:
我们可以通过组合秩为1的矩阵来构造我们想要的秩的矩阵。
4. 图
我们知道一个图可以有节点和边组成
G r a p h = [ n o d e s , e d g e s ] (7) Graph=[nodes,edges]\tag{7} Graph=[nodes,edges](7)

相关文章:

矩阵空间秩1矩阵小世界图
文章目录 1. 矩阵空间2. 微分方程3. 秩为1的矩阵4. 图 1. 矩阵空间 我们以3X3的矩阵空间 M 为例来说明相关情况。目前矩阵空间M中只关心两类计算,矩阵加法和矩阵数乘。 对称矩阵-子空间-有6个3X3的对称矩阵,所以为6维矩阵空间上三角矩阵-子空间-有6个3…...
《QT实用小工具·十三》FlatUI辅助类之各种炫酷的控件集合
1、概述 源码放在文章末尾 FlatUI辅助类之各种炫酷的控件集合 按钮样式设置。文本框样式设置。进度条样式。滑块条样式。单选框样式。滚动条样式。可自由设置对象的高度宽度大小等。自带默认参数值。 下面是demo演示: 项目部分代码如下所示: #ifnd…...
dm8 备份与恢复
dm8 备份与恢复 基础环境 操作系统:Red Hat Enterprise Linux Server release 7.9 (Maipo) 数据库版本:DM Database Server 64 V8 架构:单实例1 设置bak_path路径 --创建备份文件存放目录 su - dmdba mkdir -p /dm8/backup--修改dm.ini 文件…...
Vue项目中引入html页面(vue.js中引入echarts数据大屏html [静态非数据传递!] )
在项目原有vue(例如首页)基础上引入html页面 1、存放位置 vue3原有public文件夹下 我这边是新建一个static文件夹 专门存放要用到的html文件 复制拖拽过来 index为html的首页 2、更改路径引入到vue中 这里用到的是 iframe 方法 不同于vue的 component…...

ASTM C1186-22 纤维水泥平板
以无石棉类无机矿物纤维、有机合成纤维或纤维素纤维,单独或混合作为增强材料,以普通硅酸盐水泥或水泥中添加硅质、钙质材料代替部分水泥为胶凝材料,经制浆、成型、蒸汽或高压蒸汽养护制成的板材,俗称水泥压力板。 ASTM C1186-22纤…...

NoSQL概述
NoSQL概述 目录 一、为什么用NoSQL 二、什么是NoSQL 三、经典应用分析 四、N o S Q L 数 据 模 型 简 介 五、NoSQL四大分类 六、CAP BASE 一、为什么用NoSQL 1、单机MySQL的美好年代 在90年代,一个网站的访问量一般不大,用单个数据库完全可以轻松应…...
爬虫实战一、Scrapy开发环境(Win10+Anaconda3)搭建
#前言 在这儿推荐使用Anaconda进行安装,并不推荐大家用pythonpip安装,因为pythonpip的坑实在是太多了。 #一、环境中准备: Win10(企业版)Anaconda3-5.0.1-Windows-x86_64,下载地址,如果打不开…...
llama.cpp运行qwen0.5B
编译llama.cp 参考 下载模型 05b模型下载 转化模型 创建虚拟环境 conda create --prefixD:\miniconda3\envs\llamacpp python3.10 conda activate D:\miniconda3\envs\llamacpp安装所需要的包 cd G:\Cpp\llama.cpp-master pip install -r requirements.txt python conver…...
 |GET和POST两种基本请求方法有什么区别)
【接口】HTTP(3) |GET和POST两种基本请求方法有什么区别
在我面试时,在我招人面试别人时,10次能遇到7次这个问题,我听过我也说回答过: Get: 一般对于从服务器取数据的请求可以设置为get方式 Get方式在传递参数的时候,一般都会把参数直接拼接在url上 Get请求方法…...

金陵科技学院软件工程学院软件工程专业
感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦~~ 感兴趣的小伙伴可以私信我哦~~ 是笔者写的各种高质量作业和实验哦…...

Android 关于apk反编译d2j-dex2jar classes.dex失败的几种方法
目录 确认路径正确直接定位到指定目录确定目录正确,按如下路径修改下面是未找到相关文件正确操作 确认路径正确 ,即d2j-dex2jar和classes.dex是否都在一个文件夹里(大部分的情况都是路径不正确) 直接定位到指定目录 路径正确的…...

Django--admin 后台管理站点
Django最大的优点之一,就是体贴的提供了一个基于项目model创建的一个后台管理站点admin。这个界面只给站点管理员使用,并不对大众开放。虽然admin的界面可能不是那么美观,功能不是那么强大,内容不一定符合你的要求,但是…...

JavaScript(六)---【回调、异步、promise、Async】
零.前言 JavaScript(一)---【js的两种导入方式、全局作用域、函数作用域、块作用域】-CSDN博客 JavaScript(二)---【js数组、js对象、this指针】-CSDN博客 JavaScript(三)---【this指针,函数定义、Call、Apply、函数绑定、闭包】-CSDN博客 JavaScript(四)---【执…...
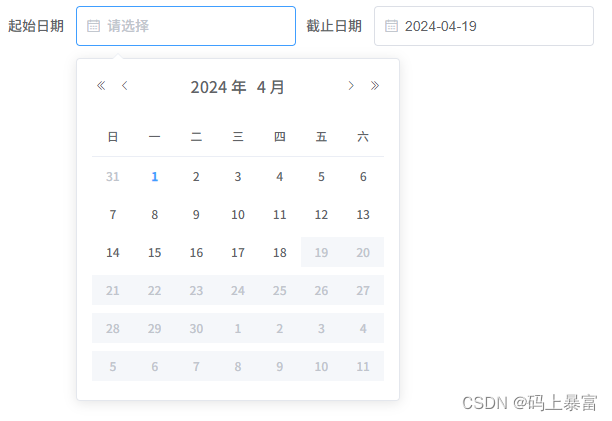
vue2+elementUi的两个el-date-picker日期组件进行联动
vue2elementUi的两个el-date-picker日期组件进行联动 <template><el-form><el-form-item label"起始日期"><el-date-picker v-model"form.startTime" change"startTimeChange" :picker-options"startTimePickerOption…...

GIN实例讲解
第一个gin程序 package mainimport ("github.com/gin-gonic/gin" )func main() {// 创建一个 Gin 引擎实例r : gin.Default()// 定义一个 GET 请求的路由,当访问 /hello 路径时执行匿名函数r.GET("/hello", func(c *gin.Context) {// 获取查询…...

开源充电桩设备监控系统技术解决方案
开源 | 慧哥充电桩平台V2.5.2(支持 汽车 电动自行车 云快充1.5、云快充1.6 微服务 ) SpringBoot设备监控系统解决方案 一、引言 1.项目背景 随着物联网技术的快速发展,设备的智能化和网络化程度日益提高。在现代工业和信息化的背景下&#x…...
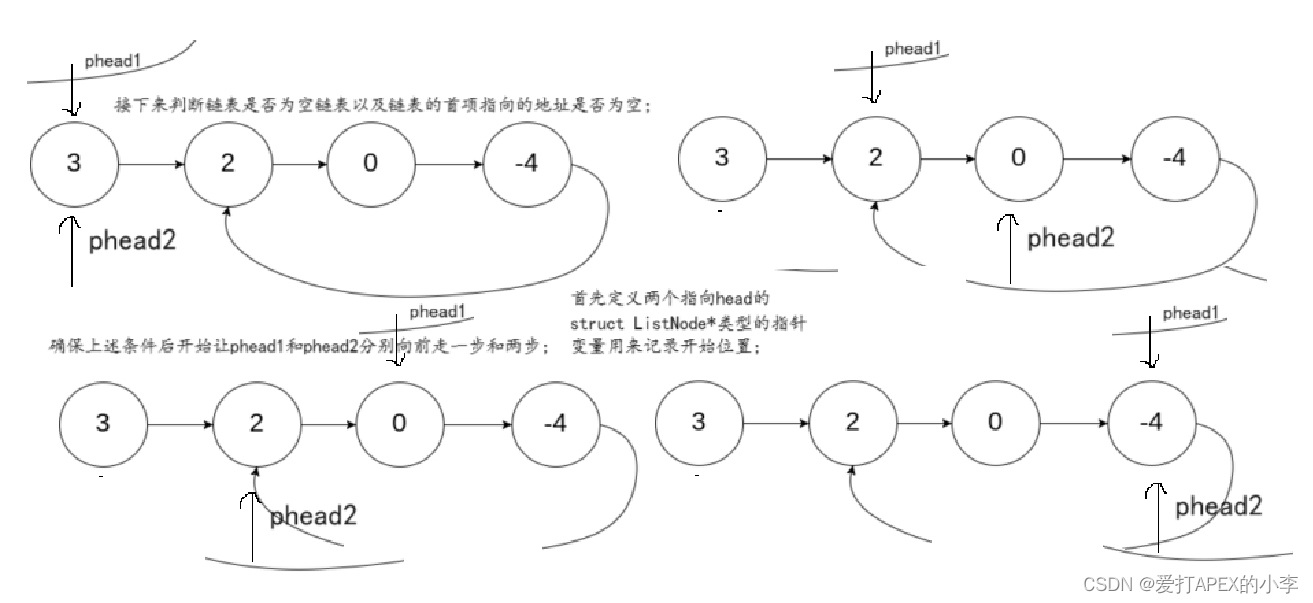
环形链表--极致的简便
一、要求 给你一个链表的头节点 head ,判断链表中是否有环。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置&a…...

WPF中TextWrapping
在 WPF(Windows Presentation Foundation)中,TextWrapping 是一个与文本布局相关的属性,用于控制文本在遇到容器边界时是否自动换行。这个属性常用于文本展示控件,如 TextBlock、TextBox、Label 等,以确保文…...
Win10 下 git error unable to create file Invalid argument 踩坑实录
原始解决方案参看:https://stackoverflow.com/questions/26097568/git-pull-error-unable-to-create-file-invalid-argument 本问题解决于 2024-02-18,使用 git 版本 2.28.0.windows.1 解决方案 看 Git 抛出的出错的具体信息,比如如下都来自…...
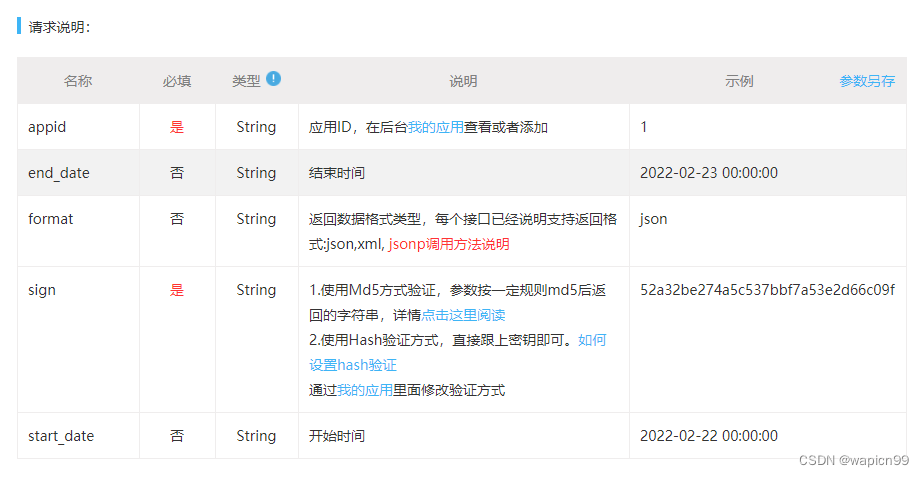
简化备案域名查询的最新API接口
随着互联网的发展,越来越多的网站和域名被注册和备案。备案域名查询是一个非常重要的功能,可以帮助用户在特定时间段内查询已备案的域名信息。现在,我将介绍一个简化备案域名查询的最新API接口,该接口可以帮助用户快速查询备案域名…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
