深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录
偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学得的结果很可能不同,即便这些训练集是来自同一个分布,对测试样本xxx,令yDy_DyD为在数据集中的标记,yyy为xxx的真实标记f(x;D)f(x;D)f(x;D)为训练集DDD上学得模型fff在上的预测输出。以回归任务为例,学习算法的期望预测为:
f(x)=ED[f(x;D)]f(x)=E_D[f(x;D)]f(x)=ED[f(x;D)]
使用样本数相同的不同训练集产生的方差为:
Var(x)=ED[f(x;D)−f(x)]\text{Var}(x)=E_D[f(x;D)-f(x)]Var(x)=ED[f(x;D)−f(x)]
噪声为:
ϵ2=ED[(yD−y)2]\epsilon^2=E_D[(y_D-y)^2]ϵ2=ED[(yD−y)2]
期望输出与真实标记的差别称为偏差(Bias),即:
bias2(x)=(f(x)−y)2\text{bias}^2(x)=(f(x) - y)^2bias2(x)=(f(x)−y)2
为便于讨论,假定噪声期望为零,即ED[(yD−y)]=0E_D[(y_D-y)]=0ED[(yD−y)]=0。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
ED[(f(x;D)−yD)2]=ED[(f(x;D)−fˉ(x)+fˉ(x)−yD)2]=ED[(f(x;D)−fˉ(x)]+(fˉ(x)−y)2+ED[(yD−y)2]=bias2(x)+Var(x)+ϵ2\begin{align*} E_D[(f(x; D) - y_D)^2] &= E_D[(f(x; D) - \bar{f}(x) + \bar{f}(x) - y_D)^2]\\ &= E_D[(f(x; D) - \bar{f}(x)] + (\bar{f}(x) - y)^2 + E_D[(y_D - y)^2]\\ &= \text{bias}^2(x) + \text{Var}(x) + \epsilon^2 \end{align*} ED[(f(x;D)−yD)2]=ED[(f(x;D)−fˉ(x)+fˉ(x)−yD)2]=ED[(f(x;D)−fˉ(x)]+(fˉ(x)−y)2+ED[(yD−y)2]=bias2(x)+Var(x)+ϵ2
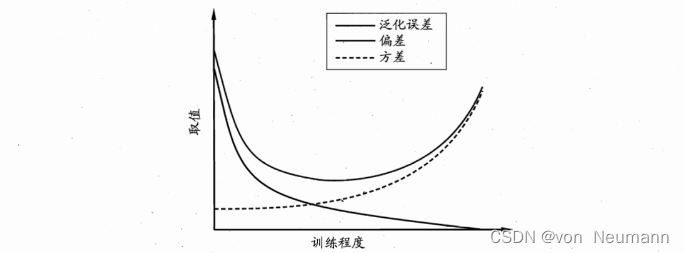
也就是说,泛化误差可分解为偏差、方差与噪声之和。回顾偏差、方差、噪声的含义:偏差度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力;方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响;噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。偏差方差分解说明,泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小一般来说,偏差与方差是有冲突的,这称为偏差方差窘境(Bias-Variance Dilemma)。下图给出了一个示意图。给定学习任务,假定我们能控制学习算法的训练程度,则在训练不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,此时偏差主导了泛化错误率;随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据发生的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率:在训练程度充足后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生过拟合,
参考文献:
[1] 周志华. 机器学习[M]. 清华大学出版社, 2016.
相关文章:

深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...
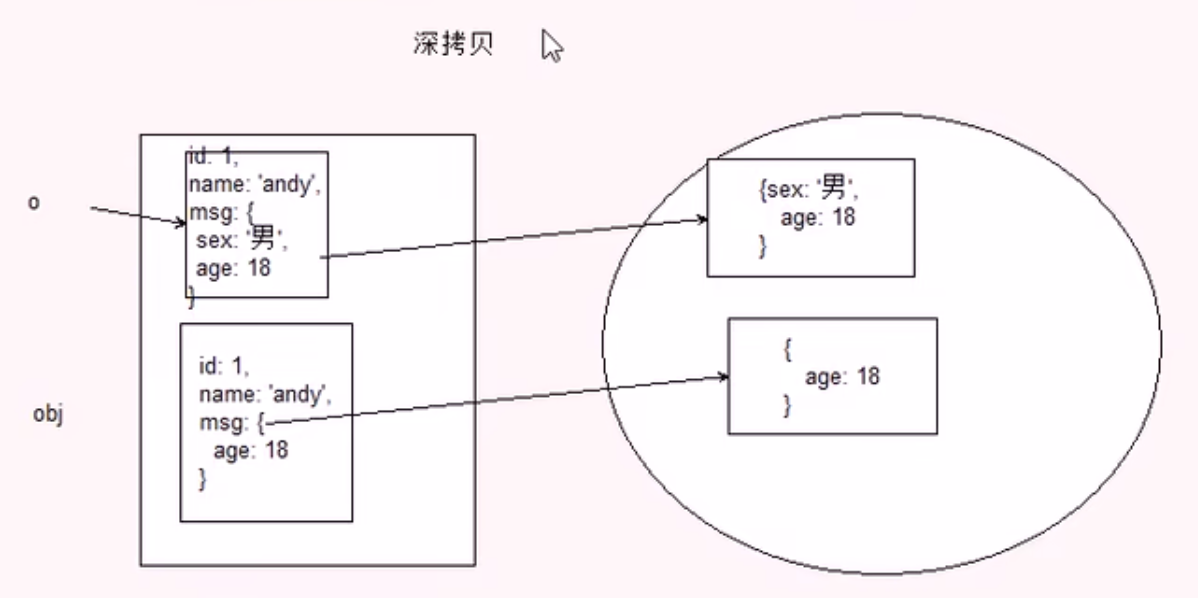
JavaScript 高级3 :函数进阶
JavaScript 高级3 :函数进阶 Date: January 19, 2023 Text: 函数的定义和调用、this、严格模式、高阶函数、闭包、递归 目标: 能够说出函数的多种定义和调用方式 能够说出和改变函数内部 this 的指向 能够说出严格模式的特点 能够把函数作为参数和返…...
【项目】Java树形结构集合分页,java对list集合进行分页
Java树形结构集合分页需求难点实现第一步:查出所有树形集合数据 (需进行缓存处理)selectTree 方法步骤:TreeUtil类:第二步:分页 GoodsCategoryController分页getGoodsCategoryTree方法步骤:第三…...
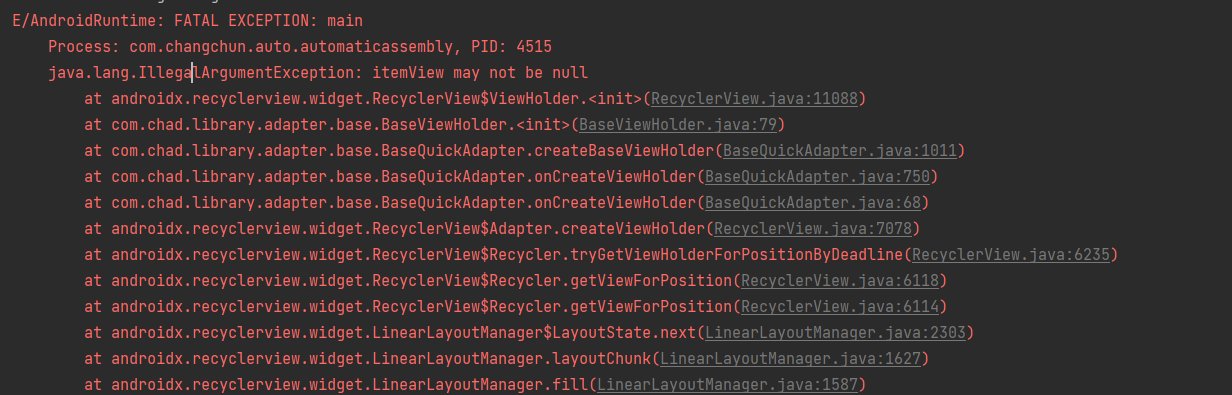
java.lang.IllegalArgumentException: itemView may not be null
报错截图:场景介绍:在使用recycleView 自动递增数据,且自动滚动到最新行; 当数据达到273条 时出现ANR;项目中 全部的列表适配器使用的三方库:BaseRecyclerViewAdapterHelper (很早之前的项目&am…...
[ 攻防演练演示篇 ] 利用 shiro 反序列化漏洞获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

达人合作加持品牌布局,3.8女神玩转流量策略!
随着迅猛发展的“她经济”,使社区本就作为内容种草的平台,自带“营销基因”。在3.8女神节即将到来之际,如何充分利用平台女性资源优势,借助达人合作等手段,实现迅速引流,来为大家详细解读下。一、小红书节日…...
观点丨Fortinet谈ChatGPT火爆引发的网络安全行业剧变
FortiGuard报告安全趋势明确指出“网络攻击者已经开始尝试AI手段”,ChatGPT的火爆之际的猜测、探索和事实正在成为这一论断的佐证。攻守之道在AI元素的加持下也在悄然发生剧变。Fortinet认为在攻击者利用ChatGPT等AI手段进行攻击的无数可能性的本质,其实…...

工业企业用电损耗和降损措施研究
来自用电设备和供配电系统的电能损耗。而供配电系统的电能损耗,包括企业变配电设备、控制设备企业在不断降低生产成本,追求经济效益的情况下,进一步降低供配电系统中的电能损耗,使电气设摘要:电网电能损耗是一个涉及面很广的综合性问题,主要包括管理损耗和技术损耗两部分…...

高并发、高性能、高可用
文章目录一、高并发是什么?二、 高性能是什么三、 高可用什么是一、高并发是什么? 示例:高并发是现在互联网分布式框架设计必须要考虑的因素之一,它是可以保证系统能被同时并行处理很多请求,对于高并发来说࿰…...
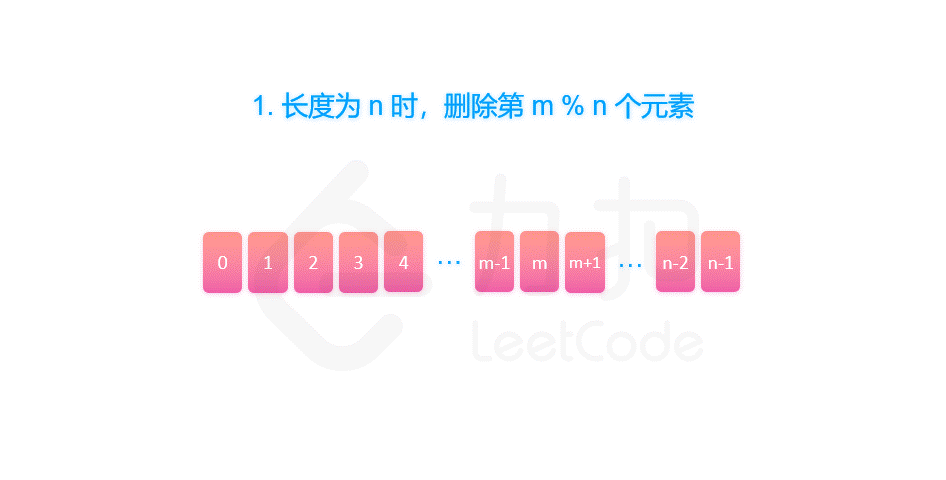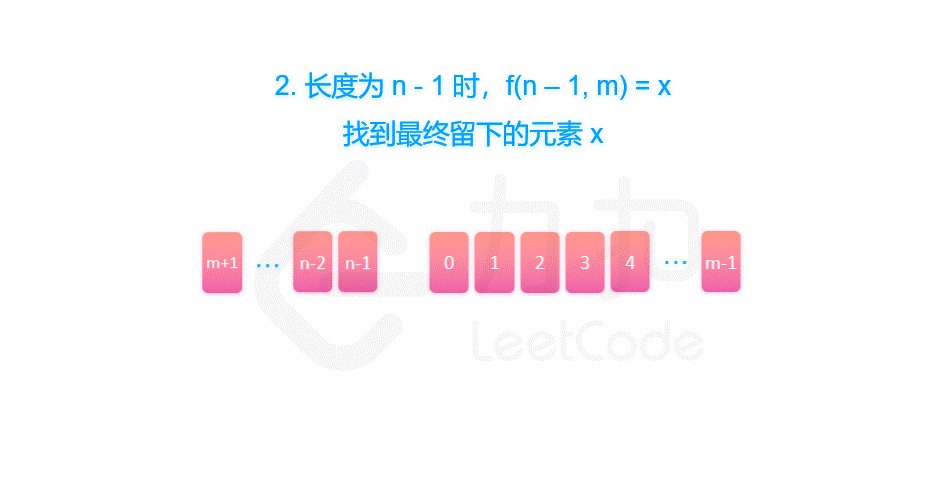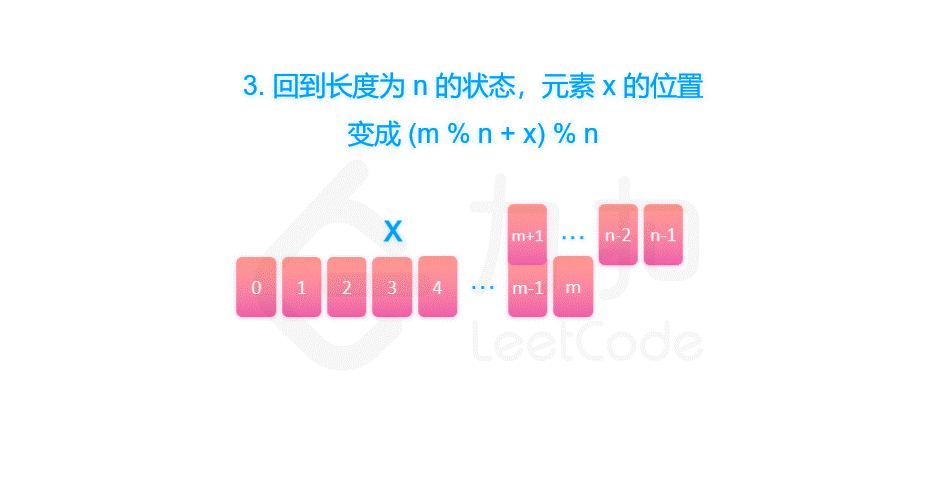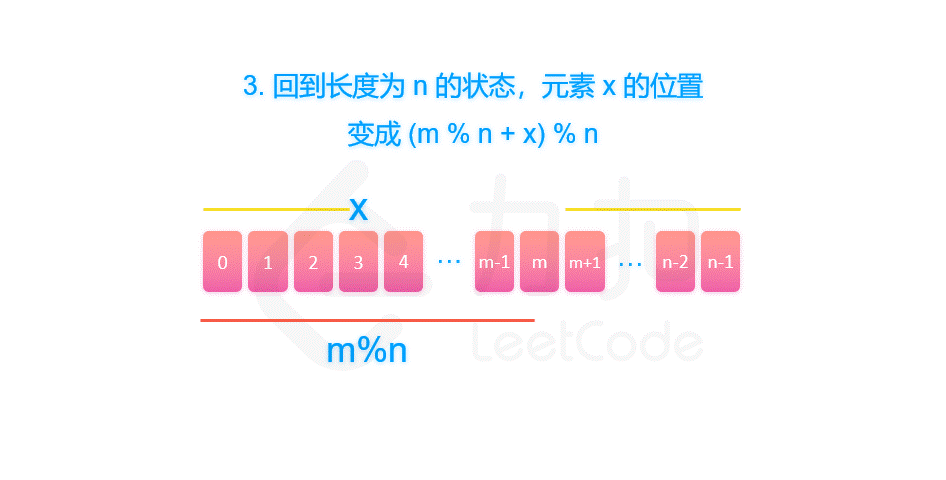
剑指 Offer 62. 圆圈中最后剩下的数字
摘要 剑指 Offer 62. 圆圈中最后剩下的数字 一、约瑟夫环解析 题目中的要求可以表述为:给定一个长度为 n 的序列,每次向后数 m 个元素并删除,那么最终留下的是第几个元素?这个问题很难快速给出答案。但是同时也要看到ÿ…...
概率论小课堂:高斯分布(正确认识大概率事件)
文章目录 引言I 预备知识1.1 正态分布1.2 置信度1.3 风险II 均值、标准差和发生概率三者的关系。2.1 “三∑原则”2.2 二班成绩比一班好的可能性2.3 减小标准差引言 泊松分布描述的是概率非常小的情况下的统计规律性。学习高斯分布来正确认识大概率事件,随机变量均值的差异和偶…...

剑指 Offer 43. 1~n 整数中 1 出现的次数
摘要 剑指 Offer 43. 1~n 整数中 1 出现的次数 一、数学思维解析 将1~ n的个位、十位、百位、...的1出现次数相加,即为1出现的总次数。 设数字n是个x位数,记n的第i位为ni,则可将n写为 nxnx−1⋯n2n1: 称" …...

如何成为程序员中的牛人/高手?
目录 一、牛人是怎么成为牛人的? 二、关于牛人的一点看法 三、让程序员与业务接壤,在开发团队中“升级” 四、使用低代码平台 目标效果 五、最后 祝伟大的程序员们梦想成真、码到成功! 一、牛人是怎么成为牛人的? 最近在某…...
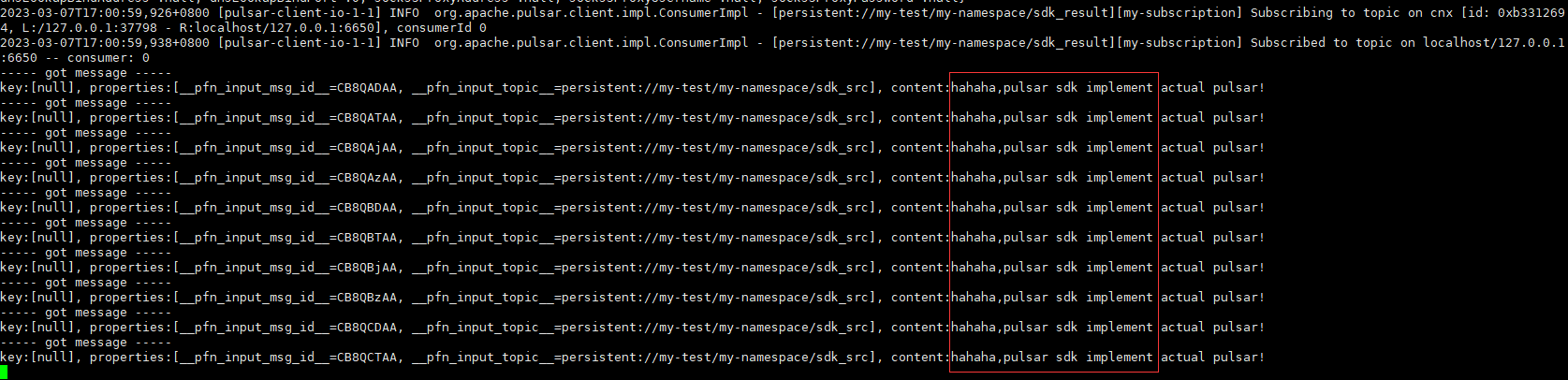
云原生时代顶流消息中间件Apache Pulsar部署实操之轻量级计算框架
文章目录Pulsar Functions(轻量级计算框架)基础定义工作流程函数运行时处理保证和订阅类型窗口函数定义窗口类型滚动窗口滑动窗口函数配置函数示例有状态函数示例窗口函数示例自定义函数开发定义原生语言接口示例Pulsar函数SDK示例Pulsar Functions(轻量级计算框架) 基础定义 …...
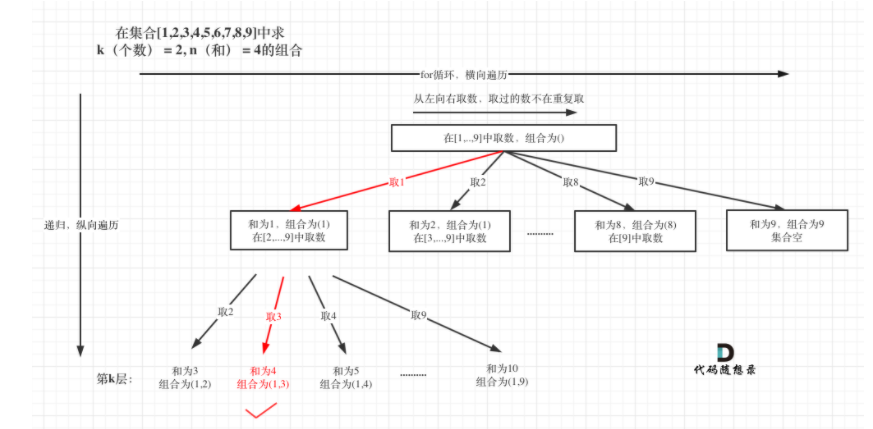
数据结构刷题(十九):77组合、216组合总和III
1.组合题目链接过程图:先从集合中取一个数,再依次从剩余数中取k-1个数。思路:回溯算法。使用回溯三部曲进行解题:递归函数的返回值以及参数:n,k,startIndex(记录每次循环集合从哪里开始遍历的位…...
PyQt 做美*女GIF设置桌面,每天都很爱~
人生苦短,我用python 要说程序员工作的最大压力不是来自于工作本身, 而是来自于需要不断学习才能更好地完成工作, 因为程序员工作中面对的编程语言是在不断更新的, 同时还要学习熟悉其他语言来提升竞争力… 好了,学习…...

[渗透测试笔记] 54.日薪2k的蓝队hw中级定级必备笔记系列篇3之域渗透黄金票据和白银票据
前文链接 [渗透测试笔记] 52.告别初级,日薪2k的蓝队hw中级定级必备笔记 [渗透测试笔记] 53.日薪2k的蓝队hw中级定级必备笔记2 文章目录 Kerberos认证协议NTLM认证协议Kerberos和NTLM比较黄金票据原理黄金票据条件复现过程白银票据原理白银票据条件复现过程黄金票据和白银票据…...

【异常】Spring Cloud Gateway网关自定义过滤器无法获取到请求体body的内容?不存在的!
一、需求说明 项目要使用到网关SpringCloud Gateway进行验签,现在定义了一个过滤器ValidateSignFilter, 我希望,所以过网关SpringCloud Gateway的请求,都能够校验一下请求头,看看是否有Sign这个字段放在请求头中。 二、异常说明 但是,我遇到了SpringCloud Gateway网关…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

PostgreSQL 与 SQL 基础:为 Fast API 打下数据基础
在构建任何动态、数据驱动的Web API时,一个稳定高效的数据存储方案是不可或缺的。对于使用Python FastAPI的开发者来说,深入理解关系型数据库的工作原理、掌握SQL这门与数据库“对话”的语言,以及学会如何在Python中操作数据库,是…...

uniapp获取当前位置和经纬度信息
1.1. 获取当前位置和经纬度信息(需要配置高的SDK) 调用uni-app官方API中的uni.chooseLocation(),即打开地图选择位置。 <button click"getAddress">获取定位</button> const getAddress () > {uni.chooseLocatio…...
