【信号与系统笔记】第一章 绪论
1.1信号传输系统
信息传输的任务
将带有信息的信号,通过某种系统由发送者传送给接收者。
通信系统的组成
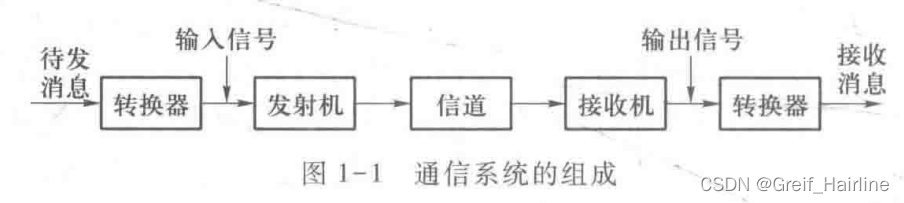
- 转换器:把消息转换为电信号或者把电信号还原成消息
- 信道:信号传输的通道,广义上来说。发射机和接收机也可以是信道的一部分
- 发射机 :把电信号转换成适合传输的大功率射频信号
- 接收机: 把发射机发射的信号转换成电信号
1.2信号的概念
定义
随着时间变化的物理量。更广义的说,万物皆可为信号。
描述
- 时域法
- 频域法(变换域)
分类
确定与随机信号
- 确定信号:可用确定的时间函数表示
- 随机信号:不可用确定的时间函数表示,只能用统计特性描述
- 联系: 确定信号是一种近似的、理想化的随机信号
连续与离散信号
- 连续信号:时间变量是连续的
- 离散信号:时间变量取离散值
- 数字信号:时间和幅度上都是离散的
- 模拟信号:时间和幅度上都是连续的
周期与非周期信号
- 绝对的周期信号不存在,工程上的周期信号指在较长时间内满足周期性
- 两个周期信号相加/相乘不一定是周期信号
- 连续周期信号抽样后不一定是周期信号(抽样后的离散信号的周期等于整数才可以)
- 因果周期信号不是周期信号如sintε(t),但是是功率信号
能量与功率信号
定义
- 能量信号:信号能量为非零有限值,功率为0
- 功率信号:信号平均功率为非零有限值,能量为无穷
- 非功非能信号:能量和功率都为无限值即为非功非能信号(典型信号:tε(t))
计算
1.能量计算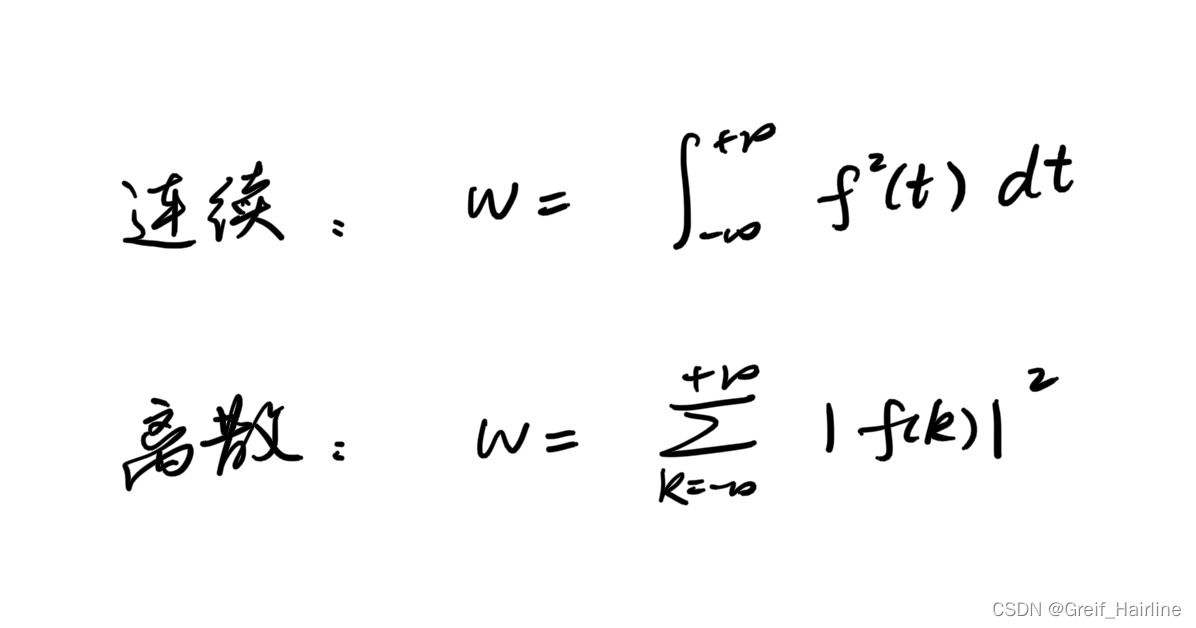
2.功率计算
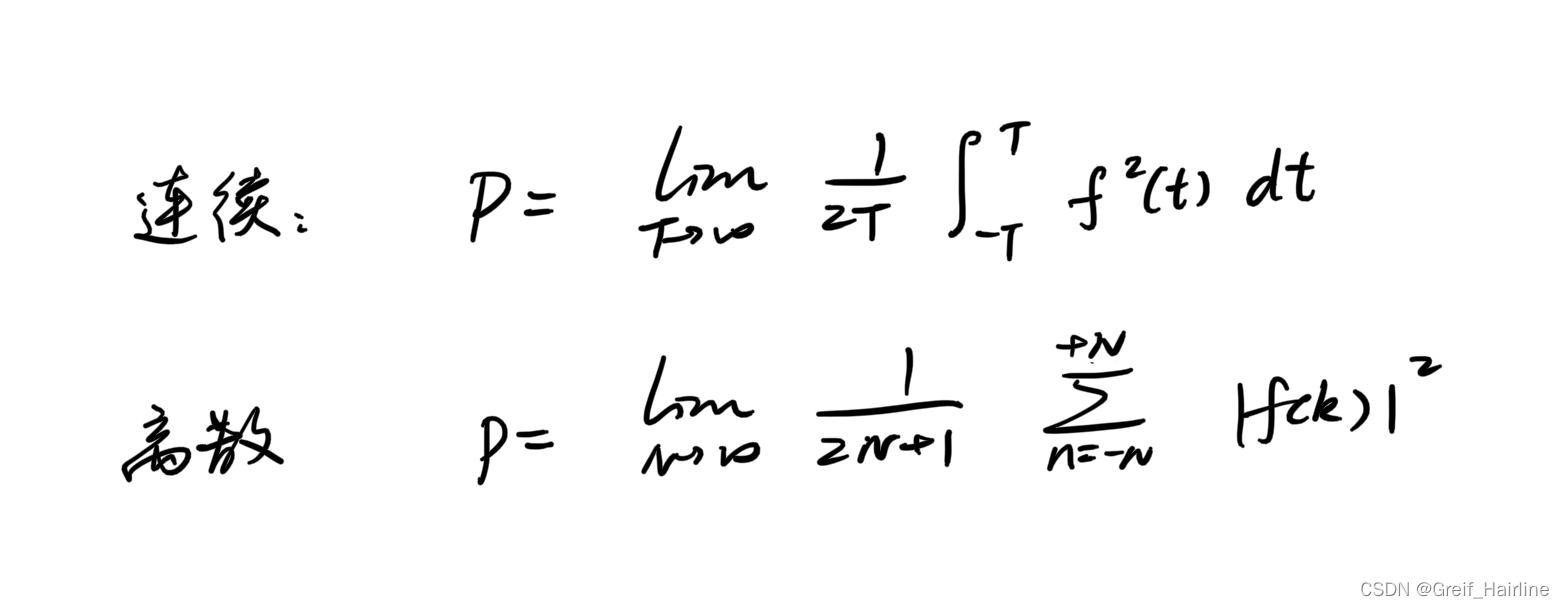
注意点
- 周期信号/周期信号的线性叠加一定是功率信号,非周期信号也有可能是功率信号
- 能量信号一定是非周期信号
- 有限时间信号一定是能量信号
- 因果周期信号也是功率信号如sintε(t)
- 以下说法是错误的
两个功率信号之和/积为功率信号(存在抵消的情况)
能量信号与功率信号乘积必为能量信号
随机信号必然是非周期信号
1.3信号的简单处理
注意:所有的变换针对自变量而言
- 叠加
- 相乘
- 平移(延时)
- 反褶
- 尺度变换
1.4系统的概念
定义
由若干互有关联的单元组成的、具有某种功能、用来达到某些特定目标的有机整体
描述方法
- 输入输出方程
- 框图模型
- 系统函数
- 状态方程
分类
线性和非线性系统
线性系统
定义:同时符合线性性和叠加性的系统
注意点:积分和微分都是线性运算
非线性系统
定义:不符合线性性和叠加性的系统
判定方法
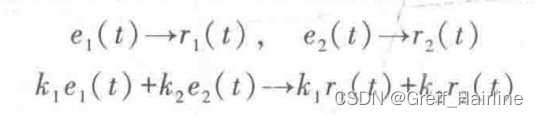
描述方法
线性系统可用线性微分方程或差分方程描述;非线性系统可用非线性微分方程或差分方程描述
非时变和时变系统
定义
非时变系统:系统性质不随时间变化,系统由定常参数元件构成
时变系统:系统性质随时间发生变化
判定方法
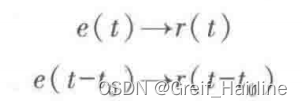
描述方法
非时变系统可用常系数线性微分方程来描述
连续时间和离散时间系统
连续时间系统:处理连续时间信号的系统
离散时间系统:处理离散时间信号的系统
因果和非因果系统
因果系统:符合因果规律的系统,即系统响应不可能出现在施加激励之前
非因果系统:不符合因果规律的系统
稳定和非稳定系统
稳定系统:在有限激励下产生有限响应的系统
非稳定系统:不满足上述条件的系统
1.5线性非时变系统的分析
系统的研究内容
分析:已知系统特性和激励信号,求系统输出
识别:已知输入和输出信号,求系统特性
设计:已知输入和目标输出信号,构造系统
系统分析的步骤
1.建立数学模型
2.进行分析
3.物理解释
系统分析方法
LTI连续时间系统
时域法
经典法:微分方程(直接法)
算子法:近代时域法和卷积法
变换域法
频域法:傅里叶变换
复频域法:拉普拉斯变换
状态方程法
LTI离散时间系统
时域法
经典法
算子法
变换域法:Z变换
状态方程法
相关文章:
【信号与系统笔记】第一章 绪论
1.1信号传输系统 信息传输的任务 将带有信息的信号,通过某种系统由发送者传送给接收者。 通信系统的组成 转换器:把消息转换为电信号或者把电信号还原成消息信道:信号传输的通道,广义上来说。发射机和接收机也可以是信道的一部分…...
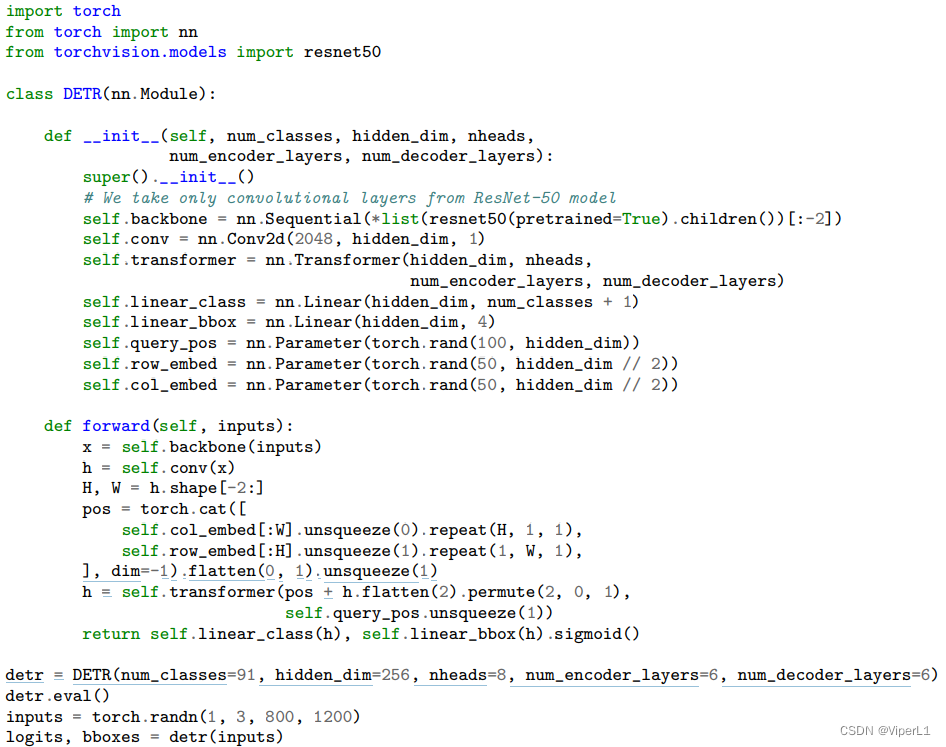
[神经网络]DETR目标检测网络
一、概述 相较于传统目标检测,DETR是一种纯端到端的网络。它不再需要NMS(非极大值抑制,用于去除多余的预测框)和生成anchor。 DETR提出了一个新的目标函数(二分图匹配),这个函数可以强制网络输出一个独一无二的预测值&…...

【服务器管理】connection refused问题解决
简述 在配置服务器的时候,遇到了这个问题。我当时明明已经搭建好了服务,但是我在客户端比如手机上,却怎么都连不上服务器。看日志的话显示的是connection refuesed timeout 这种情况,大概率是服务器的端口没有被打开。 我们只需…...

2023_华为OD机试真题_Python_047_整理扑克牌
整理扑克牌 题目描述 给定一组数字,表示扑克牌的牌面数字,忽略扑克牌的花色,请按如下规则对这一组扑克牌进行整理: 步骤1. 对扑克牌进行分组,形成组合牌,规则如下: 当牌面数字相同张数大于等于4时,组合牌为“炸弹”;3张相同牌面数字 + 2张相同牌面数字,且3张牌与2…...
吐血整理,自动化测试pytest测试框架,资深测试带你少走弯路......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 Pytest框架详解 py…...

SAP BASE64加密及解密
简介:BASE64是一种编码方法,它是一种基于用64个可打印字符来表示二进制数据的表示方法,主要应用于数据存储,传输,打印它是用64个可打印字符表示二进制所有数据方法。由于2的6次方等于64,所以可以用每6个位元…...
【页面无响应】Web页面经常无响应前端如何定位与优化(已解決)
【写在前面】客户现场应用我们的系统时候,发现用着用着就出现1个页面无响应现象,给客户带来极其不好的体验,尤其是当重要工作汇报演示时,就给我看无响应,浏览器崩溃?这样对产品的发展无疑是致命的伤&#x…...

隐私计算 FATE - 多分类神经网络算法测试
一、说明 本文分享基于 Fate 使用 横向联邦 神经网络算法 对 多分类 的数据进行 模型训练,并使用该模型对数据进行 多分类预测。 二分类算法:是指待预测的 label 标签的取值只有两种;直白来讲就是每个实例的可能类别只有两种 (0 或者 1)…...
)
Codeforces Round 853 (Div. 2)
Codeforces Round 853 (Div. 2) C. Serval and Toxels Arrays 思路: 求任意两个组合的元素个数。 注意到,其实每个元素都是独立的。他在任意组合的出现情况组成的贡献是可以分开讨论的。我们讨论元素x。假设x在m1个数组中出现了cnt次(一个…...
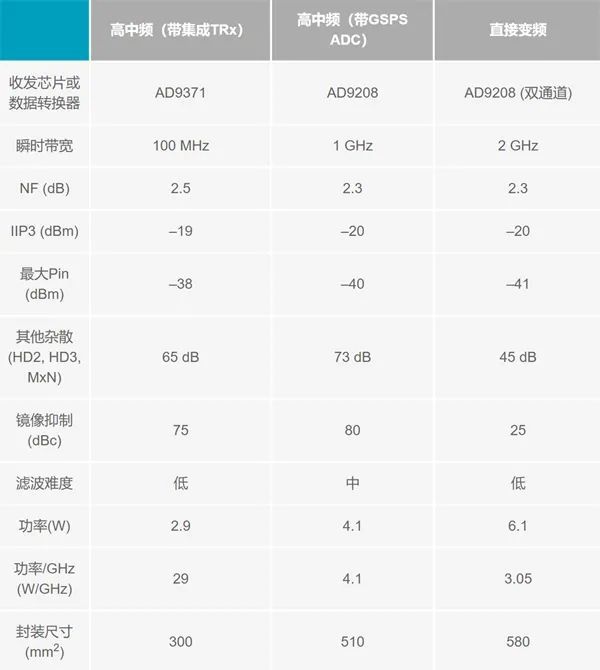
Ka频段需要更多带宽?
随着全球连接需求的增长,许多卫星通信(satcom)系统日益采用Ka频段,对数据速率的要求也水涨船高。目前,高性能信号链已经能支持数千兆瞬时带宽,一个系统中可能有成百上千个收发器,超高吞吐量数据速率已经成为现实。 另…...

初学pyinstaller打包过程中的一些问题
记录一下使用pyinstaller打包过程中的一些问题: 不安装虚拟环境打包,直接打包,一般不会出现什么问题,但是打包的exe很大,把所有模块和依赖库也一起打包了。 建议使用虚拟环境打包,安装必要的包࿰…...

第七章:Java常用类
第七章:Java常用类 7.1:字符串相关的类 String的特性 String表示是字符串,使用一对""引起来表示。 String声明为final的,不可被继承。 String实现了Serializable、Comparable接口,表示字符是支持序列化和…...

Apk加固后多渠道打包
之前一直使用360加固宝进行apk的加固打包,可以一键加固并打多渠道打包。但是,现在360加固宝收费了,在进行加固,多渠道打包,就得一步一步自己操作了,会很繁琐。所以,本文使用 360加固美团Wallet …...

K8S + ISTIO 金丝雀部署的例子
金丝雀发布(Canary):也是一种发布策略,和国内常说的灰度发布是同一类策略。蓝绿部署是准备两套系统,在两套系统之间进行切换,金丝雀策略是只有一套系统,逐渐替换这套系统。 Istio 提供一种简单的…...

python自带数据的模型合集
鸢尾花----聚类 Python鸢尾花数据集通常用于分类问题, 这些模型都可以通过Python中的Scikit-learn库进行实现。同时,也可以对这些模型进行参数调优以提高模型的准确性。 Logistic Regression(逻辑回归): 逻辑回归是一…...

女生学习大数据怎么样~有前景么
当前大数据发展前景非常不错,且大数据领域对于人才类型的需求比较多元化,女生学习大数据也会有比较多的工作机会。大数据是一个交叉学科涉及到的知识量比较大学习有一定的难度,女生则有女生的优势,只要认真学习了都是可以做大数据…...
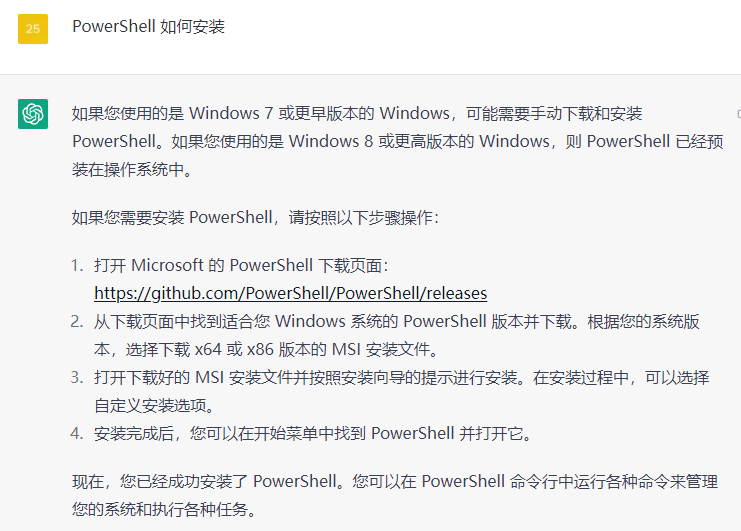
统计代码量
一 windows 在 Windows 系统上,您可以使用 PowerShell 命令行工具来统计项目的代码量。下面是使用 PowerShell 统计项目代码量的步骤: 打开 PowerShell 终端:按下 Win X 键,选择「Windows PowerShell(管理员…...

uniapp在线升级关联云空间
升级中心 uni-upgrade-center - App: https://ext.dcloud.net.cn/plugin?id4542 App升级中心 uni-upgrade-center文档: https://uniapp.dcloud.net.cn/uniCloud/upgrade-center.html#uni-upgrade-center-app 升级中心 uni-upgrade-center - Admin&#…...
学习streamlit-2
首先视频快速预览下今天的学习内容: Streamlit Shorts: How to make a button今天继续学习streamlit,首先激活之前建立的虚拟环境: ❯ conda activate streamlit-env (streamlit-env) ~ via 🐍 v3.9.16 via …...

Vscode中Vue文件保存格式化、 ElementUI、Font Awesome俩大插件使用
Vscode中Vue文件老一片红色出现格式错误??如何运行别人的项目(没有node_modules文件)??选用组件与图标?? 解决问题一 前提有:Prettier ESLint插件、ESLint插件 1.打开s…...

Springboot+vue房屋租赁管理系统的设计与实现
文章目录前言源码获取详细视频演示具体实现截图后端框架SpringBoot前端框架Vue持久层框架MyBaits成功系统案例:数据库前言 博主介绍:CSDN特邀作者、985高校计算机专业毕业、现任某互联网大厂高级全栈开发工程师、Gitee/掘金/华为云/阿里云/GitHub等平台持续输出高质…...

终极指南:如何让Maccy实现跨屏幕剪贴板管理,提升多显示器工作效率
终极指南:如何让Maccy实现跨屏幕剪贴板管理,提升多显示器工作效率 【免费下载链接】Maccy Lightweight clipboard manager for macOS 项目地址: https://gitcode.com/gh_mirrors/ma/Maccy Maccy作为一款轻量级macOS剪贴板管理器(Light…...
—— 视图容器 之 View 视图组件)
uni-app x 学习系列(五)—— 视图容器 之 View 视图组件
<view> 是 UNI-APP 中布局的基本元素,类似于 HTML 中的 <div> 标签,主要用于创建块级容器。 示例:index.uvue <template><view class"container"><view class"header"><text>轮播图…...

为什么选择matrixmultiplication.xyz?5大优势让线性代数学习事半功倍
为什么选择matrixmultiplication.xyz?5大优势让线性代数学习事半功倍 【免费下载链接】matrixmultiplication.xyz 项目地址: https://gitcode.com/gh_mirrors/ma/matrixmultiplication.xyz matrixmultiplication.xyz是一款专为教育设计的交互式矩阵乘法计算…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
