代码学习记录40---动态规划
随想录日记part40
t i m e : time: time: 2024.04.10
主要内容:今天开始要学习动态规划的相关知识了,今天的内容主要涉及:
买卖股票的最佳时机加强版。
- 123.买卖股票的最佳时机III
- 188.买卖股票的最佳时机IV
动态规划五部曲:
【1】.确定dp数组以及下标的含义
【2】.确定递推公式
【3】.dp数组如何初始化
【4】.确定遍历顺序
【5】.举例推导dp数组
Topic1买卖股票的最佳时机|||

思路:
接下来进行动规五步曲:
1.确定dp数组以及下标的含义:
一天一共就有五个状态,
- 0.没有操作 (其实我们也可以不设置这个状态)
- 1.第一次持有股票
- 2.第一次不持有股票
- 3.第二次持有股票
- 4.第二次不持有股票
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
需要注意:dp[i][1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。例如 dp[i][1] ,并不是说 第i天一定买入股票,有可能 第 i-1天 就买入了,那么 dp[i][1] 延续买入股票的这个状态。
2.确定递推公式:
【达到dp[i][1]有两个操作】:
操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i]
操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
那么dp[i][1]究竟选 dp[i-1][0] - prices[i],还是dp[i - 1][1]呢?
一定是选最大的,所以 dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
【dp[i][2]也有两个操作】:
操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
同理可推出剩下状态部分:
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);3.dp数组如何初始化
dp数组如何初始化
第0天没有操作,这个最容易想到,就是0,即:dp[0][0] = 0;
第0天做第一次买入的操作,dp[0][1] = -prices[0];
第0天做第一次卖出的操作,这个初始值应该是多少呢?
此时还没有买入,怎么就卖出呢? 其实大家可以理解当天买入,当天卖出,所以dp[0][2] = 0;
第0天第二次买入操作,初始值应该是多少呢?应该不少同学疑惑,第一次还没买入呢,怎么初始化第二次买入呢?
第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后再买入一次(第二次买入),那么现在手头上没有现金,只要买入,现金就做相应的减少。
所以第二次买入操作,初始化为:dp[0][3] = -prices[0];
同理第二次卖出初始化dp[0][4] = 0;
4.确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
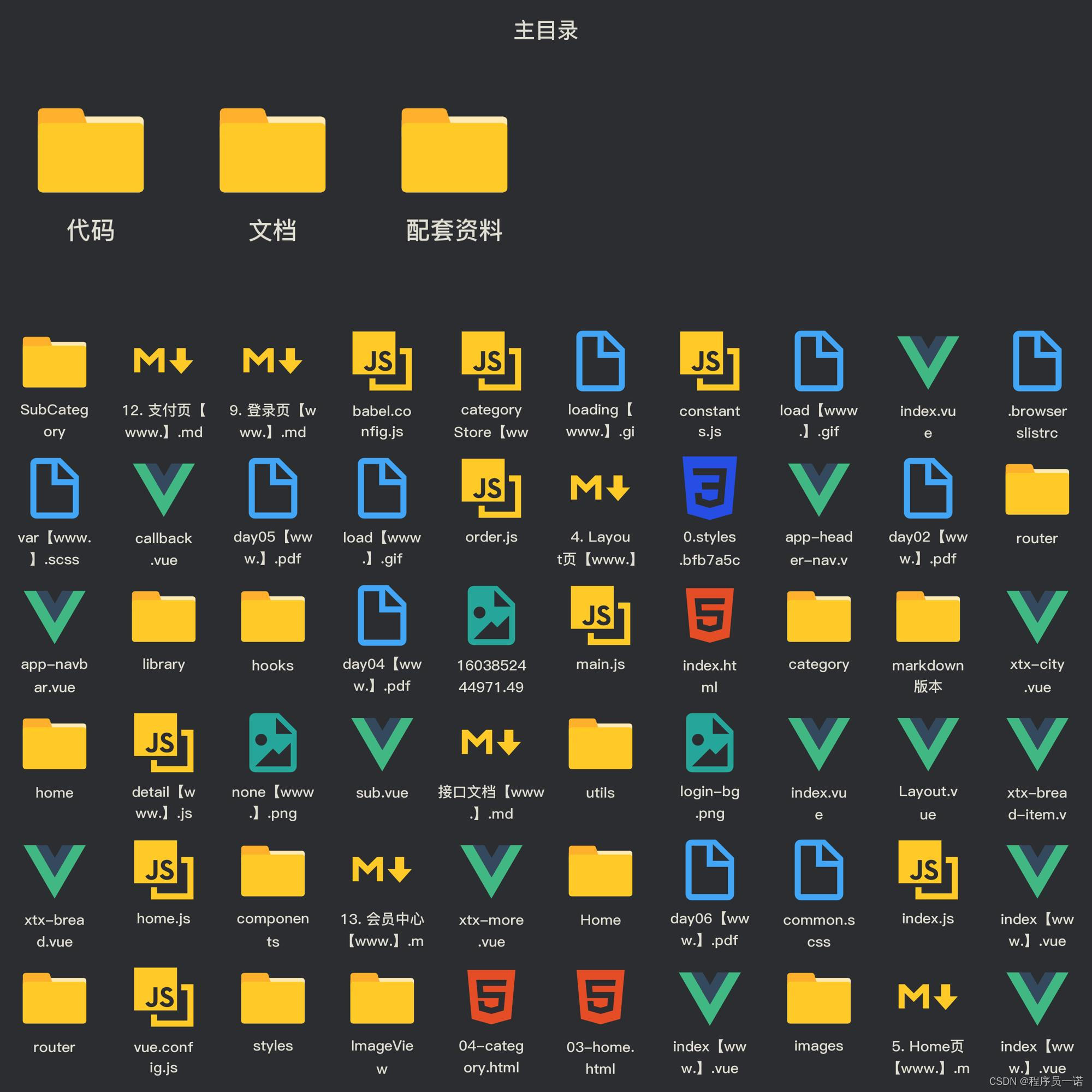
5.举例推导dp数组
以输入[1,2,3,4,5]为例
代码如下:
class Solution {class Solution {public int maxProfit(int[] prices) {// 定义dpint len = prices.length;int[][] dp = new int[len][5];// 初始化dp[0][1] = -prices[0];dp[0][3] = -prices[0];// 状态转移for (int i = 1; i < len; i++) {dp[i][0] = dp[i - 1][0];dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);dp[i][2] = Math.max(dp[i - 1][1] + prices[i], dp[i - 1][2]);dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = Math.max(dp[i - 1][3] + prices[i], dp[i - 1][4]);}return dp[len - 1][4];}
}时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( n ∗ 5 ) O(n*5) O(n∗5)
Topic2买卖股票的最佳时机IV
题目:

思路:
参考上一题
class Solution {public int maxProfit(int k, int[] prices) {// 定义dpint len = prices.length;int[][] dp = new int[len][2 * k + 1];// 初始化for (int i = 1; i < 2 * k + 1; i = i + 2) {dp[0][i] = -prices[0];}for (int i = 1; i < len; i++) {for (int j = 0; j < 2 * k - 1; j = j + 2) {dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = Math.max(dp[i - 1][j + 1] + prices[i], dp[i - 1][j + 2]);}}return dp[len - 1][2 * k];}
}
时间复杂度: O ( n ∗ k ) O(n*k) O(n∗k)
空间复杂度: O ( n ∗ k ) O(n*k) O(n∗k)
相关文章:

代码学习记录40---动态规划
随想录日记part40 t i m e : time: time: 2024.04.10 主要内容:今天开始要学习动态规划的相关知识了,今天的内容主要涉及: 买卖股票的最佳时机加强版。 123.买卖股票的最佳时机III 188.买卖股票的最佳时机…...

java八股——消息队列MQ
上一篇传送门:点我 目前只学习了RabbitMQ,后续学习了其他MQ后会继续补充。 MQ有了解过吗?说说什么是MQ? MQ是Message Queue的缩写,也就是消息队列的意思。它是一种应用程序对应用程序的通信方法,使得应用…...
【前端Vue】Vue3+Pinia小兔鲜电商项目第5篇:整体认识和路由配置,本资源由 收集整理【附代码文档】
Vue3ElementPlusPinia开发小兔鲜电商项目完整教程(附代码资料)主要内容讲述:认识Vue3,使用create-vue搭建Vue3项目1. Vue3组合式API体验,2. Vue3更多的优势,1. 认识create-vue,2. 使用create-vue创建项目,1. setup选项的写法和执行…...

前端项目部署教程——有域名无证书
一、拉取nginx镜像 docker pull nginx //先拉取nginx镜像二、打包前端项目 1、将Vue打包项目传输到/usr/local/vue/下blog和admin文件夹下 2、在/usr/local/nginx下创建nginx.conf文件,格式如下: events {worker_connections 1024; }http {include …...

后端项目部署教程
一、打包jar包 lyamanoblog-server-0.0.1.jar ps:运行时可能会提醒不能有大写字母,所以用的都是小写字母 二、编写Dockerfile文件 FROM java:8 VOLUME /tmp ADD lyamanoblog-server-0.0.1.jarblog.jar ENTRYPOINT ["java","-Djava.securit…...

【微命令】git 如何修改某个分支的名字(git branch -m newbranch)
简要信息,快速记录 命令 # 切换到某个需要修改的分支 git checkout oldbranch# 修改分支名字 git branch -m newbranch假设作为git设计者,要用来修改branch的命令,那么就是 git branch作为前缀,然后进一步修改的命令是branch相关…...

Unity UI 优化技巧
将画布分割为多个 问题:当 UI Canvas 的任何元素发生变化时,都会影响整个 Canvas。 Canvas 是 Unity UI 的重要组成部分。它创建一个网格来表示放置在其顶部的 UI 元素,在 UI 元素更改时重建网格,并调用 GPU 来渲染实际的用户界面。 创建这些网络可能非常昂贵。UI 元素应…...

前端学习之DOM编程案例:抽奖案例
代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>抽奖案例</title><style>*{margin: 0;padding: 0;}</style> </head> <body><div id"container"&g…...

解决windows下Qt Creator显示界面过大的问题
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT❤️感谢大家点赞👍收藏⭐评论✍️ 目录 问题描述 解决方法 1、右击此电脑--->属性 2、点击高级系统设置--->点击环境变量 3、 找到系…...

MySQL 通信协议 tcp c/s架构 jdbc java
简介 服务器启动后,会使用 TCP 监听一个本地端口,当客户端的连接请求到达时,就会执行三段握手以及 MySQL 的权限验证;验证成功后,客户端开始发送请求,服务器会以响应的报文格式返回数据;当客户…...
蓝桥杯第十三届电子类单片机组决赛程序设计
前言 一、决赛题目 1.比赛题目 2.题目解读 二、功能实现 1.关于定时器资源 1)超声波和NE555需要的定时器资源 2)定时器2 2.单位切换 3.数据长度不足时,高位熄灭 4.AD/DA多通道的处理 5.PWM输出 6.长按功能的实现 三、完整代码演…...

【Entity Framework】如何使用EF中的生成值
【Entity Framework】如何使用EF中的生成值 文章目录 【Entity Framework】如何使用EF中的生成值一、概述二、默认值三、计算列四、设置主键五、显示配置值生成六、设置日期/时间值生成6.1 创建时间戳6.2 更新时间戳 七、替代值生成八、无值生成九、总结 一、概述 数据库列的值…...

【MATLAB源码-第185期】基于matlab的16QAM系统相位偏移估计EOS算法仿真,对比补偿前后的星座图误码率。
操作环境: MATLAB 2022a 1、算法描述 1. 引言 M-QAM调制技术的重要性 现代通信系统追求的是更高的数据传输速率和更有效的频谱利用率。M-QAM调制技术,作为一种高效的调制方案,能够通过在相同的带宽条件下传输更多的数据位来满足这一需求…...

C++入门语法(命名空间缺省函数函数重载引用内联函数nullptr)
目录 前言 1. 什么是C 2. C关键字 3. 命名空间 3.1 命名空间的定义 3.2 命名空间的使用 4. C输入和输出 5. 缺省函数 5.1 概念 5.2 缺省参数分类 6. 函数重载 6.1 概念 6.2 为何C支持函数重载 7. 引用 7.1 概念 7.2 特性 7.3 常引用 7.4 引用与指针的区别 7…...
9.vector的使用介绍和模拟实现
1.vector的介绍及使用 1.1 vector的介绍 vector的文档介绍 vector是表示可变大小数组的序列容器。 就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素进行访问,和数组一样高效。但是又不像数组,…...

探索设计模式的魅力:MVVM模式在AI大模型领域的创新应用-打破传统,迎接智能未来
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,坚持默默的做事。 MVVM模式在AI大模型领域的创新应用-打破传统迎接智能未来 🚀 “在人工智能的领域里&a…...
Docker使用— Docker部署安装Nginx
Nginx简介 Nginx 是一款高性能的 web 服务器、反向代理服务器以及电子邮件(IMAP/POP3/SMTP)代理服务器,由俄罗斯开发者伊戈尔塞索耶夫(Igor Sysoev)编写,并在2004年10月4日发布了首个公开版本0.1.0。Nginx…...
C/C++基础----运算符
算数运算符 运算符 描述 例子 两个数字相加 两个变量a b得到两个变量之和 - 两个数字相减 - * 两个数字相乘 - / 两个数字相除 - % 两个数字相除后取余数 8 % 3 2 -- 一个数字递减 变量a:a-- 、--a 一个数字递增 变量a: a 、 a 其中递…...

YOLOv9:下一代目标检测的革新
目标检测作为计算机视觉领域的一个重要分支,一直是研究的热点。YOLO系列作为目标检测算法的佼佼者,自YOLO1发布以来,就在速度和精度上取得了很好的平衡,深受业界和学术界的喜爱。 YOLOv9作为该系列的最新版本,不仅在性…...
Leetcode算法训练日记 | day20
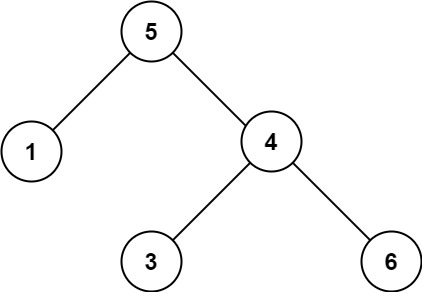
一、合并二叉树 1.题目 Leetcode:第 617 题 给你两棵二叉树: root1 和 root2 。 想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...