matlab基础到实战(1)
目录
- 概述
- sin函数例子
- 四则运算
- 实数
- 复数
- 逻辑运算
- 复数运算
- 模
- 幅角
- 共轭
- 向量
- 二维向量定义
- 序列生成向量
- 向量索引方式
- 加减乘除
- 向量间运算
- 加减
- 乘法
- 除法
概述
MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理、量化金融与风险管理、机器人,控制系统等领域。 [1]
MATLAB是matrix&laboratory两个词的组合,意为矩阵工厂(矩阵实验室),软件主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式。
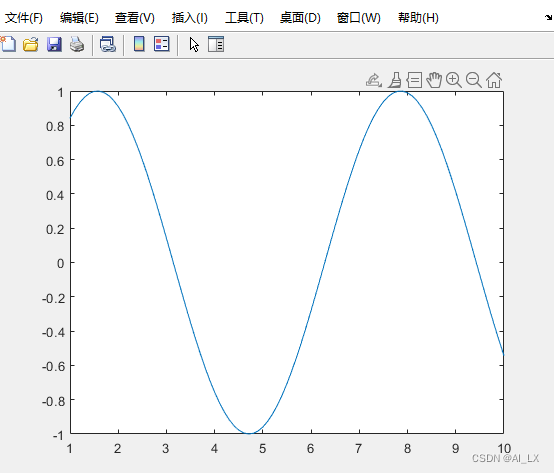
sin函数例子
>> x=1:0.1:10x =列 1 至 131.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000 2.1000 2.2000列 14 至 262.3000 2.4000 2.5000 2.6000 2.7000 2.8000 2.9000 3.0000 3.1000 3.2000 3.3000 3.4000 3.5000列 27 至 393.6000 3.7000 3.8000 3.9000 4.0000 4.1000 4.2000 4.3000 4.4000 4.5000 4.6000 4.7000 4.8000列 40 至 524.9000 5.0000 5.1000 5.2000 5.3000 5.4000 5.5000 5.6000 5.7000 5.8000 5.9000 6.0000 6.1000列 53 至 656.2000 6.3000 6.4000 6.5000 6.6000 6.7000 6.8000 6.9000 7.0000 7.1000 7.2000 7.3000 7.4000列 66 至 787.5000 7.6000 7.7000 7.8000 7.9000 8.0000 8.1000 8.2000 8.3000 8.4000 8.5000 8.6000 8.7000列 79 至 918.8000 8.9000 9.0000 9.1000 9.2000 9.3000 9.4000 9.5000 9.6000 9.7000 9.8000 9.9000 10.0000>> y=sin(x)y =列 1 至 130.8415 0.8912 0.9320 0.9636 0.9854 0.9975 0.9996 0.9917 0.9738 0.9463 0.9093 0.8632 0.8085列 14 至 260.7457 0.6755 0.5985 0.5155 0.4274 0.3350 0.2392 0.1411 0.0416 -0.0584 -0.1577 -0.2555 -0.3508列 27 至 39-0.4425 -0.5298 -0.6119 -0.6878 -0.7568 -0.8183 -0.8716 -0.9162 -0.9516 -0.9775 -0.9937 -0.9999 -0.9962列 40 至 52-0.9825 -0.9589 -0.9258 -0.8835 -0.8323 -0.7728 -0.7055 -0.6313 -0.5507 -0.4646 -0.3739 -0.2794 -0.1822列 53 至 65-0.0831 0.0168 0.1165 0.2151 0.3115 0.4048 0.4941 0.5784 0.6570 0.7290 0.7937 0.8504 0.8987列 66 至 780.9380 0.9679 0.9882 0.9985 0.9989 0.9894 0.9699 0.9407 0.9022 0.8546 0.7985 0.7344 0.6630列 79 至 910.5849 0.5010 0.4121 0.3191 0.2229 0.1245 0.0248 -0.0752 -0.1743 -0.2718 -0.3665 -0.4575 -0.5440>> plot(x,y)
四则运算
实数
>> x=[1 2 3]x =1 2 3>> x*2ans =2 4 6>> x+6ans =7 8 9>> x-9ans =-8 -7 -6>> x/3ans =0.3333 0.6667 1.0000>>
复数
>> x=11+9ix =11.0000 + 9.0000i>> y=9-6iy =9.0000 - 6.0000i>> x-yans =2.0000 +15.0000i>> x+yans =20.0000 + 3.0000i>> x*yans =1.5300e+02 + 1.5000e+01i>> y/xans =0.2228 - 0.7277i>>
逻辑运算
>> %逻辑与,两个操作数同时为1时,结果为1,否则为0
>> and(11,0)ans =logical0>> and(-11,0)ans =logical0>> %逻辑或,两个操作其中至少一个为1时,结果为1,否则为0
>> or(11,0)ans =logical1>> or(-11,0)ans =logical1>> or(0,0)ans =logical0>>
>>> %逻辑非,当操作数为0时,结果为1,否则为0
>> ~ 11ans =logical0>> ~ 0ans =logical1>>
>>> %逻辑异或,相同时为0,不同时为1
>> xor(0,1)ans =logical1>> xor(11,11)ans =logical0>>
>>> %有非零元素为真,为1,否则为0
>> any([11 22 0 -11])ans =logical1>> any([0 0 0 0])ans =logical0>>
>>> %所有元素非零为真,为1,否则为0
>> all([11,22,44,0])ans =logical0>> all([11,22,0,0])ans =logical0>> all([11,22,10,110])ans =logical1>>
%表示注释
复数运算
>> a=12-9ia =12.0000 - 9.0000i
或者下面这种方式定义
>> complex(12,-9)ans =12.0000 - 9.0000i
模
>> abs(a)ans =15
幅角
>> angle(a)ans =-0.6435>>
共轭
实数部分
>> real(a)ans =12
虚数部分
>> imag(a)ans =-9
共轭复数
>> conj(a)ans =12.0000 + 9.0000i如果单个复数或复数矩阵中的虚部为0,则为实数矩阵
>> a=11-9ia =11.0000 - 9.0000i>> b=9+0ib =9>> c=0-1i
c =0.0000 - 1.0000i>> isreal(a)ans =logical0>> isreal(b)ans =logical1>> isreal(c)ans =logical0
向量
二维向量定义
>> x=[1,2;3,4]x =1 23 4>> x=[1 2; 3 4]x =1 23 4
序列生成向量
>> x=[1:10]x =1 2 3 4 5 6 7 8 9 10>> x=[1:3:12]%相差3生成序列x =1 4 7 10
>> x=linspace(1,10,3)%定义元素个数,linspace(第一个元素,最后一个元素,元素个数)x =1.0000 5.5000 10.0000
>> x=logspace(1,5,3)%定义元素个数,linspace(a,b,元素个数),10^a为第一个元素,10^b为最后一个元素x =10 1000 100000>> xx =10 1000 100000向量索引方式
注意从1开始,不从0开始。
>> x(1)ans =10>> x(1:2)ans =10 1000>> x(2:3)ans =1000 100000>> x(0)
数组索引必须为正整数或逻辑值。
加减乘除
每个元素进行
>> x=linspace(1,12,4)x =1.0000 4.6667 8.3333 12.0000>> y=linspace(3,15,4)y =3 7 11 15>> x/2ans =0.5000 2.3333 4.1667 6.0000>> x*2ans =2.0000 9.3333 16.6667 24.0000>> x+2ans =3.0000 6.6667 10.3333 14.0000>> x-2ans =-1.0000 2.6667 6.3333 10.0000向量间运算
加减
每个对应元素进行
>> xx =1.0000 4.6667 8.3333 12.0000>> yy =3 7 11 15>> x+yans =4.0000 11.6667 19.3333 27.0000>> x-yans =-2.0000 -2.3333 -2.6667 -3.0000
乘法
1、向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
两个向量a和b的叉积写作a×b
向量积可以被定义为:
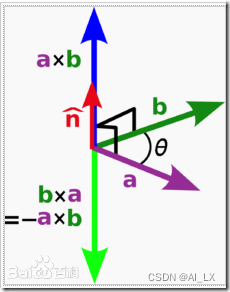
模长:(在这里θ表示两向量之间的夹角(共起点的前提下)(0°≤θ≤180°),它位于这两个矢量所定义的平面上。)
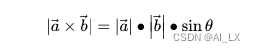
方向:a向量与b向量的向量积的方向与这两个向量所在平面垂直,且遵守右手定则。c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。
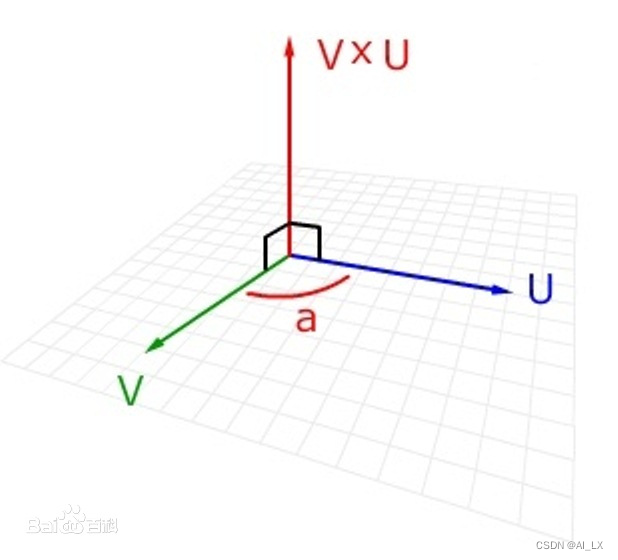
>> xx =1 3 5>> yy =10 12 14>> cross(x,y)ans =-18 36 -182、点积
点积在数学中,又称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。


>> xx =1.0000 4.6667 8.3333 12.0000>> y'ans =371115>> x*y'ans =307.3333>> x=[1:2:6]x =1 3 5>> y=[10:2:15]y =10 12 14>> dot(x,y)ans =116>> x*y'ans =1163、点乘与点除
每个元素进行
>> xx =1 3 5>> yy =10 12 14>> x.*yans =10 36 70
>> y./xans =10.0000 4.0000 2.8000
除法
在两个向量平行时才有除法
>> x=[1 4]x =1 4>> y=[6 24]y =6 24>> y/xans =6>> x/yans =0.1667
cross
叉积
语法
matlab C = cross(A,B) C = cross(A,B,dim)说明
C = cross(A,B)返回 A 和 B 的叉积。如果 A 和 B 为向量,则它们的长度必须为 3。
如果 A 和 B 为矩阵或多维数组,则它们必须具有相同大小。在这种情况下,cross 函数将 A 和 B 视为三元素向量集合。该函数计算对应向量沿大小等于 3 的第一个数组维度的叉积。
C = cross(A,B,dim)计算数组 A 和 B 沿维度 dim 的叉积。A 和 B 必须具有相同的大小,并且 size(A,dim) 和 size(B,dim) 必须为 3。dim 输入是一个正整数标量。
dim - 沿其运算的维度
正整数标量
沿其运算的维度,指定为正整数标量。维度 dim 的大小必须为 3。如果未指定值,则默认值是大小等于 3 的第一个数组维度。
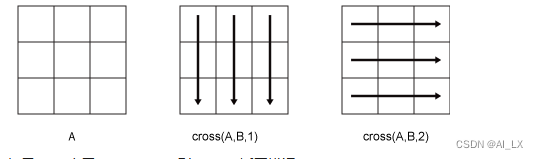
考虑两个二维输入数组:A 和 B:
cross(A,B,1) 将 A 和 B 的列视为向量,并返回对应列的叉积。
cross(A,B,2) 将 A 和 B 的行视为向量,并返回对应行的叉积。
如果 dim 大于 ndims(A),则 cross 返回错误。
相关文章:

matlab基础到实战(1)
目录概述sin函数例子四则运算实数复数逻辑运算复数运算模幅角共轭向量二维向量定义序列生成向量向量索引方式加减乘除向量间运算加减乘法除法概述 MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理…...

谷歌发布编写分布式应用的框架Service Weaver
一个新的框架,在本地以模块化单体的形式运行,一旦部署,则为分布式微服务架构 转载请注明来源:https://janrs.com/2023/03/%e8%b0%b7%e6%ad%8c%e5%8f%91%e5%b8%83%e7%bc%96%e5%86%99%e5%88%86%e5%b8%83%e5%bc%8f%e5%ba%94%e7%94%a8…...
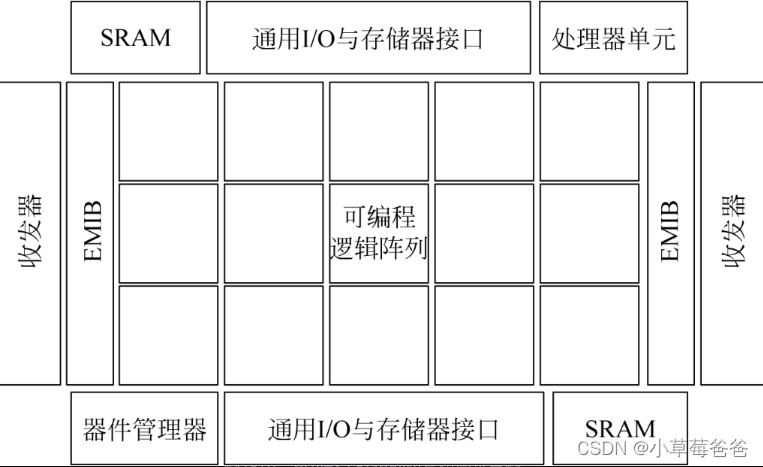
详解FPGA:人工智能时代的驱动引擎观后感
详解FPGA:人工智能时代的驱动引擎观后感 本书大目录 第一章 延续摩尔定律 第二章 拥抱大数据的洪流 第三章 FPGA在人工智能时代的独特优势 第四章 更简单也更复杂——FPGA开发的新方法 第五章 站在巨人肩上——FPGA发展新趋势 文章目录详解FPGA:人工智能…...

Rest/Restful接口
Rest Rest的全称是Representational State Transfer 。Rest是一种架构风格。Rest有很多原则和限制: 客户端-服务端架构模式无状态可缓存统一接口分层系统按需缓存 Rest对我们开发人员来说基本上就是资源,我们一般通过URI表示我们请求的一个资源。例如:…...
【vue init】三.项目引入axios、申明全局变量、设置跨域
教程目录 一:《【vue init】使用vue init搭建vue项目》 二:《【vue init】项目使用vue-router,引入ant-design-vue的UI框架,引入less》 三:《【vue init】项目引入axios、申明全局变量、设置跨域》 根据前文《【vue init】项目使…...

搭建nextcloud私有云盘
要搭建Nextcloud,需要在服务器上安装和配置Nginx、PHP和SQLite3。下面是一些基本步骤: 安装Nginx 可以使用包管理器进行安装。例如,在Ubuntu上可以运行以下命令: sudo apt update sudo apt install nginx配置Nginxwget -P /home/u…...
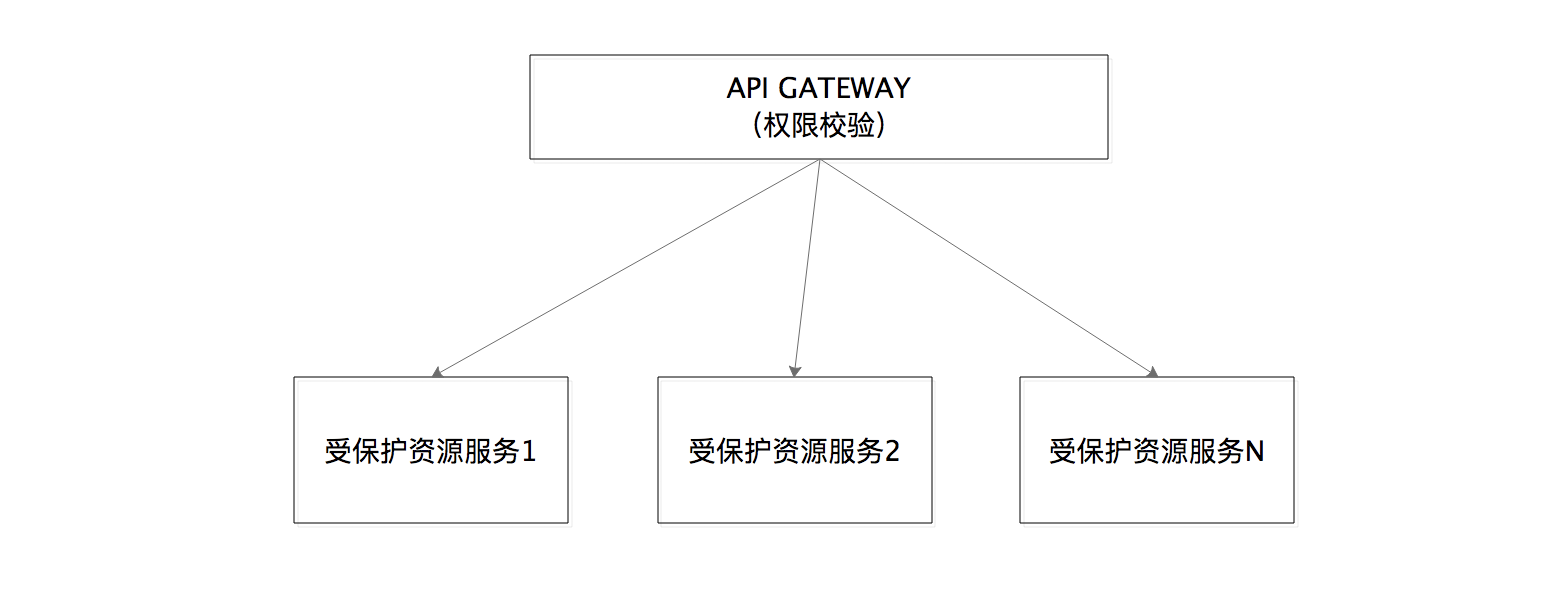
05 | 如何安全、快速地接入OAuth 2.0?
05 | 如何安全、快速地接入OAuth 2.0? 构建第三方软件应用 第一点,注册信息 小兔软件的研发人员提前登录到京东商家开放平台进行手动注册,以便后续使用这些注册的相关信息来请求访问令牌。兔软件需要先拥有自己的 app_id 和 app_serect 等信…...

nest.js学习笔记(一)
nest.js学习笔记(一)一、安装nest.js前置条件运行项目目录介绍二、nest.js cli 常用命令三、RESTful 风格设计1.接口url2.RESTful 版本控制四、获取前端传过来的参数1.获取Get请求参数2.获取Post请求参数3.动态路由4.获取Header信息5.自定义状态码nest.j…...
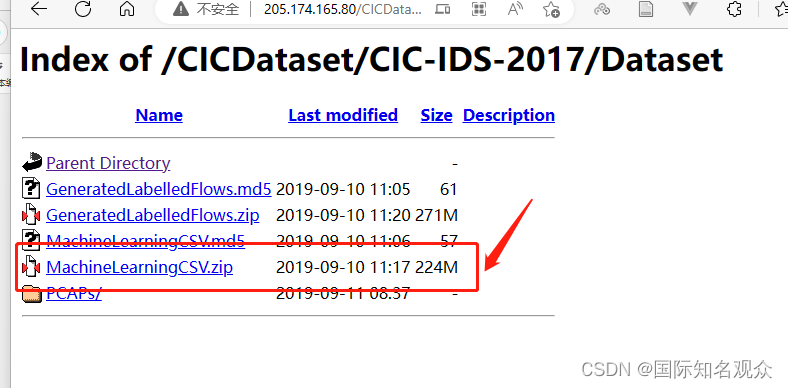
win下载配置CIC Flowmeter环境并提取流量特征
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录前言一、下载CIC Flowmeter二、安装java、maven、gradle和IDEA1.java 1.82.maven3.gradle4.IDEA三、CICFlowMeter-master使用四、流量特征1.含义2.获取前言 配了一整…...

【LeetCode刷题-Java/Python】二分查找
二分查找704.二分查找题目实现总结35.搜索插入位置题目实现34. 在排序数组中查找元素的第一个和最后一个位置题目实现69.x的平方根题目实现367. 有效的完全平方数题目实现704.二分查找 题目 题目链接 给定一个 n 个元素有序的(升序)整型数组 nums 和一…...

Linux 6.2 已正式发布
Linus Torvalds 发布了稳定的 Linux 6.2 内核,这是 2023 年的第一个主要内核版本。硬件方面,Linux 6.2 提升了 Intel Arc 显卡 (DG2/Alchemist) 的稳定性,真正做到开箱即用。英特尔的 On Demand 驱动程序现在状态良好,适用于第 4 …...

Kubernetes 101,第一部分,基础知识
已经有一段时间了,我想花点时间坐下来写写关于Kubernetes 的文章。时机已到。 简而言之,Kubernetes是一个用于自动化和管理容器化应用程序的开源系统。Kubernetes 就是关于容器的。 ❗如果你对什么...
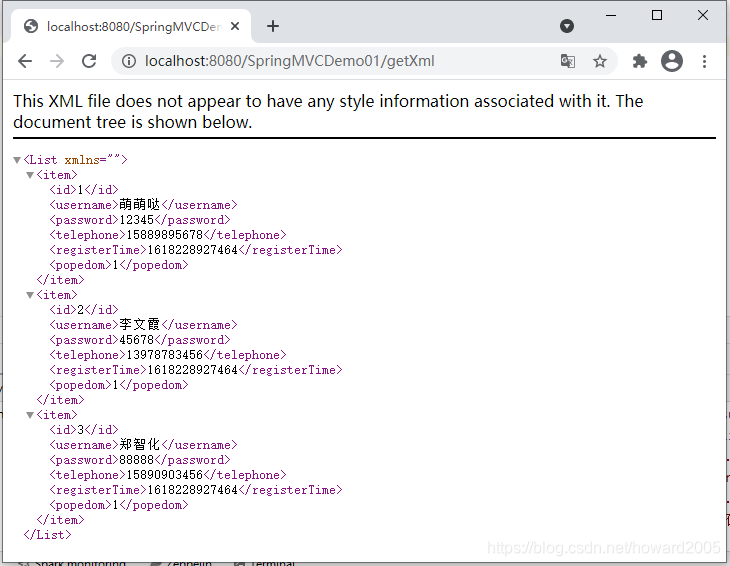
企业级信息系统开发学习笔记1.7 基于XML配置方式使用Spring MVC
文章目录零、本节学习目标一、Spring MVC概述1、MVC架构2、Spring MVC3、使用Spring MVC的两种方式二、基于XML配置与注解的方式使用Spring MVC(一)创建Spring项目【SpringMVCDemo01】(二)在pom文件里添加相关依赖(三&…...

java反射,动态代理
1. 反射 1.1 反射的概述: 专业的解释(了解一下): 是在运行状态中,对于任意一个类,都能够知道这个类的所有属性和方法; 对于任意一个对象,都能够调用它的任意属性和方法…...
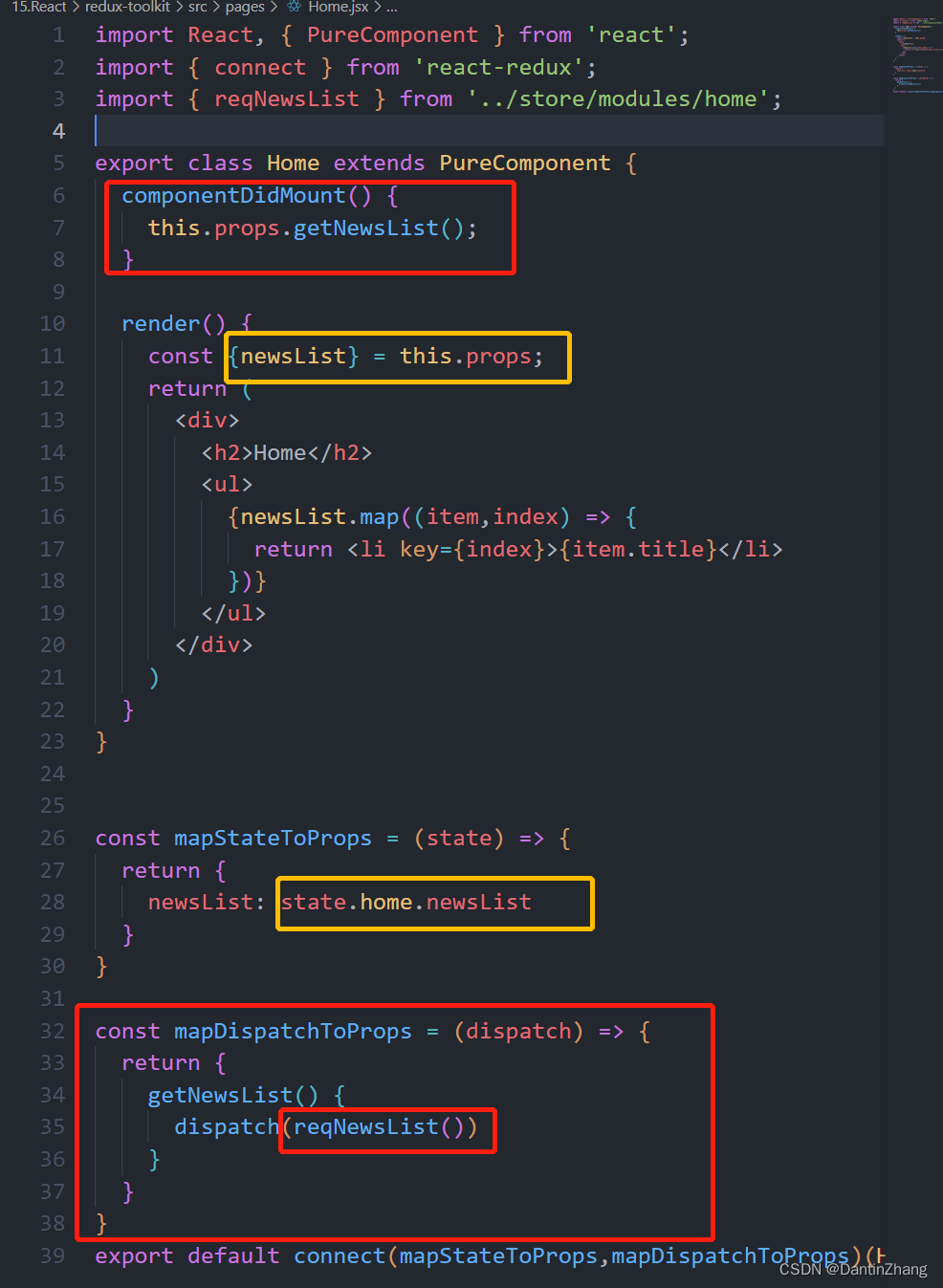
React(六):Redux的使用、react-redux简化代码、redux模块化、RTK的使用
React(六)一、Redux测试项目搭建1.创建store仓库2.创建reducer函数(纯函数)3.constants.js保存action名字4.修改store中的数据5.动态生成action二、React中如何使用redux1.安装redux2.创建store3.组件中订阅store4.派发action修改…...

静态库和动态库的打包与使用
静态库和动态库 静态库和动态库的打包 生成可执行程序时链接使用 运行可执行程序时加载使用 提前声明,笔者示例的文件有mian.c/child.c/child.h。OK,我们先了解一下,库文件是什么?它其实就是打包了一堆实现常用功能的代码文件. ⭐…...

h264编码之SPS解析
一、概念 SPS即Sequence Paramater Set,又称作序列参数集。SPS中保存了一组编码视频序列(Coded video sequence)的全局参数。 二、定义 H.264标准协议中规定的SPS格式位于文档的7.3.2.1.1,如下图所示: 1、profile_idc 根据《T-REC-H.264-2…...

使用R语言包clusterProfiler做KEGG富集分析时出现的错误及解决方法
使用enrichKEGG做通路富集分析时,一直报错:显示No gene can be mapped....k <- enrichKEGG(gene gene, organism "hsa", pvalueCutoff 1, qvalueCutoff 1)但是之前用同样的基因做分析是能够成功地富集到通路,即便是网上的数据…...
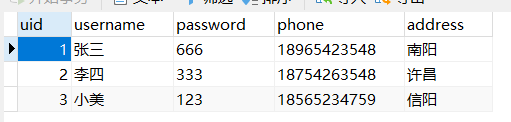
框架——MyBatis的入门案例
框架概述1.1什么是框架框架(Framework)是整个或部分系统的可重用设计,表现为一组抽象构件及构件实例间交与的方法;另一种定义认为,框架是可被应用开发者定制的应用骨架。前者是从应用方面而后者是从目的方面给出的定义…...

hadoop兼容性验证
前言 Hadoop是一个由Apache基金会所开发的分布式系统基础架构,主要解决海量数据的存储和海量数据的分析计算问题,广义上来说,Hadoop通常是指一个更广泛的概念–hadoop生态圈 Hadoop优缺点: 优点: 1、高可靠性&#x…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
