选择排序解读
在计算机科学中,排序算法是一种将数据元素按照某种顺序排列的算法。今天,我们要探讨的是选择排序(Selection Sort),这是一种简单直观的排序方法,通过不断选择剩余元素中的最小(或最大)元素,放到已排序序列的末尾,直到全部待排序的数据元素排完。
一、算法原理
选择排序的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。选择排序是不稳定的排序方法。
具体步骤如下:
- 在未排序序列中找到最小(或最大)元素,存放到排序序列的起始位置。
- 再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾。
- 以此类推,直到所有元素均排序完毕。

二、代码实现
以下是使用Python语言实现选择排序的示例代码:
def selection_sort(arr): # 遍历所有数组元素 for i in range(len(arr)): # 找到当前未排序部分的最小元素的下标 min_idx = i for j in range(i+1, len(arr)): if arr[j] < arr[min_idx]: min_idx = j # 将找到的最小元素和第一个未排序的元素交换位置 arr[i], arr[min_idx] = arr[min_idx], arr[i] return arr # 示例
arr = [64, 25, 12, 22, 11]
print("原始数组:", arr)
sorted_arr = selection_sort(arr)
print("排序后的数组:", sorted_arr)
三、算法分析
选择排序的时间复杂度为O(n^2),其中n为待排序元素的数量。这是因为它包含两个嵌套的循环:外层循环遍历所有元素,内层循环用于查找当前未排序部分的最小元素。因此,尽管选择排序在某些情况下可能不是最高效的排序方法,但由于其实现简单且易于理解,它在教学和某些特定场景下仍然有其应用价值。
在空间复杂度方面,选择排序是原地排序,它只需要一个额外的空间来存储每次找到的最小元素的索引,因此其空间复杂度为O(1)。
四、优缺点
选择排序的优点是易于实现和理解,且不需要额外的存储空间(除了一个临时变量)。然而,它的缺点是时间效率较低,特别是在处理大规模数据时,其性能不如一些更先进的排序算法。
五、总结
选择排序是一种简单直观的排序方法,适用于小规模数据的排序。虽然它的时间效率不如某些更高级的排序算法,但在某些特定场景下,由于其实现简单和易于理解的特点,它仍然具有一定的应用价值。在实际应用中,我们需要根据具体的需求和数据特点来选择合适的排序算法。
相关文章:

选择排序解读
在计算机科学中,排序算法是一种将数据元素按照某种顺序排列的算法。今天,我们要探讨的是选择排序(Selection Sort),这是一种简单直观的排序方法,通过不断选择剩余元素中的最小(或最大࿰…...

Vue项目自动注入less、sass、scss、stylus全局变量
一、Vue2项目 // vue.config.js const path require(path) module.exports {css: {loaderOptions: {// 给 sass-loader 传递选项sass: {// / 是 src/ 的别名// 所以这里假设有 src/assets/style/var.sass 这个文件// 注意:在 sass-loader v8 中,这个选…...

DXP学习002-PCB编辑器的环境参数及电路板参数相关设置
目录 一,dxp的pcb编辑器环境 1,创建新的PCB设计文档 2,PCB编辑器界面 1)布线工具栏 2)公用工具栏 3)层标签栏 编辑 3,PCB设计面板 1)打开pcb设计面板 4,PCB观…...

Flutter 使用flutter_swiper_null_safety 实现轮播图
目录 引入flutter_swiper_null_safety 在pubspec.yaml文件中dependencies下添加以下依赖 然后执行命令进行下载 实现轮播图 引入flutter_swiper_null_safety 在pubspec.yaml文件中dependencies下添加以下依赖 flutter_swiper_null_safety: ^1.0.2 然后执行命令进行下载 flu…...
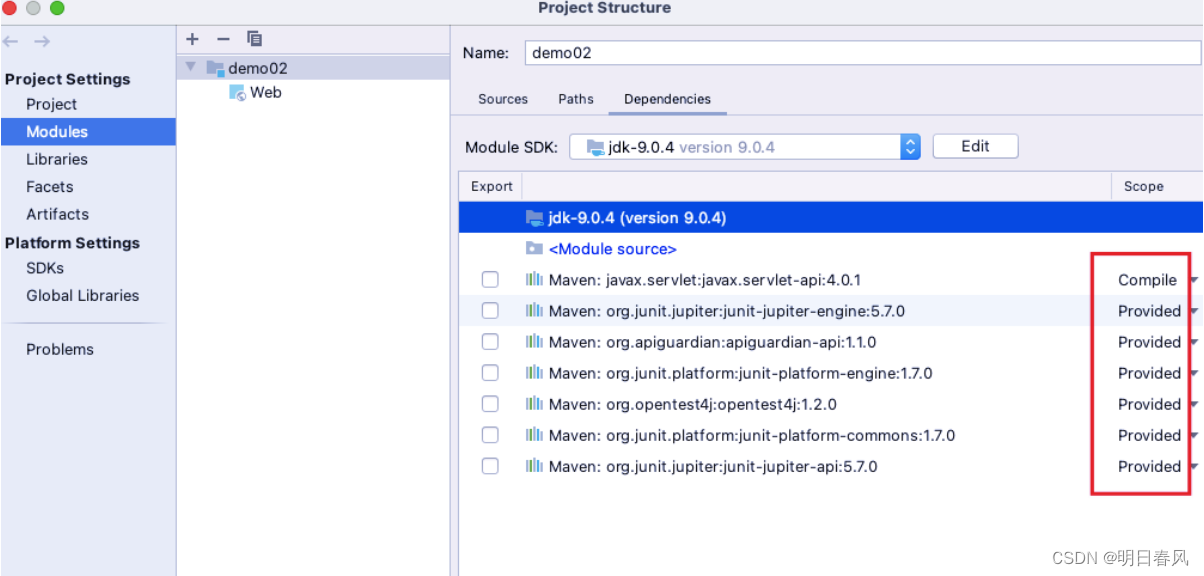
Maven的scope详解
依赖范围介绍 maven 项目不同的阶段引入到classpath中的依赖是不同的,例如,编译时,maven 会将与编译相关的依赖引入classpath中,测试时,maven会将测试相关的的依赖引入到classpath中,运行时,mav…...

如何修复在Deepin系统中因`apt-get autoremove systemd`导致的启动问题
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

LeetCode 每日一题 ---- 【2923. 找到冠军 I】
LeetCode 每日一题 ---- 【2923. 找到冠军 I】 2923.找到冠军I方法一:暴力求解 2923.找到冠军I 方法一:暴力求解 从头遍历一遍二维数组,如果发现 gird[x][y] 1,说明 x 队赢过 y 队,下面我们就只需要子再判断一下是否…...

CMakeLists常用命令
# 设置cmake最低版本 cmake_minimum_required(VERSION 3.2)# project命令用于指定cmake工程的名称,实际上,它还可以指定cmake工程的版本号(VERSION关键字)、 #简短的描述(DESCRIPTION关键字)、主页URL&…...

英语 倒装结构中的主语和助动词,用于强调 inversion
I am used to travelling by air and only on one occasion have I ever felt frightened. 1、翻译为中文:我习惯了乘坐飞机旅行,只有在一次经历中我感到过害怕。 2、分析时态和句子语法是否正确:该句子使用了现在完成时(I am u…...
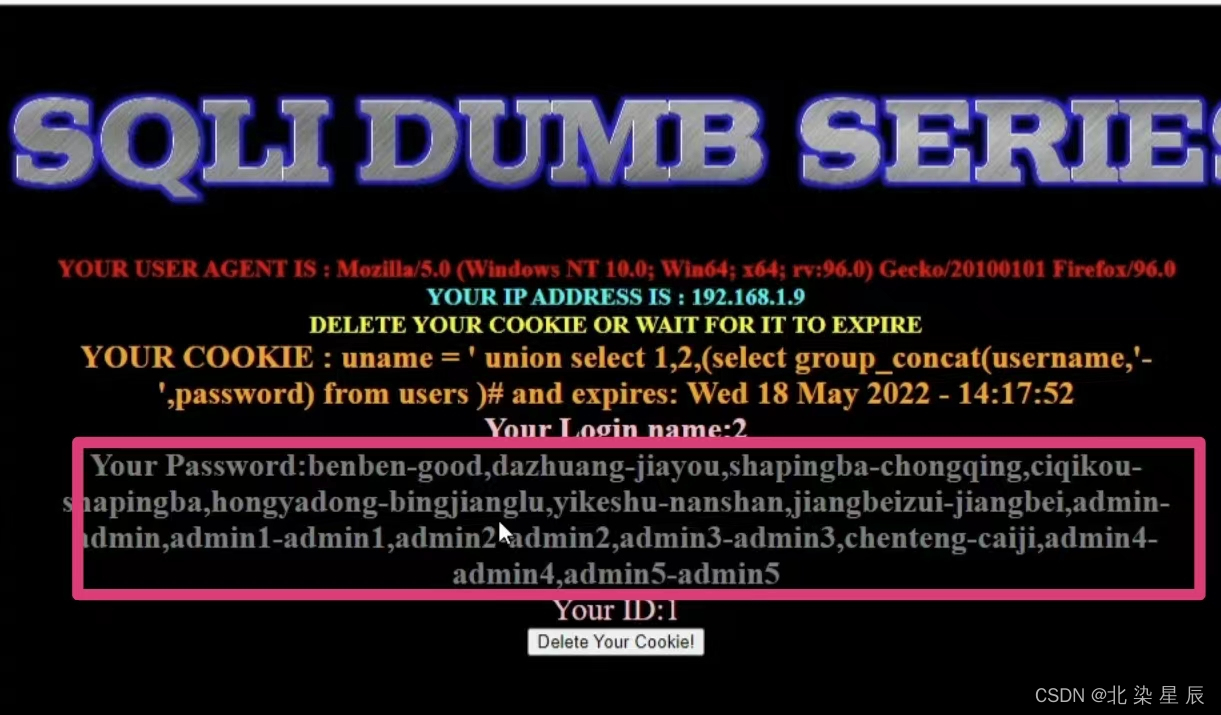
SQL注入---HTTP报头注入
文章目录 目录 文章目录 一.uagent注入 二.refeer注入 三.Cookie注入 前文中提到万能密钥的工作原理,然而万能密钥仅在源代码中没有代码审计,此时才被称之为万能密钥,而代码中有代码审计时需要分以下几种情况讨论 一.uagent注入 先看代码&a…...
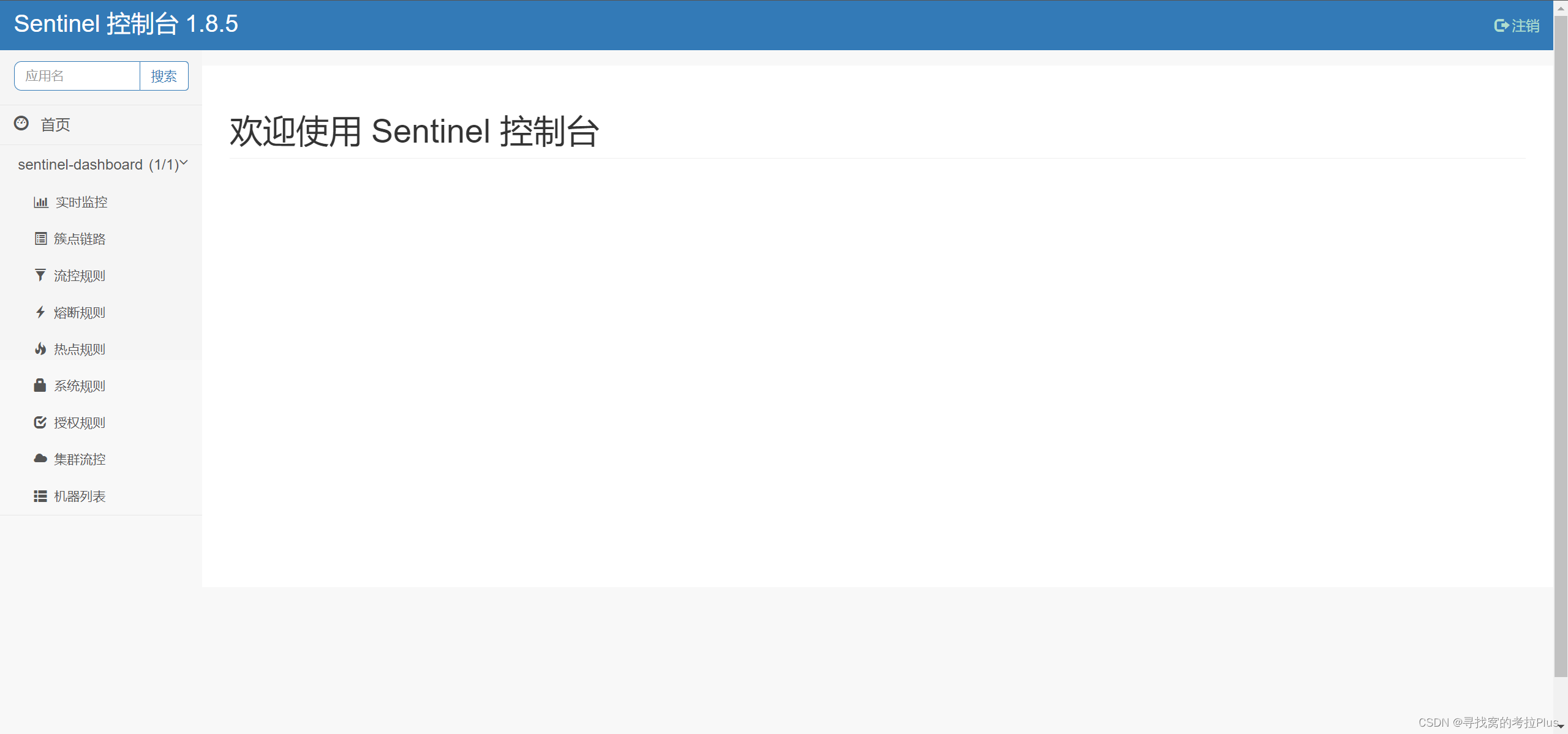
docker安装sentinel
文章目录 前言安装docker指令安装制作docker-compose.yaml文件 查看网站 前言 Sentinel 是阿里巴巴开源的一款轻量级流量控制和熔断降级工具,可用于保护分布式系统中的服务。它可以帮助开发人员解决在分布式架构中面临的流量管理、服务保护、性能优化等问题。 安装…...

达梦的归档日志参数ARCH_RESERVE_TIME测试
达梦的参数ARCH_RESERVE_TIME测试 前面有提到和oracle相比,达梦的归档日志相关参数有个比较特别,可以通过设置它去规定归档日志的保留时间。 ARCH_RESERVE_TIME:归档日志保留时间,单位分钟,取值范围 0~2147483647。只…...
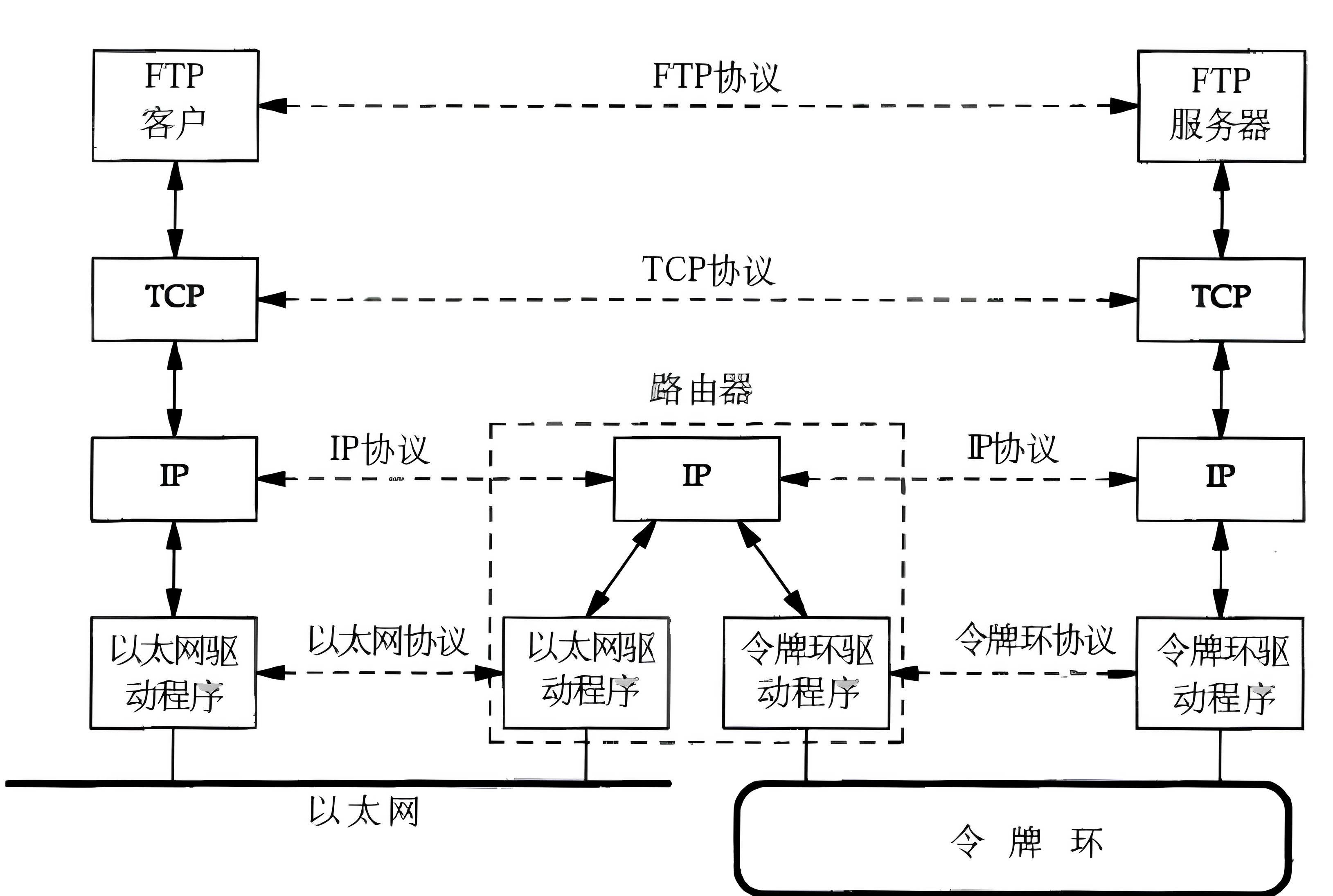
Linux网络 基础概念
目录 背景知识 互联网的发展 局域网和广域网 网络拓扑 网络协议栈 协议的概念 网络协议的分层 网络与操作系统的联系 网络传输的基本流程 IP地址和MAC地址 以太网通信 数据包的封装和分用 跨网段传输 背景知识 互联网的发展 计算机网络是计算机技术和通信技术相…...
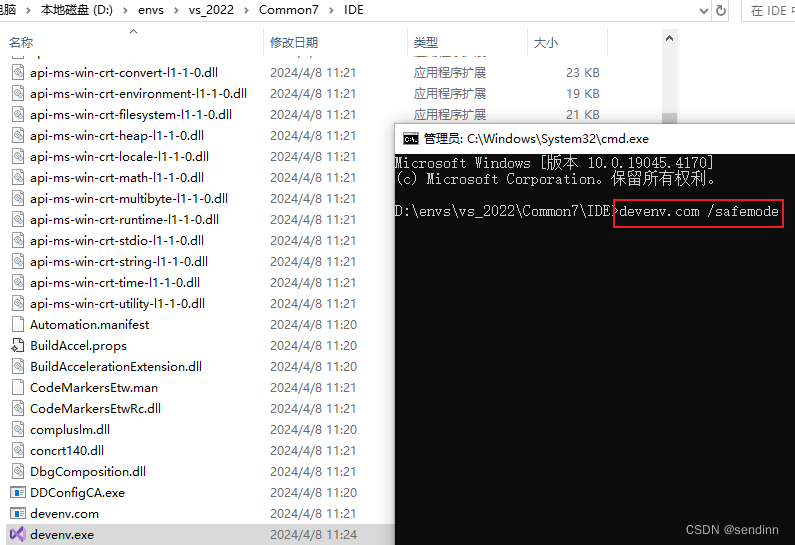
装机指导。
everything winrar snipaste cmake git tortoisegit tortoisesvn inno setup vs2022 安装的时候注意sdk路径一定要默认!! 否则你会发现在你的sdk安装路径的根盘符下会多出一个Windows Kits,强迫症接受不了 默认的会跟已有的装在一起…...
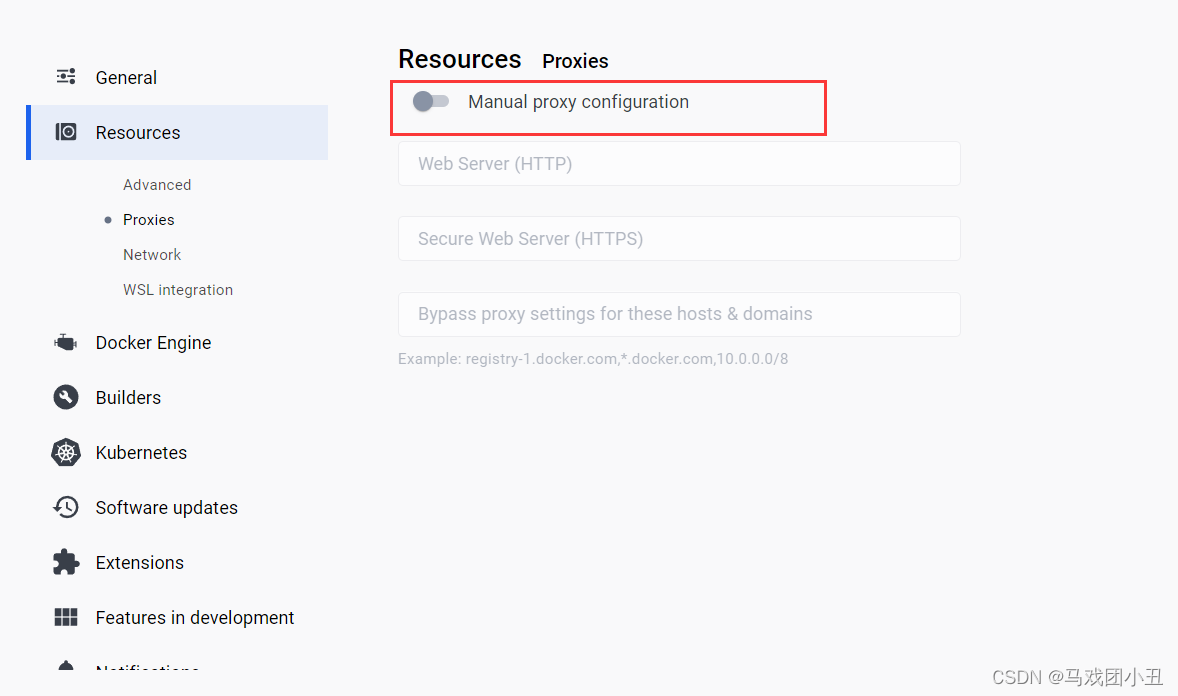
解决windows docker context deadline exceeded问题
首先确保开启了wsl。cmd 直接输wsl,进入虚拟命令行代表开启 配置镜像 内容如下: {"builder": {"gc": {"defaultKeepStorage": "20GB","enabled": true}},"experimental": false,"f…...
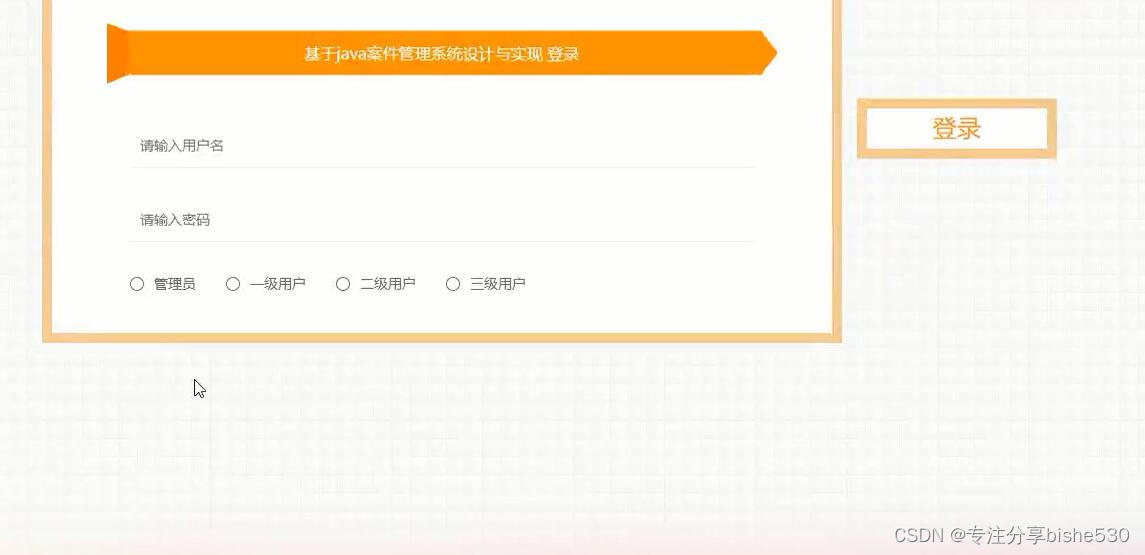
django基于python的法院执法案件管理系统
本课题使用Python语言进行开发。代码层面的操作主要在PyCharm中进行,将系统所使用到的表以及数据存储到MySQL数据库中,方便对数据进行操作本课题基于WEB的开发平台,设计的基本思路是: 框架:django/flask 后端ÿ…...

tcp early retransmit 和 rack 中神奇的 1/4 minrtt
雨中跑步十公里,沿河看柳,发了一则朋友圈: 为什么采用 1/4 minrtt 作为重传和探测的延时,上图解释的已经很清楚了,主要还是怕乱序,关于乱序的度量,上图解释得非常清楚,乱序预期可在…...
【强化学习实践】Gym+倒立单摆+创建自己的环境
一、Gym Gym是OpenAI开发的一个强化学习算法测试环境集合包。Gym提供了多种标准的环境,包括经典的游戏(如Atari游戏)、机器人模拟任务以及其他各种类型的问题,供开发者测试和训练强化学习智能体。在Gym环境中,开发者可…...
实习记录小程序|基于SSM的实习记录小程序设计与实现(源码+数据库+文档)
知识管理 目录 基于SSM的习记录小程序设计与实现 一、前言 二、系统设计 三、系统功能设计 1、小程序端: 2、后台 四、数据库设计 五、核心代码 六、论文参考 七、最新计算机毕设选题推荐 八、源码获取: 博主介绍:✌️大厂码农|毕…...
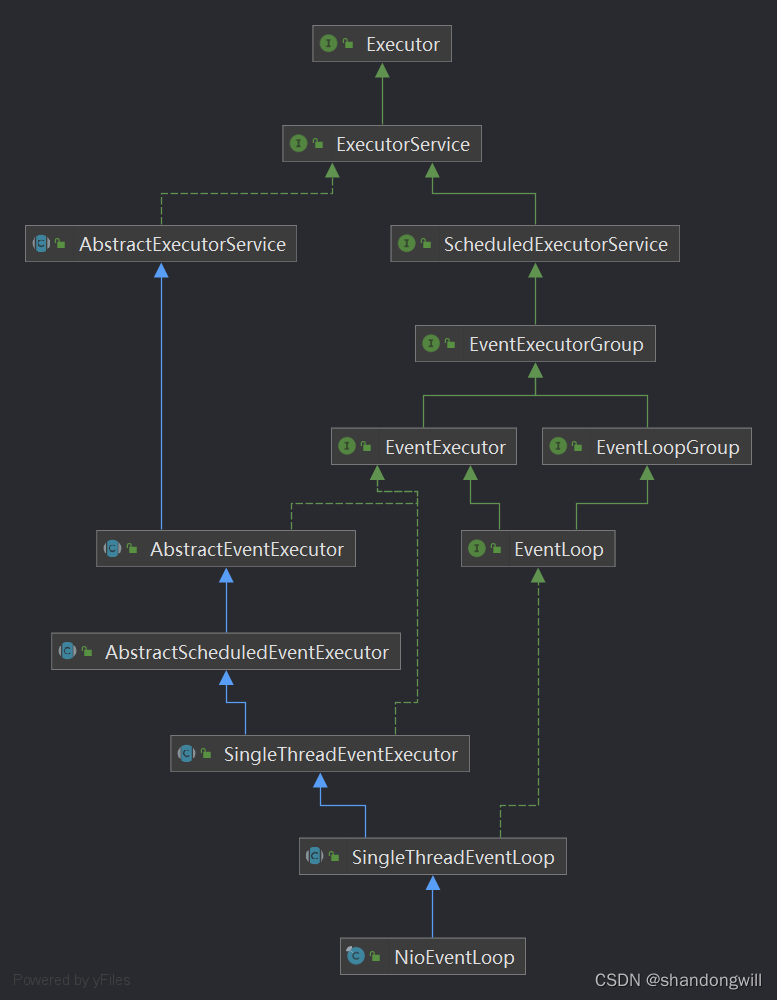
Netty NioEventLoop详解
文章目录 前言类图主要功能NioEventLoop如何实现事件循环NioEventLoop如何处理多路复用Netty如何管理Channel和Selector管理Channel管理Selector注意事项 前言 Netty通过事件循环机制(EventLoop)处理IO事件和异步任务,简单来说,就是通过一个死循环&…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
