leetcode热题100.爬楼梯(从二进制到快速幂)
Problem: 70. 爬楼梯
文章目录
- 题目
- 思路
- Code
- 复杂度
题目
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
思路
在上一讲从递归到动态规划中,我们讲解了递归和动态规划的求解思路,但是我们发现这两种方案的时间复杂度都为 o ( n ) o(n) o(n),我们试图找一种更加优秀的时间复杂度的解法
这里我们就要介绍快速幂的概念了
我们先将n表现为2进制,例如 3 13 3^{13} 313 = 3 1101 3^{1101} 31101 = 3 8 3^8 38 * 3 4 3^4 34 * 3 3 3
因为n有 ⌊ l o g 2 n ⌋ \lfloor log_2n \rfloor ⌊log2n⌋+1 个二进制位 当我们知道了 a 1 , a 2 , a 3 . . . . a^1,a^2,a^3.... a1,a2,a3....后我们只需要 o ( l o g n ) o(log n) o(logn)次乘法就可以计算出 a n a^n an了。
于是我们只需要知道一个快速的方法来计算上述 3 的 2 k 2^k 2k 次幂的序列。这个问题很简单,因为序列中(除第一个)任意一个元素就是其前一个元素的平方。例如:

那么对于我们刚才举得例子而言,我们只要计算得出 3 8 3^8 38 , 3 4 3^4 34 , 3 3 3,就可以得到其最后的真实值。
整个算法的时间复杂度是 0 ( l o g n ) 0(logn) 0(logn),比递归和递归都要优秀
回到本题,本题快速乘有一点不同,本题要用到矩阵 ,由上一篇从递归到动态规划中,我们已经知道了状态的递归公式:
f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n) = f(n-1) + f(n-2) f(n)=f(n−1)+f(n−2)
我们可以得到这样一个关系:
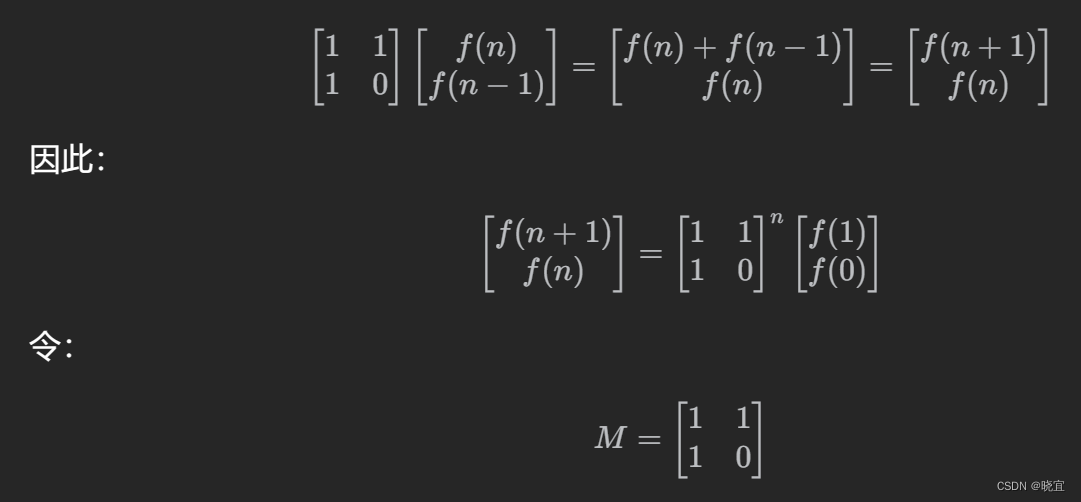
只要我们快速的求出矩阵的n次幂,那么我们就可以得出f(n),即最终答案。这里快速求解矩阵的方法,正是刚刚所讲的快速幂解法。
Code
class Solution {public int climbStairs(int n) {int[][] q = {{1,1},{1,0}};int[][] res = pow(q,n);return res[0][0];}public int[][] pow(int[][] a,int n){int[][] ret = {{1,0},{0,1}};while(n>0){if( (n&1)==1 ){ret = multiply(ret,a);}n >>= 1;a = multiply(a,a);}return ret;}public int[][] multiply(int[][] a,int[][] b){int[][] c = new int[2][2];for(int i=0;i<2;i++){for(int j=0;j<2;j++){c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];}}return c;}}
复杂度
时间复杂度:
只需要求 l o g ( n ) log(n) log(n)次, O ( l o g n ) O(logn) O(logn)
空间复杂度:
O ( 1 ) O(1) O(1)
相关文章:
leetcode热题100.爬楼梯(从二进制到快速幂)
Problem: 70. 爬楼梯 文章目录 题目思路Code复杂度 题目 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1: 输入:n 2 输出:2 解释:有两种方…...
使用Docker定时备份数据
文章目录 一、Docker镜像制作二、MySQL数据备份三、Minio数据备份四、数据跨服务器传输五、Nginx日志分割六、Docker启动七、Docker备份日志 一、Docker镜像制作 镜像制作目录 mc下载地址 - rsyncd.conf # https://download.samba.org/pub/rsync/rsyncd.conf.5port 873 uid …...

conda搭建与管理python环境
conda搭建与管理python环境.md Anaconda下载地址Miniconda下载地址Linux下安装1.执行安装2.查看可安装的python版本3.创建环境4.激活环境5.安装python的工具包5.退出环境6.删除指定的环境7.设置默认的环境 Window下安装1.执行安装2.配置环境变量3.检查是否安装成功4.通过conda配…...

获取当前的年、月、日、时、分、秒,并将这些信息用作保存 Excel 文件的前缀
要获取当前的年、月、日、时、分、秒,并将这些信息用作保存 Excel 文件的前缀,你可以使用 Python 的 datetime 模块来获取当前时间,并格式化时间字符串,然后使用 pandas 库将数据保存为 Excel 文件。示例代码: from d…...

Gitlab全量迁移
Gitlab全量迁移 一、背景1.前提条件 一、背景 公司研发使用的Gitlab由于服务器下架需要迁移到新的Gitlab服务器上。Gitlab官方推荐了先备份然后再恢复的方法。个人采用官方的另外一种方法,就写这篇文章给需要的小伙伴参考。 源Gitlab: http://old.mygitlab.com #地…...
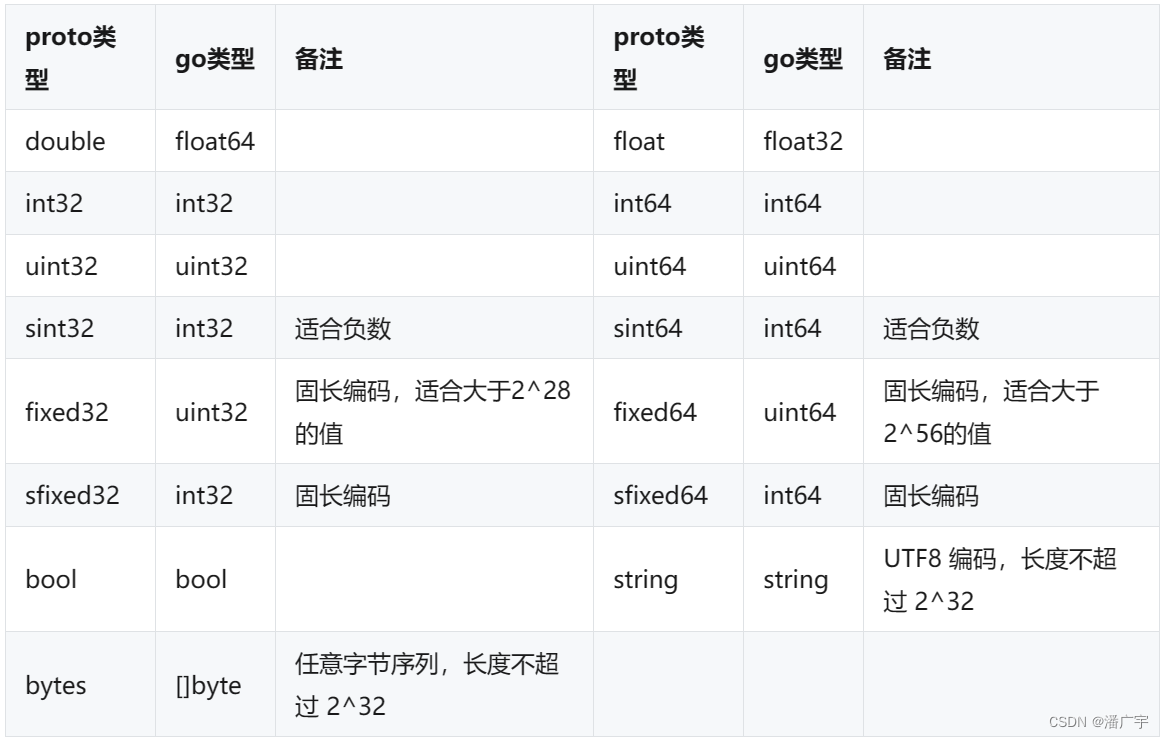
Golang ProtoBuf 初学者完整教程:语法
一、编码规范推荐 1、文件名使用小写下划线的命名风格,例如 lower_snake_case.proto 2、使用 2 个空格缩进 3、包名应该和目录结构对应 4、消息名使用首字母大写驼峰风格(CamelCase),例如message StudentRequest { ... } 5、字段名使用小写下划线的风格…...

使用.cc域名的优势
域名注册越来越难了,很多人选择结尾加123、56、365等等数字,总感觉怪怪的。那么能不能选择其他后缀的域名呢?我感觉可以,大部分用户都不会去看域名,只有做技术的会去关注。 使用.cc域名的优势 很多好域名,…...

存储器管理单元MMU概述
在ARM系统中,存储器管理单元MMU主要完成以下工作: ● 虚拟存储空间到物理存储空间的映射。在ARM中采用了页式虚拟存储管理。它把虚拟地址空间分成一个个固定大小的块,每一块称为一页,把物理内存的地址空间也分成同样大小的页。页…...
:网络拓扑管理,可视化监控网络,快速定位问题)
了解监控易(25):网络拓扑管理,可视化监控网络,快速定位问题
在复杂的网络环境中,快速准确地定位问题、确保网络的稳定运行是至关重要的。监控易的网络拓扑管理功能,正是为了解决这一问题而设计的。该功能通过可视化监控网络,帮助用户迅速把握网络整体状况,快速定位并解决问题。 监控易的网络…...

C#学习笔记10:winform上位机与西门子PLC网口通信_中篇_winform的窗口操作设计、日志的添加使用
今日继续我的C#winform上位机学习之路 这系列笔记的目标是尝试编写一个能够与西门子PLC进行以太网口通信的上位机软件。 文章提供完整代码解释、设计点解释、测试效果图、完整工程下载 本章主要学习:Winform多个窗体的一些操作 、无边框窗体的创建、Combox组件插…...
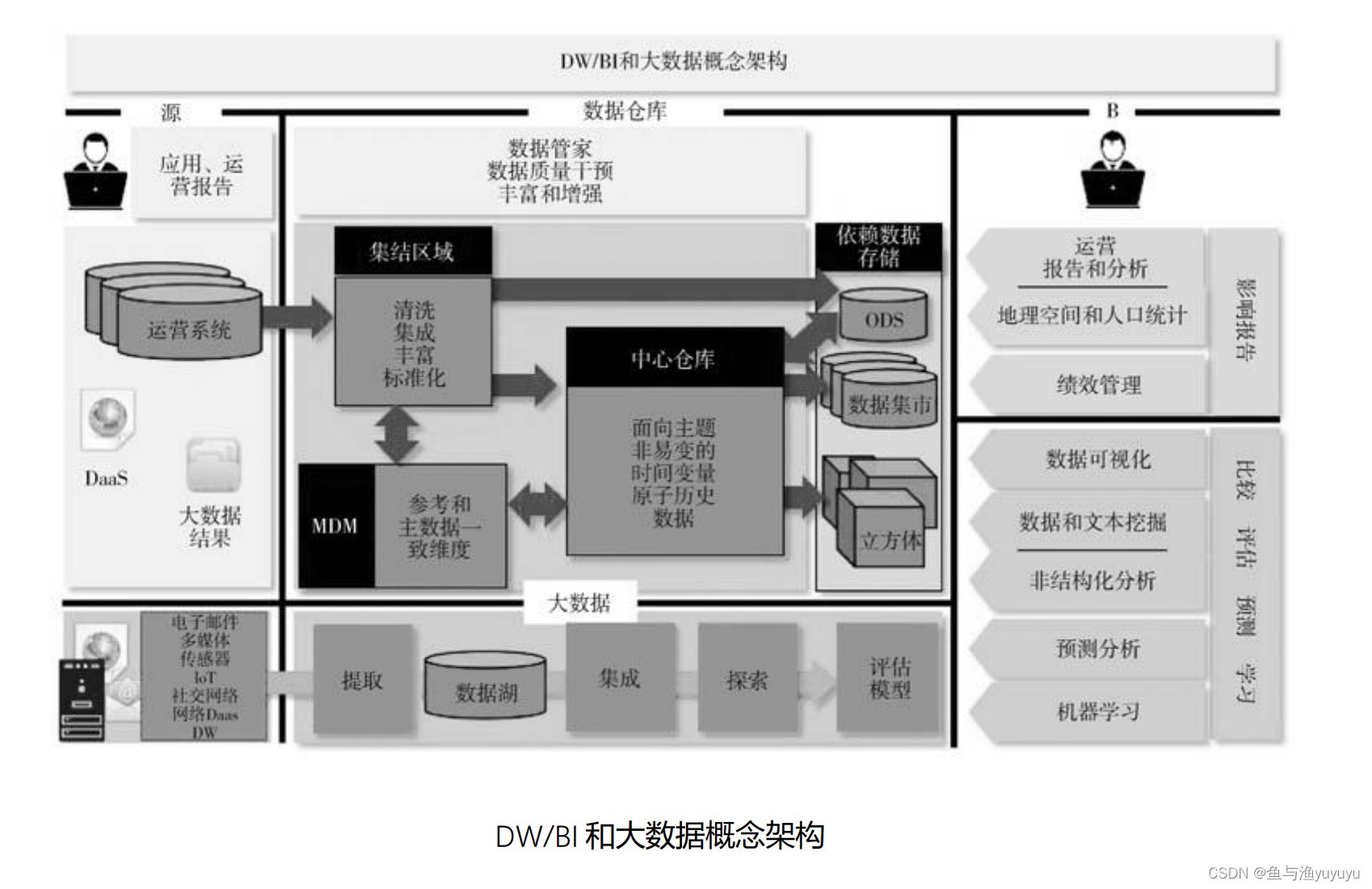
第14章 大数据与数据科学知识点梳理
第14章 大数据与数据科学知识点梳理(附带页码) ◼ 原则:组织应仔细管理与大数据源相关的元数据,以便对数据文件及其来源和价值进行准确的清单管理。P386 ◼ 大数据:数据量大(Volume)、数据更新…...
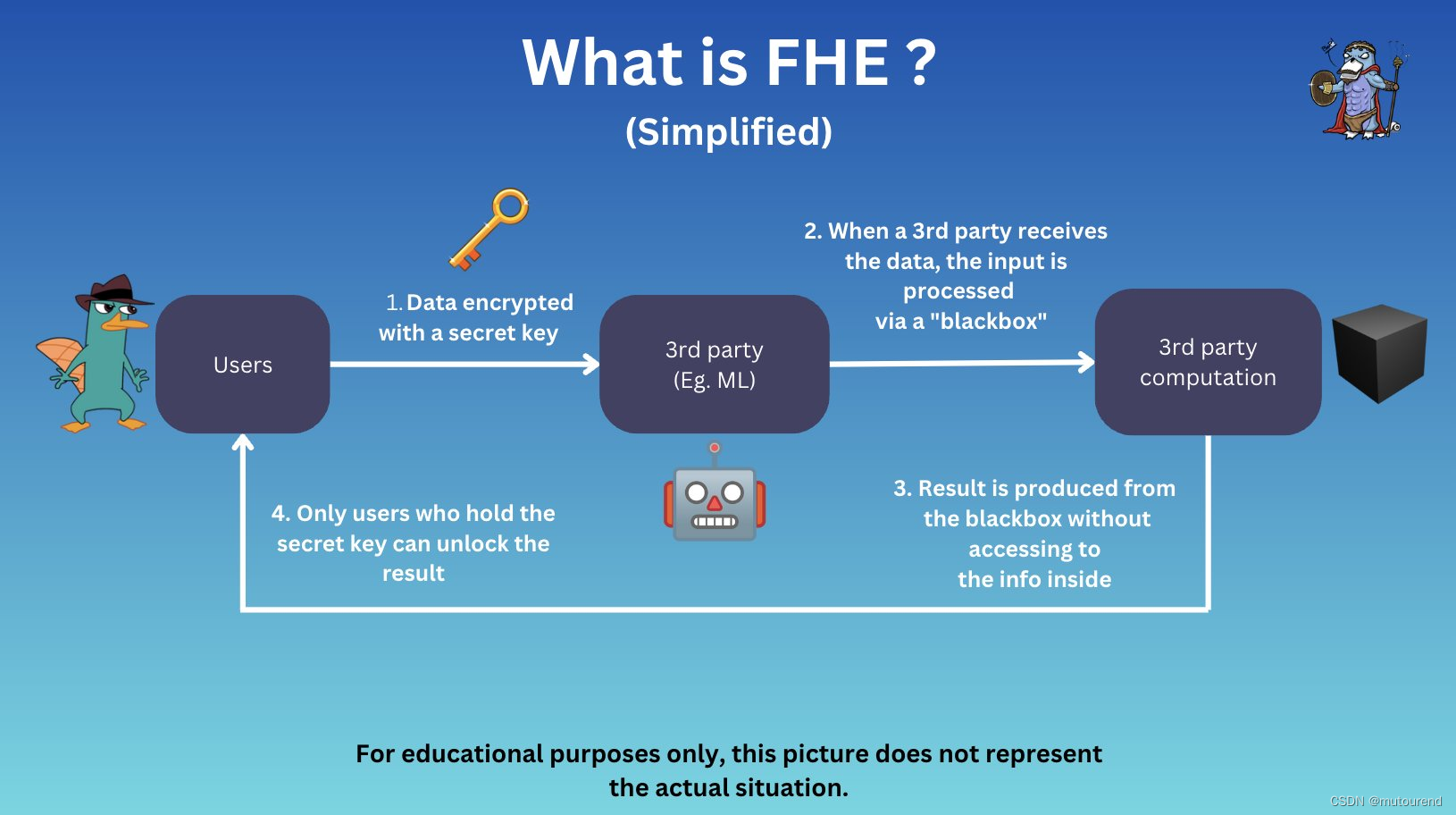
FHE全同态加密简介
1. 何为FHE? FHE (Fully homomorphic encryption): 是一种隐私技术,支持直接对密文进行计算,而无需对密文先解密再计算。即,任何第三方或云厂商,都可对敏感信息的密文进行处理,而无需访问密文内…...
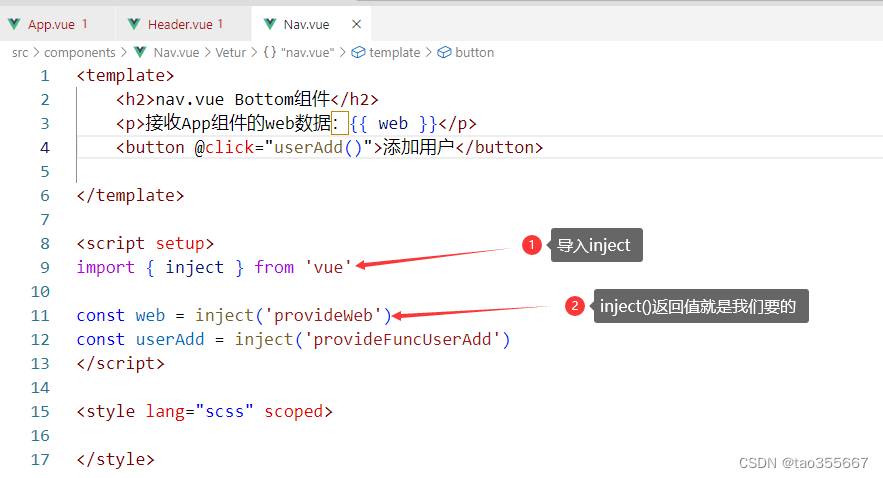
【vue】跨组件通信--依赖注入
import { provide,inject } from vue provide:将父组件的数据传递给所有子组件(子孙都有)inject:接收provide 项目文件结构 App.vue是Header.vue的父组件,Header.vue是Nav.vue的父组件 传值过程 App.vue <tem…...
Aritest+python+Jenkins解放双手iOS/Android自动化
ARITest、Python 和 Jenkins 可以结合在一起创建一个自动化测试解决方案,实现持续集成和持续测试的目标。以下是三者如何协同工作的基本概念: 1. **ARITest**: ARITest 是一款功能全面的自动化测试工具,提供 UI 自动化、接口自…...

Problem #7 [Medium]
This problem was asked by Facebook. Given the mapping a = 1, b = 2, … z = 26, and an encoded message, count the number of ways it can be decoded. For example, the message ‘111’ would give 3, since it could be decoded as ‘aaa’, ‘ka’, and ‘ak’. Y…...
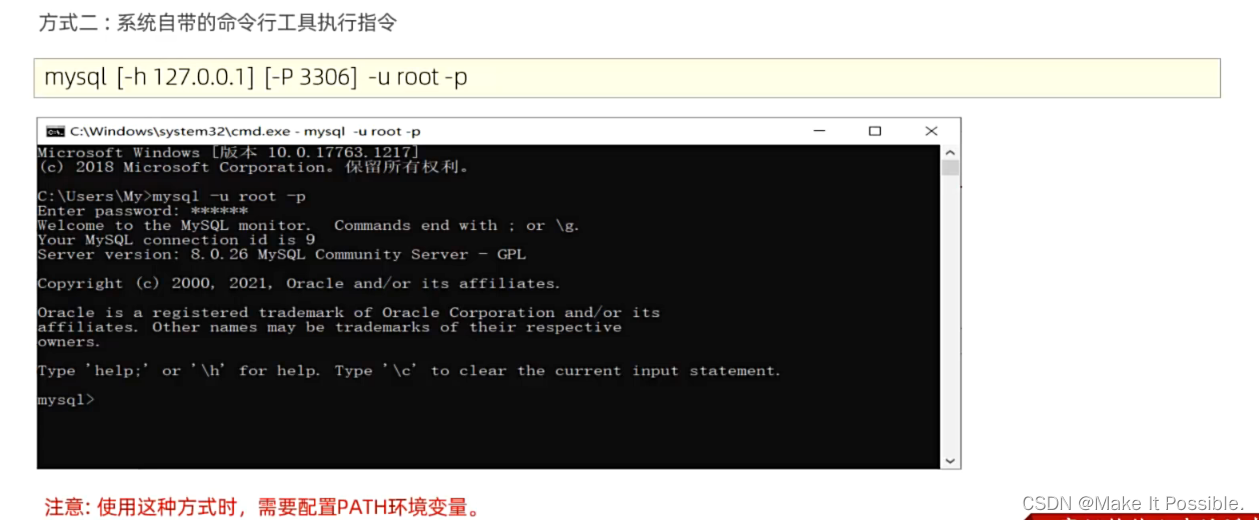
MySQ数据库: MySQL数据库的安装配置 ,图文步骤详细,一篇即可完成安装完成! MySQL数据库如何与客户端连接
LiuJinTao: 2024年4月14日 文章目录 MySQL的安装配置1. 下载2. 安装 三、 MySQL 启动与停止1. 第一种 方式:2. 第二种方式: 四、MySQL 客户端连接2. 方式二: MySQL的安装配置 1. 下载 官方下载网址:https://www.mysq…...

vue3+vant自动导入+pina+vite+js+pnpm搭建项目框架
vue3vant自动导入pinavitejspnpm搭建项目框架 文章目录 vue3vant自动导入pinavitejspnpm搭建项目框架1. 安装pnpm(如果还没有安装):2. 创建项目目录并进入该目录:3. 初始化项目:4. 安装Vite作为构建工具:5.…...
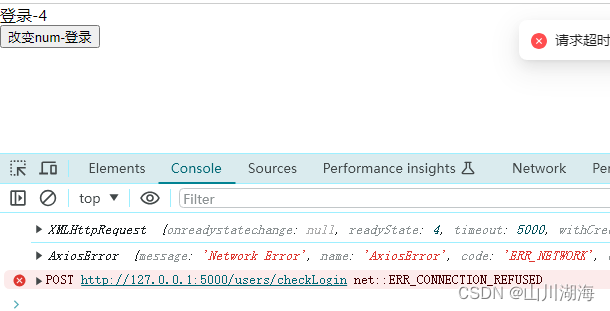
使用 Axios 处理 AxiosError 的三种常见方法
在使用 Axios 时处理 AxiosError 有几种常见的方法: 使用 try-catch 语句捕获异常: try {const response await axios.get(/api/data);// 处理响应数据 } catch (error) {if (error.response) {// 请求成功但状态码不在 2xx 范围console.log(error.response.data);console.l…...

linux上安装Tomcat
安装Tomcat 安装JDK https://www.oracle.com/java/technologies/downloads/#license-lightbox mkdir -p /usr/java tar xf jdk-11.0.22_linux-x64_bin.tar.gz ln -sv /usr/java/jdk /usr/java/jdk-11.0.22配置环境变量: cat > /etc/profile.d/java.sh <&…...
Ubuntu20.04安装ROS过程记录以及常见报错处理
官网安装步骤如下: http://wiki.ros.org/cn/noetic/Installation/Ubuntu#A.2BXwBZy1uJiMU- 第一个:添加ROS软件源 sudo sh -c echo "deb http://packages.ros.org/ros/ubuntu $(lsb_release -sc) main" > /etc/apt/sources.list.d/ros-la…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
