C++ 算法主题系列之集结0-1背包问题的所有求解方案
1. 前言
背包问题是类型问题,通过对这一类型问题的理解和掌握,从而可以归纳出求解此类问题的思路和模板。
背包问题的分类有:
0-1背包问题,也称为不可分割背包问题。- 无限背包问题。
- 判定性背包问题.
- 带附属关系的背包问题。
- 双背包求最优值.
- 构造三角形问题.
- 带上下界限制的背包问题(
012背包) - ……
本文将介绍0-1背包问题的各种求解方案,通过对各种求解方案的研究,从而全方面了解0-1背包问题的本质。
2. 0-1 背包问题
问题描述:
有一背包,能容纳的重量为 m,现有 n种物品,每种物品有重量和价值 2 个属性。请设计一个算法,在不分割物品的情况下,保证背包中所容纳的物品的总价值是最大的。
0-1背包也称为完全背包或不可分割背包问题,是一类常见的背包问题。常用的实现方案有递归和动态规划 。
2.1 递归算法
可以有 3 种写法。
2.1.1 第一种递归回溯方案
回顾递归回溯算法适合的问题域:
- 待解决的问题可以分多步。如迷宫问题、排列组合问题……
- 每一步都可能存在多个选择,当某一个选择行不通,或此选择结束后,可以回溯到上一步再另行选择。
那么背包问题是否适合上述的要求?
- 可以想象背包里有很多个格间。当每一个格间填充完毕,则表示得到一种求解。
- 对于格间而言,每一种物品都是一种选择,可以通地回溯再选择另一个物品。
- 其本质是对物品进行任意组合,然后再选择总价值最大的一种组合。
如下图,有 3 个物品需要放置入容量为 50 的背包中。初始可把背包想象成一个大格间,此时可以试着放入物品中的一个。
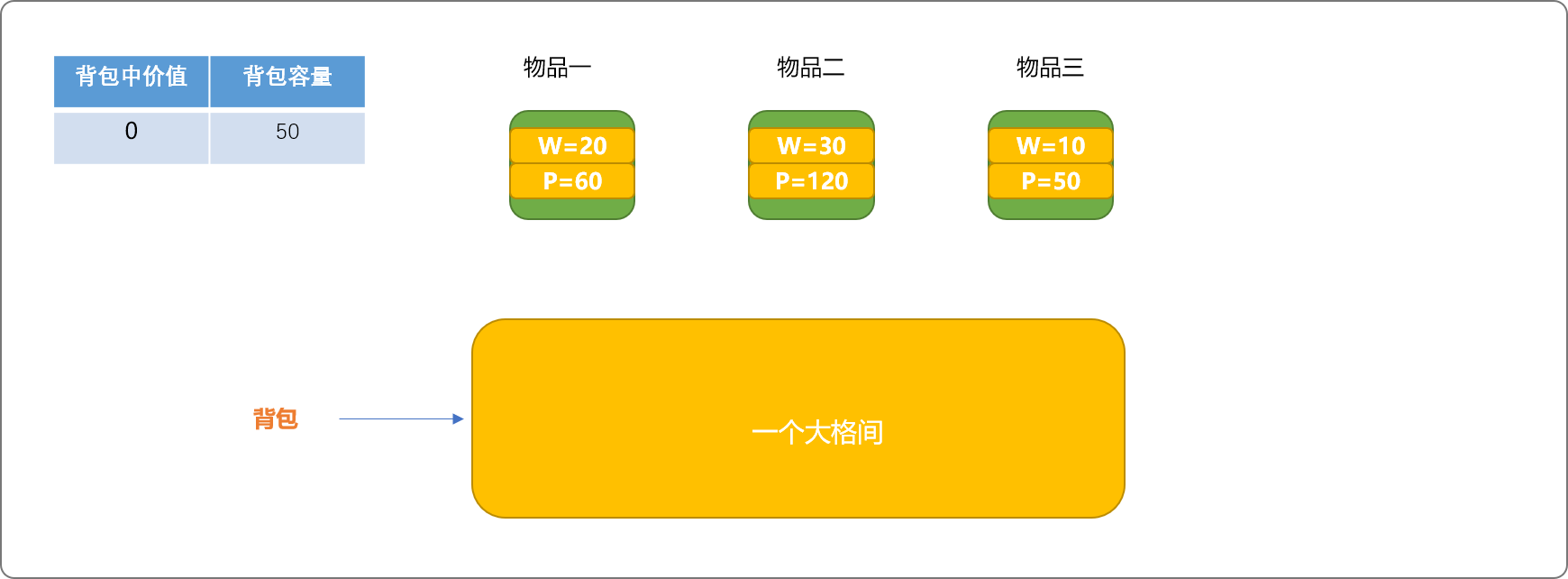
物品放入格间的条件:
- 物品不曾在背包中。
- 物品的重量小于或等于背包现有容量。
如下图,把物品一放入背包中。且把背包剩下空间想象为一个格间,在余下的物品中选择一个放入此格间中。
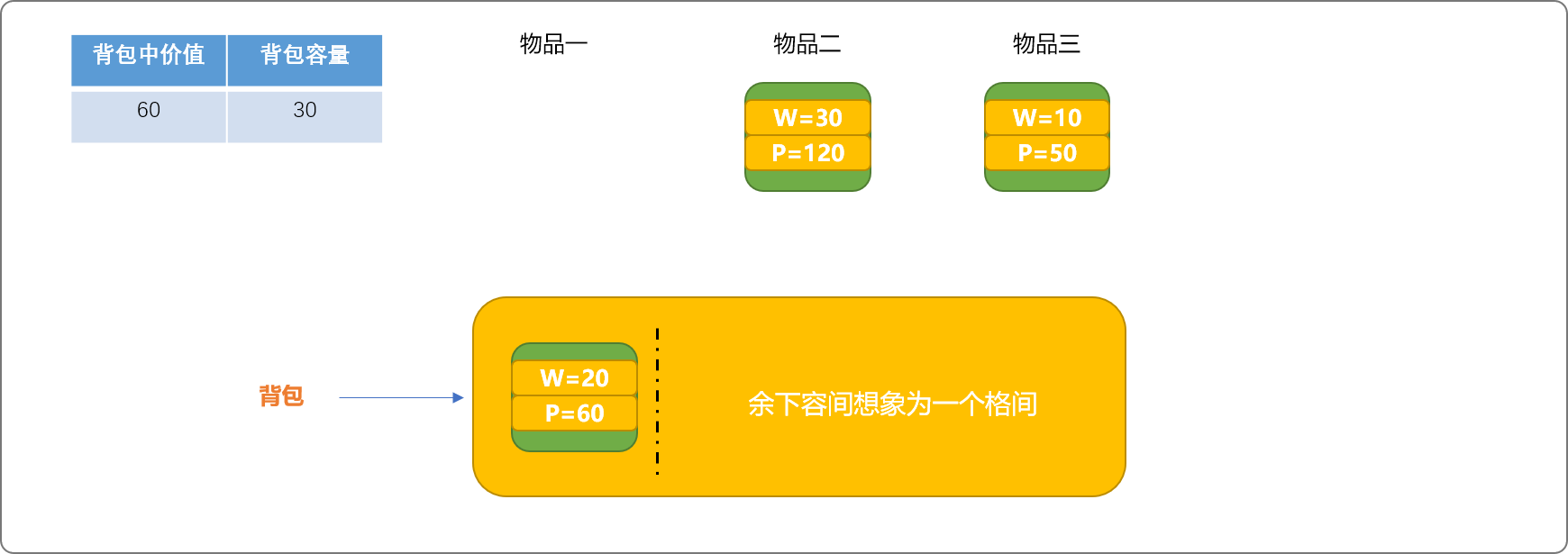
如下,把物品二放入格间中。
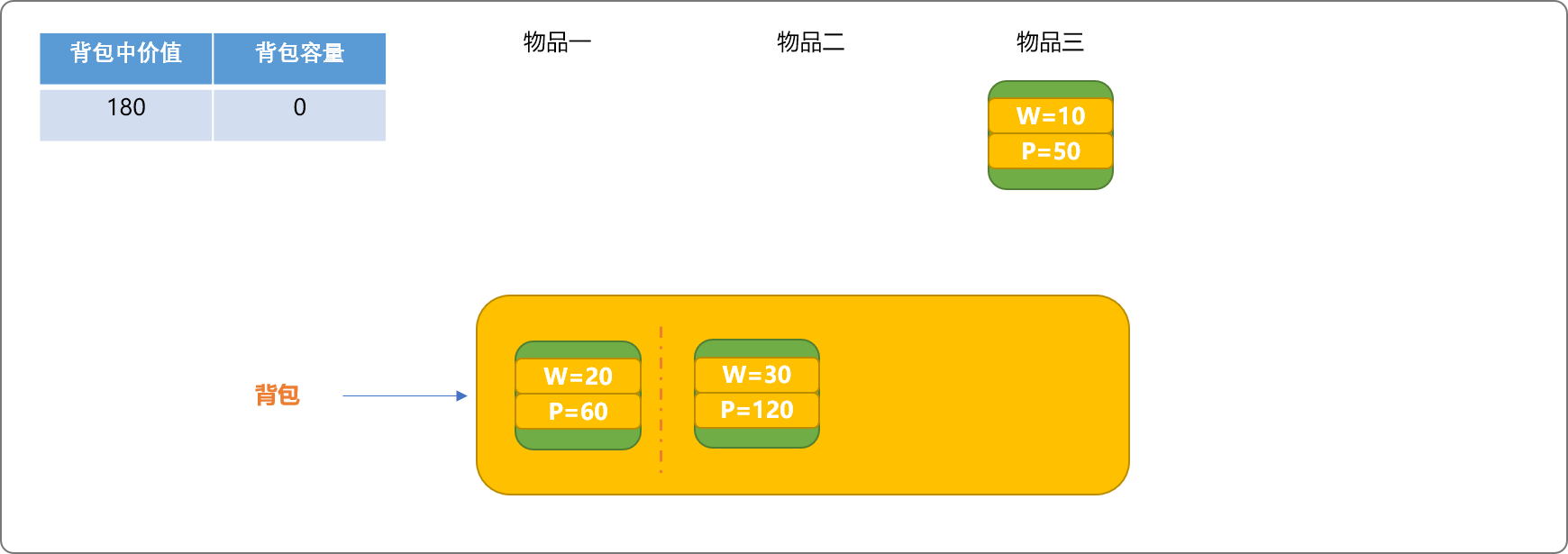
因物品一和物品二的重量之和为 50。等于背包总容量。此时,背包中已经没有剩余空间。也意味着不能再向此背包中放入物品。
至此,可以输出背包中的物品,且把背包中的总价值 180 存储在全局变量中,以便在后续操作时,查找是否还有比此值更大的值。
回溯物品
所谓回溯物品,指把物品从背包中移走,试着再放入一个其它物品。
如下图,回溯物品二,腾出格间。因物品三满足放入条件,放入格间。
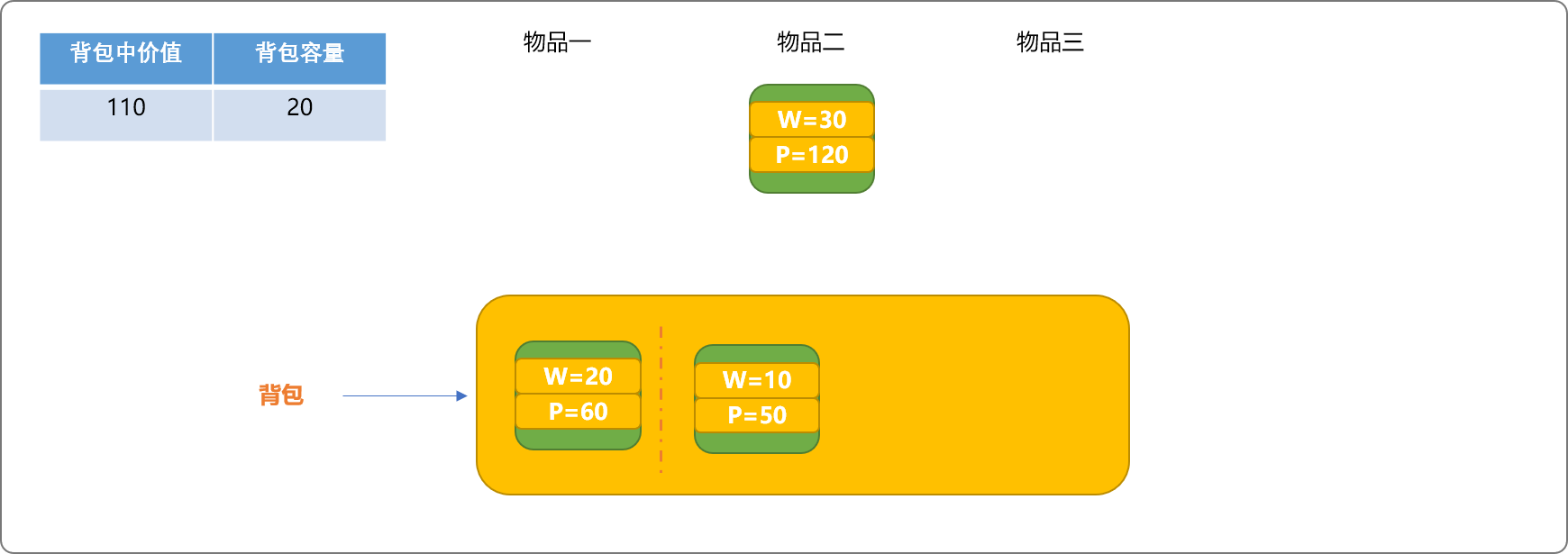
此时,背包还有剩余空间,同样把剩余空间想象成一个格间。因有剩余空间,可以试着把物品二放入背包中。
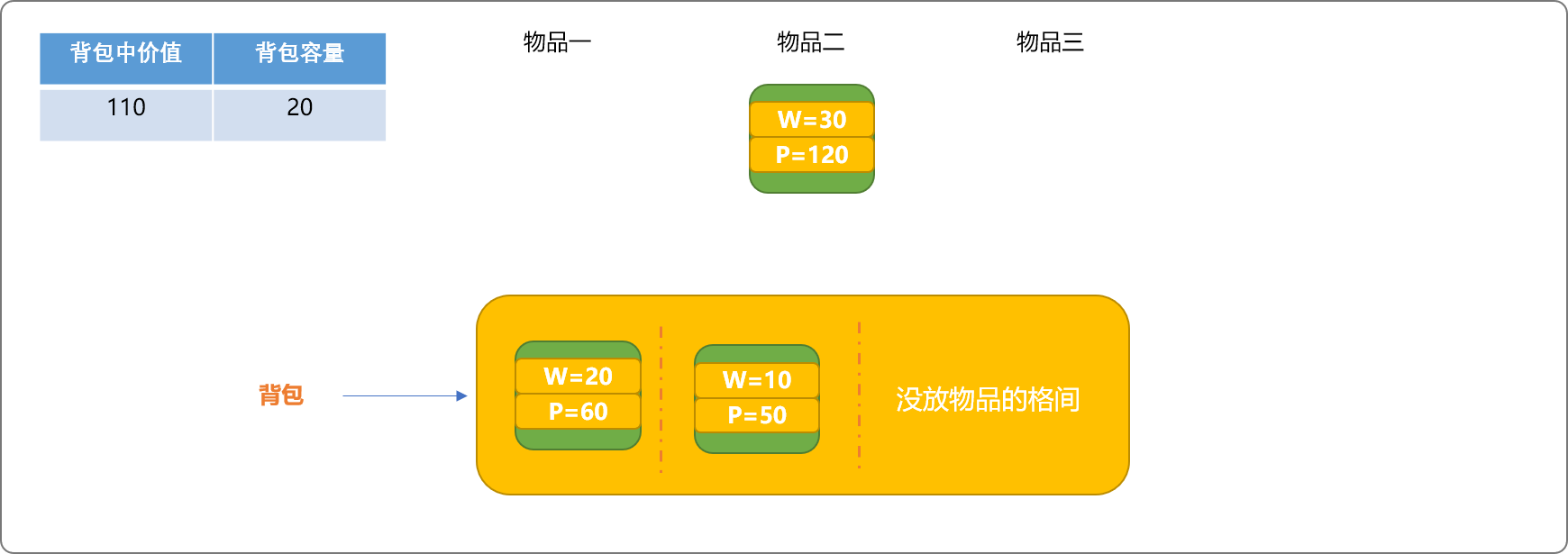
但因物品二的重量大于背包已有的容量,不能放入。此时,可以输出背包中的物品信息,并记录背包中的最大价值为110。因比前面的180的值小,继续保留 180这个价值为当前最大值。
对上述流程做一个简单总结:
-
当背包还有空间,且有物品可以放入时,则加入到背包中。
-
当背包不再能放下任何一件物品时,计算此时的总价值,并确定是不是最大价值。
Tips:这里有一点需要注意,递归函数的出口有
2个,一是还有物品可选择,但不能放入背包中。二是不再有物品可供选择。 -
回溯当前已经放入物品,选择其它物品,重复上述过程,一直到找到真正的最大值。
代码如下所示:
#include<bits/stdc++.h>
using namespace std;
struct Goods {//重量int weight;//价值int price;//装入状态bool isUse;
};
/*
*初始化
*/
Goods allGoods[3]= { {20,60,false},{30,120,false},{10,50,false}};//背包重量
int weight=50;
//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
/*
* 0-1 背包
* idx:物品编号,只需要考虑组合
* deep:递归深度
*/
void bag(int idx,int deep,int weight) {//每次都可以从所有物品中进行选择for(int i=idx; i<3; i++) {if( allGoods[i].isUse==false ) {//物品不曾放入背包if( allGoods[i].weight<=weight) {//且可以放下,增加背包中的总价值totalPrice+=allGoods[i].price;//标志此物品已经放入allGoods[i].isUse=true;//继续放置物品bag(i,deep+1,weight - allGoods[i].weight);//回溯totalPrice-=allGoods[i].price;allGoods[i].isUse=false;} else {//出口一:不可以放下,计算此时背包中的物品的价值是否是最大值,cout<<"-----------查询到某个物品不能放下时,显示背包中信息------------"<<endl;if(totalPrice>maxPrice) maxPrice= totalPrice;for(int j=0; j<3; j++)if(allGoods[j].isUse)cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;return ;}}}//出口二:不再有物品可以选择cout<<"--------当没有物品可选择时也要显示背包中物品信息-----------"<<endl;if(totalPrice>maxPrice) maxPrice= totalPrice;cout<<"此时背包中物品"<<endl;for(int j=0; j<3; j++)if(allGoods[j].isUse)cout<<allGoods[j].weight<<","<<allGoods[j].price<<endl;
}
//测试
int main() {bag(0,1,weight);cout<<"---------------------"<<endl;cout<<"最终背包中最大价值"<<maxPrice<<endl;return 0;
}
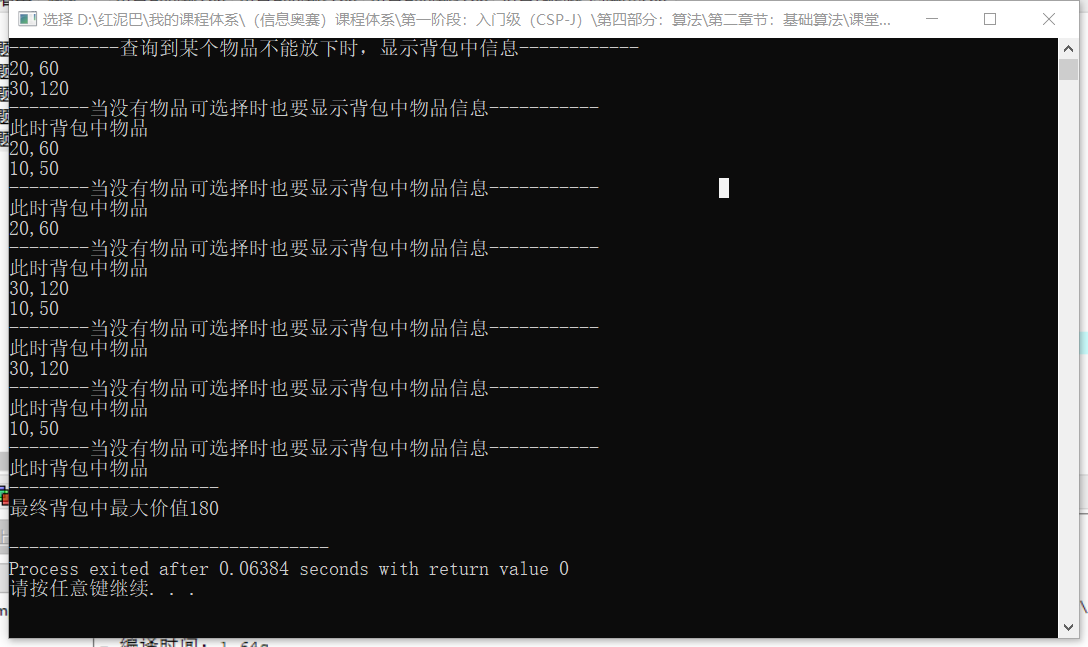
测试结果:
2.1.2 第二种回溯方案
第一种回溯方案,略显复杂,可以采用下面的回溯方案。
此方案中把物品可放入和不可放入做为选择。但其本质和上述实现是一样的。
#include<bits/stdc++.h>
using namespace std;
struct Goods {//物品重量int weight;//物品价值int value;//物品状态 1 已经使用,0 未使用int isUse;
};//最大价值
int maxPrice=0;
//总价值
int totalPrice=0;
//背包重量
int bagWeight=100;
//物品信息
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
int count=4;
/*
*显示背包中物品
*/
void showBag() {for(int i=0; i<5; i++) {if(allGoods[i].isUse)cout<<allGoods[i].weight<<","<<allGoods[i].value<<endl;}
}
/*
* idx: 物品编号
* count: 物品总数量
*/
void zeroAndOneBag(int idx,int weight) {//物品只有两种状态for(int i=0; i<=1; i++) {if( weight-allGoods[idx].weight*i>=0 ) {//物品状态allGoods[idx].isUse=i;//总价值totalPrice+=allGoods[idx].value*i;if(idx==4) {if(totalPrice>maxPrice) {maxPrice=totalPrice;cout<<"------------"<<endl;showBag();cout<<maxPrice<<endl;}} else {zeroAndOneBag(idx+1,weight-allGoods[idx].weight*i);}//回溯allGoods[idx].isUse=0;totalPrice-=allGoods[idx].value*i;}}
}
//测试
int main() {zeroAndOneBag(0,bagWeight);return 0;
}
2.1.3 第三种方案
前两种方案,不仅可得到最优值,且可以得到寻找过程中的各种组合方案。如果仅仅是想得到最终结果,不在乎中间的过程,则可以使用下面的递归方案。
#include<iostream>
#include<windows.h>//max函数
using namespace std;
struct Goods {//重量int weight;//价值int price;//装入状态bool isUse;
};
//所有物品
Goods allGoods[5]= { {20,60,false},{30,120,false},{10,50,false},{20,20,false},{40,100,false} };
//背包重量
int bagWeight = 100;
//物品总数量
int totalNumber = 5;
/*
*递归
*/
int zeroAndOneBag(int index, int remainWeight) {int totalPrice = 0;//没有物品可放if (index == totalNumber) return 0;if (allGoods[index].weight > remainWeight)//当前物品不能放入,查看其它物品放入的情况totalPrice = zeroAndOneBag(index + 1, remainWeight);else//当前物品可以放入,则在把此物品放入和不放入背包时的最大价值 totalPrice = max(zeroAndOneBag(index + 1, remainWeight -allGoods[index].weight) + allGoods[index].price, zeroAndOneBag(index + 1, remainWeight));return totalPrice;
}
//测试
int main() {int value = zeroAndOneBag(0, bagWeight);cout << value << endl;return 0;
}
2.2 动态规划
背包问题,有 2 个状态值,背包的容量和可选择的物品。
- 物品对于背包而言,只有
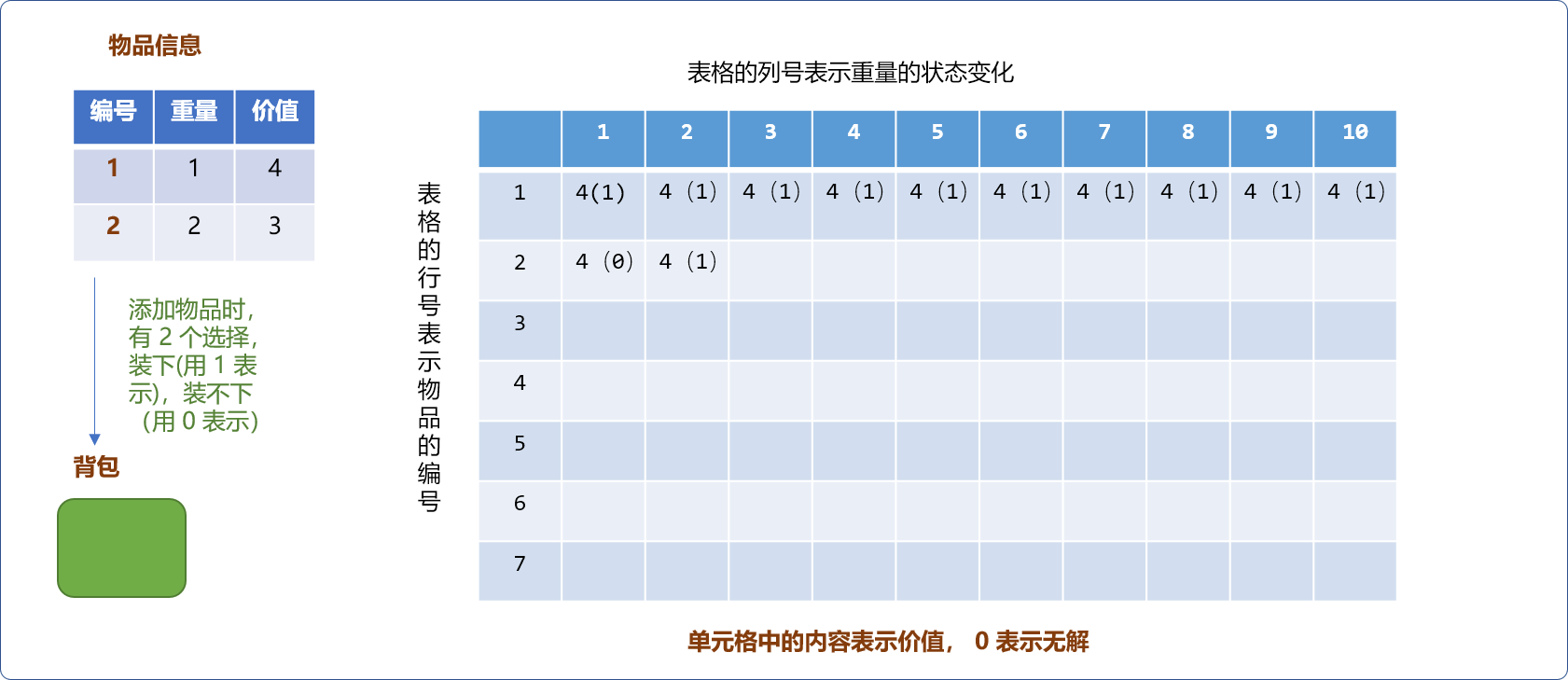
2种选择,要么装下物品,要么装不下,如下图所示,表格的行号表示物品编号,列号表示背包的重量。单元格中的数字表示背包中最大价值。当物品只有一件时,当物品重量大于背包容量,不能装下,反之,能装下。如下图,物品重量为1。无论何种规格容量的背包都能装下(假设背包的容量至少为1)。
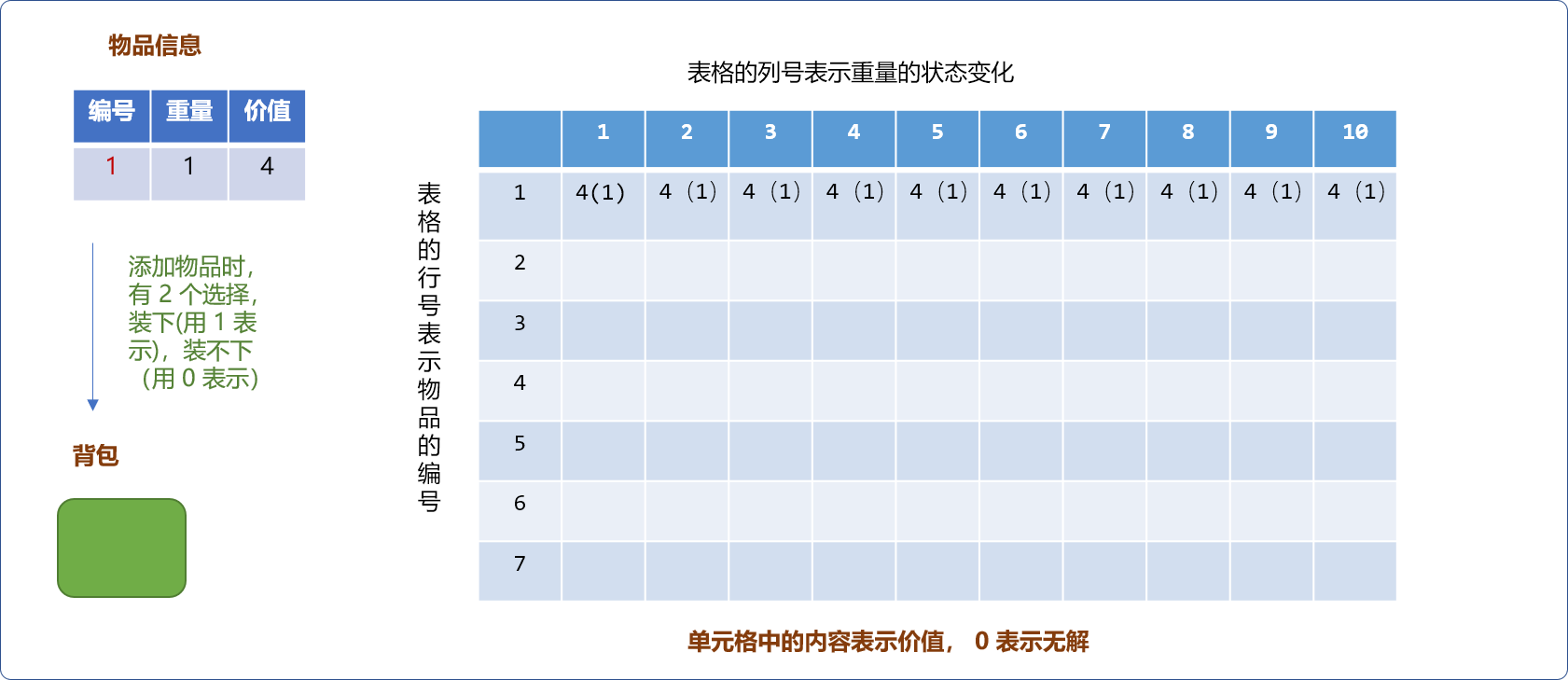
- 如下图,当增加重量为
2的物品后,当背包的容量为1时,不能装下物品,则最大值为同容量背包中已经有的最大值。
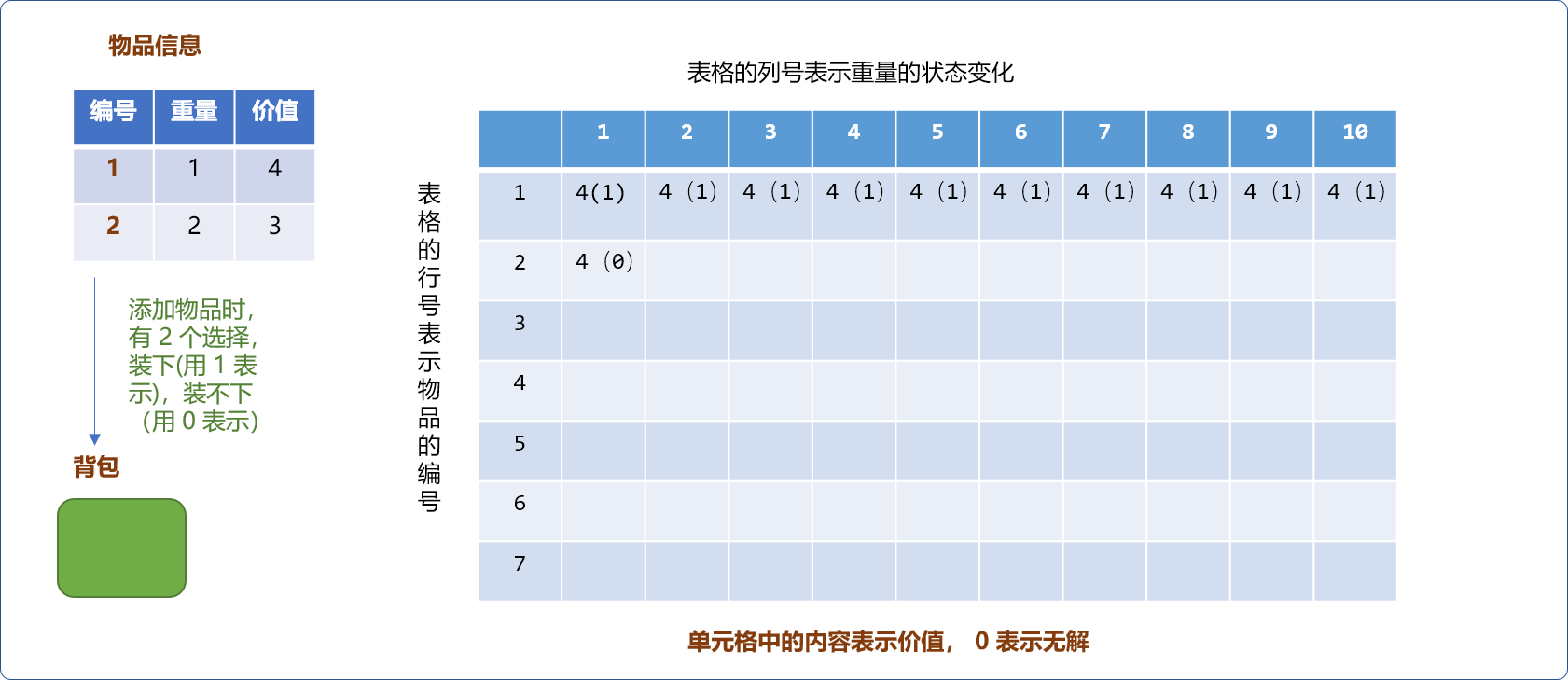
但对容量为 2的背包而言,恰好可以放入新物品,此时背包中的最大价值就会有 2 个选择,一是把物品 2 放进去,背包中的价值为 3。二是保留背包已有的价值4。然后,在两者中选择最大值 4。
当背包容量是 3时,物品2也是可以放进去的。此时背包的价值可以是当前物品的价值 3加上背包剩余容量3-2=1能存放的最大价值4,计算后值为 7。要把此值和不把物品放进去时原来的价值 4 之间进行最大值选择。
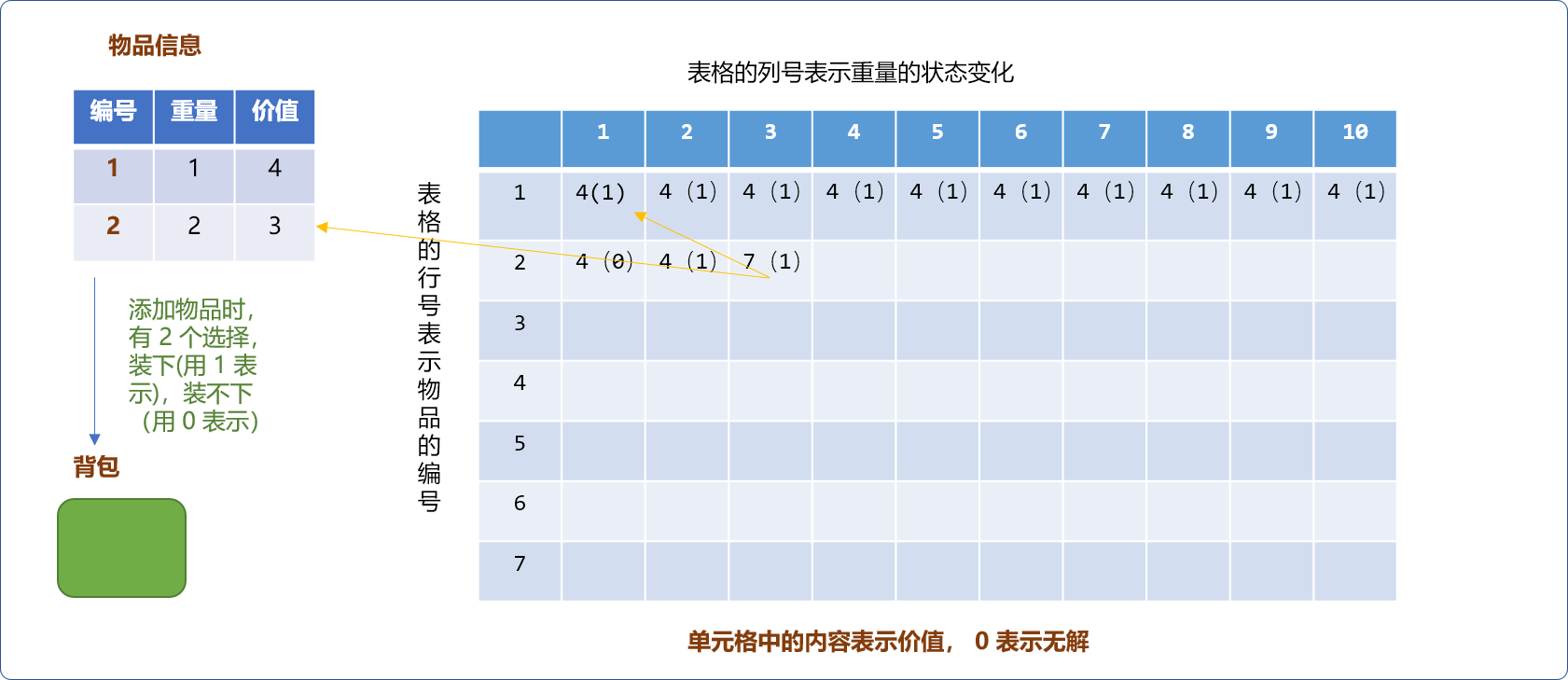
所以,对于背包问题,核心思想就是:
- 如果物品能放进背包:则先计算出物品的价值加上剩余容量能存储的最大价值之和,再找到不把物品放进背包时背包中原有价值。最后在两者之间进行最大值选择。
- 当物品不能放进背包:显然,保留背包中原来的最大价值信息。
2.3.3 编码实现
#include <iostream>
#include <vector>
using namespace std;
int main(int argc, char** argv) {//物品信息int goods[3][3]= { {1,4},{2,3} };//背包容量int bagWeight=0;cout<<"请输入背包容量:"<<endl;cin>>bagWeight;//状态表int db[4][bagWeight+1]= {0};for(int i=0; i<4; i++) {for(int j=0; j<bagWeight+1; j++) {db[i][j]=0;}}for(int w=1; w<4; w++) {for(int wt=1; wt<=bagWeight; wt++) {if( goods[w-1][0]>wt ) {//如果背包不能装下物品,保留背包上一次的结果db[w][wt]=db[w-1][wt];} else {//能装下,计算本物品价值和剩余容量的最大价值int val=goods[w-1][1] + db[w-1][ wt- goods[w-1][0] ];//背包原来的价值int val_= db[w-1][wt];//计算最大值db[w][wt]=val>val_?val:val_;}}}for(int i=1; i<3; i++) {for(int j=1; j<=bagWeight; j++) {cout<<db[i][j]<<"\t";}cout<<endl;}return 0;
}
输出结果:
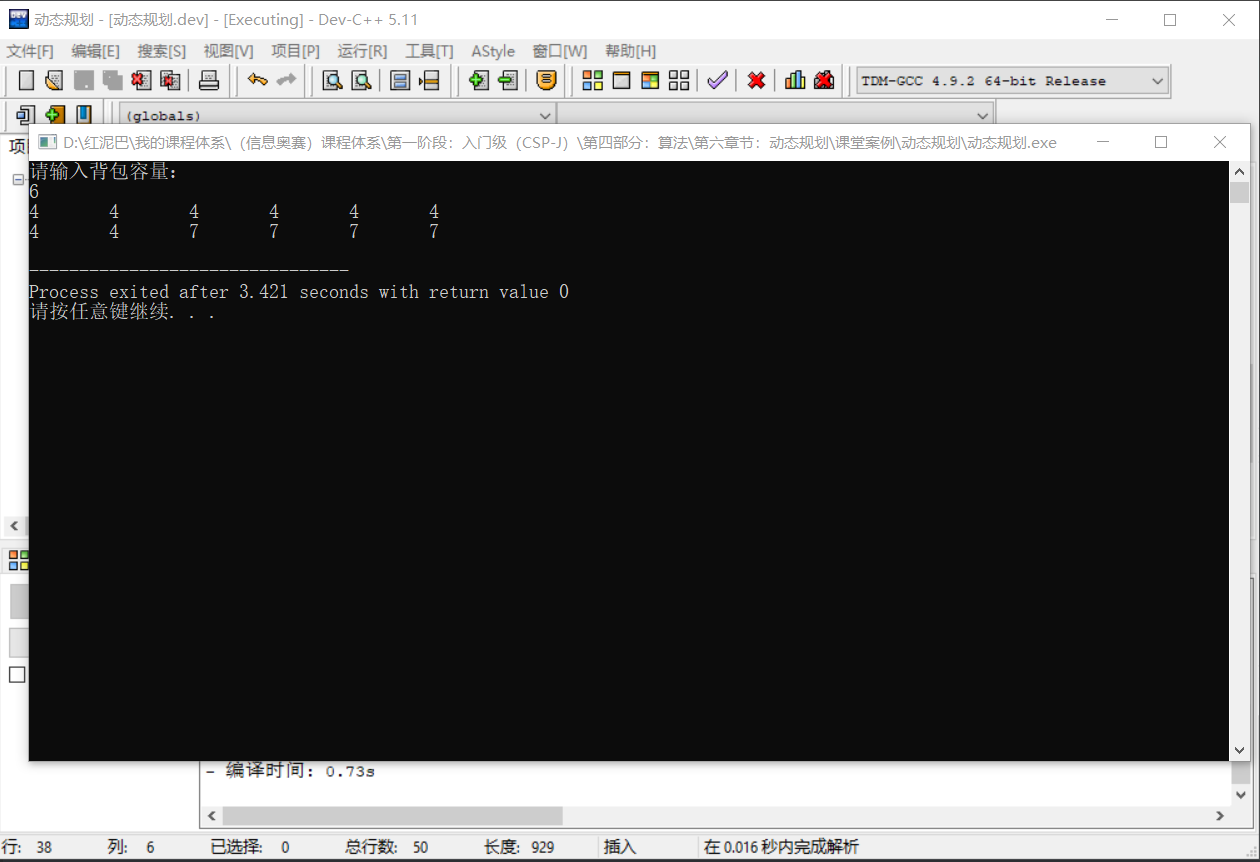
3. 总结
本文主要讲解背包系列 中的0-1背包问题。0-1背包问题可以使用递归和动态规划方案得到其解。
相关文章:

C++ 算法主题系列之集结0-1背包问题的所有求解方案
1. 前言 背包问题是类型问题,通过对这一类型问题的理解和掌握,从而可以归纳出求解此类问题的思路和模板。 背包问题的分类有: 0-1背包问题,也称为不可分割背包问题。无限背包问题。判定性背包问题.带附属关系的背包问题。双背包…...

【Vue】Vue常见的6种指令
Vue的6种指令-前言指令(Directives)是vue 为开发者提供的模板语法,用于辅助开发者渲染页面的基本结构。vue 中的指令按照不同的用途可以分为如下6 大类① 内容渲染指令 ② 属性绑定指令 ③ 事件绑定指令 ④ 双向绑定指令 ⑤ 条件渲染指令 ⑥ …...
四年学习资料_文件目录树)
计算机科学与技术(嵌入式)四年学习资料_文件目录树
说明: 资料内容主要包括:计嵌专业2019级大学四年主要科目的各种电子资料,有电子实验报告、课程设计报告、课程设计项目、整理复习笔记、电子书、ppt、练习题、期末试卷、部分课程软件资源、科创项目,职业生涯规划书,大…...
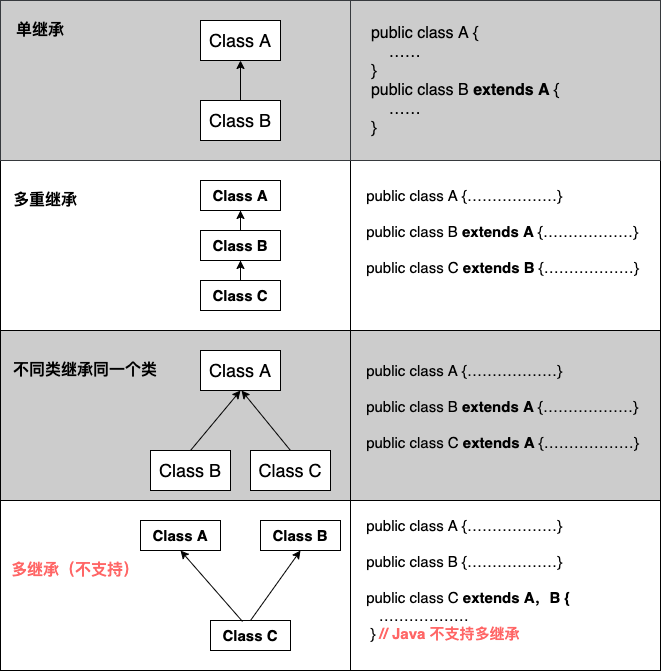
【java】Java 继承
文章目录继承的概念生活中的继承:类的继承格式为什么需要继承公共父类:继承类型继承的特性继承关键字extends关键字implements关键字super 与 this 关键字final 关键字构造器继承的概念 继承是java面向对象编程技术的一块基石,因为它允许创建…...

自媒体账号数据分析从何入手?
账号的数据可以直接反应这个账号的好坏,数据越高收益就会越好,数据越差收益自然高不了。 新手要从哪些方面入手见效更快呢?今天大周就来把自己的经验分享给粉丝们! 1、账号定位 (1)账号所创作的领域 &a…...

Clickhouse新版本JSON字段数据写入方式
Clickhouse新版本JSON字段数据写入方式 在Clickhouse版本22.3.1版本以上,提供了针对JSON格式数据的新的数据类型:JSON,从而实现了存储此类数据由原先的结构化表结构,更新为现在的半结构化表存储。对于新增字段,某些同…...

HNU-电路与电子学-实验2
实验二 模型机组合部件的实现(一) 班级 计XXXXX 姓名 wolf 学号 2021080XXXXX 一、实验目的 1.了解简易模型机的内部结构和工作原理。 2.熟悉译码器、运算器的工作原理。 3.分析模型机的功…...
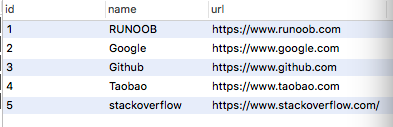
从0开始学python -49
Python MySQL - mysql-connector 驱动 -2 插入数据 插入数据使用 “INSERT INTO” 语句: demo_mysql_test.py: 向 sites 表插入一条记录。 import mysql.connectormydb mysql.connector.connect(host"localhost",user"root",passwd"…...

Spring MVC 详解(连接、获取参数、返回数据)
在之前我们先简单那谈谈Spring、SpringBoot以及Spring MVC框架之间有什么关系?首先Spring是一个框架,SpringBoot脚手架是为了快速开发Spring框架而创造的技术。可以理解为SpringBoot又在Spring上面包了一层壳子,是基于Spring的,是…...
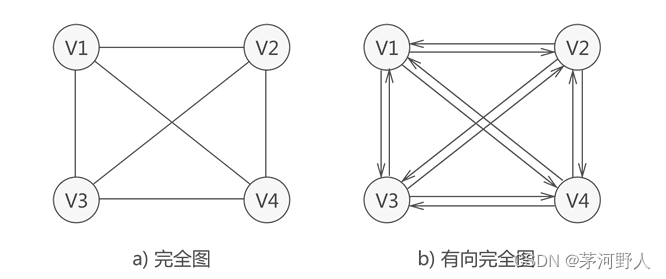
IT女神节(致敬中国IT界永远的女神严蔚敏-数据结构)
我们都知道程序数据结构算法。相信很多人都学过严蔚敏的数据结构的课程。作为一个码农,在这不管是3.7女神节,还是3.8妇女节。我觉得都有必要向这些教育界的老前辈致敬。今天我就梳理梳理,最经典的数据结构教材。 严蔚敏介绍(来自…...

Java 集合分页
一、前言 在Java开发中,若单次展示的数据量太大,会造成程序响应缓慢,就需要用到 分页 功能,每一页展示一定量的数据,分多次展示 ... 那么在List集合中,如何实现 分页 功能呢? 本文将以3种方式&a…...

代码随想录之哈希表(力扣题号)
242. 有效的字母异位词 直接用数组模拟哈希表 只有小写字母,开26的数组就可以了 class Solution {public boolean isAnagram(String s, String t) {//24-28int[] hash new int[26];Arrays.fill(hash,0);for(int i0;i<s.length();i){hash[s.charAt(i)-a];}for(i…...
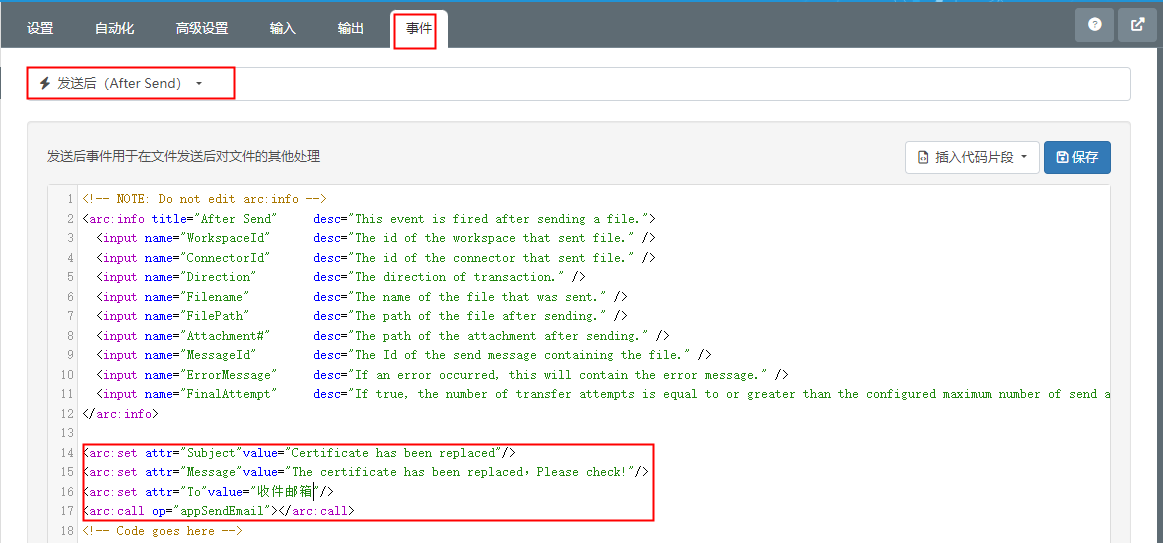
如何在知行之桥EDI系统中定时自动更换交易伙伴AS2证书?
为了保证客户与交易伙伴之间数据传输的安全性,AS2传输协议中,通常会通过一对数字证书对传输数据进行签名和加密。但是证书是有有效期的,在证书到期之前,需要贸易双方及时更换新的证书。 在更新证书时,由于客户通常是和…...

辽宁千圣文化:抖音店铺怎么做二次优化?
抖音商品卡订单是指永华在抖音、抖音极速版,通过直播的方式出现短视频页面商品卡之后,直接成交商品详情页直接成交后的订单,那么跟着辽宁千圣文化小编来一起看看吧!一.与政策有关1.什么是「商品卡订单」?用户通过抖音、…...

检测js代码中可能导致内存泄漏的工具
JavaScript 中闭包等问题可能导致内存泄漏,因为闭包中引用的变量不会被垃圾回收器自动释放。以下是一些可以用来检测 JavaScript 代码中可能导致内存泄漏的工具: 1、Chrome 开发者工具 Chrome 开发者工具中有一个 Heap Profiler 工具,可以帮…...

linux和centos读写日期到文件并对日期进行比较
#!/bin/bash adate -d "${a}" %s #必须用数字 %s是取时间戳秒数 ddate -d "${c}" %s echo m$(($a - $d)) #必须2个小括号 a1date %s echo $a1 sleep 2 b1date %s echo $(($a1 - $b1)) #必须2个小括号 if [ $a1 -eq $b1 ];then #必须有空格 echo "…...

Espressif-IDE v2.8.0 新增功能及开发方向
在乐鑫最近发布的 Espressif-IDE 2.8.0 版本中,我们推出了分区表编辑器和 NVS 分区编辑器功能,优化现有调试器的配置功能并修复多项 Bug ,进一步为用户提升了插件质量以及稳定性。 用户可以点此获取最新版本。 • 若您的设备为 Windows 系统…...

C++学习笔记之基础
目录前言一.零碎知识点二.C核心2.1.内存分区2.2.引用2.3.函数2.4.类和对象2.4.1.对象的初始化和清理2.4.2.构造函数和析构函数2.4.3.构造函数的分类和调用2.4.4.拷贝构造函数的调用时机2.4.5.深拷贝与浅拷贝2.4.6.初始化列表2.4.7.类对象作为类的成员2.4.8.静态成员2.4.9.C对象…...
)
博弈论小课堂:零和博弈(找到双方的平衡点)
文章目录 引言I 零和博弈1.1 零和博弈的策略1.2 博弈类型1.3 找到平衡点(equilibrium)II 多人博弈的投篮问题2.1 比赛规则2.2 零和博弈的计算引言 从概率论延伸出来的课题——博弈论,博弈论中最典型的两大类博弈,是“零和博弈”与“非零和博弈”。博弈论所研究的最优化问题…...
)
Redisson 分布式锁(基于v1.3.1)
Redisson 分布式锁 v1.0.0版本问题 v1.0.0版本的实现在持有锁的JVM或者持有锁的线程挂掉没有释放锁时,该锁不会被释放并且会一直占用,这个时候就使用DEL命令手动删除。 问题解决 v1.3.1版本通过key的ttl解决了这个问题,关键加锁逻辑改为了…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

【Qt】控件 QWidget
控件 QWidget 一. 控件概述二. QWidget 的核心属性可用状态:enabled几何:geometrywindows frame 窗口框架的影响 窗口标题:windowTitle窗口图标:windowIconqrc 机制 窗口不透明度:windowOpacity光标:cursor…...

从数据报表到决策大脑:AI重构电商决策链条
在传统电商运营中,决策链条往往止步于“数据报表层”:BI工具整合历史数据,生成滞后一周甚至更久的销售分析,运营团队凭经验预判需求。当爆款突然断货、促销库存积压时,企业才惊觉标准化BI的决策时差正成为增长瓶颈。 一…...
