acwing算法提高之图论--最近公共祖先
目录
- 1 介绍
- 2 训练
1 介绍
本博客用来记录"对于有根图中,求最近公共祖先"的题目。
求解方法:
- 向上标记法。每次求两个结点的最近公共祖先的时间复杂度是
O(N)。由于时间复杂度较高,通常不用。 - 倍增法。
倍增法重要思路:预处理出两个数组fa[i][j]和depth[i]。其中fa[i][j]表示从i开始,向上走2^j步所能走到的结点。0<=j<=logn。depth[i]表示深度,为到根结点的距离再加上1。
哨兵:如果从i开始跳2^j步会跳过根结点,那么fa[i][j] = 0,depth[0] = 0。
倍增法重要步骤:
- 先将两个点跳到同一层。
- 让两个点同时往上跳,一直跳到它们的最近公共祖先的下一层。
倍增法的时间复杂度分析:预处理的时间复杂度为O(NlogN),查询的时间复杂度为O(logN)。
2 训练
题目1:1172祖孙询问
C++代码如下,
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>using namespace std;const int N = 40010;
int n, m;
int depth[N], fa[N][16];
int ancestor;
unordered_map<int, vector<int>> g;void bfs(int root) {memset(depth, 0x3f, sizeof depth);depth[0] = 0;depth[root] = 1; queue<int> q;q.push(root);while (!q.empty()) {int a = q.front();q.pop();for (auto b : g[a]) {if (depth[b] > depth[a] + 1) {depth[b] = depth[a] + 1;q.push(b);fa[b][0] = a;for (int k = 1; k <= 15; ++k) {fa[b][k] = fa[fa[b][k-1]][k-1];}}}}return;
}int lca(int a, int b) {//倍增法if (depth[a] < depth[b]) swap(a, b);for (int k = 15; k >= 0; --k) {if (depth[fa[a][k]] >= depth[b]) {a = fa[a][k];}}if (a == b) return a;for (int k = 15; k >= 0; --k) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];
}int main() {cin >> n;int a, b;for (int i = 0; i < n; ++i) {cin >> a >> b;if (b == -1) {ancestor = a;} else {g[a].emplace_back(b);g[b].emplace_back(a); }}cin >> m;vector<pair<int,int>> queries;for (int i = 0; i < m; ++i) {cin >> a >> b;queries.emplace_back(a,b);}//从根结点开始遍历bfs(ancestor);for (auto [a, b] : queries) {int x = lca(a, b);if (a == x) {puts("1");} else if (b == x) {puts("2");} else {puts("0");}}return 0;
}
题目2:1171距离
C++代码如下,
相关文章:

acwing算法提高之图论--最近公共祖先
目录 1 介绍2 训练 1 介绍 本博客用来记录"对于有根图中,求最近公共祖先"的题目。 求解方法: 向上标记法。每次求两个结点的最近公共祖先的时间复杂度是O(N)。由于时间复杂度较高,通常不用。倍增法。 倍增法重要思路࿱…...

C语言 函数——断言与防御式编程
目录 如何确定假设的真假? 断言 防御式编程(Defensive programming) 如何确定假设的真假? 程序中的假设 *某个特定点的某个表达式的值一定为真 *某个特定点的某个表达式的值一定位于某个区间等 问题:如何确定这些…...

【opencv】示例-travelsalesman.cpp 使用模拟退火算法求解旅行商问题
// 载入 OpenCV 的核心头文件 #include <opencv2/core.hpp> // 载入 OpenCV 的图像处理头文件 #include <opencv2/imgproc.hpp> // 载入 OpenCV 的高层GUI(图形用户界面)头文件 #include <opencv2/highgui.hpp> // 载入 OpenCV 的机器学习模块头文件 #includ…...

【linux深入剖析】深入理解软硬链接 | 动静态库的制作以及使用
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1.理解软硬链接1.1 操作观…...

xss常用标签和触发事件
无过滤情况 <script> <scirpt>alert("xss");</script> <img> 图片加载错误时触发 <img src"x" οnerrοralert(1)> <img src"1" οnerrοreval("alert(xss)")> 鼠标指针移动到元素时触发 <im…...

WPF中Binding的原理和应用
WPF中Binding的原理和应用 在WPF中,Binding机制是实现数据与界面的连接和同步的重要工具。了解Binding的原理和应用,对于开发人员来说是非常重要的。本文将详细介绍WPF中Binding的原理和应用,帮助读者更好地理解和运用这一强大的机制。 Bin…...

探索设计模式的魅力:深度挖掘响应式模式的潜力,从而精准优化AI与机器学习项目的运行效能,引领技术革新潮流
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,坚持默默的做事。 挖掘响应式模式,优化AI与机器学习项目性能,引领技术新潮流 ✨机器学习界的…...

《经典论文阅读2》基于随机游走的节点表示学习—Deepwalk算法
word2vec使用语言天生具备序列这一特性训练得到词语的向量表示。而在图结构上,则存在无法序列的难题,因为图结构它不具备序列特性,就无法得到图节点的表示。deepwalk 的作者提出:可以使用在图上随机游走的方式得到一串序列&#x…...

Java实现二叉树(下)
1.前言 http://t.csdnimg.cn/lO4S7 在前文我们已经简单的讲解了二叉树的基本概念,本文将讲解具体的实现 2.基本功能的实现 2.1获取树中节点个数 public int size(TreeNode root){if(rootnull){return 0;}int retsize(root.left)size(root.right)1;return ret;}p…...

Hello 算法10:搜索
https://www.hello-algo.com/chapter_searching/binary_search/ 二分查找法 给定一个长度为 n的数组 nums ,元素按从小到大的顺序排列,数组不包含重复元素。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素,则返回 -1 。 # 首…...

常见分类算法详解
在机器学习和数据科学的广阔领域中,分类算法是至关重要的一环。它广泛应用于各种场景,如垃圾邮件检测、图像识别、情感分析等。本文将深入剖析几种常见的分类算法,帮助读者理解其原理、优缺点以及应用场景。 一、K近邻算法(K-Nea…...

推送恶意软件的恶意 PowerShell 脚本看起来是人工智能编写的
威胁行为者正在使用 PowerShell 脚本,该脚本可能是在 OpenAI 的 ChatGPT、Google 的 Gemini 或 Microsoft 的 CoPilot 等人工智能系统的帮助下创建的。 攻击者在 3 月份的一次电子邮件活动中使用了该脚本,该活动针对德国的数十个组织来传播 Rhadamanthy…...

微服务之Consul 注册中心介绍以及搭建
一、微服务概述 1.1单体架构 单体架构(monolithic structure):顾名思义,整个项目中所有功能模块都在一个工程中开发;项目部署时需要对所有模块一起编译、打包;项目的架构设计、开发模式都非常简单。 当项…...

MES生产管理系统:私有云、公有云与本地化部署的比较分析
随着信息技术的迅猛发展,云计算作为一种新兴的技术服务模式,已经深入渗透到企业的日常运营中。在众多部署方式中,私有云、公有云和本地化部署是三种最为常见的选择。它们各自具有独特的特点和适用场景,并在不同程度上影响着企业的…...

【core analyzer】core analyzer的介绍和安装详情
目录 🌞1. core和core analyzer的基本概念 🌼1.1 coredump文件 🌼1.2 core analyzer 🌞2. core analyzer的安装详细过程 🌼2.1 方式一 简单但不推荐 🌼2.2 方式二 推荐 🌻2.2.1 安装遇到…...

个人练习之-jenkins
虚拟机环境搭建(买不起服务器 like me) 重点: 0 虚拟机防火墙关闭 systemctl stop firewalld.service systemctl disable firewalld.service 1 (centos7.6)网络配置 (vmware 编辑 -> 虚拟网络编辑器 -> 选择NAT模式 ->NAT设置查看网关) vim /etc/sysconfig/network-sc…...
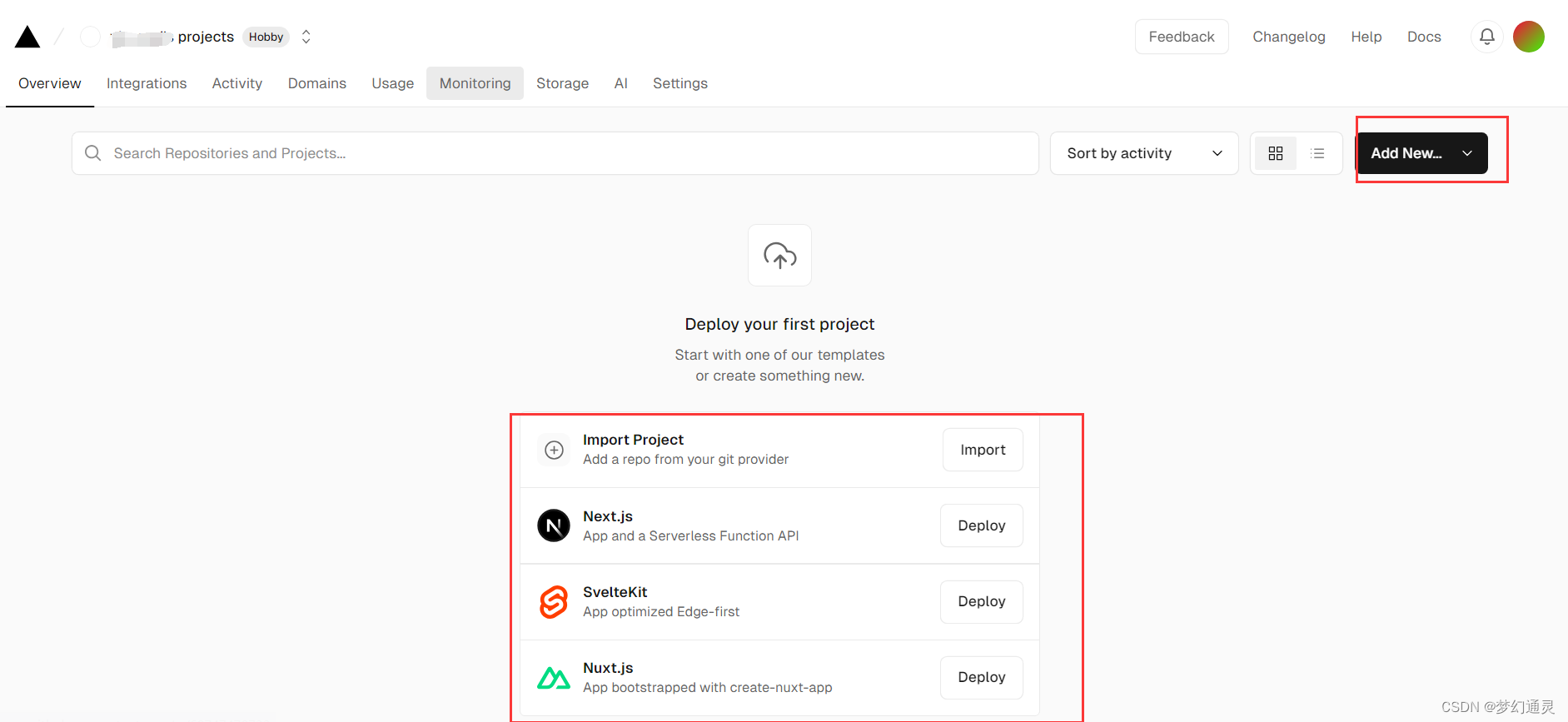
初探vercel托管项目
文章目录 第一步、注册与登录第二步、本地部署 在个人网站部署的助手vercel,支持 Github部署,只需简单操作,即可发布,方便快捷! 第一步、注册与登录 进入vercel【官网】,在右上角 login on,可登…...
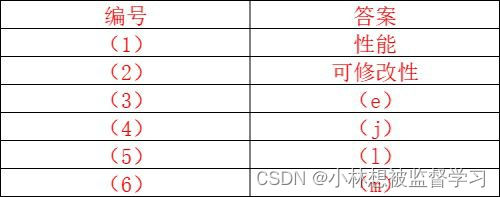
软考 - 系统架构设计师 - 质量属性例题 (2)
问题1: 、 问题 2: 系统架构风险:指架构设计中 ,潜在的,存在问题的架构决策所带来的隐患。 敏感点:指为了实现某个质量属性,一个或多个构件所具有的特性 权衡点:指影响多个质量属性…...

基于Python豆瓣电影数据可视化分析系统的设计与实现
大数据可视化项目——基于Python豆瓣电影数据可视化分析系统的设计与实现 2024最新项目 项目介绍 本项目旨在通过对豆瓣电影数据进行综合分析与可视化展示,构建一个基于Python的大数据可视化系统。通过数据爬取收集、清洗、分析豆瓣电影数据,我们提供了…...
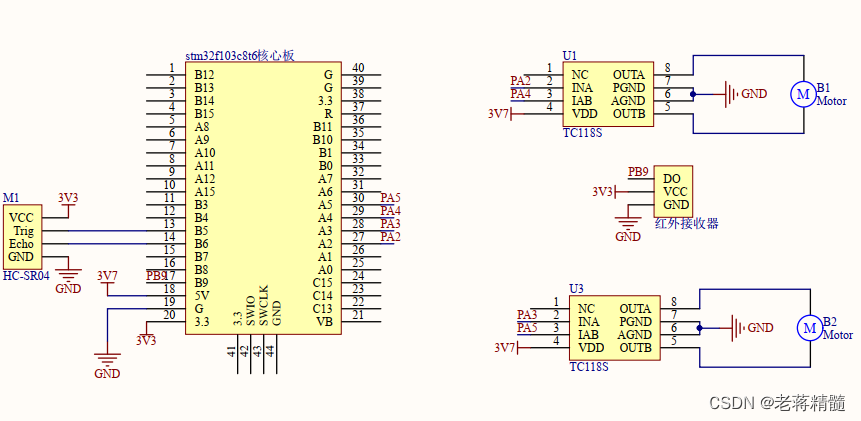
【已开源】基于stm32f103的爬墙小车
基于stm32f103的遥控器无线控制爬墙小车,实现功能为可平衡在竖直墙面上,并进行移动和转向,具有超声波防撞功能。 直接上: 演示视频如:哔哩哔哩】 https://b23.tv/BzVTymO 项目说明: 在这个项目中&…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...

【2D与3D SLAM中的扫描匹配算法全面解析】
引言 扫描匹配(Scan Matching)是同步定位与地图构建(SLAM)系统中的核心组件,它通过对齐连续的传感器观测数据来估计机器人的运动。本文将深入探讨2D和3D SLAM中的各种扫描匹配算法,包括数学原理、实现细节以及实际应用中的性能对比,特别关注…...
