递归时间复杂度分析方法:Master 定理
编写算法时,可能因为对自己代码的复杂度的不清晰而导致错失良机,对于普通的递推或者说循环的代码,仅用简单的调和级数或者等差数列和等比数列即可分析,但是对于递归的代码,简单的递归树法并不方便,理解并记下Master定理,可以让事情变得轻松。
写此文以作笔记,如有错误,请联系博主。
Master 定理基本形式
对于一个递归式 T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac{n}{b}) + f(n) T(n)=aT(bn)+f(n),其中:
- a ≥ 1 a \geq 1 a≥1 和 b > 1 b > 1 b>1 是常数;
- f ( n ) f(n) f(n) 是一个给定的函数,
Master 定理帮助我们确定 T ( n ) T(n) T(n) 的渐进界。
有三种情况:
- 如果 f ( n ) = O ( n c ) f(n) = O(n^c) f(n)=O(nc),其中 c < log b a c < \log_b{a} c<logba, 那么 T ( n ) = Θ ( n log b a ) T(n) = \Theta(n^{\log_b{a}}) T(n)=Θ(nlogba)。
- 如果 f ( n ) = Θ ( n c ) f(n) = \Theta(n^c) f(n)=Θ(nc),其中 c = log b a c = \log_b{a} c=logba, 那么 T ( n ) = Θ ( n c log n ) T(n) = \Theta(n^c\log{n}) T(n)=Θ(nclogn)。
- 如果 f ( n ) = Ω ( n c ) f(n) = \Omega(n^c) f(n)=Ω(nc),其中 c > log b a c > \log_b{a} c>logba,且满足一定的平滑条件(即 a f ( n / b ) ≤ k f ( n ) af(n/b) \leq kf(n) af(n/b)≤kf(n) 对于某个常数 k < 1 k < 1 k<1 和充分大的 n n n), 那么 T ( n ) = Θ ( f ( n ) ) T(n) = \Theta(f(n)) T(n)=Θ(f(n))。
特定的例子
考虑 T ( n ) = 2 T ( n 2 ) + O ( n log n ) T(n) = 2T(\frac{n}{2}) + O(n\log{n}) T(n)=2T(2n)+O(nlogn),这里 a = 2 a = 2 a=2, b = 2 b = 2 b=2, 和 f ( n ) = n log n f(n) = n\log{n} f(n)=nlogn。显然, f ( n ) f(n) f(n) 不符合 Master 定理的标准形式中的 f ( n ) = O ( n c ) f(n) = O(n^c) f(n)=O(nc),因为增长速度比任何 n c n^c nc 形式要快。因此,直接应用标准 Master 定理的三种情况并无法获得解答。
在这种特殊情况下, T ( n ) = 2 T ( n 2 ) + n log n T(n) = 2T(\frac{n}{2}) + n\log{n} T(n)=2T(2n)+nlogn 的时间复杂度实际上是 O ( n ( log n ) 2 ) O(n(\log{n})^2) O(n(logn)2)。如有兴趣请自行查找证明过程。
相关文章:

递归时间复杂度分析方法:Master 定理
编写算法时,可能因为对自己代码的复杂度的不清晰而导致错失良机,对于普通的递推或者说循环的代码,仅用简单的调和级数或者等差数列和等比数列即可分析,但是对于递归的代码,简单的递归树法并不方便,理解并记…...

实例名不规范导致mds创建失败
概述 在部署ceph集群时,规划主机名、关闭防火墙、配置免密、关闭selinux,配置hosts文件这几步同样重要,都是初期部署一次麻烦,方便后续运维的动作。遇到过很多前期稀里糊涂部署,后续运维和配置时候各种坑。 近期遇到…...

OpenGL中的纹理过滤GL_NEAREST和GL_LINEAR
一、GL_NEAREST(最近邻插值) 1.1 原理 当需要从纹理中采样颜色时,GL_NEAREST模式会选择离采样点最近的纹理像素(通常是最接近采样点的纹理元素的中心),并直接使用该像素的颜色值作为输出。这种模式不进行任…...

vue 性能优化
data 层级不要太深 data 层级太深会增加响应式监听的计算,导致页面初次渲染时卡顿。 合理使用 v-show 和 v-if 频繁切换时,使用 v-show无需频繁切换时,使用 v-if 合理使用 computed computed 有缓存,data 不变时不会重新计算&…...
互联网大厂ssp面经(操作系统:part1)
1. 什么是进程和线程?它们之间有什么区别? a. 进程是操作系统中运行的一个程序实例。它拥有独立的地址空间和资源,可以独立执行。 b. 线程是进程内的一个执行单元,一个进程可以包含多个线程。 c. 线程共享进程的资源,…...

Android Activity 启动涉及几个进程
Zygote进程: Zygote进程在Android系统启动时被初始创建,并且初始化了虚拟机(Dalvik或ART),预加载了Android系统的核心类库。所有的Android应用进程都是通过fork()从Zygote进程派生出来的,这允许应用快速启动࿰…...

说说你对链表的理解?常见的操作有哪些?
一、是什么 链表(Linked List)是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的,由一系列结点(链表中每一个元素称为结点)组成 每个结点包括两个部分&…...
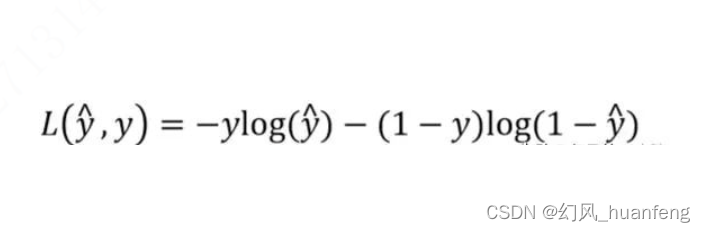
每天五分钟深度学习:逻辑回归算法的损失函数和代价函数是什么?
本文重点 前面已经学习了逻辑回归的假设函数,训练出模型的关键就是学习出参数w和b,要想学习出这两个参数,此时需要最小化逻辑回归的代价函数才可以训练出w和b。那么本节课我们将学习逻辑回归算法的代价函数是什么? 为什么不能平方差损失函数 线性回归的代价函数我们使用…...
llama-factory SFT系列教程 (二),大模型在自定义数据集 lora 训练与部署
文章目录 简介支持的模型列表2. 添加自定义数据集3. lora 微调4. 大模型 lora 权重,部署问题 参考资料 简介 文章列表: llama-factory SFT系列教程 (一),大模型 API 部署与使用llama-factory SFT系列教程 (二),大模型在自定义数…...
:贪吃蛇大作战(多人对战))
C语言游戏实战(11):贪吃蛇大作战(多人对战)
成果展示: 贪吃蛇(多人对战) 前言: 这款贪吃蛇大作战是一款多人游戏,玩家需要控制一条蛇在地图上移动,吞噬其他蛇或者食物来增大自己的蛇身长度和宽度。本游戏使用C语言和easyx图形库编写,旨在…...

腾讯测试岗位的面试经历与经验分享【一面、二面与三面】
腾讯两个月的实习一转眼就结束了,回想起当时面试的经过,感觉自己是跌跌撞撞就这么过了,多少有点侥幸.马上腾讯又要来校招了,对于有意愿想投腾讯测试岗位的同学们,写了一些那时候面试的经历和自己的想法,算不上经验,仅供参考吧! 一面 — —技术基础,全面…...

手机移动端网卡信息获取原理分析
有些场景我们需要获取当前手机上的网卡信息(如双卡双待、Wifi等)。本文准备研究一下这块的原理,以便更好的掌握相关技术原理。 1、底层系统接口 getifaddrs 使用 getifaddrs 接口可以达到我们的目的,该接口会返回本地所有网卡的信…...

无人新零售引领的创新浪潮
无人新零售引领的创新浪潮 在数字化时代加速演进的背景下,无人新零售作为商业领域的一股新兴力量,正以其独特的高效性和便捷性重塑着传统的购物模式,开辟了一条充满创新潜力的发展道路。 依托人脸识别、物联网等尖端技术,无人新…...

SD-WAN提升企业网络体验
在现代企业中,网络体验已成为提升工作效率与业务质量的关键因素。SD-WAN技术的出现,以其独特的优势,为企业提供了优化网络连接、加速数据传输、提升服务质量和应用访问体验,以及增强网络稳定性的解决方案。接下来,我们…...

Docker搭建Let‘s Encrypt
Let’s Encrypt是一个免费、开放和自动化的证书颁发机构(CA),它提供了一种简单、无需重复的机制来获取和更新SSL/TLS证书。Let’s Encrypt Docker镜像允许用户在容器化环境中轻松部署和使用Let’s Encrypt的服务。 主要功能包括:…...

单链表讲解
一.链表的概念以及结构 链表是一种物理结构上不连续,逻辑结构上连续的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。 链表的结构与火车是类似的,一节一节的,数据就像乘客一样在车厢中一样。 与顺序表不同的…...

DFS算法系列 回溯
DFS算法系列-回溯 文章目录 DFS算法系列-回溯1. 算法介绍2. 算法应用2.1 全排列2.2 组合2.3 子集 3. 总结 1. 算法介绍 回溯算法是一种经典的递归算法,通常被用来解决排列问题、组合问题和搜索问题 基本思想 从一个初始状态开始,按一定的规则向前搜索&…...
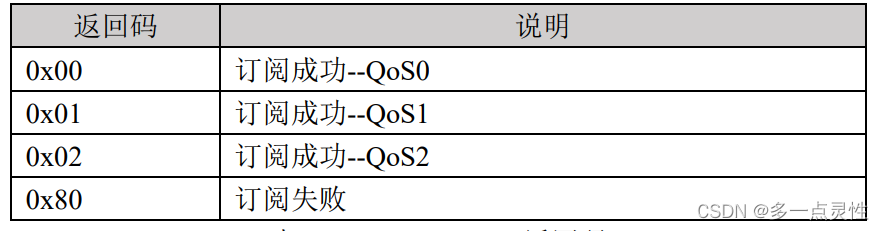
Linux C应用编程:MQTT物联网
1 MQTT通信协议 MQTT(Message Queuing Telemetry Transport,消息队列遥测传 输)是一种基于客户端-服务端架构的消息传输协议,如今,MQTT 成为了最受欢迎的物联网协议,已广泛应用于车联网、智能家居、即时聊…...
企业常用Linux文件命令相关知识+小案例
远程连接工具无法连接VMWARE: 如果发现连接工具有时连不上,ip存在,这时候我们查看网络编辑器,更多配置,看vnet8是不是10段,nat设置是否是正确的? 软件重启一下虚机还原一下网络编辑器 查看文件…...

Istio介绍
1.什么是Istio Istio是一个开源的服务网格(Service Mesh)框架,它提供了一种简单的方式来为部署在Kubernetes等容器编排平台上的微服务应用添加网络功能。Istio的核心功能包括: 服务治理:Istio能够帮助管理服务之间的…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
