DFS算法系列 回溯
DFS算法系列-回溯
文章目录
- DFS算法系列-回溯
- 1. 算法介绍
- 2. 算法应用
- 2.1 全排列
- 2.2 组合
- 2.3 子集
- 3. 总结
1. 算法介绍
回溯算法是一种经典的递归算法,通常被用来解决排列问题、组合问题和搜索问题
基本思想
从一个初始状态开始,按一定的规则向前搜索,当搜索遇到瓶颈无法再前进时,回到当前状态的上一个状态,按照新的要求/条件继续向前搜索,直至所有可用条件都遍历完成。
简单的说就是:不撞南墙不回头
对于回溯算法,其核心就在于不断的"试错",若选择正确则继续往下搜索,否则就"回头"选择另一个选项继续往下搜索。
下面提供一个回溯算法的模板(模板只是对算法理解的总结概况,相较于没有思考的套模板,理解其中的算法思想更加重要–>通过做题积累)
List<List<Integer>> ret;
List<Integer> path; void dfs(int[] nums, ...) {// 满⾜结束条件if (/* 满⾜结束条件 */) {// 将路径添加到结果集中ret.add(new ArrayList<>(path));return;}// 遍历所有选择for (int i = 0;i < nums.size();i++) {// 做出选择path.add(nums[i]); // 做出当前选择后继续搜索dfs(path, nums);// 恢复现场path.remove(path.size() - 1);}
}
其中path用来记录每次选择后改变的路径,nums[i]表示当前做出的选择,并且在当前选择满足递归结束条件后,将当前路径添加到结果集中,结束当前层递归并恢复现场,即恢复刚刚完成修改的路径到上一个状态,才能继续处理当前层的另一个选择,如下图所示:

了解完回溯算法,我们来做一些相关的算法题加深印象!
2. 算法应用
对于回溯(以及DFS相关的题),建议的解题步骤:
- 先画决策树;
- 根据决策树编写函数体,可设置
全局变量、添加剪枝提高效率; - 找到递归出口
2.1 全排列
题目链接:[全排列]
决策树:

代码示例
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;public List<List<Integer>> permute(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[nums.length];dfs(nums);return ret;}void dfs(int[] nums) {if (path.size() == nums.length) {ret.add(new ArrayList(path));return;}for (int i = 0;i < nums.length;i++) { // 这里让i=0,使下一层选项依旧为所有情况(1,2,3,4)if (!check[i]) { // check数组用来记录当前数字是否被使用check[i] = true; path.add(nums[i]); // 将数字添加到路径中dfs(nums);check[i] = false;path.remove(path.size() - 1);}}}
}
2.2 组合
题目链接:[组合]
决策树:

代码示例
class Solution {List<List<Integer>> ret;List<Integer> path;boolean[] check;int len;int pre;public List<List<Integer>> combine(int n, int k) {ret = new ArrayList<>();path = new ArrayList<>();check = new boolean[n + 1];len = k;int[] nums = new int[n + 1];for (int i = 1;i <= n;i++) {nums[i] = i;}dfs(nums, 1);return ret;}public void dfs(int[] nums, int pos) {if (path.size() == len) { // 当路径长度和要求的组合数相等时返回ret.add(new ArrayList<>(path));return;}for (int i = pos;i <= nums.length - 1;i++) { // 这里让i=pos,使下一层选项不会出现当前数字,并且下层选项从pos+1开始if (!check[i]) { path.add(nums[i]); check[i] = true;dfs(nums, i + 1);path.remove(path.size() - 1);check[i] = false;}}}
}
注:这里让i=pos,使下一层选项不会出现当前数字,并且下层选项从pos+1开始;若为i = 0,则使下一层选项依旧为所有情况(1,2,3):

2.3 子集
题目链接:[子集]
决策树:

代码示例
class Solution {static List<List<Integer>> ret;static List<Integer> path;public List<List<Integer>> subsets(int[] nums) {ret = new ArrayList<>();path = new ArrayList<>();dfs(nums, 0);return ret;}public void dfs(int[] nums, int cur) {ret.add(new ArrayList<>(path)); // 此处不设出口目的是将每个节点路径都添加到ret中for (int i = cur;i < nums.length;i++) { // 这里让i=cur,使下一层选项不会出现当前数字,并且下层选项从cur+1开始path.add(nums[i]);dfs(nums, i + 1);path.remove(path.size() - 1); }}
}
3. 总结
总的来说,回溯就是不断的"试错"并回头进行新的选择,和回溯相关的题就要把决策树画出来,通过它来找到我们的递归出口并编写函数体(注意for循环中起始标的使用),注意记得恢复现场哦!
相关文章:

DFS算法系列 回溯
DFS算法系列-回溯 文章目录 DFS算法系列-回溯1. 算法介绍2. 算法应用2.1 全排列2.2 组合2.3 子集 3. 总结 1. 算法介绍 回溯算法是一种经典的递归算法,通常被用来解决排列问题、组合问题和搜索问题 基本思想 从一个初始状态开始,按一定的规则向前搜索&…...
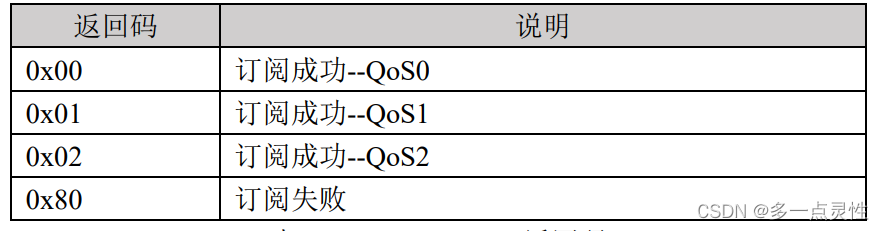
Linux C应用编程:MQTT物联网
1 MQTT通信协议 MQTT(Message Queuing Telemetry Transport,消息队列遥测传 输)是一种基于客户端-服务端架构的消息传输协议,如今,MQTT 成为了最受欢迎的物联网协议,已广泛应用于车联网、智能家居、即时聊…...
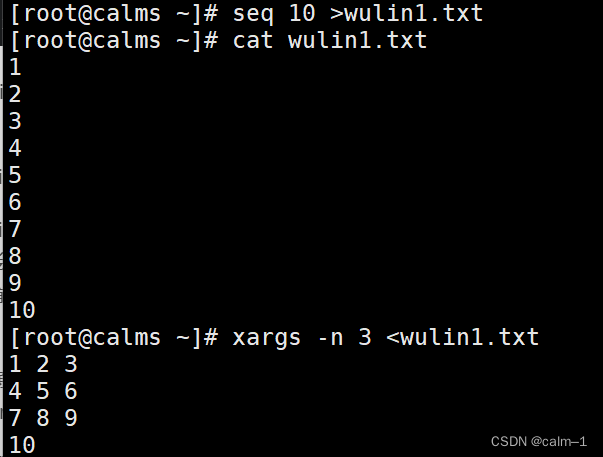
企业常用Linux文件命令相关知识+小案例
远程连接工具无法连接VMWARE: 如果发现连接工具有时连不上,ip存在,这时候我们查看网络编辑器,更多配置,看vnet8是不是10段,nat设置是否是正确的? 软件重启一下虚机还原一下网络编辑器 查看文件…...

Istio介绍
1.什么是Istio Istio是一个开源的服务网格(Service Mesh)框架,它提供了一种简单的方式来为部署在Kubernetes等容器编排平台上的微服务应用添加网络功能。Istio的核心功能包括: 服务治理:Istio能够帮助管理服务之间的…...

代码随想录算法训练营第四十七天|leetcode115、392题
一、leetcode第392题 本题要求判断s是否为t的子序列,因此设置dp数组,dp[i][j]的含义是下标为i-1的子串与下标为j-1的子串相同字符的个数,可得递推公式是通过s[i-1]和t[j-1]是否相等区分。 具体代码如下: class Solution { publ…...

将Ubuntu18.04默认的python3.6升级到python3.8
1、查看现有的 python3 版本 python3 --version 2、安装 python3.8 sudo apt install python3.8 3、将 python3.6 和 3.8 添加到 update-alternatives sudo update-alternatives --install /usr/bin/python3 python3 /usr/bin/python3.6 1 sudo update-alternatives --insta…...
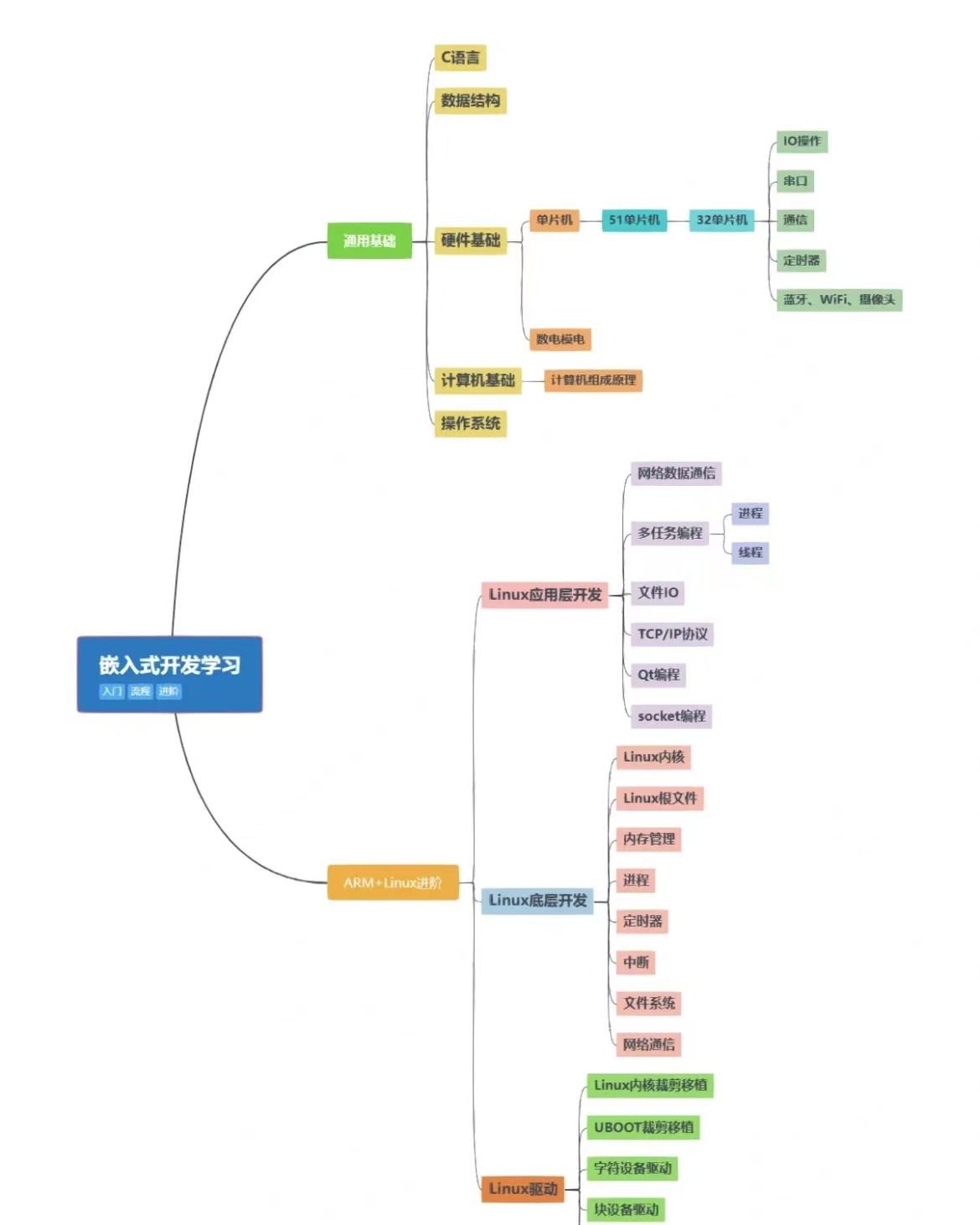
Python和Java哪个更适合后端开发?
Python和Java都是强大的后端开发语言,它们各自有鲜明的特点和适用场景。选择哪一个更适合后端开发,主要取决于具体的项目需求、团队技术栈、个人技能偏好以及长期发展考虑等因素。 下面是两者在后端开发中的优势和劣势: 「Python࿱…...

Python+pytest接口自动化之cookie绕过登录(保持登录状态)
前言 我们今天来聊聊pythonpytest接口自动化之cookie绕过登录(保持登录状态),在编写接口自动化测试用例或其他脚本的过程中,经常会遇到需要绕过用户名/密码或验证码登录,去请求接口的情况,一是因为有时验证…...

什么数据集成(Data Integration):如何将业务数据集成到云平台?
说到数据集成(Data Integration),简单地将所有数据倒入数据湖并不是解决办法。 在这篇文章中,我们将介绍如何轻松集成数据、链接不同来源的数据、将其置于合适的环境中,使其具有相关性并易于使用。 数据集成࿱…...

国外EDM邮件群发多少钱?哪个软件好?
在当今全球化市场环境下,电子邮件营销作为最有效的数字营销渠道之一,其影响力不容忽视。而高效精准的EDM(Electronic Direct Mail)邮件营销策略更是企业拓展海外市场、提升品牌知名度的关键手段。云衔科技以其创新的智能EDM邮件营…...

C语言入门算法——回文数
题目描述: 若一个数(首位不为零)从左向右读与从右向左读都一样,我们就将其称之为回文数。 例如:给定一个十进制数 56,将 56 加 65(即把 56 从右向左读),得到 121 是一个…...

OceanBase—操作实践
文档结构 1、概念简介2、核心设计3、操作实践3.3、数据同步 官方文档:https://www.oceanbase.com/docs/oceanbase-database-cn 1、概念简介 版本分为社区版和企业版,其中企业版兼容MySQL 和Oracle数据库语法; 2、核心设计 存储层 复制层 …...
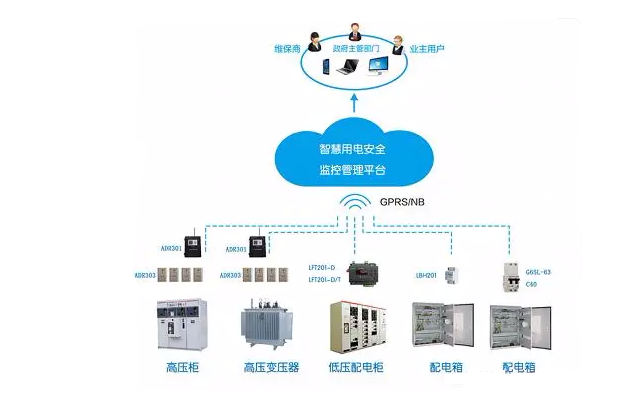
智慧用电安全管理系统
智慧用电安全管理系统 智慧用电安全管理系统是智能电网中客户侧关键的构成部分,是基本建设新型智慧城市的基本,将完成地区内各种各样用电设备的智能化系统监管,完成地区内日常生活与工作中安全性、舒服。 一、智慧用电安全管理系统介绍 …...

Rust语言入门第二篇-Cargo教程
文章目录 Rust语言入门第二篇-Cargo教程一,Cargo 是什么二,Cargo教程Cargo.toml文件src/main.rs 文件构建并运行Cargo项目 Rust语言入门第二篇-Cargo教程 本节提供对cargo命令行工具的快速了解。我们演示了它为我们生成新包的能力,它在包内编…...

测试用例的编写方式
学习目标 能对穷举场景设计测试点能对限定边界规则设计测试点能对多条件依赖关系进行设计测试点能对于项目业务进行设计测试点 目录 等价类划分法案例 等价类划分 说明:在所有测试数据中,具有某种共同特征的数据集合进行划分分类: 有效等…...

HarmonyOS实战开发-状态管理、通过使用页面级的状态变量 和应用级的状态变量 来实现应用的状态管理。
介绍 本示例通过使用页面级的状态变量 和应用级的状态变量 来实现应用的状态管理。 效果预览 使用说明 1.点击首页中的基本类型进入对应页面,点击按钮可以更改圆形的颜色;点击查看源码可以展示基本类型功能效果的源码。 2.点击首页中的数组类型进入对…...

【Java开发指南 | 第二篇】标识符、Java关键字及注释
专栏:Java开发指南 CSDN秋说 文章目录 标识符Java关键字Java注释 标识符 Java 所有的组成部分都需要名字。类名、变量名以及方法名都被称为标识符。 所有的标识符都应该以字母(A-Z 或者 a-z),美元符($)、或者下划线&…...

3D可视化技术:研发基地的科技新篇章
在科技日新月异的今天,我们生活在一个充满无限可能性的时代。而在这个时代中,3D可视化技术正以其独特的魅力,引领着科技领域的新一轮变革。 3D可视化技术通过三维图像的方式,将现实世界或虚拟世界中的物体、场景等以立体、逼真的形…...

蓝旭前端05:JavaScript进阶
蓝旭前端05:JavaScript进阶 基础简单复习 数据类型 基本数据类型:Number、String、Boolean、Null、Undefined等。引用数据类型:Object、Array、Function等。typeof操作符:返回数据类型的字符串形式。 变量 变量声明࿱…...

【docker-compose】安装及配置
目录 安装在线安装离线安装 配置mysql5.7bitnami/mysql8.3redisweb前后台分离部署前端https(SSL)配置nginx动态传参资源限制:内存、cpunacossentinelgateway 问题汇总iptables No chain/target/match by that namedocker-compose.yml修改mysql密码,重启后…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
