数据结构排序算法
排序也称排序算法(SortAlgorithm),排序是将一组数据,依指定的顺序进行排列的过程。
分类
- 内部排序【使用内存】
- 指将需要处理的所有数据都加载到内部存储器中进行排序
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 简单选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 基数排序
- 外部排序法【使用内存和外存结合】
- 数据量过大,无法全部加载到内存中,需要借助外部存储(文件等)进行排序
时间复杂度
度量一个程序(算法)执行时间的两种方法
- 事后统计的方法
- 这种方法可行,但是有两个问题:一是要想对设计的算法的运行性能进行评测,需要实际运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素,这种方式,要在同一台计算机的相同状态下运行,才能比较那个算法速度更快。
- 事前估算的方法
- 通过分析某个算法的时间复杂度来判断哪个算法更优
基本概念
-
时间频度
- 一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为 T ( n ) T(n) T(n)。
- 对于时间频度而言
- 常数项是可以忽略的
- 如: T ( n ) = 2 n + 10 T(n)=2n+10 T(n)=2n+10 和 T ( n ) = 2 n T(n)=2n T(n)=2n的值是无限接近的
- 低次项是可以忽略的
- 如: T ( n ) = 2 n 2 + 3 n + 10 T(n)=2n^2+3n+10 T(n)=2n2+3n+10 和 T ( 2 n 2 ) T(2n^2) T(2n2) 无限接近
- 系数项在一定情况下可忽略
- 随着n值变大, 5 n 2 + 7 n 5n^2+7n 5n2+7n 和 3 n 2 + 2 n 3n^2+2n 3n2+2n,执行曲线重合,说明这种情况下,5和3可以忽略。
- 而 n 3 + 5 n n^3+5n n3+5n 和 6 n 3 + 4 n 6n^3+4n 6n3+4n,执行曲线分离,说明多少次方式关键,此时系数项不可忽略,且结果比例无限接近 1:6
- 常数项是可以忽略的
-
时间复杂度
- 一般情况下,算法中的基本操作语句的重复执行次数是问题规模 n n n的某个函数,用 T ( n ) T(n) T(n)表示,若有某个辅助函数 f ( n ) f(n) f(n),使得当 n 趋近于无穷大时, T ( n ) f ( n ) \frac{T(n)}{f(n)} f(n)T(n)的极限值为不等于零的常数1,则称 f ( n ) f(n) f(n)是 T ( n ) T(n) T(n)的同数量级函数。记作 T ( n ) = O ( f ( n ) ) T(n)=O(f(n)) T(n)=O(f(n)),称 O ( f n ) O(fn) O(fn) 为算法的渐进时间复杂度,简称时间复杂度。
- T ( n ) T(n) T(n)不同,但时间复杂度可能相同。如: T ( n ) = n 2 + 7 n + 6 T(n)=n^2+7n+6 T(n)=n2+7n+6 与 T ( n ) = 3 n 2 + 2 n + 2 T(n)=3n^2+2n+2 T(n)=3n2+2n+2 它们的 T ( n ) T(n) T(n)不同,但时间复杂度相同,都为 O ( n 2 ) O(n^2) O(n2)
- 计算时间复杂度的方法:
- 用常数1代替运行时间中的所有加法常数 T ( n ) = 3 n 2 + 2 n + 2 T(n)=3n^2+2n+2 T(n)=3n2+2n+2 ➡️ T ( n ) = 3 n 2 + 2 n + 1 T(n)=3n^2+2n+1 T(n)=3n2+2n+1
- 修改后的运行次数函数中,只保留最高阶项 T ( n ) = 3 n 2 + 2 n + 1 T(n)=3n^2+2n+1 T(n)=3n2+2n+1 ➡️ T ( n ) = 3 n 2 T(n)=3n^2 T(n)=3n2
- 去除 最高阶项的系数 T ( n ) = 3 n 2 T(n)=3n^2 T(n)=3n2 ➡️ T ( n ) = n 2 T(n)=n^2 T(n)=n2 ➡️ O ( n 2 ) O(n^2) O(n2)
常见的时间复杂度
-
常数阶 O ( 1 ) O(1) O(1)
无论代码执行了多少行,只要没有循环等复杂结构,那这个代码的时间复杂度就都是 O ( 1 ) O(1) O(1)2
-
对数阶 O ( log 2 n ) O(\log_2n) O(log2n)
int i = 1; while(i<n) {i = i * 2; }在while循环里面,每次都将i乘以2,乘完之后,i距离n就越来越近了。假设循环x次之后,i就大于2了,此时这个循环就退出了,也就是说2的 x x x 次方等于n,那么 x = log 2 n x=\log_2n x=log2n也就是说当循环 log 2 n \log_2n log2n次以后,这个代码就结束了。因此这个代码的时间复杂度为: O ( log 2 n ) O(\log_2n) O(log2n)。 O ( log 2 n ) O(\log_2n) O(log2n)的这个2时间上是根据代码变化的,i=i*3,则是 O ( log 3 n ) O(\log_3n) O(log3n).
-
线性阶 O ( n ) O(n) O(n)
for(int i = 0; i <= n; ++i) {j = i;j++; }这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用 O ( n ) O(n) O(n)来表示它的时间复杂度
-
线性对数阶 O ( n log 2 n ) O(n\log_2{n}) O(nlog2n)
for(m=1; m < n; m++) {i = 1;while(i < n) {i = i * 2;} }线性对数阶 O ( n log 2 N ) O(n\log_2N) O(nlog2N)其实非常容易理解,将时间复杂度为 O ( log 2 n ) O(\log_2n) O(log2n)的代码循环N遍的话,那么它的时间复杂度就是 n ∗ O ( log 2 N ) n*O(\log_2N) n∗O(log2N),也就是了 O ( n log 2 N ) O(n\log_2N) O(nlog2N)
-
平方阶 O ( n 2 ) O(n^2) O(n2)
for(x = 1; i <= n; x++) {for(i = 1; i <= n; i++) {j = i;j++} }平方阶 O ( n 2 ) O(n^2) O(n2)就更容易理解了,如果把 O ( n ) O(n) O(n)的代码再嵌套循环一遍,它的时间复杂度就是 O ( n 2 ) O(n^2) O(n2),这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O ( n ∗ n ) O(n*n) O(n∗n),即 O ( n 2 ) O(n^2) O(n2)如果将其中一层循环的n改成m,那它的时间复杂度就变成了O(m*n)
-
立方阶 O ( n 3 ) O(n^3) O(n3)
-
k次方阶 O ( n k ) O(n^k) O(nk)
-
指数阶 O ( 2 n ) O(2^n) O(2n)
常见的算法时间复杂度从小到大依次增加,其中 O ( n ! ) > O ( 2 n ) O(n!)>O(2^n) O(n!)>O(2n),随着问题规模 n n n的不断增大,上述时间复杂度不断增大,算法的执行效率越来越低,在日常开发中应尽可能避免使用指数阶的算法
平均时间复杂度和最坏时间复杂度
- 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下,
该算法的运行时间。 - 最坏情况下的时间复杂度称最坏时间复杂度。一般讨论的时间复杂度
均是最坏情况下的时间复杂度。这样做的原因是:最坏情况下的时间复杂度是算法在任何输入实例上运行时间的界限,这就保证了算法的运行时间不会比最坏情况更长。 - 平均时间复杂度和最坏时间复杂度是否一致,和算法有关
| 排序 | 平均时间 | 最差情况 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 稳定 | O ( 1 ) O(1) O(1) | n小时较好 |
| 交换 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( 1 ) O(1) O(1) | n小时较好 |
| 选择 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( 1 ) O(1) O(1) | n小时较好 |
| 插入 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | 稳定 | O ( 1 ) O(1) O(1) | 大部分已排序时较好 |
| 基数 | O ( log R B ) O(\log_RB) O(logRB) | O ( log R B ) O(\log_RB) O(logRB) | 稳定 | O ( n ) O(n) O(n) | B是真数(0-9) R是基数(个十百) |
| Shell | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | O ( n s ) 1 < s < 2 O(n^s)1<s<2 O(ns)1<s<2 | 不稳定 | O ( 1 ) O(1) O(1) | s是所选分组 |
| 快速 | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | O ( n 2 ) O(n^2) O(n2) | 不稳定 | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | n大时较好 |
| 归并 | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | 稳定 | O ( 1 ) O(1) O(1) | n大时较好 |
| 堆 | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | O ( n log 2 n ) O(n\log_2n) O(nlog2n) | 不稳定 | O ( 1 ) O(1) O(1) | n大时较好 |
空间复杂度
- 类似于时间复杂度的讨论,一个算法的空间复杂度(Space Complexity)定义为该算法所耗费的存储空间,它也是问题规模的函数。
- 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模有关,它随着n的增大而增大,当较大时,将占用较多的存储单元,例如快速排序和归并排序算法,基数排序就属于这种情况
- 在做算法分析时,主要讨论的是时间复杂度。从用户使用体验上看,更看重的程序执行的速度。一些缓存产品(redis,memcache)和算法(基数排序)本质就是用空间换时间.
测试代码运行时间
// 创建80000个随机的数组
int[] arr2 = new int[80000];
for (int i = 0; i < 80000; i++) {arr2[i] = (int) (Math.random() * 8000000);
}Date date1 = new Date();
SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM--dd HH:mm:ss");
String date1Str = simpleDateFormat.format(date1);
System.out.println("排序前时间="+date1Str);selectSort(arr2); // 选择排序
// BufferSort(arr2); // 冒泡排序Date date2 = new Date();
SimpleDateFormat simpleDateFormat2 = new SimpleDateFormat("yyyy-MM--dd HH:mm:ss");
String date2Str = simpleDateFormat2.format(date2);
System.out.println("排序前时间="+date2Str);
冒泡排序
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就象水底下的气泡一样逐渐向上冒
因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志 flag 判断元素是否进行过交换。从而减少不必要的比较。
// 冒泡排序 时间复杂度 O(n^2)
public static void BufferSort(int[] arr) {int temp = 0;// 标识变量,表示是否进行过交换boolean flag = false;for (int i = 0; i < arr.length - 1; i++) {for (int j = 0; j < arr.length - 1 - i; j++) {if (arr[j] > arr[j + 1]) {flag = true;temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}System.out.printf("第%d次循环:", i + 1);System.out.println(Arrays.toString(arr));if (!flag) {// 在一趟排序中,一次交换都没有发生过break;} else {flag = false; // 重置flag}}
}
选择排序
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从arr[0] ~ arr[n-1]中选取最小值,与arr[0]交换,第二次从arr[1] ~ arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2] ~ arr[n-1]中选取最小值,与arr[2]交换,…,第i次从arr[i-1] ~ arr[n-1]中选取最小值,与arr[i-1]交换,…,第n-1次从arr[n-2] ~ arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
// 选择排序 时间复杂度 O(n^2)
public static void selectSort(int[] arr) {for (int i = 0; i < arr.length - 1; i++) {int minIndex = i; // 最小值索引int min = arr[i]; // 最小值for (int j = i + 1; j < arr.length; j++) {if (min > arr[j]) {// 说明假定的最小值不是最小min = arr[j]; // 重置minminIndex = j; // 重置minIndex}}// 交换位置if (minIndex != i) {arr[minIndex] = arr[i];arr[i] = min;}System.out.printf("第%d次循环:", i + 1);System.out.println(Arrays.toString(arr));}
}
插入排序
插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
插入排序(Insertion Sorting)的基本思想是:把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。
缺点:当需要插入的数是较小的数时,后移的次数明显增多,对效率有影响,可用希尔排序优化
// 插入排序
public static void insertSort(int[] arr) {for (int i = 1; i < arr.length; i++) {// 定义待插入的数int insertVal = arr[i];int insertIndex = i - 1; // 即arr[1]的前面这个数的下标// 给insertVal 找插入的位置// insertIndex >= 0 保证在给insertVal 找插入位置时不越界// insertVal < arr[insertIndex] 待插入的数,还没有找到插入位置while (insertIndex >= 0 && insertVal < arr[insertIndex]) {arr[insertIndex + 1] = arr[insertIndex]; // arr[insertIndex] 后移insertIndex--;}// 当退出while循环时,说明插入的位置找到,insertIndex + 1if (insertIndex + 1 != i) {// 如果待插入值大于前一位值,则 insertIndex + 1 != i但是多了判读时间+交换时间,因此可加可不加arr[insertIndex + 1] = insertVal;}System.out.printf("第%d次循环:", i);System.out.println(Arrays.toString(arr));}
}
希尔排序
希尔排序是希尔(Donald Shell)于I959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序:随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止
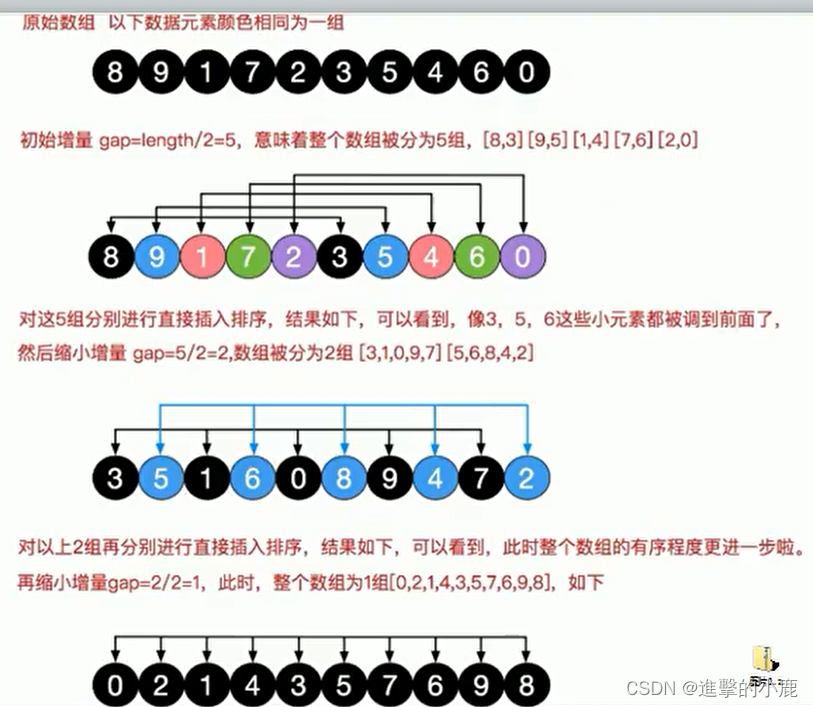
交换法
比较值,一发现大小关系直接交换
希尔排序时,对有序序列在插入时采用交换法,速度较慢
// 希尔排序 -- 交换法
public static void shellSort(int[] arr) {int temp = 0;int count = 0; // 计数器【可不写】// 增量gap,并逐步的缩小增量for (int gap = arr.length / 2; gap > 0; gap /= 2) {for (int i = gap; i < arr.length; i++) {// 遍历各组中所有的元素(共gap组,每组有 x(按实际来分) 个元素),步长gapfor (int j = i - gap; j >= 0; j -= gap) {// 如果当前元素大于加上步长后的哪个元素,说明需要交换【从小到大】if (arr[j] > arr[j + gap]) {temp = arr[j];arr[j] = arr[j + gap];arr[j + gap] = temp;}}}System.out.printf("希尔排序第%d次循环:", ++count);System.out.println(Arrays.toString(arr));}}
移动法
比较值,发现关系大小时先不交换,后移值,继续比较,当找到合适的位置时再插入
希尔排序时,对有序序列在插入时采用移动法,速度快,推荐使用
希尔排序快的主要原因不在于数据的操作方式,而在于宏观调控
// 希尔排序 -- 移位法
public static void shellSort2(int[] arr) {int temp = 0;int count = 0; // 计数器【可不写】// 增量gap,并逐步的缩小增量for (int gap = arr.length / 2; gap > 0; gap /= 2) {// 从第gap个元素,逐个对其所在的组进行直接插入排序for (int i = gap; i < arr.length; i++) {int j = i;temp = arr[j];if (arr[j] < arr[j - gap]) {while (j - gap >= 0 && temp < arr[j - gap]) {// 后 移动arr[j] = arr[j - gap];j -= gap;}// 当退出while后,就给temp找到插入的位置arr[j] = temp;}}System.out.printf("希尔排序第%d次循环:", ++count);System.out.println(Arrays.toString(arr));}
}
快速排序法
快速排序(Quicksort)是对冒泡排序的一种改进。
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
// 快速排序法1
public static void quickSort1(int[] arr, int left, int right) {int l = left; // 左下标int r = right; // 右下标int pivot = arr[(left + right) / 2];int temp = 0; // 临时变量// while循环目的是让比pivot 值小的放到左边,大的放右边while (l < r) {// 在pivot 的左边一直找,直到找到大于等于pivot 值才退出while (arr[l] < pivot) {l += 1;}// 在pivot 的右边一直找,直到找到小于等于pivot 值才退出while (arr[r] > pivot) {r -= 1;}// 如果l >= r说明pivot 的左右两的值,已经按照左边全部是// 小于等手pivot值,右边全部是大于等于pivot值if (l >= r) {break;}// 交换temp = arr[l];arr[l] = arr[r];arr[r] = temp;// 如果交换完后发现这个arr[l] == pivot ,则 r 前移,r--if (arr[l] == pivot) {r -= 1;}// 如果交换完后发现这个arr[r] == pivot ,则 l 后移,l++if (arr[r] == pivot) {l += 1;}}// 如果 l == r,必须l++,r--,否则出现栈溢出if (l == r) {l += 1;r -= 1;}// 向左递归if (left < r) {quickSort1(arr, left, r);}// 向右递归if (right > l) {quickSort1(arr, l, right);}
}
// 快速排序法2
public static void quickSort2(int[] arr, int start, int end) {if (start < end) {// 标准数int stard = arr[start];// 记录下标int low = start;int high = end;// 循环找比标准数大的数和比标准数小的数while (low < high) {// 右边的数字比标准数大while (low < high && stard <= arr[high]) {high--;}// 使用右边的数字替换左边的数arr[low] = arr[high];// 如果左边的数字比标准数小while (low < high && arr[low] <= stard) {low++;}arr[high] = arr[low];}// 把标准数付给低位或高位arr[low] = stard;// 递归// 处理所有小的数字quickSort2(arr, start, low);// 处理所有大的数字quickSort2(arr, low + 1, end);}
}
// 快速排序法3
public static void quickSort3(int[] arr, int low, int high) {int i, j, stard, t;if (low > high) {return;}i = low;j = high;//temp就是基准位stard = arr[low];while (i < j) {//先看右边,依次往左递减while (stard <= arr[j] && i < j) {j--;}//再看左边,依次往右递增while (stard >= arr[i] && i < j) {i++;}//如果满足条件则交换if (i < j) {t = arr[j];arr[j] = arr[i];arr[i] = t;}}//最后将基准为与i和j相等位置的数字交换arr[low] = arr[i];arr[i] = stard;//递归调用左半数组quickSort3(arr, low, j - 1);//递归调用右半数组quickSort3(arr, j + 1, high);
}
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是 O ( N 2 ) O(N_2) O(N2),它的平均时间复杂度为 O ( N log 2 N ) O(N\log_2N) O(Nlog2N)。其实快速排序也是基于一种叫做“二分”的思想。
归并排序
归并排序(MERGE-SOT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
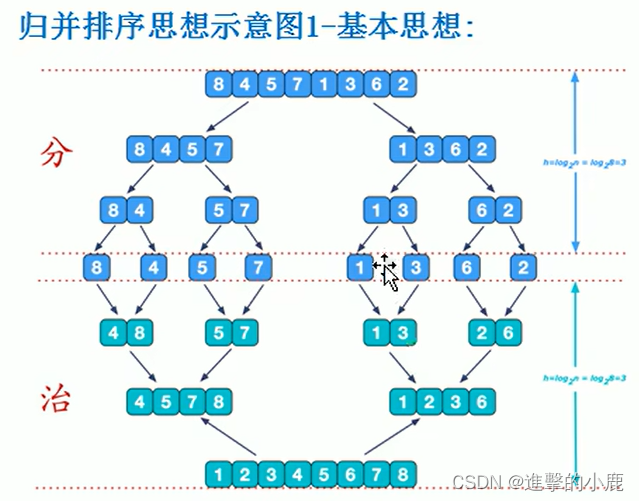
// 归并排序 - 分+合
public static void mergeSort(int[] arr, int left, int right, int[] temp) {if (left < right) {int mid = (left + right) / 2; // 中间索引// 向左递归进行分解mergeSort(arr, left, mid, temp);// 向右递归进行分解mergeSort(arr, mid + 1, right, temp);// 合并merge(arr, left, mid, right, temp);}
}// 归并排序 - 合
/*** @param arr 原始数组* @param left 左边有序序列的初始索引* @param mid 中间索引* @param right 右边索引* @param temp 做中转的数组*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {int i = left; // 初始化i,左边有序序列的初始索引int j = mid + 1; // 初始化j,右边有序序列的初始索引int t = 0; // 指向temp数组的当前索引// 1、先把左右两边(有序)的数据按照规则填充到temp数组// 直到左右两边的有序序列,有一边处理完毕为止while (i <= mid && j <= right) {// 如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素// 即将左边的当前元素,填充到temp数组// 然后 t++,i++if (arr[i] <= arr[j]) {temp[t] = arr[i];t += 1;i += 1;} else { // 反之亦然temp[t] = arr[j];t += 1;j += 1;}}// 2、把有剩余数据的一边的数据依次全部填充到tempwhile (i <= mid) { // 左边的有序序列还有剩余的元素,就全部填充到temptemp[t] = arr[i];t += 1;i += 1;}while (j <= right) { // 右边的有序序列还有剩余的元素,就全部填充到temptemp[t] = arr[j];t += 1;j += 1;}// 3、将temp数组的元素拷贝到arr// 但不是每次都拷贝所有值t = 0;int tempLeft = left;System.out.println("tempLeft=" + tempLeft + "\tright=" + right);while (tempLeft <= right) {arr[tempLeft] = temp[t];t += 1;tempLeft += 1;}
}
合并的次数为数组长度-1
基数排序
空间换时间的经典算法,速度较快,具体速度看规模
- 基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用
- 基数排序法是属于稳定性的排序,基数排序法的是效率高的稳定性排序法
- 基数排序(Radix Sort)是桶排序的扩展
- 基数排序是1887年赫尔曼何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
- 基数排序是对传统桶排序的扩展,速度很快
- 基数排序是经典的空间换时间的方式,占用内存很大,当对海量数据排序时,容易造成OutOfMemoryError
- 基数排序时稳定的。[注:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i] = r[j],且r[i] 在r[j] 之前,而在排序后的序列中,r[i] 仍在r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的]
- **注意:**如果有负数的数组,一般不用基数排序来进行排序
基本思路
将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
第1轮排序:
- 将每个元素的个位数取出,然后看这个数应该放在哪个对应下标的桶【会先创建十个桶】(一个桶对应一个一维数组)
- 按照这个桶的顺序(从一维数组的下标依次取出数据,放入到原来的数组中)
第2轮排序:
- 将每个元素的十位数取出,然后看这个数应该放在哪个对应下标的桶(一个桶对应一个一维数组)
- 按照这个桶的顺序(从一维数组的下标依次取出数据,放入到原来的数组中)
第3轮排序:
- 将每个元素的百位数取出,然后看这个数应该放在哪个对应下标的桶(一个桶对应一个一维数组)
- 按照这个桶的顺序(从一维数组的下标依次取出数据,放入到原来的数组中)
…
// 基数排序【空间换时间的算法】
public static void radixSort(int[] arr) {// 得到数组中最大的位数int max = arr[0];for (int i = 1; i < arr.length; i++) {if (arr[i] > max) {max = arr[i];}}// 得到最大数的位数int maxLength = (max + "").length();// 定义一个二维数组,表示10个桶,每个桶就是一个一维数组// 为了防止放入数时数据溢出,因此每个桶大小定位arr.lengthint[][] bucket = new int[10][arr.length];int[] bucketElementCounts = new int[10]; // 记录每个桶放入的数据个数for (int i = 0, n = 1; i < maxLength; i++, n *= 10) {// 针对每个元素对应位进行排序处理,第一次是个位,第二次是十位,第三次是百位......// 循环取出数组放入桶中for (int j = 0; j < arr.length; j++) {// 取出每个元素的个位的值int digitOfElement = arr[j] / n % 10;// 放入到对应的桶中bucket[digitOfElement][bucketElementCounts[digitOfElement]] = arr[j];bucketElementCounts[digitOfElement]++; // 更新记录桶的数据个数}// 按照这个桶的顺序(一维数组的下标依次取出数据,放入到原来的数组中)int index = 0;// 遍历每一桶,并将桶中的数据放入到原数组for (int k = 0; k < bucket.length; k++) {// 如果桶中有数据才放入到原数组if (bucketElementCounts[k] != 0) {// 循环该桶,即第k个桶放入for (int l = 0; l < bucketElementCounts[k]; l++) {// 取出元素放入到arrarr[index++] = bucket[k][l];}}// 第l轮处理后,需要清空每个 bucketElementCounts[k] 的值bucketElementCounts[k] = 0;}System.out.println("第" + (i + 1) + "轮,排序处理 arr=" + Arrays.toString(arr));}}
补充
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在兹盘中,而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度:一个算法执行所耗费的时间。
- 空间复杂镀:运行完一个程序所需内存的大小。
- n:数据规模
- k:“桶”的个数
- In-place:不占用额外内存
- Out-place:占用额外内存
当 T ( n ) f ( n ) \frac{T(n)}{f(n)} f(n)T(n)的值无限趋近于 1 1 1时,此时 f ( n ) = O ( 1 ) f(n)=O(1) f(n)=O(1) ↩︎
代码在执行的时候,当它消耗的时间并不随着某个变量的增长而增长,那么无论代码多长,都可以用 O ( 1 ) O(1) O(1)表示它的时间复杂度 ↩︎
相关文章:

数据结构排序算法
排序也称排序算法(SortAlgorithm),排序是将一组数据,依指定的顺序进行排列的过程。 分类 内部排序【使用内存】 指将需要处理的所有数据都加载到内部存储器中进行排序插入排序 直接插入排序希尔排序 选择排序 简单选择排序堆排序 交换排序 冒泡排序快速…...

【深度剖析】曾经让人无法理解的事件循环,前端学习路线
先自我介绍一下,小编浙江大学毕业,去过华为、字节跳动等大厂,目前阿里P7 深知大多数程序员,想要提升技能,往往是自己摸索成长,但自己不成体系的自学效果低效又漫长,而且极易碰到天花板技术停滞…...
Spring 事务失效总结
前言 在使用spring过程中事务是被经常用的,如果不小心或者认识不做,事务可能会失效。下面列举几条 业务代码没有被Spring 容器管理 看下面图片类没有Componet 或者Service 注解。 方法不是public的 Transactional 注解只能用户public上,…...

K8S节点kubectl命令报错x509: certificate signed by unknown authority
K8S节点上执行kubectl get node命令报错证书问题,查看kubelet日志如下 [localhost10 ~]$ journalctl -xeu kubelet --since "2024-04-09" --no-pager 4月 09 00:06:22 10.10.44.23-v7-prod-cams-08 kubelet[2142]: I0409 00:06:22.150535 2142 csi_pl…...

【HTML】制作一个简单的实时字体时钟
目录 前言 HTML部分 CSS部分 JS部分 效果图 总结 前言 无需多言,本文将详细介绍一段HTML代码,具体内容如下: 开始 首先新建文件夹,创建一个文本文档,两个文件夹,其中HTML的文件名改为[index.html]&am…...
servlet的三个重要的类(httpServlet 、httpServletRequst、 httpServletResponse)
一、httpServlet 写一个servlet代码一般都是要继承httpServlet 这个类,然后重写里面的方法 但是它有一个特点,根据之前写的代码,我们发现好像没有写main方法也能正常执行。 原因是:这个代码不是直接运行的,而是放到…...
【软考】设计模式之命令模式
目录 1. 说明2. 应用场景3. 结构图4. 构成5. 优缺点5.1 优点5.2 缺点 6. 适用性7.java示例 1. 说明 1.命令模式(Command Pattern)是一种数据驱动的设计模式。2.属于行为型模式。3.请求以命令的形式被封装在对象中,并传递给调用对象。4.调用对…...

波奇学Linux:ip协议
ip报头是c语言的结构体 报头和有效载荷如何分离? 固定长度四位首部长度 4位版本号就是IPV4 8位服务类型:4位TOS位段和位保留字段 4位TOS分别表示:最小延时,最大吞吐量,最高可靠性,最小成本 给路由器提…...
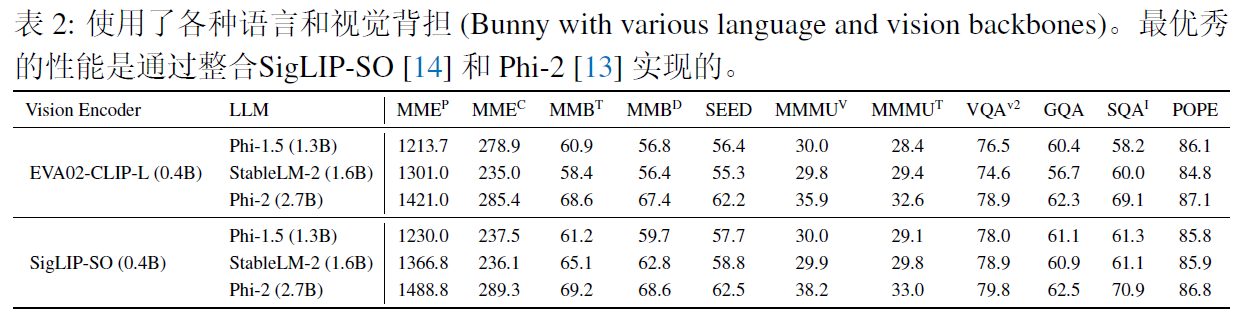
Efficient Multimodal learning from data-centric perspective
[MLLM-小模型推荐-2024.3.18] Bunny 以数据的眼光看问题 - 知乎近期几天会梳理下多模态小模型相关的论文,做个汇总。为了能够每天更新点啥,先穿插一些小模型算法。等到全部算法都梳理完成后,再发布一篇最终汇总版本的。 3.15 号 BAAI 发布了 …...

ubuntu下交叉编译ffmpeg到目标架构为aarch架构的系统
Ubuntu下FFmpeg的aarch64-linux-gnu架构交叉编译教程 一、前言 有时候真的很想报警的,嵌入式算法部署花了好多时间了,RKNN 1808真是问题不少;甲方那边也是老是提新要求,真是受不了。 由于做目标检测,在C代码中有对视…...

【Linux C | 多线程编程】线程同步 | 条件变量(万字详解)
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 ⏰发布时间⏰:2024-04-15 0…...

【高阶数据结构】哈希表 {哈希函数和哈希冲突;哈希冲突的解决方案:开放地址法,拉链法;红黑树结构 VS 哈希结构}
一、哈希表的概念 顺序结构以及平衡树 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系。因此在查找一个元素时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N);平衡树中为树的高度,即O(log_2 N)…...
)
嵌入式之计算机网络篇(七)
七、计算机网络 1.说说计算机网络五层体系结构 计算机网络的五层架构包括应用层、传输层、网络层、数据链路层和物理层。 应用层:是网络结构中的最高层,负责向用户提供网络服务,如文件传输、电子邮件、远程登录等。常见的应用层协议有HTTP…...
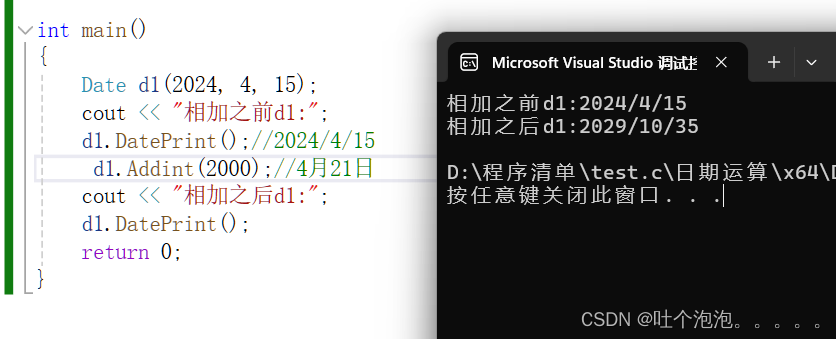
C++|运算符重载(1)|为什么要进行运算符重载
写在前面 本篇里面的日期类型加法,先不考虑闰年,平年的天数,每月的天数统一按30天算,那么每一年也就是360天 目录 写在前面 定义 基本数据类型 自定义数据类型 成员函数解决相加问题 Date类+整形 下一篇----运…...
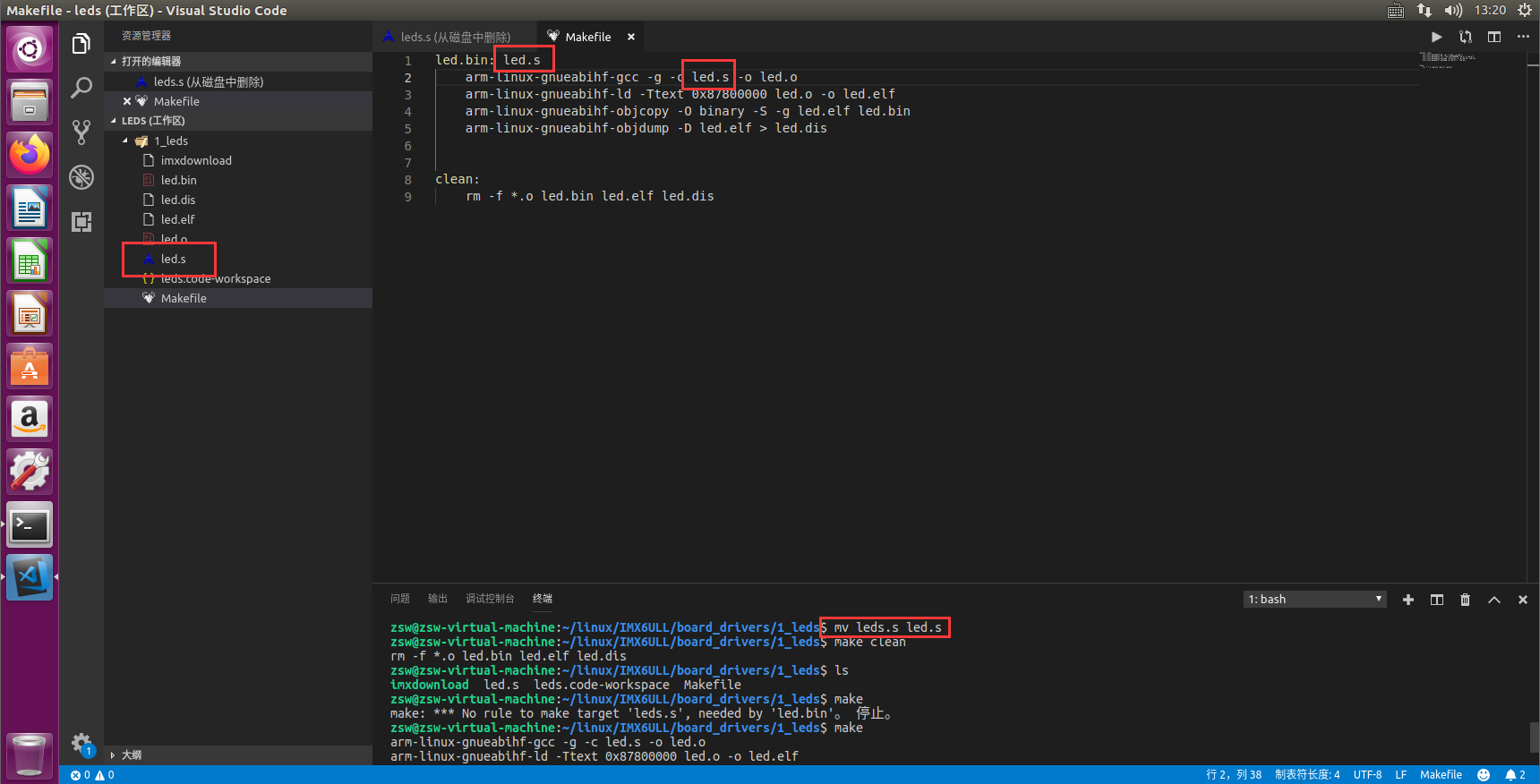
【ARM 裸机】汇编 led 驱动之烧写 bin 文件
1、烧写概念 bin 文件烧写到哪里呢?使用 STM32 的时候烧写到内部 FLASH,6ULL 没有内部 FLASH,是不是就不能烧写呢?不,6ULL 支持 SD卡、EMMC、NAND FLASH、NOR FLASH 等方式启动,在裸机学习的工程中&#x…...

计算机网络之CIDR
快速了解CIDR CIDR 表示的是什么? 单个IP地址:当你看到一个CIDR表示法,如192.168.1.1/32,它表示一个单独的具体IP地址。/32表示所有32位都是网络部分,没有主机部分,因此它指的是单一的IP地址。 一个IP地址…...
【无标题】系统思考—智慧共赢座谈会
第432期JSTO—“智慧共赢座谈会”精彩回顾 我们身处一个快速变化的世界,其中培训和咨询行业也不断面临新的挑战和机遇。为了紧跟这些变革,我们邀请了行业专家与合作伙伴深入探讨在培训、交付和销售过程中遇到的难题。 本次座谈会的亮点之一是我们科学上…...

【Linux C | 多线程编程】线程同步 | 互斥量(互斥锁)介绍和使用
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 ⏰发布时间⏰: 本文未经允许…...

mid_360建图和定位
录制数据 roslaunch livox_ros_driver2 msg_MID360.launch使用fast-lio 建图 https://github.com/hku-mars/FAST_LIO.git 建图效果 使用python做显示 https://gitee.com/linjiey11/mid360/blob/master/show_pcd.py 使用 point_lio建图 https://github.com/hku-mars/Point…...

ThreadX在STM32上的移植:通用启动文件tx_initialize_low_level.s
在嵌入式系统开发中,实时操作系统(RTOS)的选择对于系统性能和稳定性至关重要。ThreadX是一种广泛使用的RTOS,它以其小巧、快速和可靠而闻名。在本文中,我们将探讨如何将ThreadX移植到STM32微控制器上,特别是…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
