XCPC第九站———背包问题!

1.01背包问题

我们首先定义一个二维数组f,其中f[i][j]表示在前i个物品中取且总体积不超过j的取法中的最大价值。那么我们如何得到f[i][j]呢?我们运用递推的思想。由于第i个物品只有选和不选两种情况,当不选第i个物品时,f[i][j]=f[i-1][j],即取前i-1个物品且总体积小于等于j的所有取法中的最大价值;当选第i个物品时,我们要为第i个物品留出空间,此时f[i][j]=f[i-1][j-v[i]]+wi,即取前i-1个物品且总体积不能超过j-v[i]的取法中的最大价值再加上第i个物品的价值。因此代码如下:
#include<iostream>
#include<cmath>
using namespace std;
const int K = 1010;int v[K],w[K],f[K][K];int main()
{//本来应该对f[0][0~V]进行初始化为0,但由于我们开的数组是全局变量,自动初始化为0,因此这一步省略了。int N,V;cin>>N>>V;//一定要从下标1开始读入数据,因为后面是从下标1开始遍历物品的,如果从下标0开始读入,会遗漏第一个物品。for(int i = 1;i<=N;i++) cin>>v[i]>>w[i];//由于i-1应该大于等于0,所以从i=1开始遍历。for(int i = 1;i<=N;i++){for(int j = 0;j<=V;j++){//只有在j>=v[i],即能放得下第i个物品的时候我们才有第二种情况。因此我们不妨直接先让f[i][j]继承f[i-1][j],然后再在满足条件时取两者中的最大值即可。f[i][j] = f[i-1][j];if(j>=v[i])f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);}}cout<<f[N][V]<<endl;return 0;
}那么我们如何对代码进行优化呢?我们能不能让f[j]表示总体积小于等于j的取法中的最大价值呢?答案是肯定的。请看代码——
#include<iostream>
#include<cmath>
using namespace std;
const int K = 1010;int v[K],w[K],f[K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++) cin>>v[i]>>w[i];for(int i = 1;i<=N;i++)//这里省略了一行恒等式:f[j] = f[j]。这个式子的含义是,当j小于v[i]时,我们不能取第i个物品。//这里要从大到小遍历,是为了避免某个物品被重复取用。如图————for(int j = V;j>=v[i];j--)f[j] = max(f[j],f[j-v[i]]+w[i]);cout<<f[V]<<endl;return 0;
}
在计算f[2]时,我们可以发现物品1被放进去了两次,这是不被允许的。会产生这样结果的原因是j - v[i]<j,那么f[j-v[i]]在该第i轮循环中已经被计算过,也就是说f[j-v[i]]的真实含义是f[i][j-v[i]],它的值已经被“污染”。但是对比上一份二维数组的代码,我们知道我们要的其实是f[i-1][j-v[i]]。而若倒序遍历,j-v[i]<j,遍历到j-v[i]在j之后,也就是说第i轮循环时j-v[i]还没有计算到,代码会利用第i-1轮循环的值来代替,这正合我们的心意。
我们还可以优化输入,边输入边处理,这样就不用开额外的数组了。
#include<iostream>
#include<cmath>
using namespace std;const int K = 1010;
int f[K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w;cin>>v>>w;for(int j = V;j>=v;j--)f[j] = max(f[j],f[j-v]+w);}cout<<f[V]<<endl;
}
2.完全背包问题

我们仍然首先考虑朴素算法。像上一题一样,我们开一个f数组,其中f[i][j]表示在前i个物品中取且总体积不大于j的取法的最大价值。那么第i个物品可以取0,1,2,3……k个。第i个物品不能无限取,因为背包的容量是有限的。那么我们就有了递推式(这里kv[i]<=V且j-kv[i]>=0,因为j<=V,我们只需要让k*v[i]<=j)——
f[i][j] = max(f[i-1][j-0*v[i]]+0*w[i],f[i-1][j-1*v[i]]+1*w[i],……,f[i-1][j-k*v[i]]+k*w[i]);
代码如下——
#include<iostream>
#include<cmath>
using namespace std;const int K = 1001;
int f[K][K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w;cin>>v>>w;for(int j = 0;j<=V;j++){for(int k = 0;k*v<=j;k++)f[i][j] = max(f[i][j],f[i-1][j-k*v]+k*w);}}cout<<f[N][V]<<endl;return 0;
}
这样我们就用到了三层循环。但是这个方法在Acwing中是会爆TLE的,我们能不能通过观察减少循环次数呢?

因此我们的代码可以被优化为——
#include<iostream>
#include<cmath>
using namespace std;const int K = 1001;
int f[K][K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w;cin>>v>>w;for(int j = 0;j<=V;j++){if(j>=v) f[i][j] = max(f[i-1][j],f[i][j-v]+w);//别忘了考虑j<v,即放不下第i个物品的情形else f[i][j] = f[i-1][j];}}cout<<f[N][V]<<endl;return 0;
}
优化成一维数组如下:
#include<iostream>
#include<cmath>
using namespace std;const int K = 1001;
int f[K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w;cin>>v>>w;for(int j = v;j<=V;j++)//这里不需要倒序遍历,是因为我们要的本来就是f[i][j-v],就是在这一层被算过的.倒序反而会出错,因为j-v<j还没有在这一层被算过,因此会调用f[i-1][j-v],这不是我们想要的。f[j] = max(f[j],f[j-v]+w);}cout<<f[V]<<endl;return 0;
}
3.多重背包问题(朴素版)

#include<iostream>
using namespace std;const int K = 1010;
int f[K][K];int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w,s;cin>>v>>w>>s;for(int j = V;j>=0;j--)for(int k = 0;k*v<=j&&k<=s;k++)f[i][j] = max(f[i][j],f[i-1][j-k*v]+k*w);}cout<<f[N][V]<<endl;return 0;
}
4.多重背包问题(二进制优化版)

当我们尝试像3.一样对代码进行优化时,我们会发现一个问题,即f[i][j]不能直接由f[i][j-v]来表示。原因如下图(假设总体积不大于j时所有该物品都能被放进去)——

我们会发现,f[i][j-v[i]]会多出来一项导致不能完全对齐。那么为什么在完全背包问题中不会出现这种情况呢?因为那里的物品时无限个的,制约物品个数的是j而不是s,所以可以对齐。那么我们该如何进行优化呢?这里介绍二进制优化的神奇方法。它的基本思想是按照2的整数次幂将物品分为若干组,每组只有取和不取两种情况。这样就转化成了一个01背包问题。那么这样的分法是否可以囊括所有可能的选择呢?请看——

如果s是一般的数(不能被表示成2的幂乘的和)呢?

下面让我们一起来看看具体的代码实现吧!
#include<iostream>
#include<cmath>
using namespace std;
//由于log2(2000)*1000 = 11000,我们开到15000。
const int K = 15000;
//processed_v、processed_w分别表示打包后的体积和价值。
int f[K],processed_v[K],processed_w[K];
//cnt为计数器,表示当前的组数。
int cnt = 0;int main()
{int N,V;cin>>N>>V;for(int i = 1;i<=N;i++){int v,w,s;cin>>v>>w>>s;int k = 1;while(k<=s){cnt++;processed_v[cnt] = k*v;processed_w[cnt] = k*w;s-=k;k*=2;}//如果有剩下,也要打包if(s>0){cnt++;processed_v[cnt] = s*v;processed_w[cnt] = s*w;}}//对打包后的物品做01背包问题。for(int i = 1;i<=cnt;i++)for(int j = V;j>=processed_v[i];j--)f[j] = max(f[j],f[j-processed_v[i]]+processed_w[i]);cout<<f[V]<<endl;return 0;
}
5.分组背包问题

以上就是本篇文章的全部内容啦!如果你感觉有帮助,请多多支持博主!
相关文章:

XCPC第九站———背包问题!
1.01背包问题 我们首先定义一个二维数组f,其中f[i][j]表示在前i个物品中取且总体积不超过j的取法中的最大价值。那么我们如何得到f[i][j]呢?我们运用递推的思想。由于第i个物品只有选和不选两种情况,当不选第i个物品时,f[i][j]f[i…...

【软考 系统架构设计师】论文范文④ 论基于构件的软件开发
>>回到总目录<< 文章目录 论基于构件的软件开发范文摘要正文论基于构件的软件开发 软件系统的复杂性不断增长、软件人员的频繁流动和软件行业的激烈竞争迫使软件企业提高软件质量、积累和固化知识财富,并尽可能地缩短软件产品的开发周期。 集软件复用、分布式对…...

spring-integration-redis中分布式锁RedisLockRegistry的使用
pom依赖:<!-- redis --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId></dependency><dependency><groupId>org.springframework.integ…...
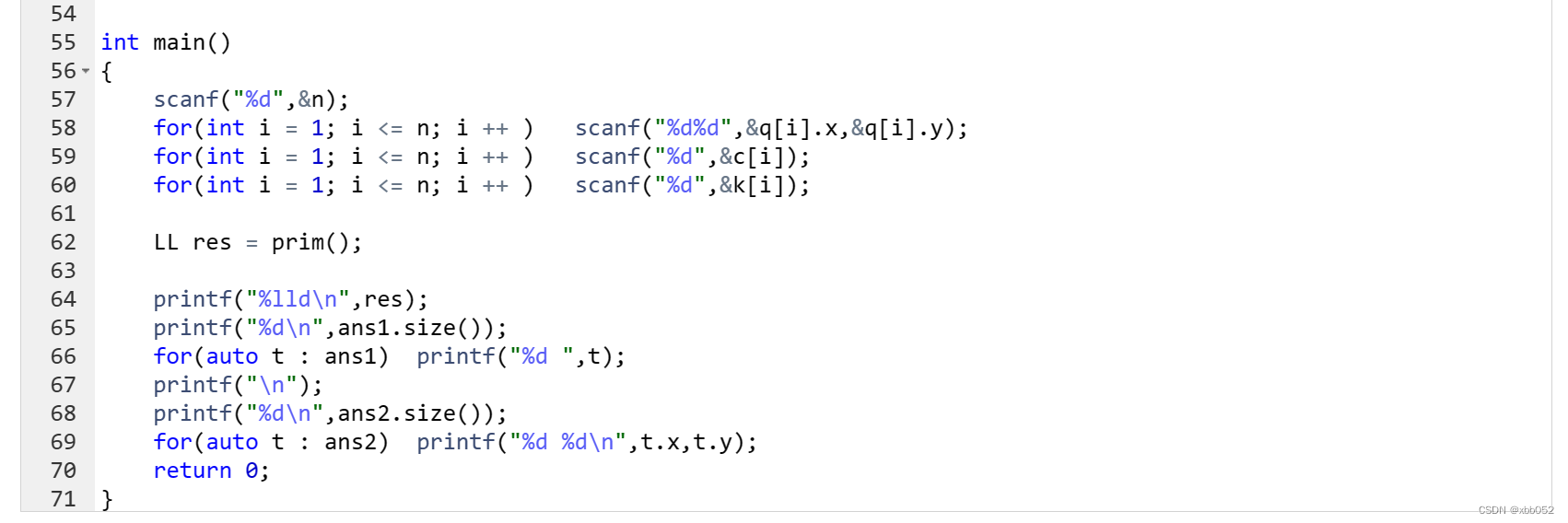
城市通电(prim算法)
acwing3728 蓝桥杯集训每日一题 平面上遍布着 n 座城市,编号 1∼n。 第 i 座城市的位置坐标为 (xi,yi) 不同城市的位置有可能重合。 现在要通过建立发电站和搭建电线的方式给每座城市都通电。 一个城市如果建有发电站,或者通过电线直接或间接的与建…...

【动态规划】
动态规划1引言题目509. 斐波那契数70. 爬楼梯746. 使用最小花费爬楼梯小结53. 最大子数组和结语引言 蓝桥杯快开始了啊,自从报名后还没认真学过算法有(>﹏<)′,临时抱一下佛脚,一起学学算法。 题目 509. 斐波那契数 斐波那契数 &am…...

秒懂算法 | DP概述和常见DP面试题
动态(DP)是一种算法技术,它将大问题分解为更简单的子问题,对整体问题的最优解决方案取决于子问题的最优解决方案。本篇内容介绍了DP的概念和基本操作;DP的设计、方程推导、记忆化编码、递推编码、滚动数组以及常见的DP面试题。 01、DP概述 1. DP问题的特征 下面以斐波那…...
)
【C++提高编程】C++全栈体系(二十五)
C提高编程 第四章 STL- 函数对象 一、函数对象 1. 函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象函数对象使用重载的()时,行为类似函数调用,也叫仿函数 本质: 函数对象(仿函数)是一个类&…...

【云原生】k8s核心技术—集群安全机制 Ingress Helm 持久化存储-20230222
文章目录一、k8s集群安全机制1. 概述2. RBAC——基于角色的访问控制二、Ingress三、Helm1. 引入2. 使用功能Helm可以解决哪些问题3. 介绍4. 3个重要概念5. helm 版本变化6. helm安装及配置仓库7. 使用helm快速部署应用8. 自己创建chart9. 实现yaml高效复用四、持久化存储1.nfs—…...
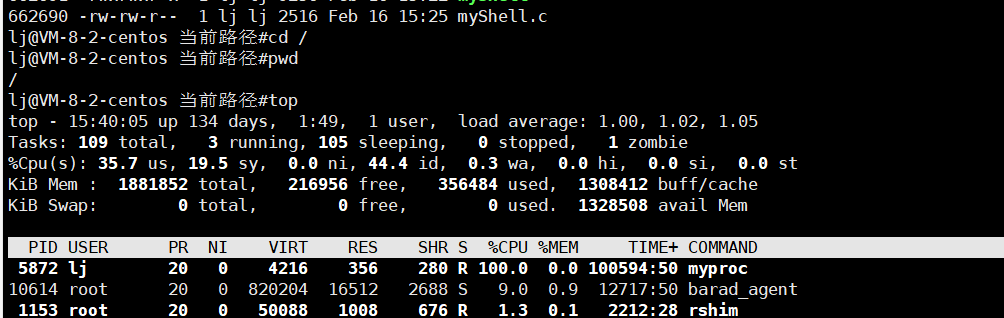
【Linux】实现简易的Shell命令行解释器
大家好我是沐曦希💕 文章目录一、前言二、准备工作1.输出提示符2.输入和获取命令3.shell运行原理4.内建命令5.替换三、整体代码一、前言 前面学到了进程创建,进程终止,进程等待,进程替换,那么通过这些来制作一个简易的…...

再获认可!腾讯安全NDR获Forrester权威推荐
近日,国际权威研究机构Forrester发布最新研究报告《The Network Analysis And Visibility Landscape, Q1 2023》(以下简称“NAV报告”),从网络分析和可视化(NAV)厂商规模、产品功能、市场占有率及重点案例等…...
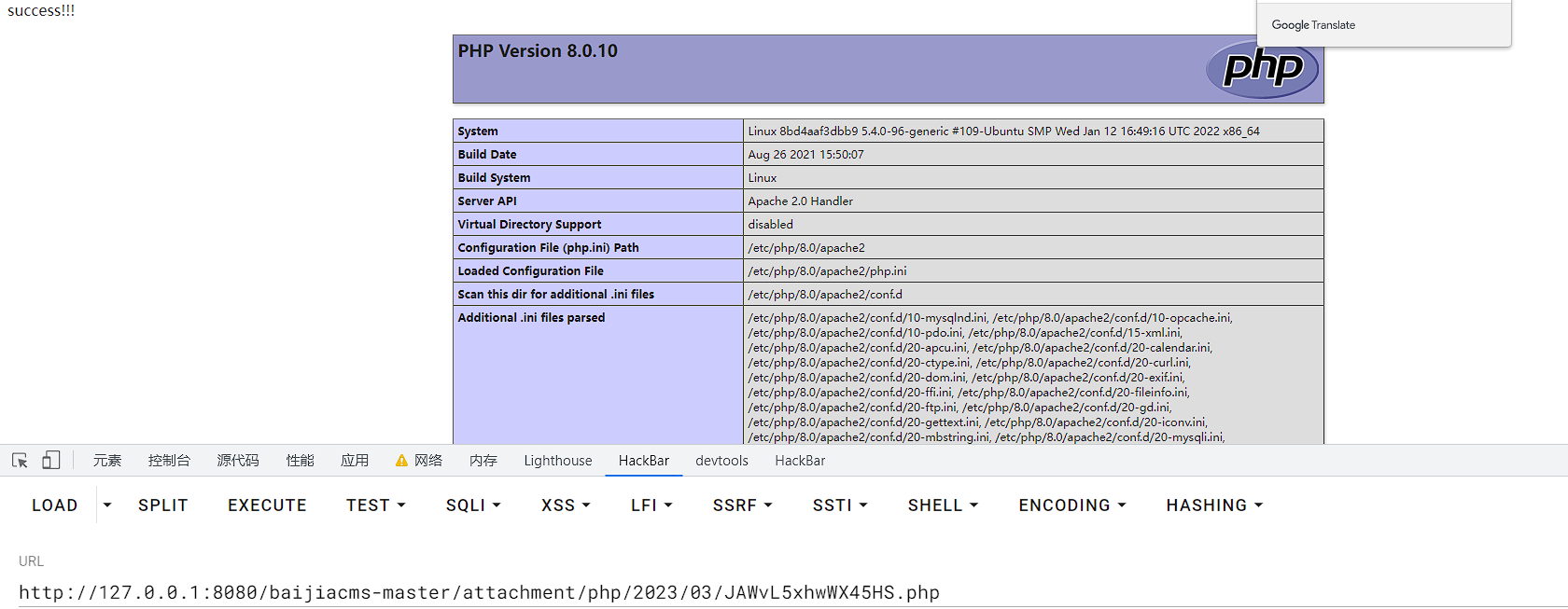
代码审计之旅之百家CMS
前言 之前审计的CMS大多是利用工具,即Seay昆仑镜联动扫描出漏洞点,而后进行审计。感觉自己的能力仍与零无异,因此本次审计CMS绝大多数使用手动探测,即通过搜索危险函数的方式进行漏洞寻找,以此来提升审计能力…...
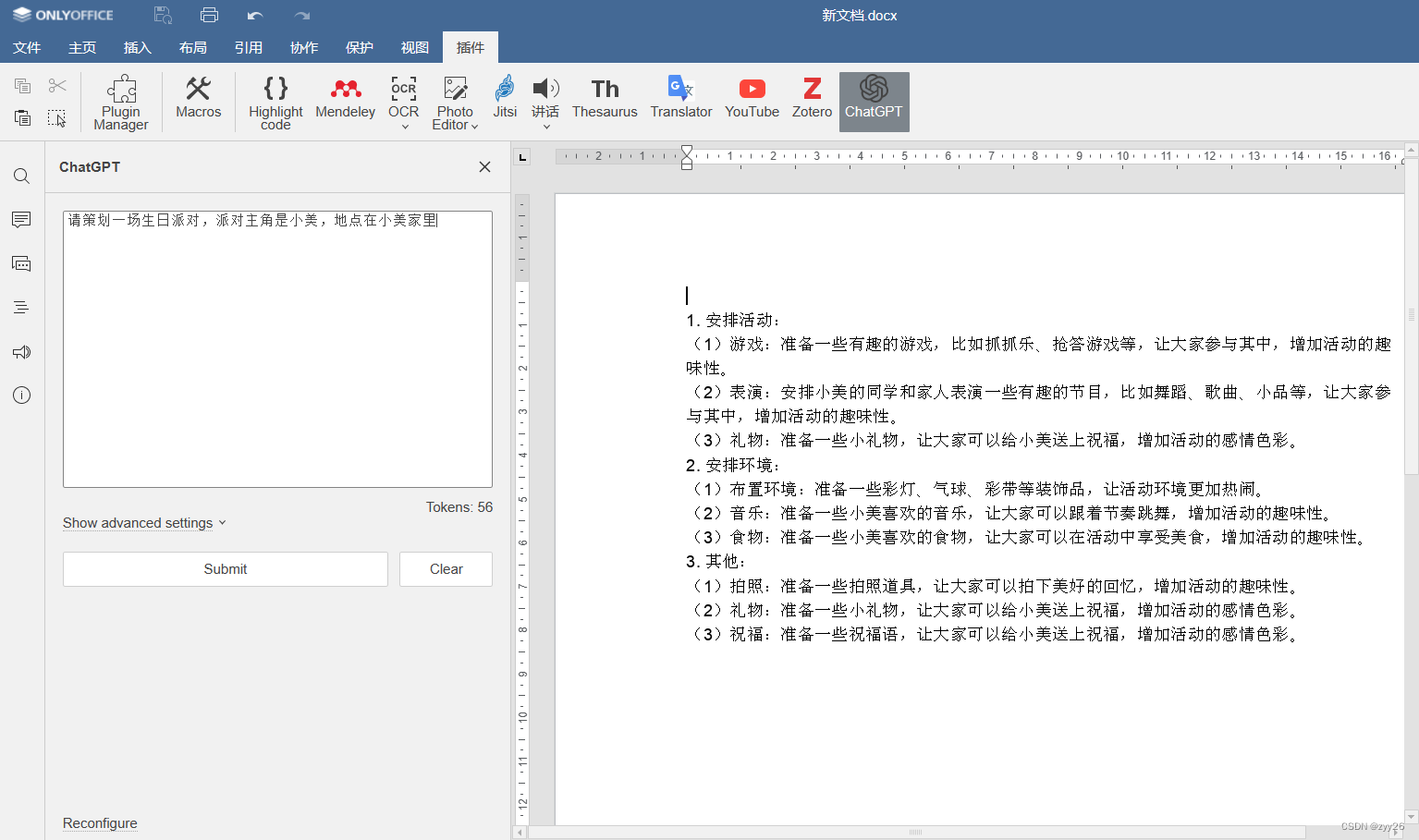
ONLYOFFICE中利用chatGPT帮助我们策划一场生日派对
近日,人工智能chatGPT聊天机器人爆火,在去年年底发布后,仅仅两个月就吸引了全球近一亿的用户,成为史上最快的应用消费程序,chatGPT拥有强大的学习和交互能力 可以被学生,教师,上班族各种职业运…...
)
Java面试题-线程(一)
在典型的 Java 面试中, 面试官会从线程的基本概念问起, 如:为什么你需要使用线程,如何创建线程,用什么方式创建线程比较好(比如:继承 thread 类还是调用 Runnable 接口),…...

一篇普通的bug日志——bug的尽头是next吗?
文章目录[bug 1] TypeError: method object is not subscriptable[bug 2] TypeError: unsupported format string passed to numpy.ndarray.__format__[bug 3] ValueError:Hint: Expected dtype() paddle::experimental::CppTypeToDataType<T>::Type()[bug 4] CondaSSLE…...

Vue 3 第八章:Watch侦听器
文章目录Watch侦听器1. 基础概念1.1. Watch的基本用法例子1:监听单个ref的值,直接监听例子2:监听多个ref的值,采用数组形式例子3:深度监听例子4:监听reactive响应式对象单一属性,采用回调函数的…...
GlassFish的安装与使用
一、产品下载与安装glassfish下载地址:https://download.oracle.com/glassfish/5.0.1/release/index.html下载后解压即完成安装,主要目录说明:bin目录:为asadmin命令所在目录。glassfish为主目录:glassfish\bin目录为命…...
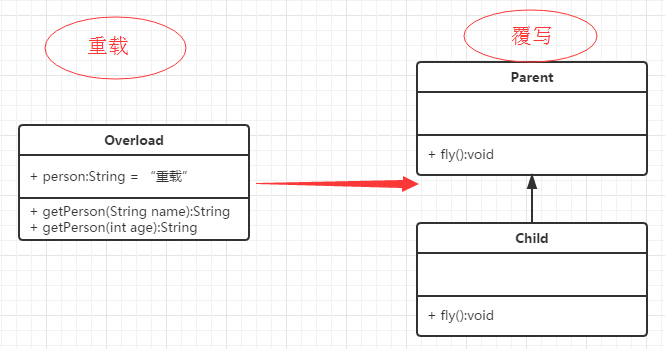
【java】Java 重写(Override)与重载(Overload)
文章目录重写(Override)方法的重写规则Super 关键字的使用重载(Overload)重载规则实例重写与重载之间的区别总结重写(Override) 重写是子类对父类的允许访问的方法的实现过程进行重新编写, 返回值和形参都不能改变。即外壳不变,核心重写! 重写的好处在于…...
OpenCV-PyQT项目实战(12)项目案例08:多线程视频播放
欢迎关注『OpenCV-PyQT项目实战 Youcans』系列,持续更新中 OpenCV-PyQT项目实战(1)安装与环境配置 OpenCV-PyQT项目实战(2)QtDesigner 和 PyUIC 快速入门 OpenCV-PyQT项目实战(3)信号与槽机制 …...
面向对象设计模式:结构型模式之装饰器模式
文章目录一、引入二、装饰器模式2.1 Intent 意图2.2 Applicability 适用性2.3 类图2.4 优缺点2.5 应用实例:Java IO 类2.6 应用实例:咖啡馆订购系统一、引入 咖啡馆订购系统 Initial 初始 4 种咖啡 House blend (混合咖啡)Dark Roast (深度烘培)Decaf (…...
Unity iOS 无服务器做一个排行榜 GameCenter
排行榜需求解决方案一(嗯目前只有一)UnityEngine.SocialPlatformsiOS GameCenterAppStoreConnect配置Unity 调用(如果使用GameCenter系统的面板,看到这里就可以了)坑(需要获取数据做自定义面板的看这里)iOS代码Unity 代码吐槽需求 需求:接入…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
