【小程序】生成短信中可点击的链接
文章目录
- 前言
- 一、如何生成链接
- 二、仔细拜读小程序开发文档
- 文档说明1
- 文档说明2
- 总结
前言
由于线上运营需求,需要给用户发送炮轰短信,用户通过短信点击链接直接跳转进入小程序
一、如何生成链接
先是找了一些三方的,生成的倒是快速,但是需要给提供appid和appkey啥的,不太安全。而且点的多了还要收费。。。作为一个开发,用三方的多少有点儿耻辱了。
二、仔细拜读小程序开发文档
第一个想到的是小程序的短链。
文档说明1
Short Link

好像是这个东西,继续往下看

啊哦,我们的小程序不是电商类的,直接pass掉了。而且这里是提供在微信内拉起的。
文档说明2
generateUrl


哦,原来我们的是这个的,这里写了短信可以拉起小程序。那就试一下吧

点击这个调试工具
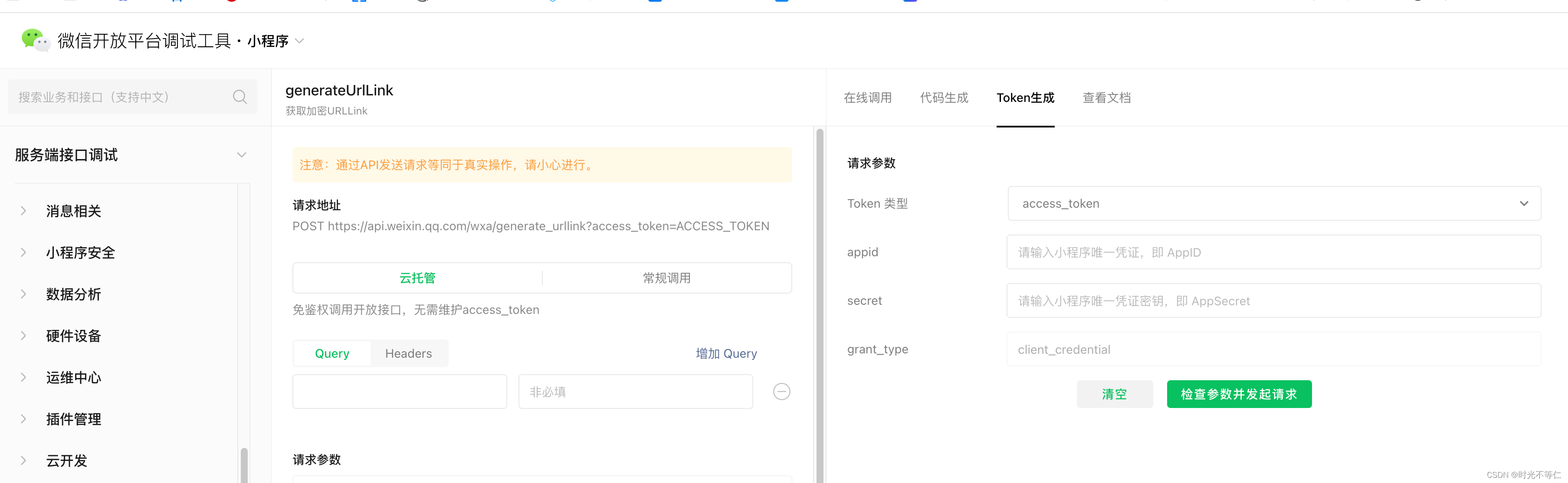
工具里可以现生成一个token,也可以自己是开发的话,正常redis里会存这个token的。直接拿来用。
然后就可以调用
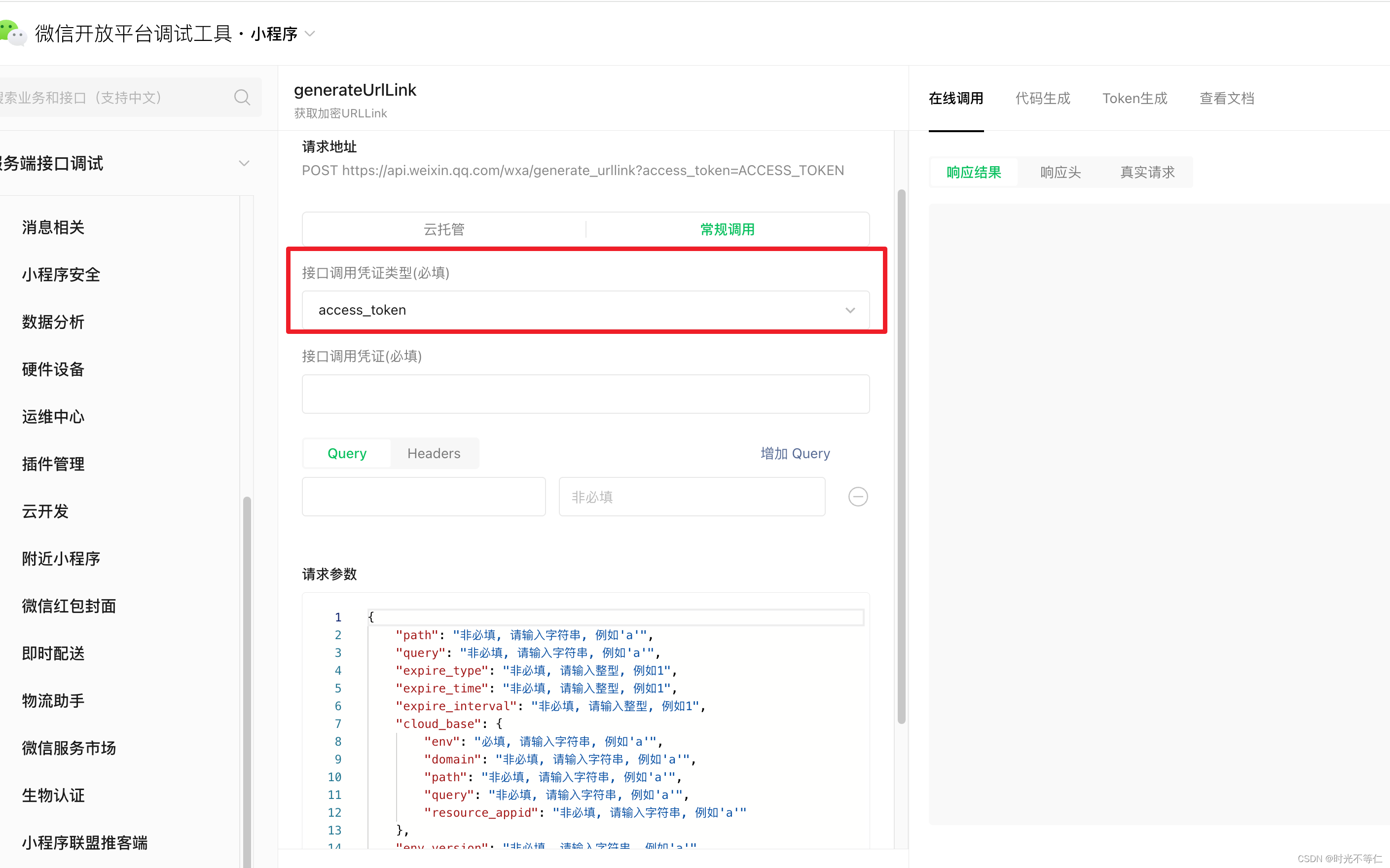
这里选择使用access_token的方式获取,然后下边填写参数
path如果不指定,则默认跳转到首页,填写了有效的地址,这个需要找前端开发人员要这个指定页面的路径,可以去小程序开发工具里查到,然后就可以参考具体的其他参数进行生成一个短信跳转的链接了。
总结
以前对腾讯文档的印象是很看不好,没啥用的感觉,没想到这个文档这么给力。
相关文章:

【小程序】生成短信中可点击的链接
文章目录 前言一、如何生成链接二、仔细拜读小程序开发文档文档说明1文档说明2 总结 前言 由于线上运营需求,需要给用户发送炮轰短信,用户通过短信点击链接直接跳转进入小程序 一、如何生成链接 先是找了一些三方的,生成的倒是快速…...

欧拉函数(模板题)
给定 n 个正整数 ai,请你求出每个数的欧拉函数。 欧拉函数的定义 输入格式 第一行包含整数 n。 接下来 n 行,每行包含一个正整数 ai。 输出格式 输出共 n 行,每行输出一个正整数 ai 的欧拉函数。 数据范围 1≤n≤100, 1≤ai≤2109 输…...
Thingsboard PE 白标的使用
只有专业版支持白标功能。 使用 ThingsBoard Cloud 或安装您自己的平台实例。 一、介绍 ThingsBoard Web 界面提供了简便的操作,让您能够轻松配置您的公司或产品标识和配色方案,无需进行编码工作或重新启动服务。 系统管理员、租户和客户管理员可以根据需要自定义配色方案、…...

智能物联网远传冷水表管理系统
智能物联网远传冷水表管理系统是一种基于物联网技术的先进系统,旨在实现对冷水表的远程监测、数据传输和智能化管理。本文将从系统特点、构成以及带来的效益三个方面展开介绍。 系统特点 1.远程监测:系统可以实现对冷水表数据的远程监测,无…...
Qt教程3-Ubuntu(x86_64)上配置arm64(aarch64)交叉编译环境及QT编译arm64架构工程
汇创慧玩 写在前面1. 查看系统架构相关指令2. ARM64交叉编译器环境搭建3. Qt编译arm64环境搭建4. 配置 Qt的本地aarch64交叉编译器5. 工程建立及编译验证 写在前面 苦辣酸甜时光八载,春夏秋冬志此一生 Qt简介: Qt(官方发音 [kju:t]ÿ…...
-Python-OD统一考试(C卷))
2024年华为OD机试真题-最长子字符串的长度(二)-Python-OD统一考试(C卷)
题目描述: 给你一个字符串 s,字符串s首尾相连成一个环形 ,请你在环中找出l、o、x 字符都恰好出现了偶数次最长子字符串的长度。 输入描述: 输入是一串小写的字母组成的字符串。 输出描述: 输出是一个整数 补充说明: 1 <= s.length <= 5 x 10^5 s 只包含小写英文字母…...

【24届数字IC秋招总结】正式批面试经验汇总5——蔚来、tp-link
文章目录 一、蔚来-数字芯片验证工程师1.1 一面面试问题1.2 二面面试问题二、tp-link-数字IC验证工程师2.1 面试问题一、蔚来-数字芯片验证工程师 面试时间:9.6 10.6 1.1 一面面试问题 1、 讲下项目结构 2、 scoreboard如何进行数据对比的 3、 golden 数据怎么产生的 4、 在…...
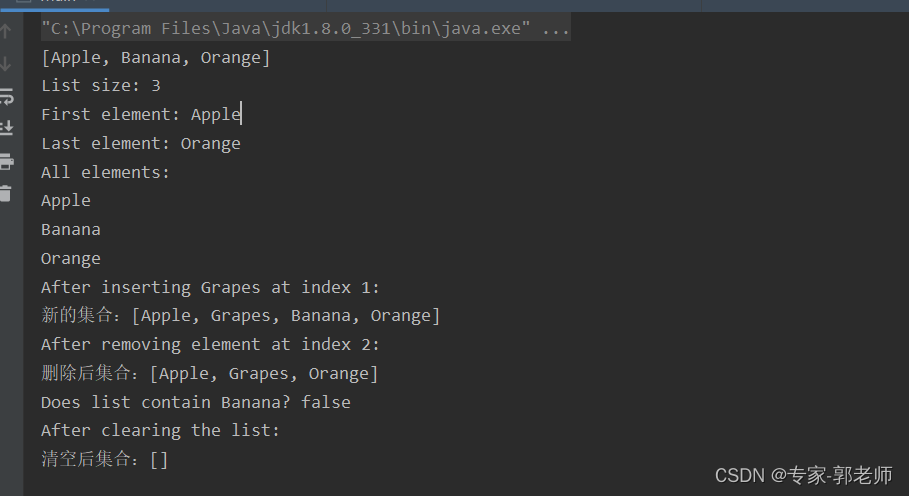
【JAVA基础篇教学】第八篇:Java中List详解说明
博主打算从0-1讲解下java基础教学,今天教学第八篇:Java中List详解说明。 在 Java 编程中,List 接口是一个非常常用的集合接口,它代表了一个有序的集合,可以包含重复的元素。List 接口提供了一系列操作方法,…...
RN向上向下滑动组件封装(带有渐变色)
这段组件代码逻辑是出事有一个View和下面的块,下面的块也就是红色区域可以按住向上向下滑动,当滑动到屏幕最上面则停止滑动,再向上滑动的过程中,上方的View的背景色也会有个渐变效果,大概逻辑就是这样 代码如下 import React, {useEffect, useRef, useState} from react; impo…...
)
27、Lua 学习笔记之五(Lua中的数学库)
Lua中的数学库 Lua5.1中数学库的所有函数如下表: math.pi 为圆周率常量 3.14159265358979323846 数学库说明例子方法abs取绝对值math.abs(-15)15acos反余弦函数math.acos(0.5)1.04719755asin反正弦函数math.asin(0.5)0.52359877atan2x / y的反正切值math.atan2(9…...

【C++成长记】C++入门 | 类和对象(中) |拷贝构造函数、赋值运算符重载、const成员函数、 取地址及const取地址操作符重载
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:C❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、拷贝构造函数 1、概念 2、特征 二、赋值运算符重载 1、运算符重载 2、赋值运算符重载 3、前置…...

OpenHarmony实战开发-页面深色模式适配。
介绍 本示例介绍在开发应用以适应深色模式时,对于深色和浅色模式的适配方案,采取了多种策略如下: 1. 固定属性适配:对于部分组件的颜色属性,如背景色或字体颜色,若保持不变,可直接设定固定色值…...
域名解析出现错误,该如何解决?
域名作为网络地址,是我们访问网站的必经之路,域名解析就是把你的域名解析成一个ip地址,在使用的过程中遇到域名解析文件异常也是常有的事。如果域名解析出现错误,该怎么解决呢? 一、打开网页时,显示域名解析…...
从iPhone恢复已删除照片的最佳软件
本文分享了从iPhone恢复已删除照片的最佳软件。如果您正在寻找如何从iPhone恢复已删除的照片,请查看这篇文章。 为什么您需要软件从iPhone恢复已删除的照片? 没有什么比丢失iPhone上的重要数据更痛苦的了,尤其是一些具有珍贵回忆的照片。有时…...
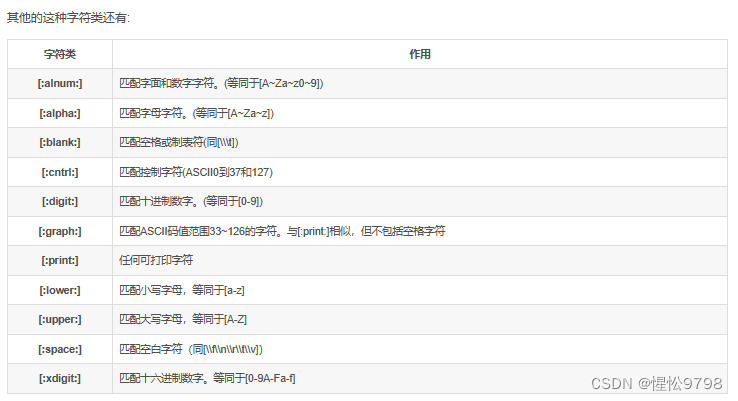
MySQL模糊查询
一、MySQL通配符模糊查询(%,_) 1.1.通配符的分类 1.“%”百分号通配符:表示任何字符出现任意次数(可以是0次) 2.“_”下划线通配符:表示只能匹配单个字符,不能多也不能少,就是一个字符。当然…...

QEMU_v8搭建OP-TEE运行环境
文章目录 一、依赖下载二、设置网络三、安装下载四、运行OP-TEE 一、依赖下载 更新依赖包,下载一系列依赖。比如Python需要Python3.x版本,需要配置git的用户名和邮箱等。这里不详细展开了,很多博客都有涉及到。 二、设置网络 这一点非常重…...
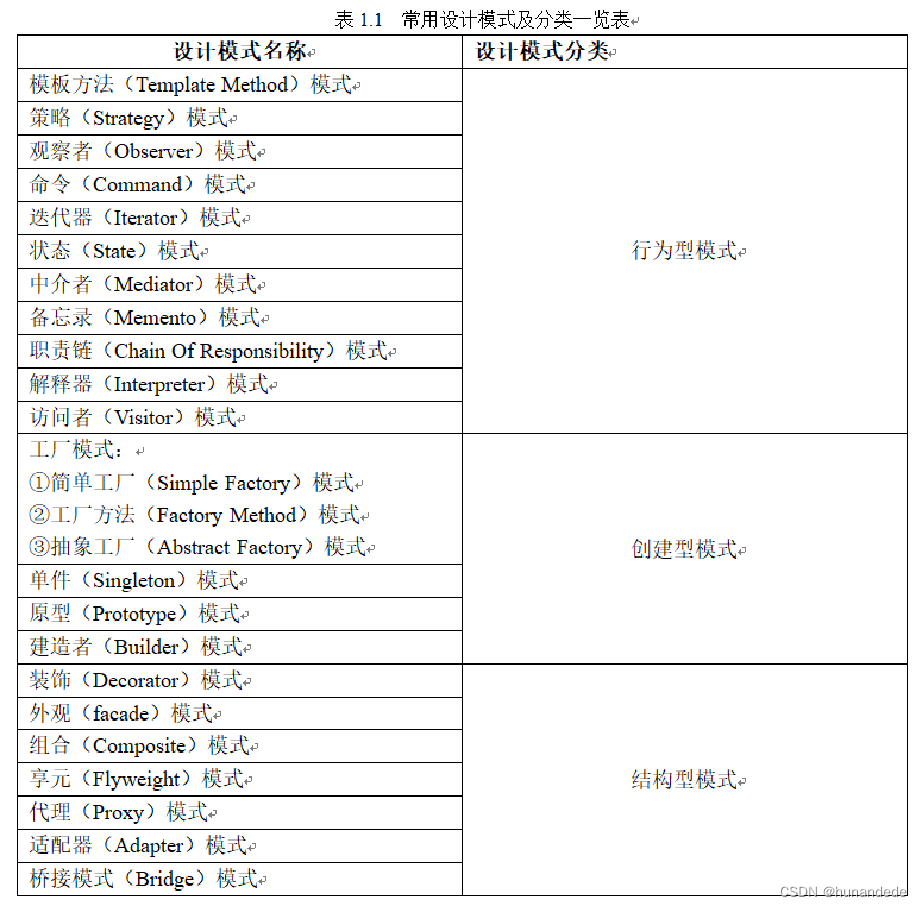
C++11 设计模式0. 设计模式的基本概念,设计模式的准则,如何学习设计模式,24种设计模式的分为3大类
一 设计模式的基本概念: 模式:指事物的标准样式 或者 理解成 针对特定问题的可重用解决方案。 设计模式,是在特定问题发生时的可重用解决方案。 设计模式一般用于大型项目中。 大型项目中,设计模式保证所设计的模块之间代码的灵…...
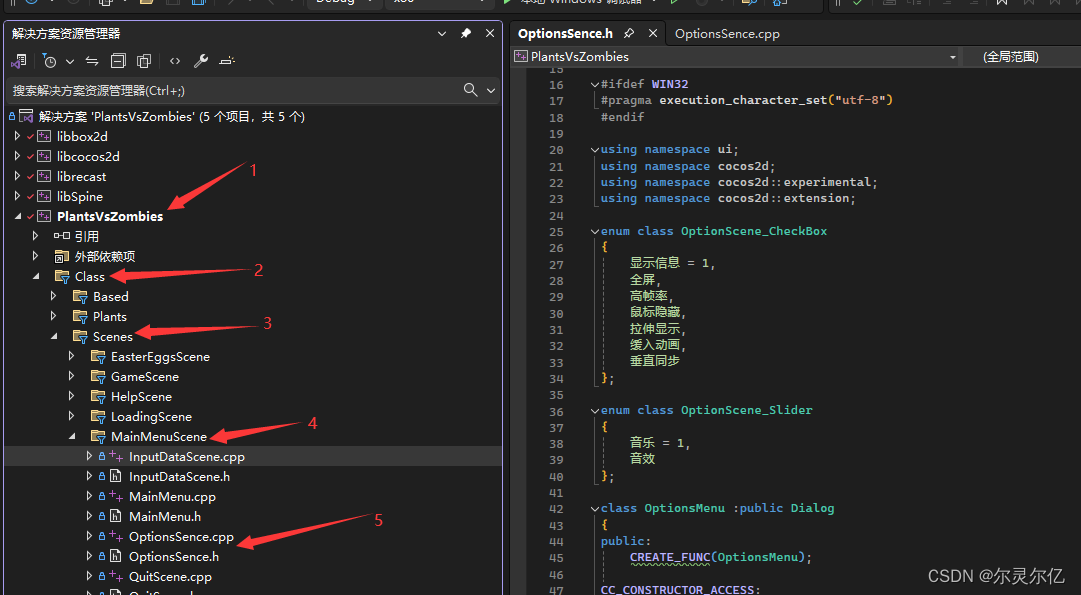
(十)C++自制植物大战僵尸游戏设置功能实现
植物大战僵尸游戏开发教程专栏地址http://t.csdnimg.cn/m0EtD 游戏设置 游戏设置功能是一个允许玩家根据个人喜好和设备性能来调整游戏各项参数的重要工具。游戏设置功能是为了让玩家能够根据自己的需求和设备性能来调整游戏,以获得最佳的游戏体验。不同的游戏和平…...
)
数据结构——通讯录(顺序表的实战项目)
(—).通讯录的功能 大家应该都十分了解通讯录的功能吧,无非就是对联系人的增添删除,还有信息的修改,并且联系人信息要包含名字,电话,性别,地址等。我把通讯录的功能总结如下&#x…...
)
数据库-Redis(14)
目录 66.Redis为什么主从全量复制使用RDB而不是使用AOF? 67.Redis为什么还有无磁盘复制模式? 68.Redis为什么还会有从库的从库设计?...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
