AdaBoost 算法
目录
什么是 AdaBoost 算法?
Adaboost 的 7 个优缺点
集成学习:人多力量大:
- Bagging:民主。
- Boosting :挑选精英。
长短期记忆网络:引入遗忘机制
生成对抗网络 :物竞天择适者生存
首先,了解一下集成学习及 Boosting 算法
集成学习归属于机器学习,他是一种「训练思路」,并不是某种具体的方法或者算法。
现实生活中,大家都知道「人多力量大」,「3 个臭皮匠顶个诸葛亮」。而集成学习的核心思路就是「人多力量大」,它并没有创造出新的算法,而是把已有的算法进行结合,从而得到更好的效果。
集成学习会挑选一些简单的基础模型进行组装,组装这些基础模型的思路主要有 2 种方法:
- bagging(bootstrap aggregating的缩写,也称作“套袋法”)
- boosting <
相关文章:

AdaBoost 算法
目录 什么是 AdaBoost 算法? Adaboost 的 7 个优缺点 集成学习:人多力量大: Bagging:民主。Boosting :挑选精英。长短期记忆网络:引入遗忘机制 生成对抗网络 :物竞天择适者生存 首先,了解一下集成学习及 Boosting 算法 集成学习归属于机器学习,他是一种「训练思路…...

链接分析算法
链接分析(Link Analysis)通常指的是对图(Graph)中的节点(Nodes)和边(Edges)进行分析,以发现图的结构和属性。在图论中,链接分析算法通常用于解决诸如网页排名…...

怎么批量完成图片格式转换?介绍三种简单方法
在日常生活和工作中,我们经常会遇到需要将图片格式转换的情况,无论是为了适应不同的设备要求,还是为了能让我们的图片应用到更多的使用场景中去,批量图片格式转换都是一项非常实用的技能。本文将介绍一些常见的批量图片格式转换方…...
每日OJ题_BFS解决最短路③_力扣127. 单词接龙
目录 ③力扣127. 单词接龙 解析代码 ③力扣127. 单词接龙 127. 单词接龙 难度 困难 字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk: 每一对相邻的单词只差一个字母。…...
微信小程序英文版:实现一键切换中英双语版(已组件化)
已经重新优化代码做成了组件,需要可自取:https://github.com/CrystalCAI11/wechat-language-compoment 所有操作都打包在组件里不需要在额外的地方添加代码,直接在你需要的页面里导入组件,再在对应页面的onLoad()里set文本就行了。…...

openstack之neutron介绍
核心组件 neutron-server:提供API接口,把对应的api请求传给plugin进; neutron-plugin:管理逻辑网络状态,调用agent; neutron-agent:在provider network上创建网络对象; neutron-…...

学习Rust的第三天:猜谜游戏
基于Steve Klabnik的《The Rust Programming Language》一书。今天我们在rust中建立一个猜谜游戏。 Introduction 介绍 We will build a game that will pick a random number between 1 to 100 and the user has to guess the number on a correct guess the user wins. 我们将…...

React中子传父的方式及原理
方式挺多的,先说最常用的通过props进行父子组件的数据传递和修改以及原理 在React中,props不仅用于传递数据,它们也可以传递可以执行的函数,这使得子组件能够间接更新父组件的状态。这种方法强化了React的单向数据流策略…...
【数据结构与算法】贪心算法及例题
目录 贪心算法例题一:找零问题例题二:走廊搬运物品最优方案问题输入样例例题三:贪心自助餐 贪心算法 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,以期望最终达到全局最优解的算法。它的核心思想是每次都选择当前最…...
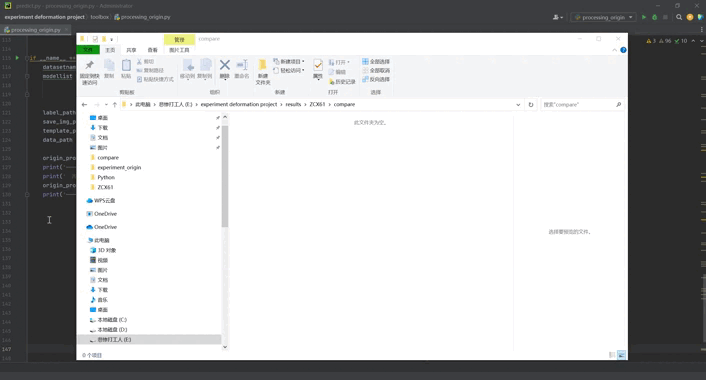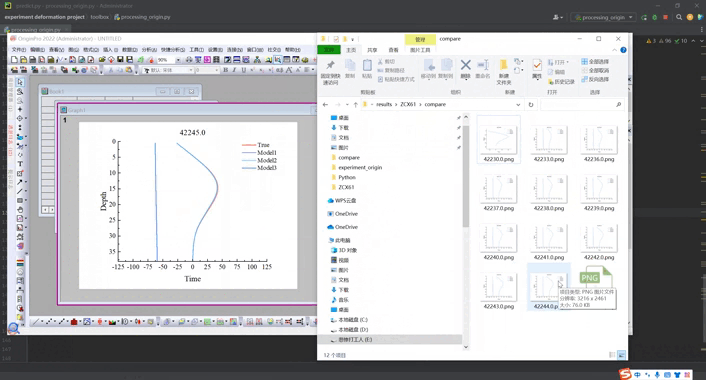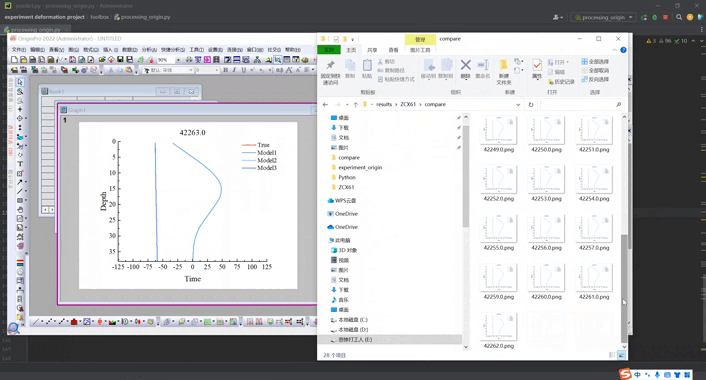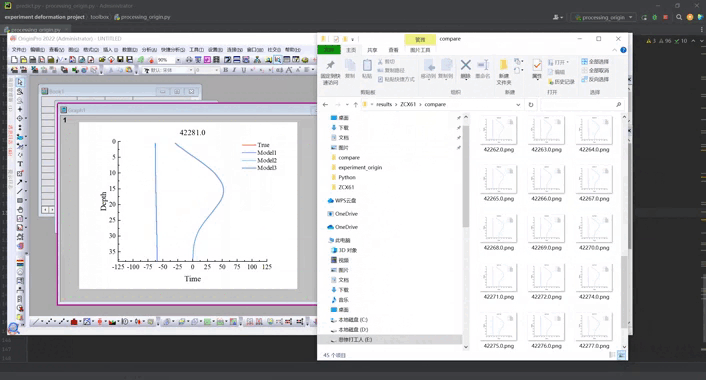
【Origin+Python】使用External Python批量出图代码参考
目录 基本介绍环境配置官方代码示例基础代码详解我的代码效果视频进阶代码及去水印 基本介绍 origin2021后可以使用python实现批量绘图,一共有两种方式:一种是嵌入式Python,一种是外部Python访问Origin。详细介绍可以自己去查看,打…...
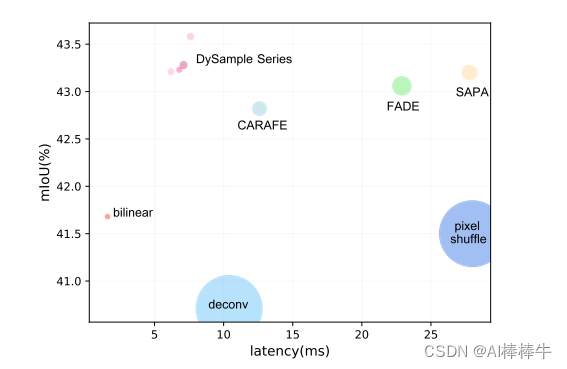
YOLOv8最新改进系列:融合DySample超轻量动态上采样算子,低延迟、高性能,目前最新上采样方法!!!遥遥领先!
YOLOv8最新改进系列:融合DySample超轻量动态上采样算子,低延迟、高性能,目前最新上采样方法!!!遥遥领先! DySample超轻量动态上采样算子全文戳这!here! 详细的改进教程以及源码&am…...

ChatGPT基础(二) ChatGPT的使用和调优
文章目录 ChatGPT的特性采用关键词进行提问给ChatGPT指定身份提升问答质量的策略1.表述方式上的优化2.用"继续"输出长内容3.营造场景4.由浅入深,提升问题质量5.预设回答框架和风格 ChatGPT的特性 1.能够联系上下文进行回答 ChatGPT回答问题是有上下文的&…...
麒麟 V10 离线 安装 k8s 和kuboard
目录 安装文件准备 主机准备 主机配置 修改主机名(三个节点分别执行) 配置hosts(所有节点) 关闭防火墙、selinux、swap、dnsmasq(所有节点) 安装依赖包(所有节点) 系统参数设置(所有节点) 时间同步…...

PlayerSettings.WebGL.emscriptenArgs设置无效的问题
1)PlayerSettings.WebGL.emscriptenArgs设置无效的问题 2)多个小资源包合并为大资源包的疑问 3)AssetBundle在移动设备上丢失 4)Unity云渲染插件RenderStreaming,如何实现多用户分别有独立的操作 这是第381篇UWA技术知…...
项目管理工具——使用甘特图制定项目计划的详细步骤
甘特图是一种直观的项目管理工具,它有助于我们清晰地展示任务安排、时间管理和项目的进度。以下是使用甘特图制定项目计划的详细步骤: 1、创建项目:首先,在进度猫中创建新的项目,并设置项目的时间、工作日等参数。根据…...

python读取文件数据写入到数据库中,并反向从数据库读取保存到本地
学python,操作数据库是必不可少的,不光要会写python代码,还要会写SQL语句,本篇文章主要讲如何把本地txt文件中的数据读取出来并写入到对应的数据库中,同时将数据库单个表中的数据读出来保存在本地txt文件中。 话不多说…...
社交媒体数据恢复:Viber
Viber是一款流行的即时通讯应用,用于发送消息、语音通话和视频通话。然而,有时候我们会不小心删除一些重要的Viber聊天记录,这时候就需要进行数据恢复。本文将介绍如何在安卓设备上进行Viber数据恢复。 一、使用安卓数据恢复软件 安卓数据恢…...

蓝桥杯赛事介绍
蓝桥杯是由工业和信息化部人才交流中心主办的全国性IT学科赛事,全称为“蓝桥杯全国软件和信息技术专业人才大赛”。该赛事旨在推动软件和信息领域专业技术人才培养,提升大学生的创新能力和就业竞争力,为行业输送具有创新能力和实践能力的高端…...
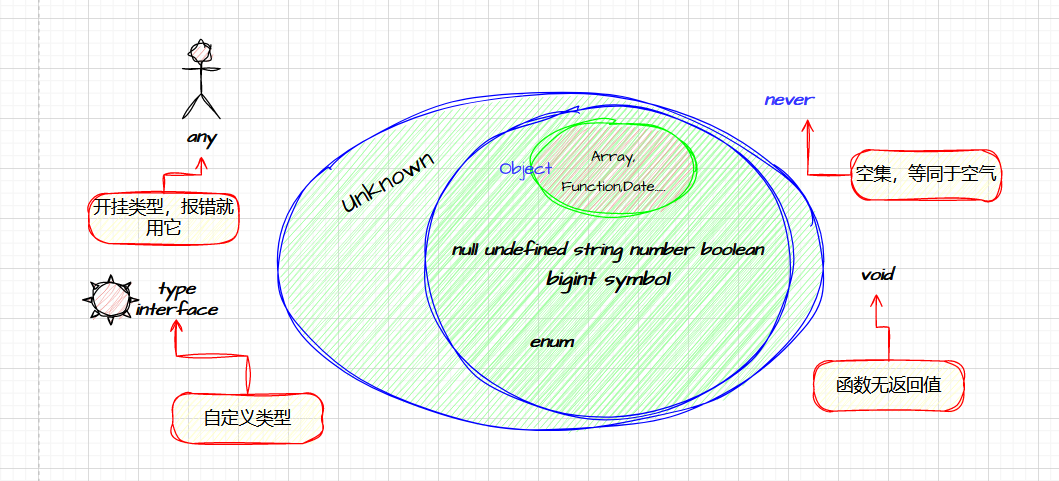
TypeScript系列之-深度理解基本类型画图讲解
JS的类型(8): null undefined string number boolean bigint symbol object(含 Array, Function,Date.....) TS的类型(87): 以上所有,加上 void, never, enum, unknown, any 再加上自定义类型 type interface 上一节我们说…...
Debian
使用root用户操作 直接使用su命令进行切换。 配置用户使用sudo命令 在安装好系统之后,使用用户名登录之后。需要执行需要root权限的命令,会发现无法执行成功。原因是没有配置用户使用sudo的权限。 编辑bash /etc/sudoers文件 可以先切换root用户安装…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
