堆放砖块-第12届蓝桥杯选拔赛Python真题精选

[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第47讲。
堆放砖块,本题是2021年1月23日举办的第12届蓝桥杯青少组Python编程选拔赛真题,题目要求编程计算按照一定规律进行堆放砖块的总数量。
先来看看题目的要求吧。
一.题目说明
提示信息:
有一堆砖,需要按照一定规律进行堆放,具体堆放规律如下:
顶层放1块砖,
第二层放3块砖,
第三层放6块砖,
第四层放10块砖,
......
依此类推,每一层砖块的数量为上一层砖块数量加上本层的层数。例如第五层为10 + 5 = 15。
输入砖块堆放的总层数,按照以上规律,求出砖块的总数。
编程实现:
输入砖块堆放的总层数,按照以上堆放规律,求出砖块的总数。
例如:输入为3,总层数为3层的砖块堆放一共有1 + 3 + 6 = 10块砖,则输出10。
输入描述:
输入一个正整数N(2 < N < 1000)作为砖块堆放的总层数
输出描述:
输出砖块的总数
样例输入:
3
样例输出:
10
二.思路分析
这是一道简单的计算题,考查的知识点主要是循环和变量。
古希腊毕达哥拉斯学派提出“万物皆数”,他们很重视数学,企图用数来解释一切。公元前6世纪,毕达哥拉斯学派在研究数的概念时,常常把数描绘成沙滩上的小石子,用它们进行各式各样的排列和分类,叫做“形数”。
他们发现数目为1,3,6,10,15,21……这些数量的石子,都可以排成三角形,像这样的数称为三角形数。
例如,前4个三角形数可以排成如下三角形:
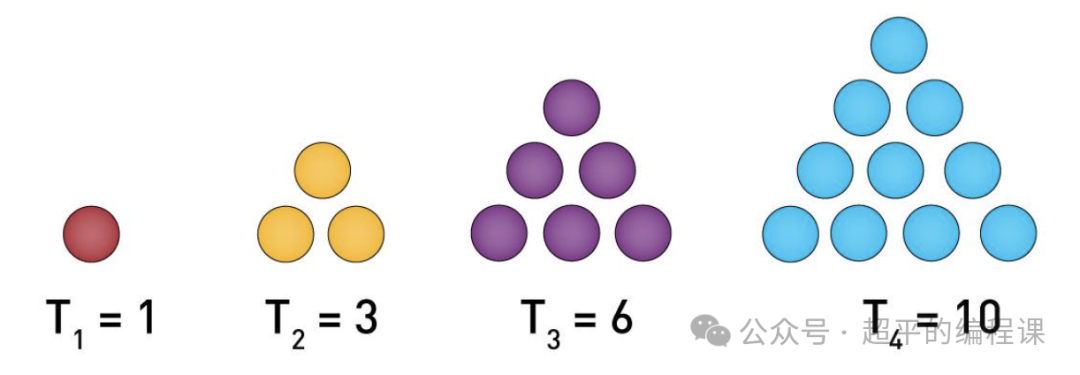
题目中的堆放砖块规律和三角形数完全一样,我们需要分析数字的增长规律,分析过程如下:
T2 - T1 = 3 - 1 = 2T3 - T2 = 6 - 3 = 3T4 - T3 = 10 - 6 = 4T5 - T4 = 15 - 10 = 5......
不难发现,前后两项的差是一个自然数列,在数学中这种数列被称作二级等差数列,或者差等差数列。
对于二级等差数列问题,典型的思路就是设置一个变量表示公差,在循环过程中不断地改变公差,这样就可以计算出每一项的值。
思路有了,接下来,我们就进入具体的编程实现环节。
三.编程实现
根据上面的思路分析,我们编写程序如下:

代码不多,强调两点:
1). 这里的a表示当前层的砖块数量,d表示公差,s表示总和,循环时,首先将当前层的砖块a进行累加,然后增加公差,再计算出下一层的砖块数量;
2). 由于第2层和第1层相差为2,所以将公差d的初始值设为1,并在循环中先将公差加1,再计算砖块数量,当然你也可以设置为不同的初始值和顺序,只要确保公差从2开始增加即可。
至此,整个程序就全部完成了,你也可以输入不同的层数来测试效果。
四.总结与思考
本题代码在10行左右,涉及到的知识点包括:
-
循环语句,主要for...in循环;
-
输入输出;
-
变量的使用;
本题难度一般,属于典型的循环累加题目。关键在于如何找到砖块递增的规律,从而计算出每一层的砖块数量,然后进行累加。
在实际比赛时,很多同学会遇到两个小麻烦,一是找不到砖块增加的规律,二是找到了规律,但不知道如何计算每一层的砖块。
针对对一个问题,说明平时在数学课上练习得不够。实际上,在小学二、三年级的课本中,有大量的数列找规律题目,比较典型的有等差数列、等比数列和斐波那契数列。
对于第二个问题,还是要灵活运用计算思维中的拆分思想,将复杂问题分解成多个简单的问题。由于每一层的砖块数量不能直接得出,不妨使用变量表示,先计算出每一层的砖块数量,然后考虑累加问题,如此一来,问题就变简单了。
超平老师给你留一道思考题,除了三角形数,你还知道有哪些其它形数吗,它们又有什么样的特点呢?
你还有什么好的想法和创意吗,也非常欢迎和超平老师分享探讨。
如果你觉得文章对你有帮助,别忘了点赞和转发,予人玫瑰,手有余香😄
需要源码的,可以移步至“超平的编程课”gzh。
相关文章:

堆放砖块-第12届蓝桥杯选拔赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第47讲。 堆放砖块…...
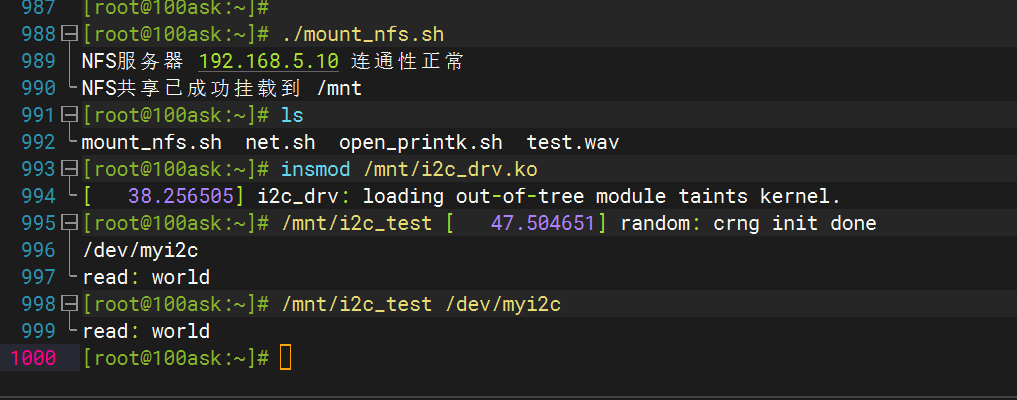
019——IIC模块驱动开发(基于EEPROM【AT24C02】和I.MX6uLL)
目录 一、 IIC基础知识 二、Linux中的IIC(韦东山老师的学习笔记) 1. I2C驱动程序的层次 2. I2C总线-设备-驱动模型 2.1 i2c_driver 2.2 i2c_client 三、 AT24C02 介绍 四、 AT24C02驱动开发 实验 驱动程序 应用程序 一、 IIC基础知识 总线类…...
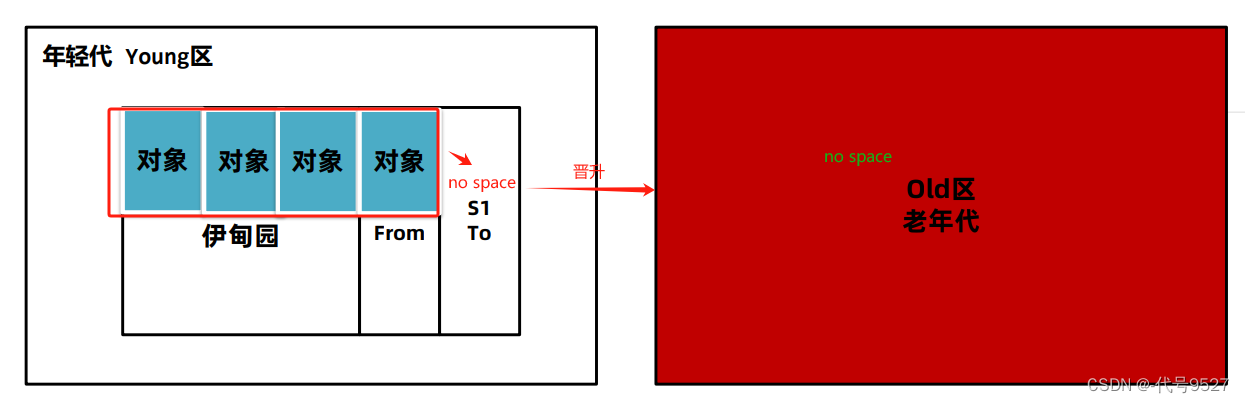
【开发篇】十三、JVM基础参数设置与垃圾回收器的选择
文章目录 1、-Xmx 和 –Xms2、-XX:MaxMetaspaceSize 和 –XX:MetaspaceSize3、-Xss4、不建议改的参数5、其他参数6、选择GC回收器的调试思路7、CMS的并发模式失败现象的解决8、调优案例 GC问题解决方式: 优化JVM基础参数,避免频繁Full GC减少对象的产生…...
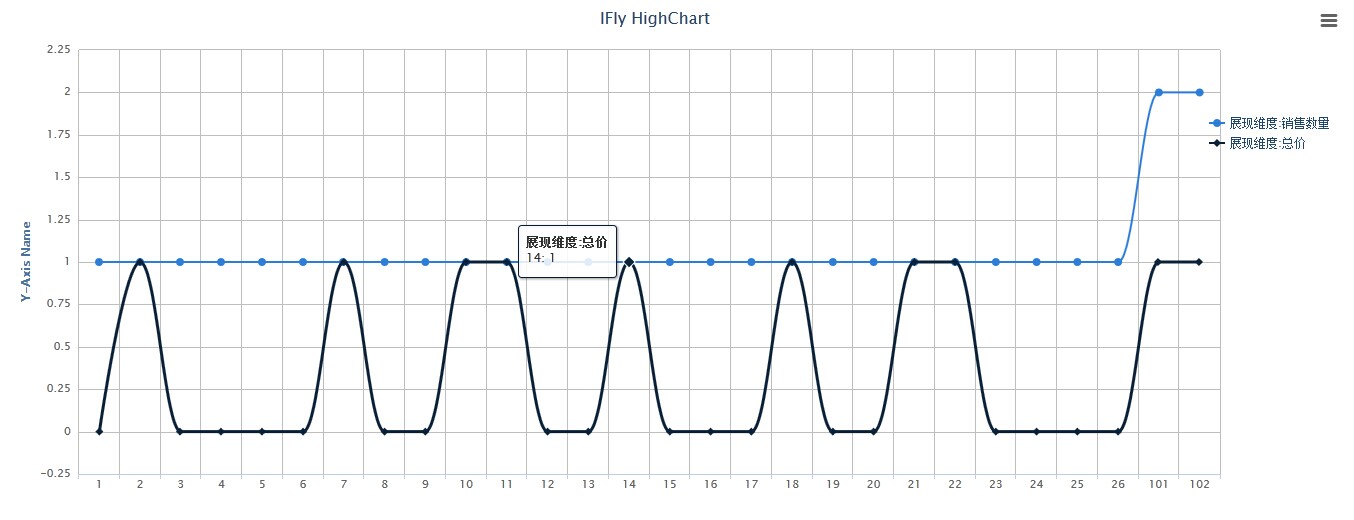
多维 HighCharts
1:showHighChart.html <!DOCTYPE html> <html lang"zh-CN"><head><meta charset"UTF-8"><!-- js脚本都是官方的,后两个是highchart脚本 --><script type"text/javascript" src"jquery1.7.1.mi…...

单细胞RNA测序(scRNA-seq)cellranger count的细胞定量和aggr整合
单细胞RNA测序(scRNA-seq)基础知识可查看以下文章: 单细胞RNA测序(scRNA-seq)工作流程入门 单细胞RNA测序(scRNA-seq)细胞分离与扩增 单细胞RNA测序(scRNA-seq)SRA数据下载及fastq-dumq数据拆分 单细胞RNA测序(scRNA-seq)Cellranger流程入门和数据质控 细胞定量…...

Unity URP 2021 Release-Notes
🌈Unity URP 2021 Release-Notes 本文信息收集来自自动搜集工具👈 版本更新内容2021.3.32URP: Vulkan URP will use MSAA samples count fallback from player settings. Prior to this x2 fallback would have been to upgrade to x4.(UUM-741)2021.3.…...
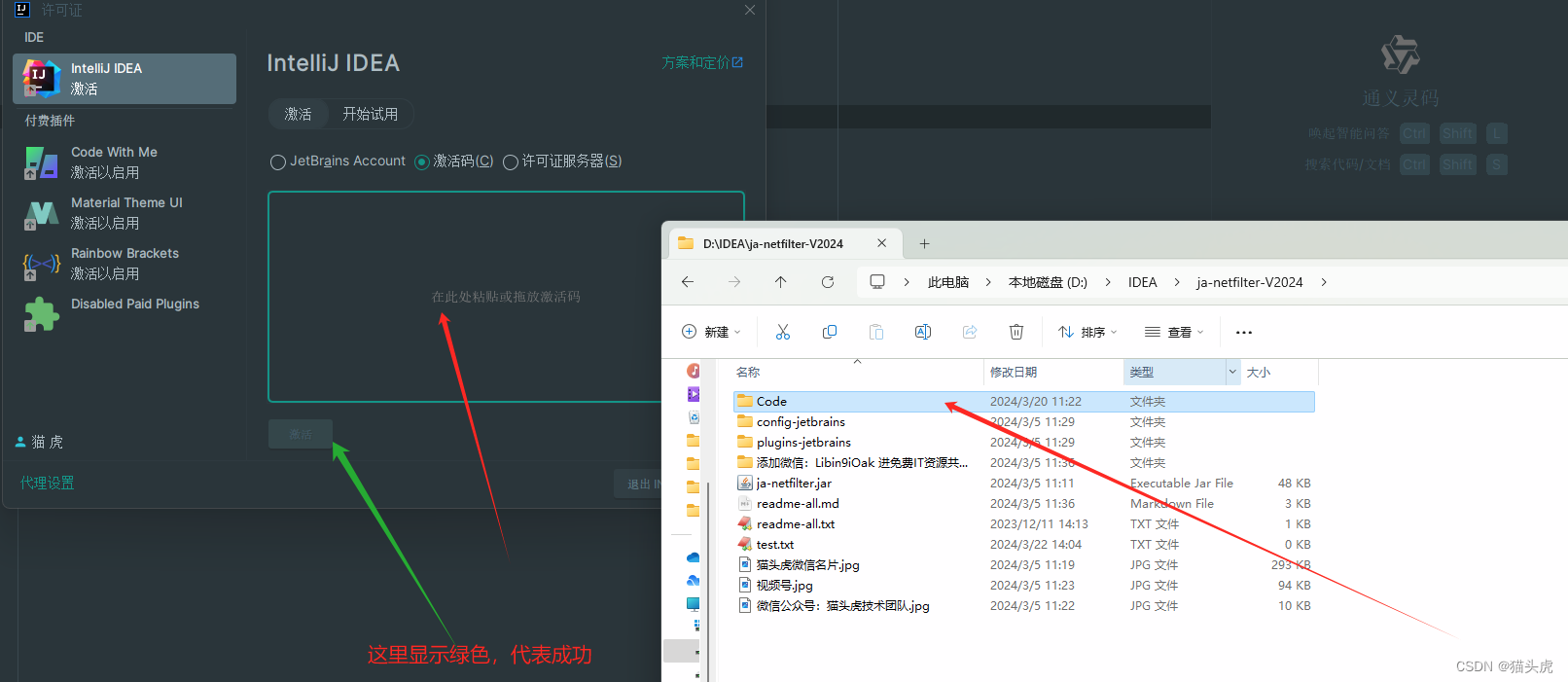
最新IntelliJ IDEA 2024.1 安装和快速配置教程
IntelliJ IDEA 2024.1 最新版如何快速入门体验?IntelliJ IDEA 2024.1 安装和配置教程 图文解说版 文章目录 IntelliJ IDEA 2024.1 最新版如何快速入门体验?IntelliJ IDEA 2024.1 安装和配置教程 图文解说版前言 第一步: IntelliJ IDEA 2024.1安装教程第 0 步&…...

24应届生求职中QAQ
有没有大佬给个机会帮忙内推一下啊,找工作太难了QAQ。 最近一直在BOOS上找工作,但是结果不太理想,一直没有找到满意的工作,有没有大佬帮忙内推一下,有的话请私信我QAQ。...

centos7离线安装postgresql13
**一.**安装存储库RPM yum install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-7-x86_64/pgdg-redhat-repo-latest.noarch.rpm二.使用yumdownloader下载安装包 mkdir pg_yum cd pg_yum yumdownloader --resolve postgresql13-server**三.**上传rpm包到安…...
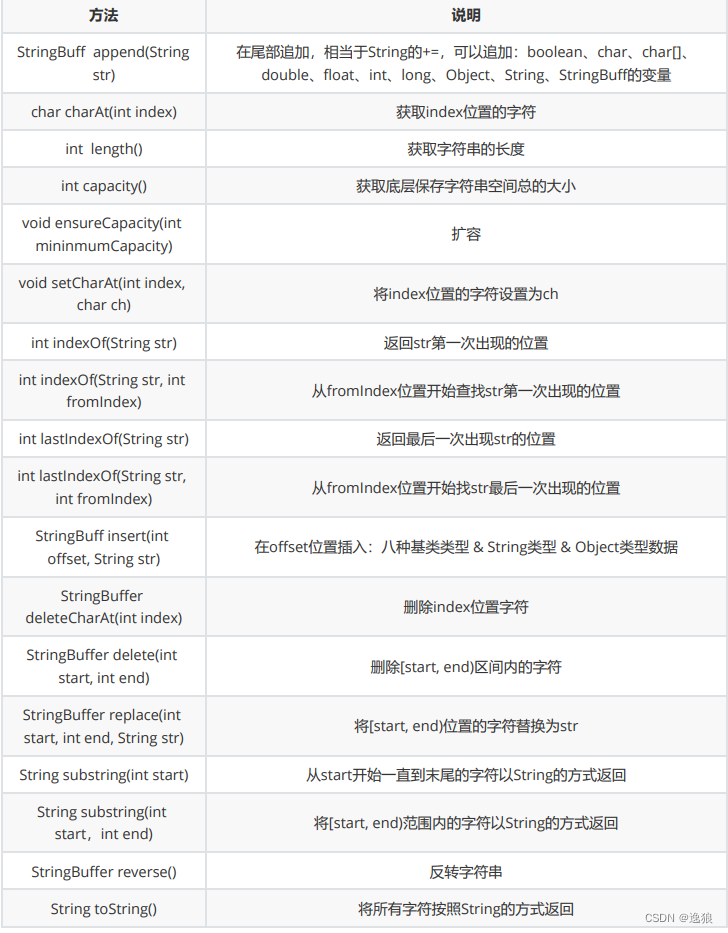
【JavaSE】搞定String类
前言 本篇会细致讲解String类的常见用法,让小伙伴们搞定String类~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 目录 前言 常用的三种字符串构造 字符串长度length 字符串比较 比较 比较字符串的内容equals…...

数字乡村创新实践探索农业现代化与农村治理现代化新路径:科技赋能农村全面振兴与农民幸福生活
目录 引言 一、数字乡村与农业现代化 1、智慧农业技术的应用 2、农业产业链的数字化转型 二、数字乡村与农村治理现代化 1、农村信息化水平的提升 2、农村治理模式的创新 三、科技赋能农村全面振兴与农民幸福生活 1、提升农业生产效益与农民收入 2、促进农村产业结构…...

【从零开始手搓12306项目】四、12306是如何成为全球最忙碌的网站之一?
4.1 12306有多忙碌 一天的请求量大概1600亿,平均180万/秒(二八理论:20%的事件产生80%的请求),不适合二八理论,因为12306分时间放票 平均一年售出30亿张,高峰期日售票能力达到了2000万张 高峰期…...
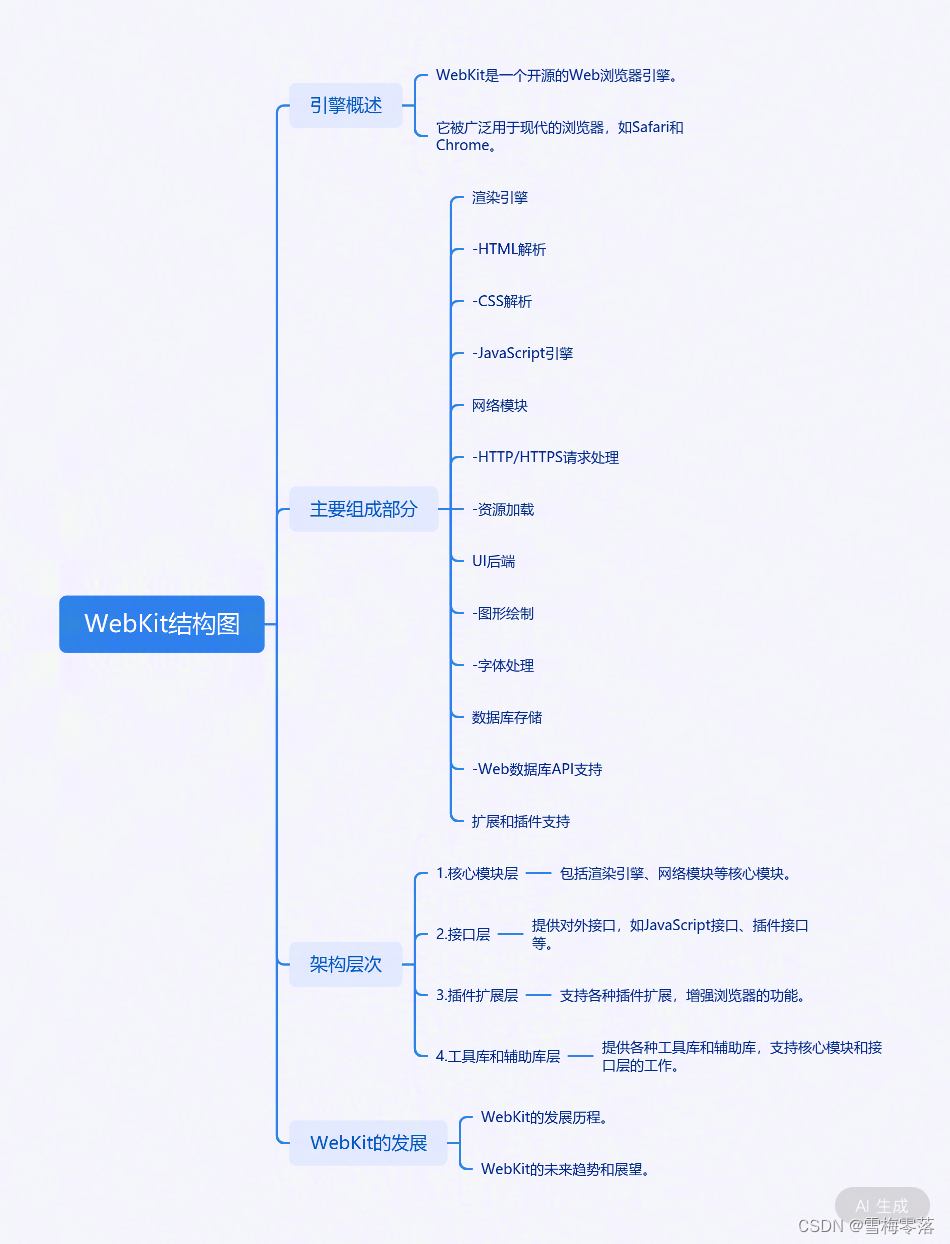
WebKit简介及工作流程
文章目录 一、WebKit简介二、WebKit结构三、Webkit工作流程四、WebKit常见问题五、WebKit优点六、相关链接 一、WebKit简介 WebKit是一个开源的浏览器引擎,它的起源可以追溯到2001年,当时苹果公司推出了其首款基于Unix的操作系统Mac OS X。在2002年&…...

软考-系统集成项目管理中级--进度管理(输入输出很重要!!!本章占分较高,着重复习)
本章历年考题分值统计(16年11月及以后按新教材考的) 本章重点常考知识点汇总清单(学握部分可直接理解记忆) 12、参数估算:参数估算是一种基于历史数据和项目参数,使用某种算法来计算成本或持续时间的估算技术。参数估算是指利用历史数据之间的统计关系和…...

AndroidAutomotive模块介绍(一)整体介绍
前言 Android Automotive 是一个基本 Android 平台,可运行 IVI 系统中预安装的 Android 应用以及可选的第二方和第三方 Android 应用。 本系列文档将会系统的介绍 Android Automotive 的功能、架构、逻辑等。模块逻辑将从 应用api接口、系统服务、底层服务&#x…...
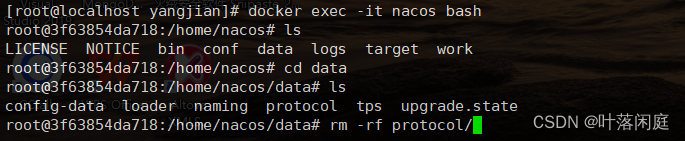
【开发问题记录】Nacos修改服务实例权重时报错
问题记录 一、问题描述1.1 产生原因1.2 产生问题 二、问题解决2.1 docker部署的nacos解决方案2.1.1 进入nacos容器2.1.2 查看当前目录2.1.3 进入data文件夹2.1.4 删除protocol文件2.2 本地部署的nacos 一、问题描述 1.1 产生原因 在运行项目时,在本地启动了一个服务…...

高级IO和5种IO模型
目录 1. 高级IO1.1 IO的基本概念1.2 OS如何得知外设当中有数据可读取1.3 OS如何处理从网卡中读取到的数据包1.4 IO的步骤 2. 五种IO模型2.1 利用钓鱼来理解2.2 阻塞IO2.3 非阻塞IO2.4 信号驱动IO2.5 IO多路转接2.6 异步IO 3. 高级IO的概念3.1 同步通信 VS 异步通信3.2 阻塞 VS …...

OpenHarmony轻量系统开发【7】驱动之I2C显示OLED屏幕
7.1实验效果 Hispark WiFi开发套件又提供一个oled屏幕,但是鸿蒙源码中没有这个屏幕的驱动,我们需要自己去移植。 以下是移植效果: 接口:I2C 使用引脚:HI_IO_NAME_GPIO_13 、 HI_IO_NAME_GPIO_14 7.2代码 这里我直…...

C#:循环中断
任务描述 实现九九乘法表,按照编程要求,使用break跳出循环 测试说明 测试过程: 平台将编译用户补全代码,并根据程序的输出判断程序是否正确。 以下是测试样例: 测试输入: 预期输出: we found…...
34. UE5 RPG实现鼠标点击移动
在前面,我们实现过使用键盘按键wasd去实现控制角色的移动,现在,我们实现了InputAction按键触发,后面,实现一下通过鼠标点击地面实现角色移动。 我们将实现两种效果的切换,如果你点击地面快速松开࿰…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
